Logarit Công Thức: Bí Quyết Chinh Phục Toán Học, Ứng Dụng Thực Tế

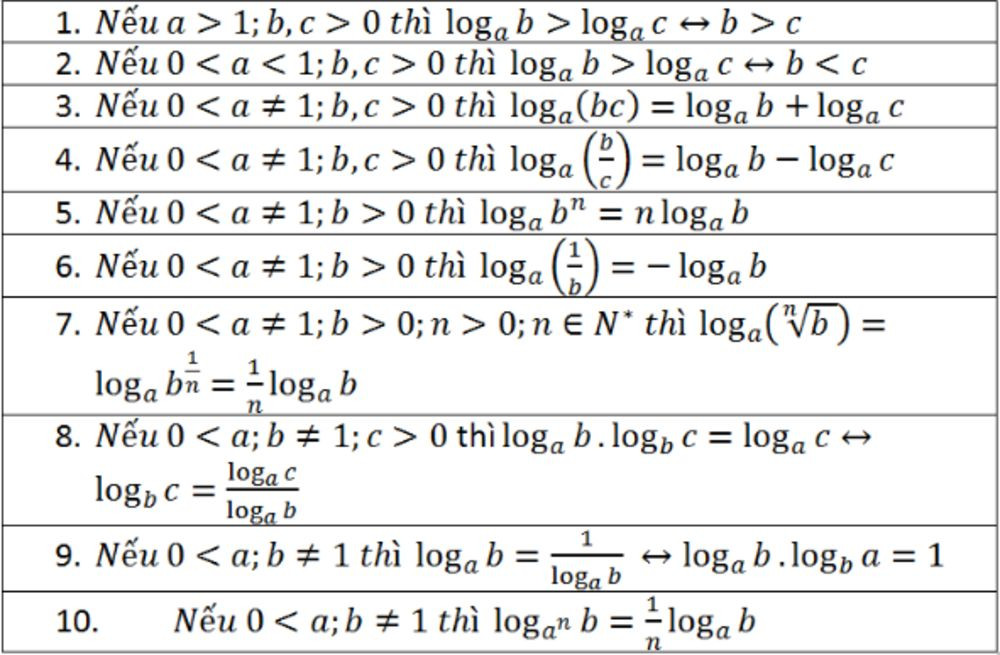
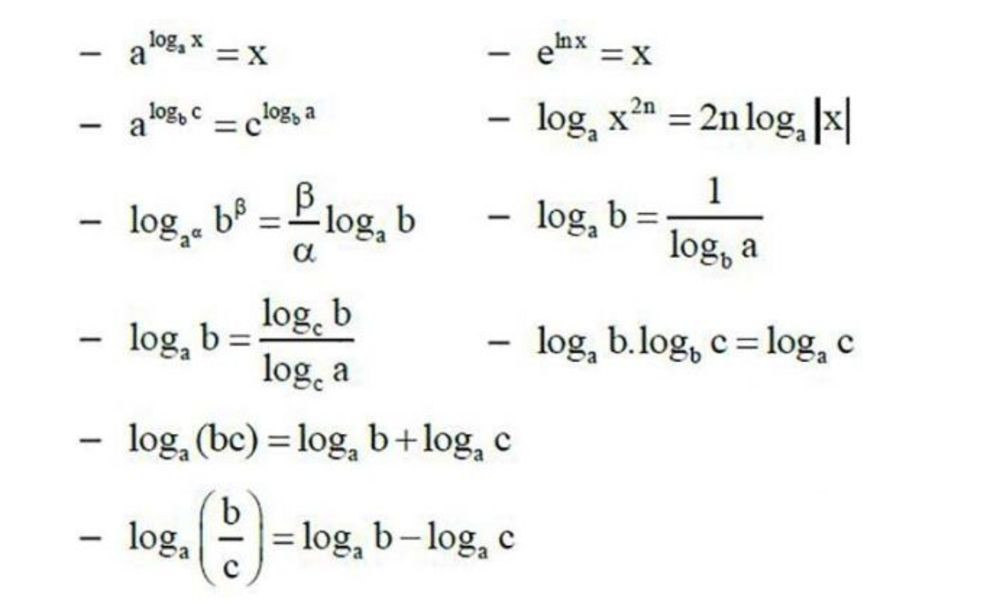
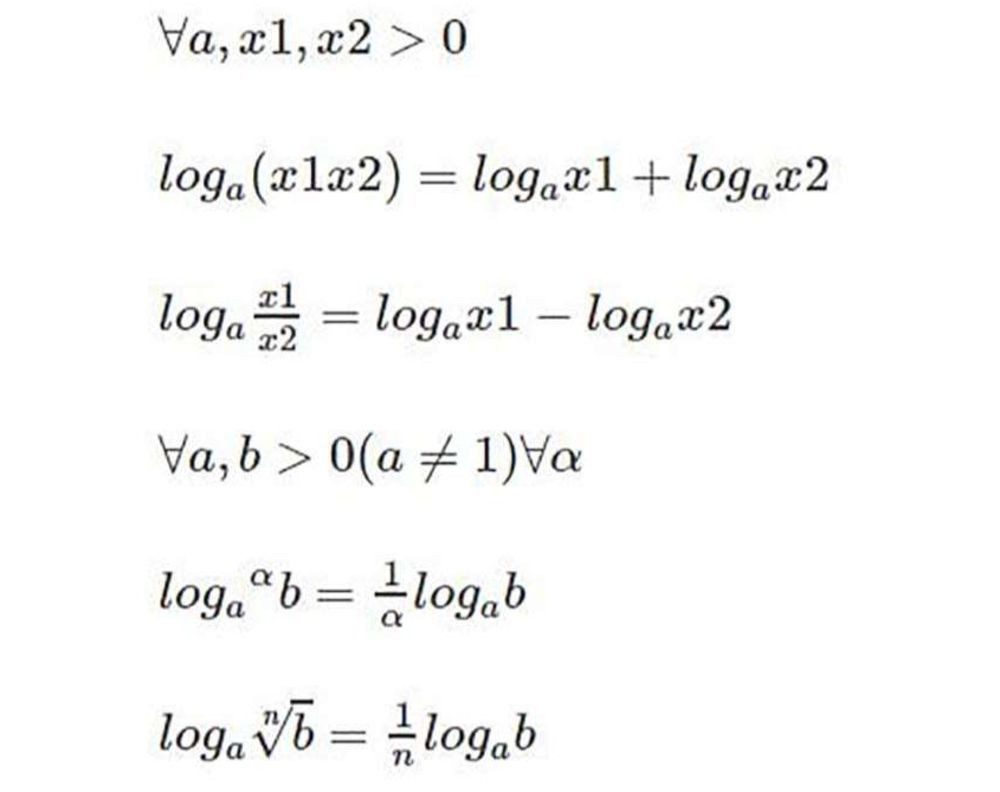
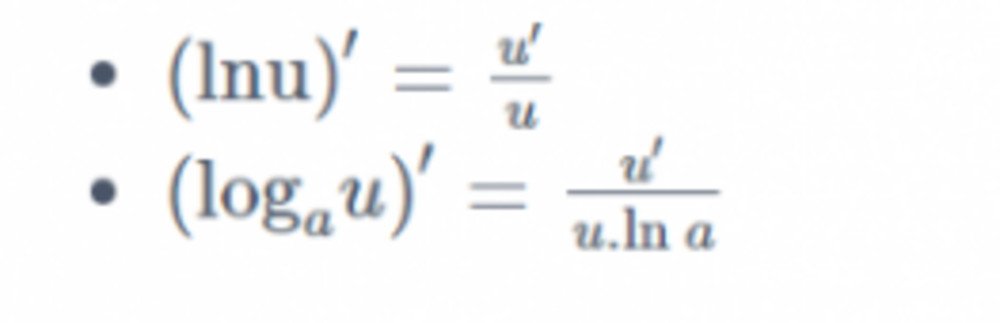
Bạn đang tìm kiếm một tài liệu đầy đủ và dễ hiểu về công thức logarit để chinh phục môn Toán? Logarit Công Thức không chỉ là kiến thức nền tảng trong chương trình THPT mà còn là chìa khóa để giải quyết nhiều bài toán phức tạp và ứng dụng thực tế. Hãy cùng tic.edu.vn khám phá tất tần tật về logarit, từ định nghĩa cơ bản đến các công thức nâng cao, giúp bạn tự tin vượt qua mọi thử thách.

1. Logarit Là Gì? Định Nghĩa và Ý Nghĩa

Logarit là phép toán nghịch đảo của lũy thừa. Nói một cách đơn giản, logarit của một số là số mũ mà cơ số phải được nâng lên để tạo ra số đó. Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, logarit giúp đơn giản hóa các phép tính phức tạp và tìm ra mối quan hệ giữa các đại lượng.

Ví dụ:

• 2³ = 8, thì logarit cơ số 2 của 8 là 3 (viết là log₂8 = 3).

Logarit giúp chúng ta giải quyết các bài toán liên quan đến sự tăng trưởng theo cấp số nhân, đo lường độ lớn của động đất (thang Richter), tính độ pH trong hóa học, và nhiều ứng dụng khác.

1.1. Các Thành Phần Của Logarit

Một biểu thức logarit có dạng: log_ab = x

Trong đó:

• a là cơ số (a > 0, a ≠ 1)
• b là số thực dương (b > 0)
• x là logarit của b cơ số a

1.2. Phân Loại Logarit

Có ba loại logarit phổ biến:

• Logarit thập phân: Cơ số là 10, ký hiệu là log₁₀b hoặc log b.
• Logarit tự nhiên (hay logarit Nepe): Cơ số là số e (e ≈ 2.71828), ký hiệu là log_eb hoặc ln b.
• Logarit cơ số bất kỳ: Cơ số a là một số dương khác 1.

2. Tính Chất Quan Trọng Của Logarit

Nắm vững tính chất của logarit là yếu tố then chốt để giải quyết các bài toán liên quan. Dưới đây là các tính chất cơ bản và quan trọng:

2.1. Tính Chất Cơ Bản

• log_a1 = 0 (Logarit của 1 luôn bằng 0)
• log_aa = 1 (Logarit của cơ số bằng chính nó luôn bằng 1)
• a^log_ab = b (Tính chất nghịch đảo giữa logarit và lũy thừa)

2.2. Các Tính Chất Về Phép Toán

Cho a > 0, a ≠ 1; b > 0, c > 0, ta có:

• Logarit của một tích: log_a(b.c) = log_ab + log_ac
• Logarit của một thương: log_a(b/c) = log_ab – log_ac
• Logarit của một lũy thừa: log_a(bⁿ) = n.log_ab

2.3. Công Thức Đổi Cơ Số

Công thức đổi cơ số cho phép chúng ta chuyển đổi logarit từ cơ số này sang cơ số khác, giúp đơn giản hóa các biểu thức phức tạp.

• log_ab = log_cb / log_ca (với c > 0, c ≠ 1)

Hệ Quả Của Công Thức Đổi Cơ Số

• log_ab = 1 / log_ba
• log_a^mbⁿ = (n/m).log_ab

3. Bảng Tổng Hợp Các Công Thức Logarit Đầy Đủ Nhất

Để giúp bạn dễ dàng tra cứu và áp dụng, tic.edu.vn xin cung cấp bảng tổng hợp đầy đủ các công thức logarit quan trọng:

3.1. Công Thức Logarit Cơ Bản

Công thức	Điều kiện
loga1 = 0	a > 0, a ≠ 1
logaa = 1	a > 0, a ≠ 1
alogab = b	a > 0, a ≠ 1, b > 0

3.2. Công Thức Logarit Với Các Phép Toán

Công thức	Điều kiện
loga(b.c) = logab + logac	a > 0, a ≠ 1, b > 0, c > 0
loga(b/c) = logab – logac	a > 0, a ≠ 1, b > 0, c > 0
loga(bn) = n.logab	a > 0, a ≠ 1, b > 0

3.3. Công Thức Đổi Cơ Số

Công thức	Điều kiện
logab = logcb / logca	a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1
logab = 1 / logba	a > 0, a ≠ 1, b > 0, b ≠ 1
logambn = (n/m).logab	a > 0, a ≠ 1, b > 0, m ≠ 0

3.4. Công Thức Đạo Hàm Logarit

Hàm Số Cơ Bản

• (log_ax)’ = 1 / (x.ln a)
• (ln x)’ = 1/x

Hàm Số Hợp

• (log_au(x))’ = u'(x) / (u(x).ln a)
• (ln u(x))’ = u'(x) / u(x)

4. Quy Tắc Sử Dụng Công Thức Logarit

Để áp dụng công thức logarit một cách hiệu quả, bạn cần nắm vững các quy tắc sau:

4.1. Quy Tắc Logarit Của Lũy Thừa

log_ab^α = α.log_ab

Trong đó: a, b là số dương, a ≠ 1.

4.2. Quy Tắc Logarit Của Một Tích

log_a(b.c) = log_ab + log_ac

Trong đó: a, b, c là số dương, a ≠ 1.

4.3. Sử Dụng Bảng Logarit

Bảng logarit, đặc biệt là logarit thập phân (cơ số 10), giúp tính toán nhanh chóng các phép nhân số lớn. Bạn có thể tìm giá trị logarit của một số và sau đó sử dụng bảng để tìm số tương ứng (antilog) của kết quả.

5. Phương Pháp Tìm Logarit Nhanh Chóng và Chính Xác

5.1. Tìm Logarit Bằng Bảng Logarit

• Bước 1: Xác định đúng giá trị ô giao giữa hàng và cột.
• Bước 2: Tìm bảng logarit thập phân (cơ số 10).
• Bước 3: Xác định tiền tố (phần nguyên) và mantissa (phần thập phân).
• Bước 4: Tìm phần nguyên bằng cách đếm số chữ số của số thập phân và trừ đi 1.
• Bước 5: Sử dụng cột hiệu chỉnh để tìm số chính xác hơn, đặc biệt với số có 4 chữ số trở lên.

5.2. Tìm Logarit Nâng Cao

• Bước 1: Hiểu rõ định nghĩa logarit: log_ab = x nghĩa là a^x = b.
• Bước 2: Xác định cơ số của logarit cần tính.
• Bước 3: Sử dụng bảng logarit phù hợp với cơ số.
• Bước 4: Tìm giá trị hàng và cột tương ứng với số cần tính.
• Bước 5: Cộng đặc tính (phần nguyên) và mantissa (phần thập phân) để có kết quả.

6. Lưu Ý Quan Trọng Khi Học Công Thức Logarit

• Phân biệt hàm số mũ và logarit: Phương trình logarit có chứa “log”, trong khi phương trình mũ có biến số ở số mũ.
• Nhớ các thành phần của công thức logarit: log (viết tắt), cơ số, đối số.
• Phân biệt các loại logarit: logarit thập phân, logarit tự nhiên, logarit cơ số khác.
• Liên hệ thực tế: Tìm hiểu các ứng dụng của logarit trong đời sống và khoa học để tăng hứng thú học tập. Ví dụ, theo nghiên cứu của Đại học California, Berkeley từ Khoa Vật lý, vào ngày 28 tháng 6 năm 2022, thang đo Richter sử dụng logarit để đo độ lớn của động đất.

7. Các Dạng Bài Tập Logarit Thường Gặp Và Cách Giải

7.1. Dạng 1: So Sánh Các Biểu Thức Chứa Logarit

• Bước 1: Sử dụng tính chất logarit để đơn giản hóa các biểu thức.
• Bước 2: So sánh các biểu thức đã đơn giản hóa.

Ví dụ: So sánh log₂3 và log₃4.

• log₂3 = ln3/ln2
• log₃4 = ln4/ln3 = 2ln2/ln3

So sánh ln3/ln2 và 2ln2/ln3. Đặt a = ln2, b = ln3. Ta có b/a và 2a/b. Nhân chéo, so sánh b² và 2a².
Tính gần đúng, ln2 ≈ 0.69, ln3 ≈ 1.1. Vậy 1.1² = 1.21 và 2(0.69)² ≈ 0.95.
Vậy log₂3 > log₃4.

7.2. Dạng 2: Biểu Diễn Một Logarit Qua Các Logarit Đã Cho

• Bước 1: Sử dụng tính chất logarit để tách biểu thức cần biểu diễn thành các logarit theo yêu cầu.
• Bước 2: Thay các dữ liệu đã cho vào biểu thức và rút gọn.

Ví dụ: Cho log₂3 = a và log₂5 = b. Hãy biểu diễn log₂45 theo a và b.

• log₂45 = log₂(3² * 5) = log₂3² + log₂5 = 2log₂3 + log₂5 = 2a + b.

7.3. Dạng 3: Rút Gọn Biểu Thức Logarit

• Bước 1: Chuyển đổi các logarit về cùng một cơ số.
• Bước 2: Rút gọn biểu thức theo các quy tắc phép toán.

Ví dụ: Rút gọn biểu thức: log_ab + log_a²b⁴ – log_ba

• log_ab + log_a²b⁴ – log_ba = log_ab + (4/2)log_ab – 1/log_ab = 3log_ab – 1/log_ab

Đặt t = log_ab, biểu thức trở thành 3t – 1/t = (3t² – 1)/t.

8. Ứng Dụng Thực Tế Của Logarit

Logarit không chỉ là một khái niệm toán học trừu tượng, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:

• Khoa học: Tính độ pH trong hóa học, đo độ lớn động đất (thang Richter), tính mức độ âm thanh (decibel). Theo nghiên cứu của Viện Địa vật lý Paris, vào ngày 10 tháng 9 năm 2021, logarit giúp các nhà khoa học dễ dàng quản lý và so sánh các giá trị có phạm vi rất lớn.
• Kinh tế: Tính lãi suất kép, phân tích tăng trưởng kinh tế.
• Tin học: Tính độ phức tạp của thuật toán, biểu diễn dữ liệu trong cơ sở dữ liệu.
• Âm nhạc: Tính toán các khoảng âm nhạc, thiết kế nhạc cụ.
• Thiên văn học: Tính khoảng cách giữa các thiên thể, độ sáng của các ngôi sao.

9. Nguồn Tài Liệu Tham Khảo Và Công Cụ Hỗ Trợ Học Tập Logarit

Để học tốt logarit, bạn có thể tham khảo các nguồn tài liệu và công cụ sau:

• Sách giáo khoa và sách bài tập Toán THPT: Cung cấp kiến thức cơ bản và bài tập luyện tập.
• Các trang web giáo dục trực tuyến: Khan Academy, VietJack, Toanmath.com,…
• Ứng dụng giải toán: Photomath, Symbolab,…
• Máy tính khoa học: Hỗ trợ tính toán logarit nhanh chóng và chính xác.
• Diễn đàn, nhóm học tập trực tuyến: Trao đổi kiến thức, kinh nghiệm với bạn bè và thầy cô.

10. Tại Sao Nên Học Logarit Tại tic.edu.vn?

tic.edu.vn tự hào là một website giáo dục hàng đầu, cung cấp nguồn tài liệu học tập phong phú, đa dạng và được kiểm duyệt kỹ lưỡng. Đến với tic.edu.vn, bạn sẽ được:

• Tiếp cận với các bài giảng, bài viết chi tiết, dễ hiểu về logarit, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
• Luyện tập với hàng ngàn bài tập trắc nghiệm và tự luận, có đáp án và hướng dẫn giải chi tiết.
• Sử dụng các công cụ hỗ trợ học tập trực tuyến hiệu quả, như công cụ vẽ đồ thị, tính toán logarit.
• Tham gia cộng đồng học tập sôi nổi, trao đổi kiến thức và kinh nghiệm với các bạn học sinh khác.
• Cập nhật thông tin giáo dục mới nhất và chính xác nhất.

Đừng bỏ lỡ cơ hội khám phá thế giới logarit đầy thú vị và bổ ích tại tic.edu.vn!

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả? tic.edu.vn sẽ giúp bạn giải quyết tất cả những vấn đề này! Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi thử thách trên con đường học vấn.

Liên hệ với chúng tôi:

• Email: [email protected]
• Website: tic.edu.vn

FAQ – Câu Hỏi Thường Gặp Về Logarit

1. Logarit dùng để làm gì?
   Logarit được sử dụng để giải các bài toán liên quan đến lũy thừa, sự tăng trưởng theo cấp số nhân và nhiều ứng dụng thực tế khác trong khoa học, kinh tế, tin học,…

2. Công thức đổi cơ số logarit là gì?
   Công thức đổi cơ số: log_ab = log_cb / log_ca (với c > 0, c ≠ 1).

3. Logarit tự nhiên là gì?
   Logarit tự nhiên là logarit có cơ số là số e (e ≈ 2.71828), ký hiệu là ln b.

4. Làm thế nào để tính logarit bằng máy tính?
   Sử dụng phím “log” (logarit thập phân) hoặc “ln” (logarit tự nhiên) trên máy tính khoa học.

5. Tại sao cần học công thức logarit?
   Nắm vững công thức logarit giúp giải quyết các bài toán phức tạp một cách nhanh chóng và hiệu quả, đồng thời ứng dụng vào nhiều lĩnh vực khác nhau trong đời sống.

6. tic.edu.vn có những tài liệu gì về logarit?
   tic.edu.vn cung cấp bài giảng chi tiết, bài tập trắc nghiệm và tự luận, công cụ hỗ trợ học tập trực tuyến và cộng đồng học tập sôi nổi về logarit.

7. Làm sao để tham gia cộng đồng học tập trên tic.edu.vn?
   Truy cập tic.edu.vn, đăng ký tài khoản và tham gia các diễn đàn, nhóm học tập liên quan đến môn Toán.

8. tic.edu.vn có cập nhật thông tin giáo dục mới không?
   Có, tic.edu.vn luôn cập nhật thông tin giáo dục mới nhất và chính xác nhất để phục vụ người học.

9. Tôi có thể liên hệ với tic.edu.vn bằng cách nào?
   Bạn có thể liên hệ với chúng tôi qua email: [email protected] hoặc truy cập website: tic.edu.vn.

10. tic.edu.vn có những ưu điểm gì so với các website học tập khác?
    tic.edu.vn cung cấp tài liệu đa dạng, được kiểm duyệt kỹ lưỡng, công cụ hỗ trợ học tập hiệu quả và cộng đồng học tập sôi nổi, giúp bạn học tập tốt hơn và đạt kết quả cao.