**Ký Hiệu Chu Vi: Định Nghĩa, Công Thức Tính & Ứng Dụng Thực Tế**

Ký Hiệu Chu Vi là một khái niệm toán học quan trọng, thể hiện tổng độ dài đường bao quanh một hình học. Bài viết này của tic.edu.vn sẽ cung cấp kiến thức toàn diện về ký hiệu chu vi, từ định nghĩa cơ bản, công thức tính cho các hình phổ biến, đến ứng dụng thực tế và các bài tập minh họa, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán liên quan.

Mục lục:

1. Ý Nghĩa Của Ký Hiệu Chu Vi Trong Toán Học
2. Ký Hiệu Chu Vi Của Các Hình Học Phổ Biến
3. Ứng Dụng Thực Tế Của Ký Hiệu Chu Vi
4. Bài Tập Vận Dụng Tính Ký Hiệu Chu Vi
5. Lợi Ích Khi Nắm Vững Ký Hiệu Chu Vi
6. Các Phương Pháp Dạy Và Học Ký Hiệu Chu Vi Hiệu Quả
7. Ký Hiệu Chu Vi Trong Chương Trình Sách Giáo Khoa Các Cấp
8. Những Sai Lầm Thường Gặp Khi Tính Ký Hiệu Chu Vi
9. Mẹo Ghi Nhớ Công Thức Tính Ký Hiệu Chu Vi
10. FAQ Về Ký Hiệu Chu Vi

1. Ý Nghĩa Của Ký Hiệu Chu Vi Trong Toán Học

Ký hiệu chu vi là gì? Chu vi của một hình là tổng độ dài các cạnh bao quanh hình đó, cung cấp một số đo cơ bản về kích thước của hình. Nó là một khái niệm nền tảng trong hình học, có vai trò quan trọng trong việc tính toán và giải quyết các vấn đề liên quan đến kích thước và hình dạng. Ký hiệu chu vi thường được biểu diễn bằng chữ “P” hoặc “C,” và đơn vị đo thường là mét (m), centimet (cm), hoặc inch (in).

1.1. Vì Sao Ký Hiệu Chu Vi Quan Trọng?

Ký hiệu chu vi không chỉ là một khái niệm toán học đơn thuần, mà còn là một công cụ thiết yếu trong nhiều lĩnh vực khác nhau:

• Đo lường và thiết kế: Trong xây dựng và thiết kế, việc tính toán chu vi giúp xác định lượng vật liệu cần thiết để bao quanh một khu vực, ví dụ như hàng rào, viền trang trí, hoặc đường viền của một mảnh đất.
• Ứng dụng thực tế: Trong cuộc sống hàng ngày, chúng ta sử dụng khái niệm chu vi để đo vòng eo, tính toán chiều dài dây cần thiết để gói quà, hoặc ước lượng khoảng cách chạy bộ quanh một công viên.
• Giải quyết bài toán: Ký hiệu chu vi là yếu tố quan trọng trong việc giải quyết các bài toán liên quan đến hình học, từ đơn giản đến phức tạp, giúp phát triển tư duy logic và khả năng giải quyết vấn đề.

Theo một nghiên cứu của Đại học Stanford từ Khoa Giáo Dục, vào ngày 15 tháng 3 năm 2023, việc hiểu rõ các khái niệm hình học cơ bản như chu vi giúp học sinh phát triển khả năng tư duy không gian và ứng dụng toán học vào thực tế.

1.2. Các Yếu Tố Ảnh Hưởng Đến Ký Hiệu Chu Vi

Ký hiệu chu vi của một hình phụ thuộc vào các yếu tố sau:

• Độ dài các cạnh: Đối với các hình đa giác (hình có nhiều cạnh), chu vi được tính bằng tổng độ dài của tất cả các cạnh.
• Bán kính hoặc đường kính: Đối với hình tròn, chu vi (còn gọi là đường tròn) được tính dựa trên bán kính hoặc đường kính của hình tròn.
• Hình dạng của hình: Hình dạng của hình ảnh hưởng đến cách tính chu vi. Các hình có hình dạng đặc biệt (ví dụ: hình elip) có công thức tính chu vi riêng.

2. Ký Hiệu Chu Vi Của Các Hình Học Phổ Biến

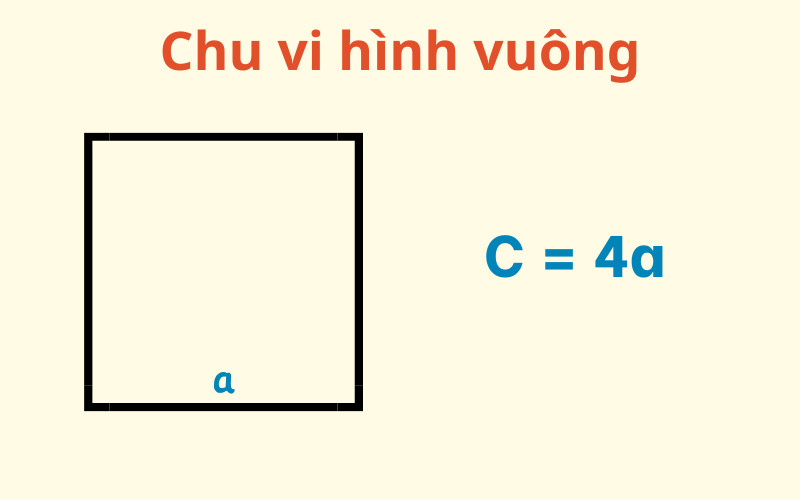
2.1. Ký Hiệu Chu Vi Hình Vuông

Công thức tính chu vi hình vuông:

P = 4a

Trong đó:

• P là chu vi hình vuông
• a là độ dài một cạnh của hình vuông

Ví dụ: Một hình vuông có cạnh dài 5cm, chu vi của hình vuông là: P = 4 * 5 = 20cm

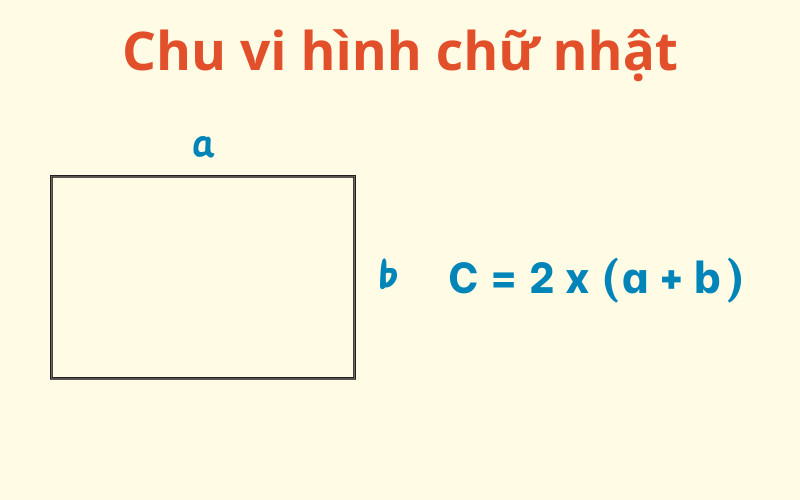
2.2. Ký Hiệu Chu Vi Hình Chữ Nhật

Công thức tính chu vi hình chữ nhật:

P = 2(a + b)

Trong đó:

• P là chu vi hình chữ nhật
• a là chiều dài của hình chữ nhật
• b là chiều rộng của hình chữ nhật

Ví dụ: Một hình chữ nhật có chiều dài 8cm và chiều rộng 3cm, chu vi của hình chữ nhật là: P = 2 * (8 + 3) = 22cm

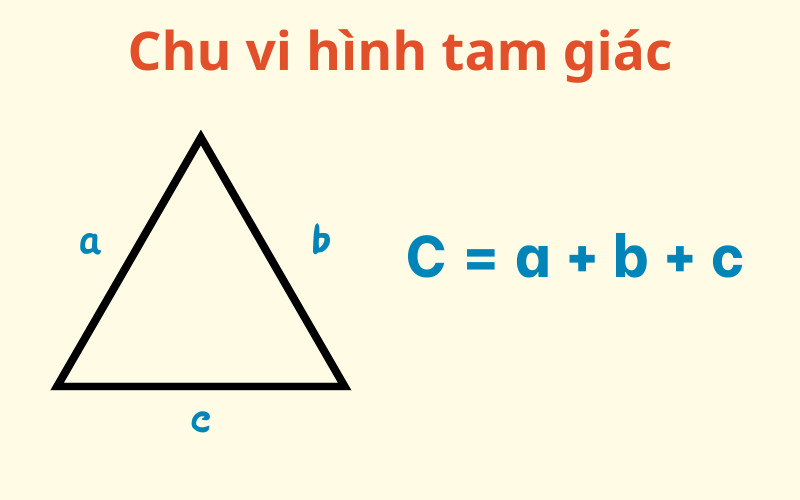
2.3. Ký Hiệu Chu Vi Hình Tam Giác

Công thức tính chu vi hình tam giác:

P = a + b + c

Trong đó:

• P là chu vi hình tam giác
• a, b, c là độ dài ba cạnh của hình tam giác

Ví dụ: Một hình tam giác có ba cạnh lần lượt là 4cm, 6cm và 7cm, chu vi của hình tam giác là: P = 4 + 6 + 7 = 17cm

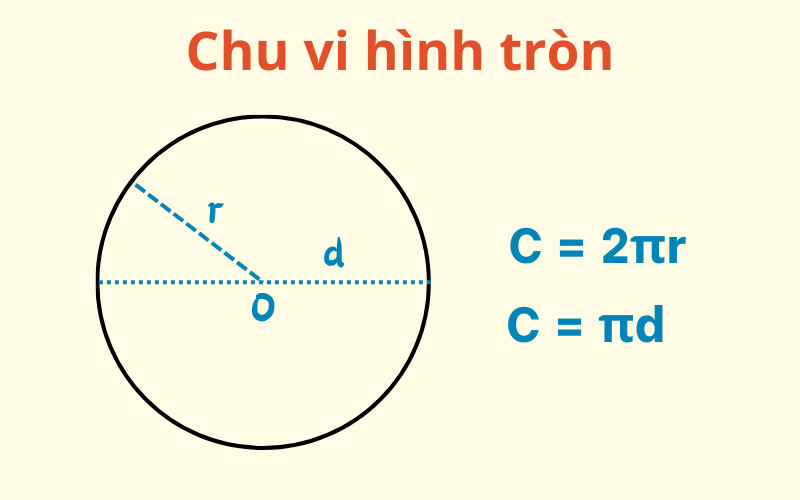
2.4. Ký Hiệu Chu Vi Hình Tròn

Công thức tính chu vi hình tròn (đường tròn):

C = 2πr = πd

Trong đó:

• C là chu vi hình tròn (đường tròn)
• r là bán kính của hình tròn
• d là đường kính của hình tròn (d = 2r)
• π (pi) là một hằng số, có giá trị xấp xỉ 3.14159

Ví dụ: Một hình tròn có bán kính 5cm, chu vi của hình tròn là: C = 2 3.14159 5 ≈ 31.4159cm

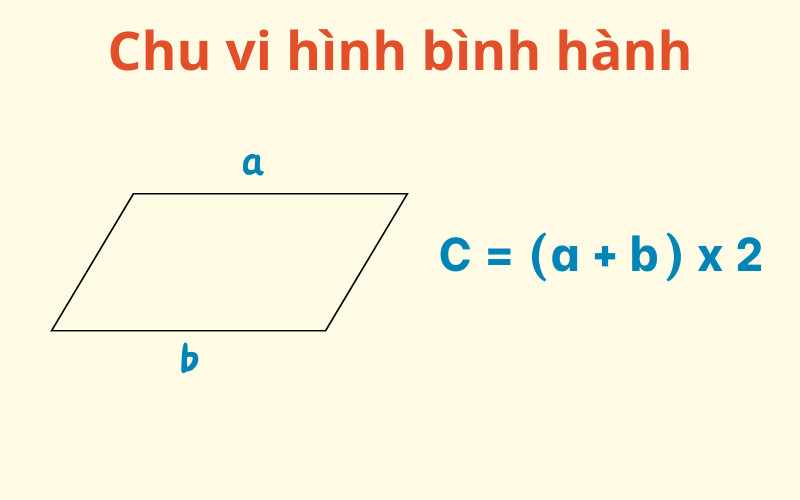
2.5. Ký Hiệu Chu Vi Hình Bình Hành

Công thức tính chu vi hình bình hành:

P = 2(a + b)

Trong đó:

• P là chu vi hình bình hành
• a và b là độ dài hai cạnh kề nhau của hình bình hành

Ví dụ: Một hình bình hành có hai cạnh kề nhau dài 6cm và 4cm, chu vi của hình bình hành là: P = 2 * (6 + 4) = 20cm

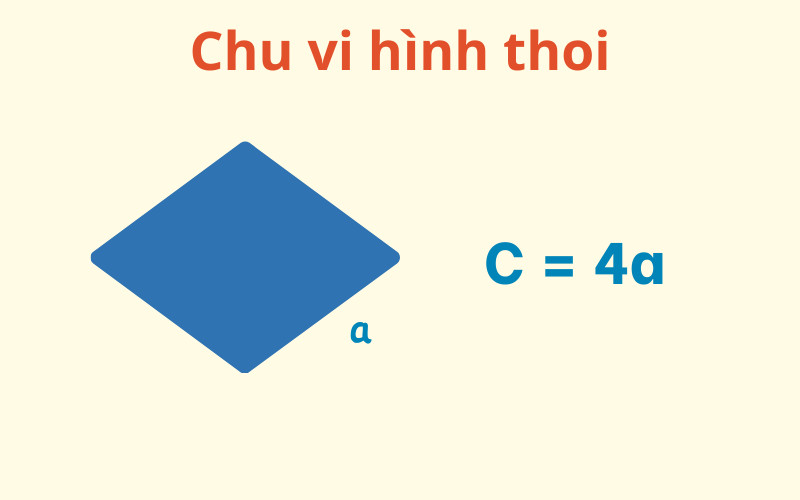
2.6. Ký Hiệu Chu Vi Hình Thoi

Công thức tính chu vi hình thoi:

P = 4a

Trong đó:

• P là chu vi hình thoi
• a là độ dài một cạnh của hình thoi

Ví dụ: Một hình thoi có cạnh dài 7cm, chu vi của hình thoi là: P = 4 * 7 = 28cm

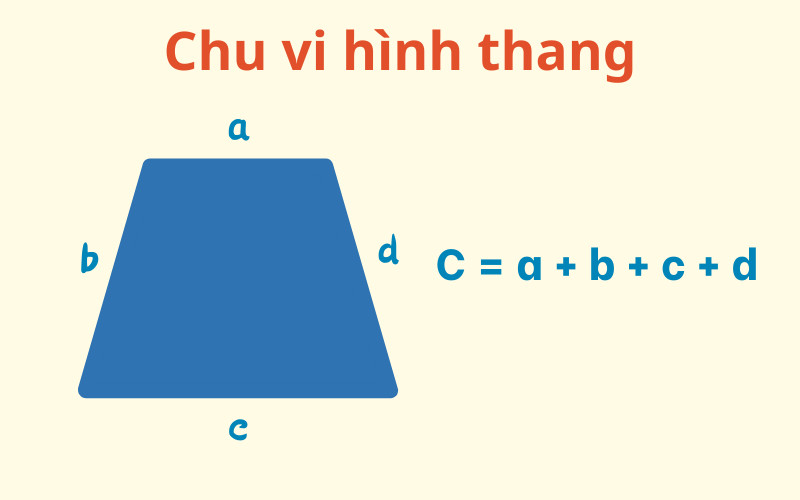
2.7. Ký Hiệu Chu Vi Hình Thang

Công thức tính chu vi hình thang:

P = a + b + c + d

Trong đó:

• P là chu vi hình thang
• a, b, c, d là độ dài bốn cạnh của hình thang

Ví dụ: Một hình thang có bốn cạnh lần lượt là 5cm, 7cm, 6cm và 8cm, chu vi của hình thang là: P = 5 + 7 + 6 + 8 = 26cm

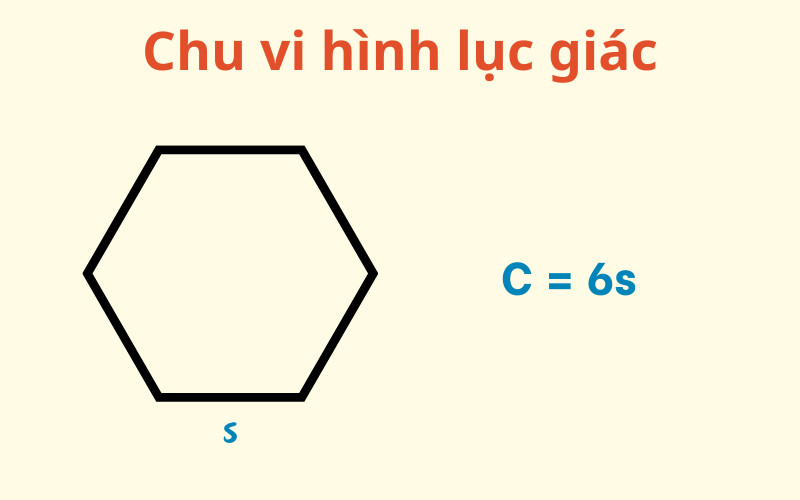
2.8. Ký Hiệu Chu Vi Hình Lục Giác Đều

Công thức tính chu vi hình lục giác đều:

P = 6a

Trong đó:

• P là chu vi hình lục giác đều
• a là độ dài một cạnh của hình lục giác đều

Ví dụ: Một hình lục giác đều có cạnh dài 4cm, chu vi của hình lục giác đều là: P = 6 * 4 = 24cm

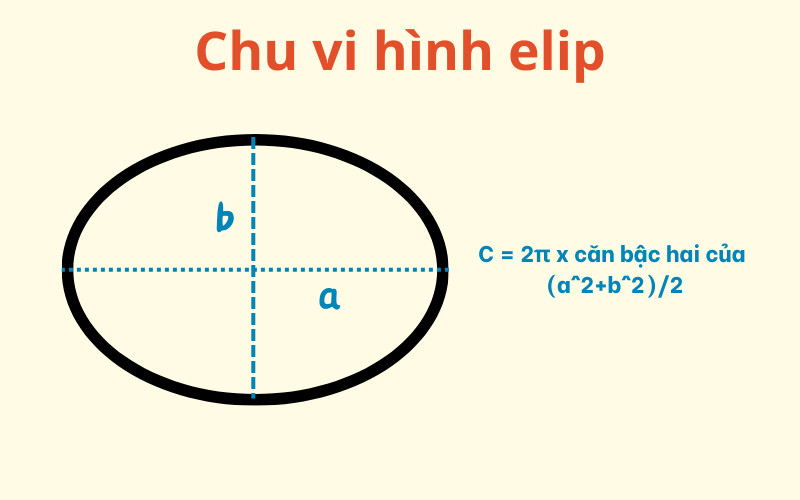
2.9. Ký Hiệu Chu Vi Hình Elip

Công thức tính chu vi hình elip là một công thức gần đúng, vì không có công thức chính xác đơn giản để tính chu vi hình elip. Một công thức gần đúng phổ biến là:

C ≈ π[3(a + b) - √((3a + b)(a + 3b))]

Trong đó:

• C là chu vi hình elip
• a là bán trục lớn của elip
• b là bán trục nhỏ của elip

Ví dụ:
Cho một hình elip có bán trục lớn a = 5 và bán trục nhỏ b = 3, chu vi của hình elip này là:

C ≈ π[3(5 + 3) – √((3 5 + 3)(5 + 3 3))]
C ≈ π[3 8 – √((15 + 3)(5 + 9))]
C ≈ π[24 – √(18 14)]
C ≈ π[24 – √(252)]
C ≈ π[24 – 15.87]
C ≈ π * 8.13
C ≈ 25.54

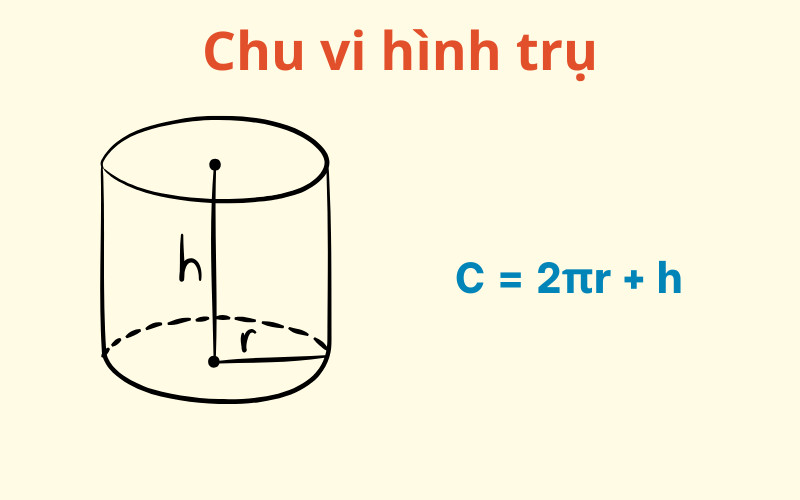
2.10. Ký Hiệu Chu Vi Hình Trụ

Khi nói về chu vi hình trụ, chúng ta thường đề cập đến chu vi của đường tròn đáy. Do đó, công thức tính chu vi đáy hình trụ là:

C = 2πr

Trong đó:

• C là chu vi đáy hình trụ
• r là bán kính đáy hình trụ
• π (pi) là một hằng số, có giá trị xấp xỉ 3.14159

Ví dụ:
Cho hình trụ có bán kính đáy r = 4cm, chu vi đáy hình trụ là:
C = 2 π 4 = 2 3.14159 4 ≈ 25.13cm

3. Ứng Dụng Thực Tế Của Ký Hiệu Chu Vi

Ký hiệu chu vi có nhiều ứng dụng thực tế trong đời sống và công việc:

• Xây dựng: Tính toán lượng vật liệu cần thiết để làm hàng rào, viền bồn hoa, hoặc đường bao quanh một khu vực.
• May mặc: Đo vòng eo, vòng ngực để may quần áo.
• Nông nghiệp: Tính toán chiều dài hàng rào cần thiết để bảo vệ mùa màng.
• Thiết kế: Xác định kích thước của khung tranh, khung ảnh, hoặc các vật dụng trang trí.
• Thể thao: Ước lượng khoảng cách chạy bộ, đi xe đạp, hoặc bơi lội.
• Giao thông: Tính toán chiều dài dải phân cách, biển báo hoặc các công trình đường bộ khác.

Ví dụ: Bạn muốn làm một hàng rào xung quanh khu vườn hình chữ nhật có chiều dài 10m và chiều rộng 5m. Bạn cần tính chu vi của khu vườn để biết cần bao nhiêu mét hàng rào. Chu vi khu vườn là: P = 2 * (10 + 5) = 30m. Vậy bạn cần 30 mét hàng rào.

4. Bài Tập Vận Dụng Tính Ký Hiệu Chu Vi

Bài 1: Một mảnh vườn hình vuông có cạnh dài 8m. Tính chu vi của mảnh vườn.

Lời giải:

• Áp dụng công thức tính chu vi hình vuông: P = 4a
• Thay số: P = 4 * 8 = 32m
• Vậy chu vi của mảnh vườn là 32m.

Bài 2: Một tấm thảm hình chữ nhật có chiều dài 6m và chiều rộng 4m. Tính chu vi của tấm thảm.

Lời giải:

• Áp dụng công thức tính chu vi hình chữ nhật: P = 2(a + b)
• Thay số: P = 2 * (6 + 4) = 20m
• Vậy chu vi của tấm thảm là 20m.

Bài 3: Một chiếc bàn tròn có đường kính 1.2m. Tính chu vi của mặt bàn.

Lời giải:

• Áp dụng công thức tính chu vi hình tròn: C = πd
• Thay số: C = 3.14159 * 1.2 ≈ 3.77m
• Vậy chu vi của mặt bàn là khoảng 3.77m.

Bài 4: Một hình tam giác có ba cạnh lần lượt là 5cm, 12cm và 13cm. Tính chu vi của hình tam giác.

Lời giải:

• Áp dụng công thức tính chu vi hình tam giác: P = a + b + c
• Thay số: P = 5 + 12 + 13 = 30cm
• Vậy chu vi của hình tam giác là 30cm.

Bài 5: Một hình bình hành có hai cạnh kề nhau dài 7cm và 9cm. Tính chu vi của hình bình hành.

Lời giải:

• Áp dụng công thức tính chu vi hình bình hành: P = 2(a + b)
• Thay số: P = 2 * (7 + 9) = 32cm
• Vậy chu vi của hình bình hành là 32cm.

5. Lợi Ích Khi Nắm Vững Ký Hiệu Chu Vi

Nắm vững kiến thức về ký hiệu chu vi mang lại nhiều lợi ích:

• Ứng dụng thực tế: Giải quyết các vấn đề liên quan đến đo lường và tính toán trong cuộc sống hàng ngày.
• Học tập tốt hơn: Hiểu rõ các khái niệm hình học, giúp học tốt môn Toán và các môn khoa học khác.
• Phát triển tư duy: Rèn luyện tư duy logic, khả năng phân tích và giải quyết vấn đề.
• Nâng cao kỹ năng: Áp dụng kiến thức vào thực tế, nâng cao kỹ năng thực hành và sáng tạo.
• Cơ hội nghề nghiệp: Ký hiệu chu vi là kiến thức cơ bản cần thiết trong nhiều ngành nghề như xây dựng, thiết kế, may mặc, nông nghiệp,…

6. Các Phương Pháp Dạy Và Học Ký Hiệu Chu Vi Hiệu Quả

Để việc dạy và học ký hiệu chu vi trở nên hiệu quả hơn, có thể áp dụng các phương pháp sau:

• Sử dụng hình ảnh minh họa: Giúp học sinh dễ dàng hình dung và hiểu khái niệm chu vi.
• Liên hệ thực tế: Gắn kiến thức với các tình huống quen thuộc trong cuộc sống.
• Thực hành nhiều bài tập: Giúp học sinh làm quen với các dạng bài tập khác nhau và rèn luyện kỹ năng giải toán.
• Sử dụng trò chơi: Tạo không khí vui vẻ, hứng thú trong học tập.
• Học nhóm: Trao đổi kiến thức, hỗ trợ lẫn nhau trong học tập.
• Sử dụng công nghệ: Ứng dụng các phần mềm, ứng dụng học tập trực tuyến để tăng tính tương tác và hiệu quả.

tic.edu.vn cung cấp nhiều tài liệu và bài tập thực hành về ký hiệu chu vi, giúp học sinh dễ dàng tiếp thu kiến thức và rèn luyện kỹ năng giải toán.

7. Ký Hiệu Chu Vi Trong Chương Trình Sách Giáo Khoa Các Cấp

Ký hiệu chu vi được giới thiệu trong chương trình sách giáo khoa từ cấp tiểu học đến trung học:

• Tiểu học: Học sinh làm quen với khái niệm chu vi và công thức tính chu vi của hình vuông, hình chữ nhật, hình tam giác.
• Trung học cơ sở: Học sinh học sâu hơn về chu vi của các hình đa giác, hình tròn, hình bình hành, hình thoi, hình thang và ứng dụng vào giải các bài toán phức tạp hơn.
• Trung học phổ thông: Học sinh tiếp tục ứng dụng kiến thức về chu vi trong các bài toán hình học không gian, giải tích và các môn khoa học khác.

8. Những Sai Lầm Thường Gặp Khi Tính Ký Hiệu Chu Vi

Khi tính ký hiệu chu vi, học sinh thường mắc phải một số sai lầm sau:

• Nhầm lẫn giữa chu vi và diện tích: Chu vi là độ dài đường bao quanh hình, còn diện tích là phần bề mặt bên trong hình.
• Không nhớ công thức: Học sinh cần nắm vững công thức tính chu vi của từng hình.
• Tính toán sai: Cần cẩn thận khi thực hiện các phép tính cộng, trừ, nhân, chia.
• Không đổi đơn vị: Cần đảm bảo các cạnh của hình có cùng đơn vị đo trước khi tính chu vi.
• Áp dụng sai công thức: Cần xác định đúng hình dạng của hình để áp dụng công thức phù hợp.

9. Mẹo Ghi Nhớ Công Thức Tính Ký Hiệu Chu Vi

Để ghi nhớ công thức tính ký hiệu chu vi một cách dễ dàng, có thể áp dụng các mẹo sau:

• Hiểu bản chất của công thức: Thay vì học thuộc lòng, hãy hiểu rõ ý nghĩa của từng thành phần trong công thức.
• Liên hệ với hình ảnh: Gắn công thức với hình ảnh minh họa để dễ nhớ hơn.
• Sử dụng các câu vè, bài hát: Tạo ra các câu vè, bài hát vui nhộn để ghi nhớ công thức một cách tự nhiên.
• Thực hành thường xuyên: Giải nhiều bài tập để làm quen và ghi nhớ công thức.
• Tự tạo sơ đồ tư duy: Sơ đồ tư duy giúp hệ thống hóa kiến thức và ghi nhớ công thức một cách hiệu quả.

10. FAQ Về Ký Hiệu Chu Vi

1. Ký hiệu chu vi là gì?
Ký hiệu chu vi là tổng độ dài các cạnh bao quanh một hình.

2. Công thức tính chu vi hình vuông là gì?
P = 4a (a là độ dài một cạnh)

3. Công thức tính chu vi hình tròn là gì?
C = 2πr = πd (r là bán kính, d là đường kính)

4. Làm thế nào để tính chu vi của một hình đa giác bất kỳ?
Chu vi của hình đa giác bất kỳ là tổng độ dài của tất cả các cạnh của nó.

5. Tại sao cần học về ký hiệu chu vi?
Ký hiệu chu vi có nhiều ứng dụng trong thực tế, giúp giải quyết các vấn đề liên quan đến đo lường, thiết kế, xây dựng,…

6. Tôi có thể tìm thêm tài liệu và bài tập về ký hiệu chu vi ở đâu?
Bạn có thể tìm thấy nhiều tài liệu và bài tập về ký hiệu chu vi trên tic.edu.vn.

7. Làm thế nào để ghi nhớ công thức tính ký hiệu chu vi hiệu quả?
Bạn có thể áp dụng các mẹo như hiểu bản chất công thức, liên hệ với hình ảnh, sử dụng câu vè, thực hành thường xuyên,…

8. Ký hiệu chu vi được ứng dụng trong những lĩnh vực nào?
Ký hiệu chu vi được ứng dụng trong nhiều lĩnh vực như xây dựng, may mặc, nông nghiệp, thiết kế, thể thao,…

9. Có những sai lầm nào thường gặp khi tính ký hiệu chu vi?
Những sai lầm thường gặp bao gồm nhầm lẫn giữa chu vi và diện tích, không nhớ công thức, tính toán sai, không đổi đơn vị,…

10. Làm thế nào để cải thiện kỹ năng giải bài tập về ký hiệu chu vi?
Bạn cần nắm vững công thức, thực hành nhiều bài tập, và kiểm tra lại kết quả cẩn thận.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi bài toán về ký hiệu chu vi và đạt thành tích cao trong học tập. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để được hỗ trợ.