Kiến Thức Toán Lớp 4 Cần Ghi Nhớ Để Học Tốt

Kiến Thức Toán Lớp 4 Cần Ghi Nhớ là nền tảng vững chắc cho việc học toán ở các lớp trên, đặc biệt quan trọng khi các em bước vào lớp 5. Tic.edu.vn sẽ tổng hợp đầy đủ và chi tiết các kiến thức trọng tâm, giúp các em nắm vững kiến thức và tự tin hơn trong học tập. Hãy cùng tic.edu.vn khám phá những bí quyết học toán hiệu quả và chinh phục môn học này nhé.

1. Số Tự Nhiên Và Các Phép Tính

1.1. Số Và Chữ Số

Câu hỏi: Số và chữ số khác nhau như thế nào và có bao nhiêu số có một, hai, ba, bốn chữ số?

Trả lời: Chữ số là ký hiệu dùng để biểu diễn số, còn số là giá trị mà chúng ta đếm hoặc đo lường.

• Có 10 số có 1 chữ số (từ 0 đến 9).
• Có 90 số có 2 chữ số (từ 10 đến 99).
• Có 900 số có 3 chữ số (từ 100 đến 999).
• Có 9000 số có 4 chữ số (từ 1000 đến 9999).

Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc hiểu rõ sự khác biệt giữa số và chữ số giúp học sinh nắm vững cấu trúc số và thực hiện các phép tính chính xác hơn. Điều này rất quan trọng vì nó tạo nền tảng cho việc học các khái niệm toán học phức tạp hơn ở các lớp trên.

Số tự nhiên nhỏ nhất là 0 và không có số tự nhiên lớn nhất. Hai số tự nhiên liên tiếp hơn kém nhau một đơn vị. Các số có chữ số tận cùng là 0, 2, 4, 6, 8 gọi là số chẵn, hai số chẵn liên tiếp hơn kém nhau 2 đơn vị. Các số có chữ số tận cùng là 1, 3, 5, 7, 9 gọi là số lẻ, hai số lẻ liên tiếp hơn kém nhau 2 đơn vị.

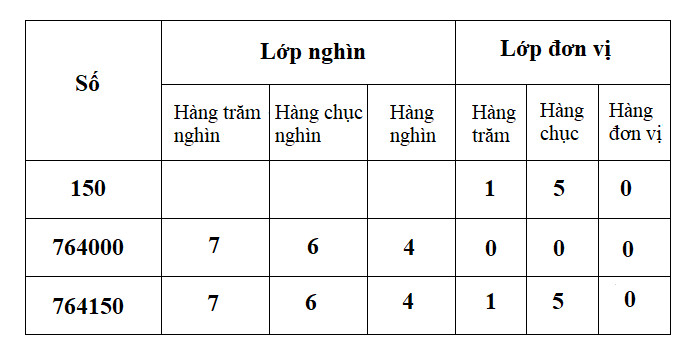
1.2. Hàng Và Lớp

Câu hỏi: Hàng và lớp trong số tự nhiên là gì và cách đọc số tự nhiên như thế nào?

Trả lời: Hàng là vị trí của một chữ số trong một số, còn lớp là tập hợp các hàng. Để đọc số tự nhiên, ta đọc từ trái sang phải, từ hàng cao đến hàng thấp.

Hàng đơn vị, hàng chục, hàng trăm hợp thành lớp đơn vị. Hàng nghìn, hàng chục nghìn, hàng trăm nghìn hợp thành lớp nghìn.

Theo báo cáo của Bộ Giáo dục và Đào tạo năm 2022, việc nắm vững cấu trúc hàng và lớp giúp học sinh đọc và viết số tự nhiên một cách chính xác, đồng thời hiểu rõ giá trị của mỗi chữ số trong số đó.

Ví dụ: Số 123.456.789 có:

• Lớp đơn vị: 789 (hàng trăm, hàng chục, hàng đơn vị)
• Lớp nghìn: 456 (hàng trăm nghìn, hàng chục nghìn, hàng nghìn)
• Lớp triệu: 123 (hàng trăm triệu, hàng chục triệu, hàng triệu)

1.3. Các Phép Tính Với Số Tự Nhiên

Câu hỏi: Các phép tính cộng, trừ, nhân, chia có những tính chất gì quan trọng?

Trả lời: Các phép tính có các tính chất giao hoán, kết hợp, phân phối giúp tính toán nhanh và chính xác hơn.

Phép cộng:

• Tính chất giao hoán: a + b = b + a
• Tính chất kết hợp: (a + b) + c = a + (b + c)
• Tính chất với số 0: 0 + a = a + 0 = a
• (a – n) + (b + n) = a + b
• (a – n) + (b – n) = a + b – n x 2
• (a + n) + (b + n) = a + b + n x 2
• Nếu một hạng được gấp lên n lần đồng thời các số hạng còn lại được giữ nguyên thì tổng đó được tăng lên một số đúng bằng (n – 1) lần số hạng được gấp lên
• Nếu số hạng bị giảm đi n lần, đồng thời các số hạng còn lại được giữ nguyên thì tổng đó bị giảm đi một số đúng bằng (1 -) số hạng bị giảm đi.
• Tổng của các số chẵn là một số chẵn
• Tổng của một số lẻ và một số chăn là một số lẻ
• Tổng của hai số tự nhiên liên tiếp là một số lẻ

Phép trừ:

• a – (b + c) = (a – c) – b = (a – b) – c
• Nếu số bị trừ và số trừ cùng tăng hoặc giảm n đơn vị thì hiệu của chúng không đổi
• Nếu số bị trừ được gấp lên n lần và giữ nguyên số trừ thì hiệu được tăng thêm một số đúng bằng (n – 1) lần số bị trừ
• Nếu số bị trừ giữ nguyên, số trừ được gấp lên n lần thì hiệu bị giảm đi (n – 1) lần số trừ
• Nếu số bị trừ được tăng thêm n đơn vị, số trừ giữ nguyên thì hiệu giảm đi n đơn vị

Phép nhân:

• Tính chất giao hoán: a x b = b x a
• Tính chất kết hợp: a x (b x c) = (a x b) x c
• Tính chất với số 0: a x 0 = 0 x a = 0
• Tính chất với số 1: a x 1 = 1 x a = a
• Tính chất phân phối: a x (b + c) = a x b + a x c
• a x (b – c) = a x b – a x c
• Trong một tích nếu thừa số được gấp lên n lần đồng thời có một thừa số khác bị giảm đi n lần thì tích không đổi.
• Trong một tích nếu thừa số được gấp lên n lần đồng thời, các thừa số còn lại giữ nguyên thì tích được gấp lên n lần và ngược lại trong một tích có một thừa số bị giảm đi n lần, các thừa số còn lại giữ nguyên thì tích cũng bị giảm đi n lần (n > 0)
• Trong một tích, nếu có ít nhất một thừa số chẵn thì tích đó chẵn
• Trong một tích, nếu một thừa số được tăng thêm a đơn vị các thừa số còn lại giữ nguyên thì tích được thêm a lần tích các thừa số còn lại.
• Trong một tích các thừa số đều lẻ và có ít nhất 1 thừa số có tận cùng là 5 thì tích có tận cùng là 5.

Phép chia:

• a : (b x c) = a : b : c = a : c : b (a,b > 0)
• 0 : a = 0
• a : c – b : c = (a – b) : c (c > 0)
• a : c + b : c = (a + b) : c (c > 0)
• Trong phép chia, nếu số bị chia tăng hoặc giảm đi n lần (n > 0) đồng thời số chia giữ nguyên thì thương cũng tăng lên (giảm đi) n lần.
• Trong một phép chia, nếu tăng số chia lên n lần (n > 0) đồng thời số bị chia giữ nguyên thì thương giảm đi n lần và ngược lại.
• Trong một phép chia, số chia và số bị chia cùng tăng hoặc giảm n lần thì thương không đổi.
• Trong một phép chia có dư, nếu số bị chia và số chia cùng được gấp (giảm) n lần (n > 0) thì số dư cũng được gấp (giảm) n lần.

1.4. Dãy Số

Câu hỏi: Làm thế nào để tìm ra quy luật của một dãy số và tính các số tiếp theo trong dãy?

Trả lời: Cần xác định khoảng cách giữa các số liên tiếp để tìm ra quy luật của dãy số.

Ví dụ: Dãy số 2, 4, 6, 8, … là dãy số chẵn, mỗi số hơn số liền trước 2 đơn vị. Số tiếp theo trong dãy là 10.

1.5. Dấu Hiệu Chia Hết

Câu hỏi: Các dấu hiệu chia hết cho 2, 3, 5, 9 là gì và chúng giúp ích gì trong việc giải toán?

Trả lời: Dấu hiệu chia hết giúp ta nhanh chóng xác định một số có chia hết cho các số 2, 3, 5, 9 hay không.

• Dấu hiệu chia hết cho 2: Các số có tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2.
• Dấu hiệu chia hết cho 5: Các số có tận cùng là 0, 5 thì chia hết cho 5.
• Dấu hiệu chia hết cho 3: Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.
• Dấu hiệu chia hết cho 9: Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.

Ví dụ: Số 123 chia hết cho 3 vì 1 + 2 + 3 = 6 chia hết cho 3.

2. Phân Số Và Các Phép Tính

2.1. Khái Niệm Phân Số

Câu hỏi: Phân số là gì và nó biểu thị điều gì?

Trả lời: Phân số là một số biểu thị một phần của một tổng thể, được viết dưới dạng a/b, trong đó a là tử số và b là mẫu số (b khác 0).

Ví dụ: Phân số 1/2 biểu thị một nửa của một cái bánh.

2.2. Tính Chất Cơ Bản Của Phân Số

Câu hỏi: Những tính chất cơ bản nào giúp ta biến đổi và so sánh phân số?

Trả lời: Tính chất cơ bản của phân số cho phép ta nhân hoặc chia cả tử và mẫu của một phân số cho cùng một số khác 0 mà không làm thay đổi giá trị của phân số đó.

• Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
• Nếu chia cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Ví dụ: 1/2 = (1×2)/(2×2) = 2/4

2.3. So Sánh Phân Số

Câu hỏi: Làm thế nào để so sánh các phân số có cùng mẫu số, cùng tử số và khác mẫu số?

Trả lời: Có các quy tắc so sánh phân số khác nhau tùy thuộc vào mẫu số và tử số của chúng.

• So sánh các phân số cùng mẫu số: Phân số nào có tử số lớn hơn thì lớn hơn.
• So sánh các phân số cùng tử số: Phân số nào có mẫu số bé hơn thì lớn hơn.
• So sánh các phân số khác mẫu số: Quy đồng mẫu số rồi so sánh tử số.

Ví dụ: So sánh 2/5 và 3/5: Vì 3 > 2 nên 3/5 > 2/5.

2.4. Các Phép Tính Với Phân Số

Câu hỏi: Làm thế nào để thực hiện các phép cộng, trừ, nhân, chia phân số?

Trả lời: Mỗi phép tính phân số có quy tắc riêng, cần nắm vững để thực hiện chính xác.

• Phép cộng phân số: Cùng mẫu số thì cộng tử số, khác mẫu số thì quy đồng rồi cộng.
• Phép trừ phân số: Cùng mẫu số thì trừ tử số, khác mẫu số thì quy đồng rồi trừ.
• Phép nhân phân số: Tử số nhân tử số, mẫu số nhân mẫu số.
• Phép chia phân số: Nhân với phân số đảo ngược.

Ví dụ: 1/2 + 1/3 = 3/6 + 2/6 = 5/6.

3. Các Đại Lượng Đo Lường

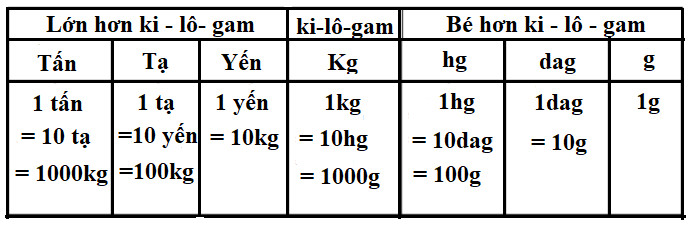
3.1. Bảng Đơn Vị Đo Khối Lượng

Câu hỏi: Các đơn vị đo khối lượng thông dụng là gì và mối quan hệ giữa chúng?

Trả lời: Các đơn vị đo khối lượng thông dụng bao gồm gam (g), kilogam (kg), yến, tạ, tấn, với mối quan hệ nhất định giữa chúng.

• 1 yến = 10 kg
• 1 tạ = 10 yến = 100 kg
• 1 tấn = 10 tạ = 1000 kg

Theo Tổng cục Thống kê Việt Nam, việc nắm vững bảng đơn vị đo khối lượng giúp học sinh ứng dụng kiến thức vào thực tế, ví dụ như trong các bài toán mua bán, cân đo.

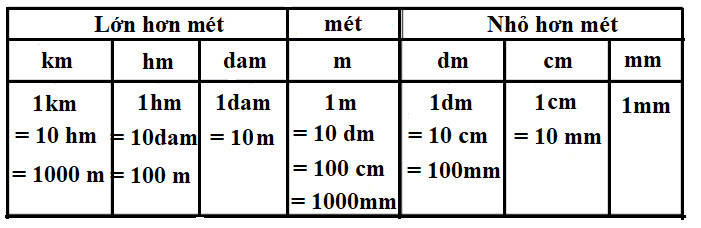
3.2. Bảng Đơn Vị Đo Độ Dài

Câu hỏi: Các đơn vị đo độ dài phổ biến là gì và làm thế nào để chuyển đổi giữa chúng?

Trả lời: Các đơn vị đo độ dài phổ biến bao gồm mét (m), kilômét (km), decimet (dm), centimet (cm), milimet (mm), với quy tắc chuyển đổi cụ thể.

• 1 km = 1000 m
• 1 m = 10 dm = 100 cm = 1000 mm
• 1 dm = 10 cm
• 1 cm = 10 mm

Một số đơn vị đo diện tích: m2, km2, dm2, cm2

• 1km2 = 1 000 000m2
• 1m2 = 100dm2
• 1m2 = 10 000cm2
• 1dm2 = 100cm2

3.3. Đơn Vị Thời Gian: Giây – Thế Kỷ

Câu hỏi: Các đơn vị đo thời gian thường dùng là gì và mối liên hệ giữa chúng?

Trả lời: Các đơn vị đo thời gian thường dùng là giây, phút, giờ, ngày, tháng, năm, thế kỷ, với các quy đổi cụ thể.

• 1 phút = 60 giây
• 1 giờ = 60 phút = 3600 giây
• 1 ngày = 24 giờ
• 1 năm = 365 ngày (năm nhuận có 366 ngày)
• 1 thế kỷ = 100 năm

Chú ý:

• Tháng một, tháng ba, tháng năm, tháng bảy, tháng 8, tháng mười, tháng mười hai có: 31 ngày.
• Tháng tư, tháng sáu, tháng chín, tháng mười một có: 30 ngày.
• Tháng hai có 28 ngày (vào năm nhuận có 29 ngày).

4. Số Trung Bình Cộng

4.1. Bài Toán Tìm Số Trung Bình Cộng

Câu hỏi: Làm thế nào để tính số trung bình cộng của nhiều số?

Trả lời: Tính tổng của các số rồi chia cho số các số hạng.

• Công thức: Trung bình cộng = (Tổng các số) / (Số các số hạng)

Ví dụ: Tìm trung bình cộng của 18, 19, 23: (18 + 19 + 23) : 3 = 20.

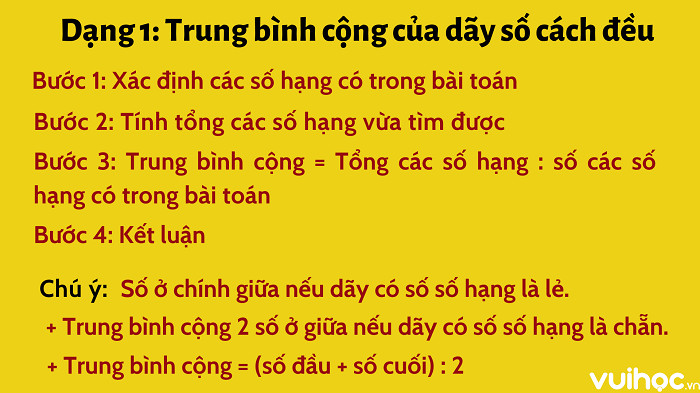
• Số trung bình cộng của dãy cách đều : (số đầu + số cuối) : 2

4.2. Bài Toán Tìm Số Hạng Khi Biết Trung Bình Cộng

Câu hỏi: Nếu biết trung bình cộng và một số số hạng, làm thế nào để tìm các số hạng còn lại?

Trả lời: Sử dụng sơ đồ hoặc phương pháp đại số để giải bài toán.

Ví dụ: Trung bình cộng của hai số là 25, một số là 30, tìm số còn lại: Số còn lại = 25 x 2 – 30 = 20.

5. Tìm Hai Số Khi Biết Tổng Và Hiệu

Câu hỏi: Làm thế nào để tìm hai số khi biết tổng và hiệu của chúng?

Trả lời: Áp dụng công thức: Số lớn = (Tổng + Hiệu) / 2, Số bé = (Tổng – Hiệu) / 2.

Ví dụ: Tổng hai số là 50, hiệu hai số là 10, tìm hai số: Số lớn = (50 + 10) / 2 = 30, Số bé = (50 – 10) / 2 = 20.

6. Tìm Hai Số Khi Biết Tổng (Hoặc Hiệu) Và Tỉ Số

6.1. Tìm Hai Số Khi Biết Tổng Và Tỉ Số

Câu hỏi: Làm thế nào để tìm hai số khi biết tổng và tỉ số của chúng?

Trả lời: Vẽ sơ đồ tỉ lệ, tìm tổng số phần bằng nhau, tìm giá trị một phần, rồi tìm từng số.

Ví dụ: Tổng hai số là 40, tỉ số của hai số là 2/3, tìm hai số: Tổng số phần bằng nhau là 2 + 3 = 5, Giá trị một phần là 40 / 5 = 8, Số bé = 8 x 2 = 16, Số lớn = 8 x 3 = 24.

6.2. Tìm Hai Số Khi Biết Hiệu Và Tỉ Số

Câu hỏi: Làm thế nào để tìm hai số khi biết hiệu và tỉ số của chúng?

Trả lời: Vẽ sơ đồ tỉ lệ, tìm hiệu số phần bằng nhau, tìm giá trị một phần, rồi tìm từng số.

Ví dụ: Hiệu hai số là 10, tỉ số của hai số là 3/5, tìm hai số: Hiệu số phần bằng nhau là 5 – 3 = 2, Giá trị một phần là 10 / 2 = 5, Số bé = 5 x 3 = 15, Số lớn = 5 x 5 = 25.

7. Đặt Tính Và Thực Hiện Phép Tính

7.1. Phép Nhân

Câu hỏi: Quy tắc đặt tính và thực hiện phép nhân là gì?

Trả lời: Đặt các chữ số thẳng hàng, nhân lần lượt từ phải sang trái, nhớ đặt tích riêng thẳng hàng.

• Khi thực hiện phép tính ta thực hiện từ phải qua trái
• Ta lần lượt có các tích riêng thứ 1, 2, 3… khi đặt tính nhớ phải đặt thẳng hàng các chữ số

7.2. Phép Chia

Câu hỏi: Quy tắc đặt tính và thực hiện phép chia là gì?

Trả lời: Chia lần lượt từ trái sang phải, thực hiện chia, nhân, trừ.

• Thực hiện phép tính theo thứ tự từ trái qua phải.
• Có đủ 3 phép tính trong phép chia gồm: Chia sau đó nhân rồi cuối cùng trừ.
• Trong phép chia có dư thì số dư bao giờ cũng nhỏ hơn số chia.

7.3. Phép Cộng

Câu hỏi: Quy tắc đặt tính và thực hiện phép cộng là gì?

Trả lời: Đặt các chữ số thẳng hàng, cộng lần lượt từ phải sang trái, nhớ số (nếu có).

Quy tắc: Muốn cộng hai số tự nhiên ta có thể làm như sau:

• Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
• Cộng các chữ số ở từng hàng theo thứ tự từ phải sang trái, tức là từ hàng đơn vị đến hàng chục, hàng trăm, hàng nghìn, … .

7.4. Phép Trừ

Câu hỏi: Quy tắc đặt tính và thực hiện phép trừ là gì?

Trả lời: Đặt các chữ số thẳng hàng, trừ lần lượt từ phải sang trái, mượn số (nếu cần).

Quy tắc: Muốn trừ hai số tự nhiên ta có thể làm như sau:

• Viết số hạng này dưới số hạng kia sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.
• Trừ các chữ số ở từng hàng theo thứ tự từ phải sang trái, tức là từ hàng đơn vị đến hàng chục, hàng trăm, hàng nghìn, …

8. Hình Học

8.1. Hình Bình Hành

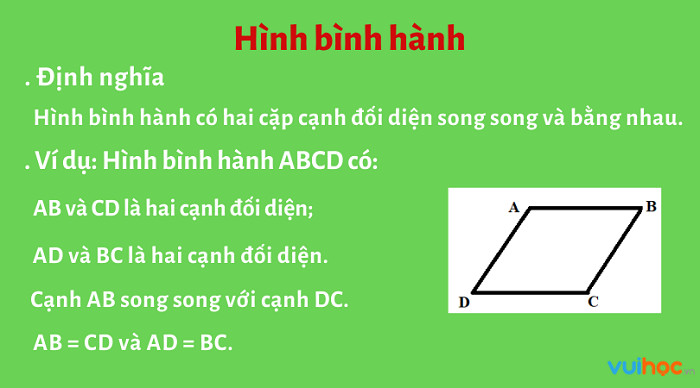
8.1.1. Nhận Biết Hình Bình Hành

Câu hỏi: Hình bình hành có những đặc điểm gì?

Trả lời: Hình bình hành là hình có hai cặp cạnh đối diện song song và bằng nhau.

8.1.2. Diện Tích Hình Bình Hành

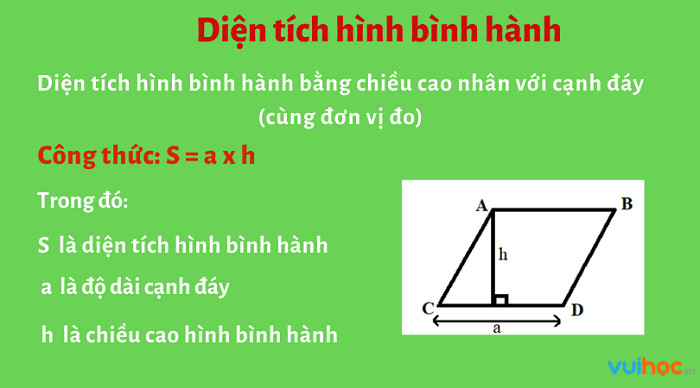
Câu hỏi: Làm thế nào để tính diện tích hình bình hành?

Trả lời: Diện tích hình bình hành bằng độ dài đáy nhân với chiều cao tương ứng.

• Công thức: S = a x h (trong đó a là độ dài đáy, h là chiều cao)

8.2. Hình Thoi

8.2.1. Nhận Biết Hình Thoi

Câu hỏi: Hình thoi có những đặc điểm gì?

Trả lời: Hình thoi là hình có bốn cạnh bằng nhau.

8.2.2. Diện Tích Hình Thoi

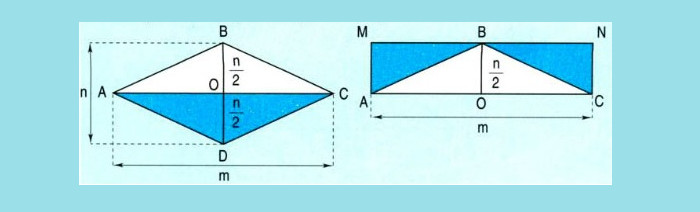
Câu hỏi: Làm thế nào để tính diện tích hình thoi?

Trả lời: Diện tích hình thoi bằng nửa tích của hai đường chéo.

• Công thức: S = (m x n) / 2 (trong đó m, n là độ dài hai đường chéo)

Ngoài ra, cần ghi nhớ thêm các kiến thức sau về hình học:

• Nếu tăng chiều dài của hình chữ nhật lên a đơn vị thì chu vi sẽ tăng lên a x 2
• Nếu tăng chiều rộng của hình chữ nhật lên a đơn vị thì chu vi sẽ tăng lên a x 2
• Nếu giảm chiều dài của hình chữ nhật lên a đơn vị thì chu vi sẽ giảm lên a x 2 đơn vị
• Nếu giảm chiều rộng của hình chữ nhật lên a đơn vị thì chu vi sẽ giảm lên a x 2 đơn vị
• Nếu gấp 1 chiều nào đó của hình chữ nhật lên bao nhiêu lần thì diện tích sẽ tăng lên bấy nhiêu lần.
• Nếu giảm 1 chiều nào đó của hình chữ nhật lên bao nhiêu lần thì diện tích sẽ giảm đi số lần
• Trong hình vuông, nếu tăng 1 cạnh lên a đơn vị thì chu vi sẽ tăng lên 4 x a đơn vị
• Trong hình vuông nếu cạnh tăng lên a lần thì diện tích tăng lên a x a lần

9. Các Dạng Toán Nâng Cao

Ngoài các kiến thức cơ bản, học sinh lớp 4 cũng cần làm quen với các dạng toán nâng cao như:

• Toán chuyển động đều: Tính vận tốc, thời gian, quãng đường.
• Toán trồng cây: Tính số cây, khoảng cách giữa các cây.
• Toán có yếu tố hình học: Kết hợp kiến thức hình học và số học để giải.

Để giải các bài toán nâng cao, học sinh cần nắm vững kiến thức cơ bản, có tư duy logic và khả năng phân tích đề bài.

10. FAQ – Các Câu Hỏi Thường Gặp Về Toán Lớp 4

Câu hỏi 1: Làm thế nào để học tốt môn Toán lớp 4?

Trả lời: Nắm vững kiến thức cơ bản, làm nhiều bài tập, tìm hiểu các dạng toán nâng cao, và hỏi thầy cô khi gặp khó khăn.

Câu hỏi 2: Nên sử dụng sách tham khảo nào cho môn Toán lớp 4?

Trả lời: Các sách tham khảo nên dùng là “Vở bài tập Toán 4”, “Nâng cao và phát triển Toán 4”, và các sách luyện thi học sinh giỏi Toán.

Câu hỏi 3: Làm thế nào để giúp con tự học Toán lớp 4 hiệu quả?

Trả lời: Tạo không gian học tập yên tĩnh, khuyến khích con tự giải bài tập, và cùng con kiểm tra kết quả.

Câu hỏi 4: Có nên cho con học thêm Toán lớp 4 không?

Trả lời: Nếu con gặp khó khăn trong học tập hoặc muốn nâng cao kiến thức, học thêm là một lựa chọn tốt.

Câu hỏi 5: Làm thế nào để giúp con yêu thích môn Toán?

Trả lời: Tạo ra các trò chơi toán học, liên hệ toán học với thực tế, và khen ngợi khi con đạt thành tích tốt.

Câu hỏi 6: Làm thế nào để giải bài toán có lời văn hiệu quả?

Trả lời: Đọc kỹ đề bài, xác định các yếu tố đã cho và cần tìm, lập kế hoạch giải, và trình bày lời giải rõ ràng.

Câu hỏi 7: Các lỗi thường gặp khi giải toán lớp 4 là gì?

Trả lời: Các lỗi thường gặp bao gồm tính toán sai, nhầm lẫn công thức, và không hiểu rõ đề bài.

Câu hỏi 8: Làm thế nào để kiểm tra lại bài giải Toán?

Trả lời: Kiểm tra lại các bước tính toán, đối chiếu kết quả với đề bài, và thử một phương pháp giải khác (nếu có).

Câu hỏi 9: Tại sao cần học thuộc bảng cửu chương?

Trả lời: Học thuộc bảng cửu chương giúp tính toán nhanh và chính xác hơn, đặc biệt trong các phép nhân và chia.

Câu hỏi 10: Làm thế nào để rèn luyện tư duy logic trong môn Toán?

Trả lời: Giải các bài toán đố, tham gia các câu lạc bộ toán học, và đọc các sách về tư duy logic.

tic.edu.vn hy vọng rằng với những kiến thức toán lớp 4 cần ghi nhớ được tổng hợp trên đây, các em