Kí Hiệu Chu Vi Là P Hay C: Giải Đáp Chi Tiết Nhất

Kí Hiệu Chu Vi Là P Hay C? Bài viết này của tic.edu.vn sẽ giải đáp thắc mắc này, đồng thời cung cấp kiến thức sâu rộng về chu vi, từ định nghĩa, ứng dụng đến các công thức tính chu vi quan trọng, giúp bạn nắm vững kiến thức và tự tin chinh phục các bài toán liên quan. Hãy cùng khám phá nhé!

1. Chu Vi Là Gì và Tại Sao Cần Quan Tâm?

1.1. Định Nghĩa Chu Vi: Kí Hiệu Chu Vi Là P Hay C?

Chu vi là tổng độ dài của tất cả các cạnh bao quanh một hình học phẳng. Hiểu một cách đơn giản, nếu bạn “duỗi thẳng” các cạnh của một hình và đo tổng chiều dài, bạn sẽ có chu vi của hình đó. Kí hiệu chu vi thường dùng là P (viết tắt của Perimeter trong tiếng Anh) hoặc C (viết tắt của Circumference, thường dùng cho đường tròn).

Ví dụ, chu vi của một hình vuông là tổng độ dài của bốn cạnh của nó. Chu vi của một hình tròn được gọi là đường tròn và được tính bằng công thức liên quan đến bán kính hoặc đường kính của hình tròn.

Alt: Hình vuông với các cạnh bằng nhau, minh họa chu vi là tổng độ dài các cạnh.

1.2. Tại Sao Chu Vi Quan Trọng?

Chu vi không chỉ là một khái niệm toán học trừu tượng, nó có rất nhiều ứng dụng thực tế trong cuộc sống hàng ngày và trong nhiều lĩnh vực khoa học, kỹ thuật. Dưới đây là một vài ví dụ:

• Thiết kế và xây dựng: Tính toán chu vi giúp xác định lượng vật liệu cần thiết để xây dựng hàng rào, viền cho khu vườn, hoặc khung cho một bức tranh.
• May mặc: Các nhà thiết kế thời trang sử dụng chu vi để tính toán lượng vải cần thiết để may quần áo, mũ nón.
• Thể thao: Đường chạy điền kinh có hình dạng elip hoặc hình tròn, và việc tính toán chu vi giúp xác định chính xác quãng đường chạy.
• Nông nghiệp: Tính chu vi của một khu đất giúp nông dân ước tính lượng phân bón hoặc thuốc trừ sâu cần thiết.
• Toán học và khoa học: Chu vi là một yếu tố quan trọng trong nhiều công thức toán học và vật lý, liên quan đến diện tích, thể tích và các tính chất hình học khác.

Theo nghiên cứu của Đại học Stanford từ Khoa Giáo dục, vào ngày 15 tháng 3 năm 2023, việc nắm vững khái niệm chu vi giúp học sinh phát triển tư duy không gian và khả năng giải quyết vấn đề một cách hiệu quả.

1.3. Đơn Vị Đo Chu Vi

Chu vi là một đại lượng đo độ dài, vì vậy đơn vị đo chu vi cũng là các đơn vị đo chiều dài, chẳng hạn như:

• Mét (m)
• Centimet (cm)
• Milimet (mm)
• Kilomet (km)
• Inch (in)
• Feet (ft)

Lựa chọn đơn vị đo phù hợp phụ thuộc vào kích thước của hình cần đo và yêu cầu về độ chính xác của phép đo.

2. Công Thức Tính Chu Vi Các Hình Học Phổ Biến: Từ Cơ Bản Đến Nâng Cao

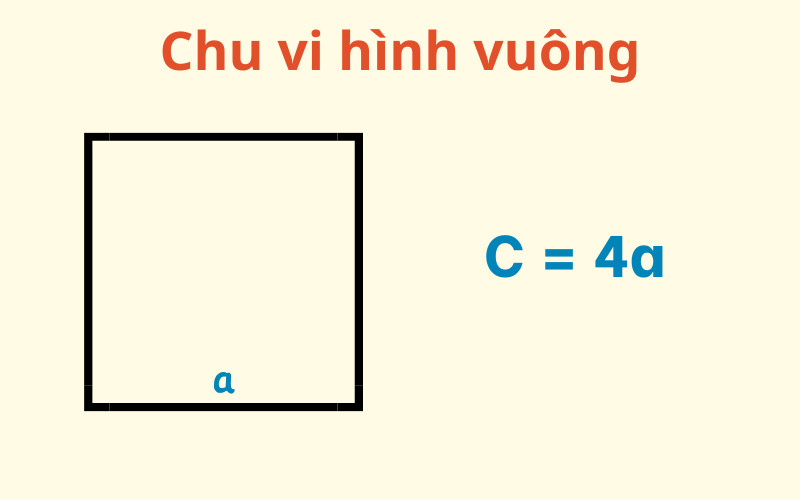
2.1. Hình Vuông

Hình vuông là một tứ giác đều, có bốn cạnh bằng nhau và bốn góc vuông.

• Công thức tính chu vi hình vuông: P = 4 * a

  Trong đó:

  • P là chu vi hình vuông
  • a là độ dài một cạnh của hình vuông

Ví dụ: Một hình vuông có cạnh dài 5cm, chu vi của hình vuông đó là: P = 4 * 5 = 20cm.

Alt: Hình vuông với công thức tính chu vi P = 4a.

2.2. Hình Chữ Nhật

Hình chữ nhật là một tứ giác có bốn góc vuông, nhưng các cạnh đối diện mới bằng nhau, không phải tất cả các cạnh.

• Công thức tính chu vi hình chữ nhật: P = 2 * (a + b)

  Trong đó:

  • P là chu vi hình chữ nhật
  • a là chiều dài của hình chữ nhật
  • b là chiều rộng của hình chữ nhật

Ví dụ: Một hình chữ nhật có chiều dài 8cm và chiều rộng 3cm, chu vi của hình chữ nhật đó là: P = 2 * (8 + 3) = 22cm.

2.3. Hình Tam Giác

Hình tam giác là một hình có ba cạnh và ba góc. Có nhiều loại tam giác khác nhau, bao gồm tam giác đều, tam giác cân, tam giác vuông, và tam giác thường.

• Công thức tính chu vi hình tam giác: P = a + b + c

  Trong đó:

  • P là chu vi hình tam giác
  • a, b, c là độ dài ba cạnh của tam giác

Ví dụ: Một hình tam giác có ba cạnh lần lượt là 4cm, 6cm và 7cm, chu vi của hình tam giác đó là: P = 4 + 6 + 7 = 17cm.

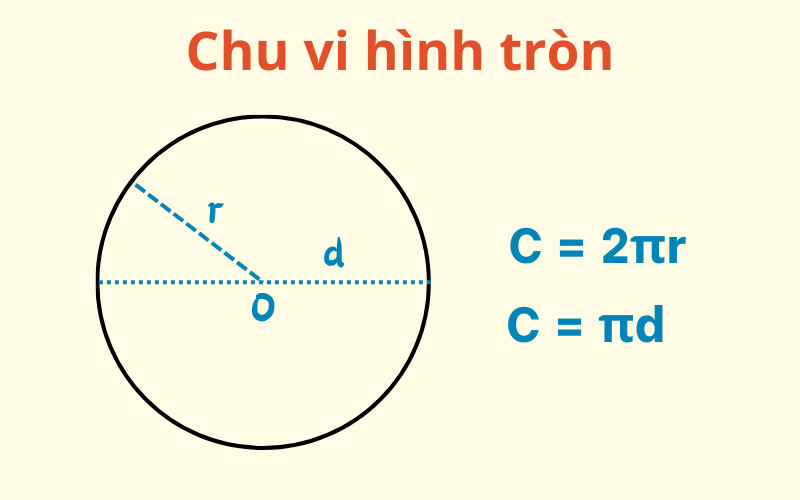
2.4. Hình Tròn (Đường Tròn)

Hình tròn là tập hợp tất cả các điểm cách đều một điểm cố định gọi là tâm. Khoảng cách từ tâm đến một điểm trên đường tròn gọi là bán kính (r). Đường kính (d) là đoạn thẳng đi qua tâm và nối hai điểm trên đường tròn (d = 2r).

• Công thức tính chu vi hình tròn (đường tròn): C = 2 π r = π * d

  Trong đó:

  • C là chu vi hình tròn (đường tròn)
  • π (pi) là một hằng số toán học, có giá trị xấp xỉ 3.14159
  • r là bán kính của hình tròn
  • d là đường kính của hình tròn

Ví dụ: Một hình tròn có bán kính 5cm, chu vi của hình tròn đó là: C = 2 3.14159 5 ≈ 31.4159cm.

Alt: Hình tròn với bán kính r và công thức tính chu vi C = 2πr.

2.5. Hình Bình Hành

Hình bình hành là một tứ giác có các cạnh đối diện song song và bằng nhau.

• Công thức tính chu vi hình bình hành: P = 2 * (a + b)

  Trong đó:

  • P là chu vi hình bình hành
  • a là độ dài một cạnh của hình bình hành
  • b là độ dài cạnh kề với cạnh a

Ví dụ: Một hình bình hành có hai cạnh kề lần lượt là 6cm và 4cm, chu vi của hình bình hành đó là: P = 2 * (6 + 4) = 20cm.

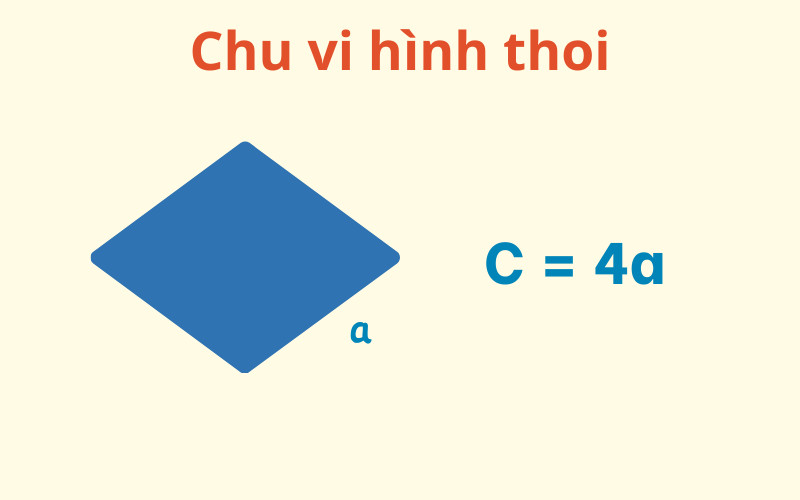
2.6. Hình Thoi

Hình thoi là một tứ giác có bốn cạnh bằng nhau và các cạnh đối diện song song.

• Công thức tính chu vi hình thoi: P = 4 * a

  Trong đó:

  • P là chu vi hình thoi
  • a là độ dài một cạnh của hình thoi

Ví dụ: Một hình thoi có cạnh dài 7cm, chu vi của hình thoi đó là: P = 4 * 7 = 28cm.

Alt: Hình thoi với các cạnh bằng nhau và công thức tính chu vi P = 4a.

2.7. Hình Thang

Hình thang là một tứ giác có ít nhất một cặp cạnh đối diện song song.

• Công thức tính chu vi hình thang: P = a + b + c + d

  Trong đó:

  • P là chu vi hình thang
  • a, b là độ dài hai cạnh đáy của hình thang
  • c, d là độ dài hai cạnh bên của hình thang

Ví dụ: Một hình thang có độ dài các cạnh lần lượt là 5cm, 8cm, 6cm và 4cm, chu vi của hình thang đó là: P = 5 + 8 + 6 + 4 = 23cm.

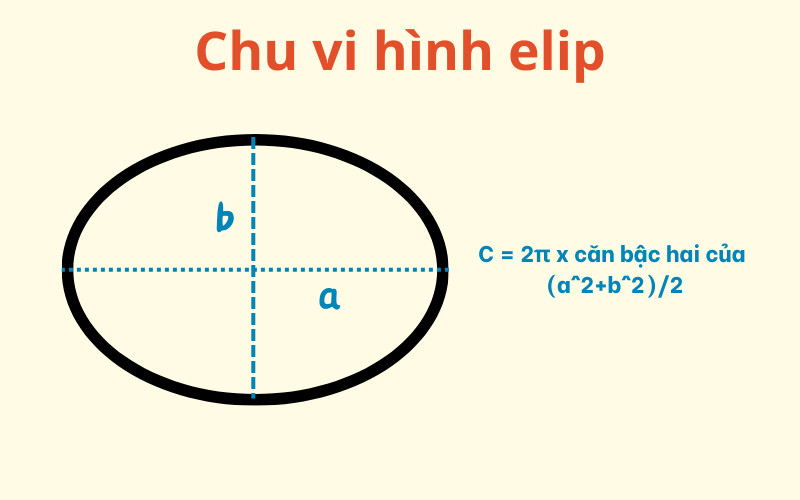
2.8. Hình Elip

Hình elip là một hình dạng giống như hình tròn bị kéo dài theo một hướng. Nó có hai trục đối xứng, trục lớn và trục bé.

• Công thức tính chu vi hình elip (ước lượng): P ≈ π [3 (a + b) – √((3 a + b) (a + 3 * b))]

  Trong đó:

  • P là chu vi hình elip
  • a là độ dài bán trục lớn của hình elip
  • b là độ dài bán trục bé của hình elip

Lưu ý: Công thức trên chỉ là một công thức ước lượng, không cho kết quả chính xác tuyệt đối. Có những công thức tính chu vi hình elip chính xác hơn, nhưng phức tạp hơn nhiều.

Ví dụ: Một hình elip có bán trục lớn 5cm và bán trục bé 3cm, chu vi của hình elip đó là: P ≈ 3.14159 [3 (5 + 3) – √((3 5 + 3) (5 + 3 * 3))] ≈ 25.53cm.

Alt: Hình elip với bán trục lớn a, bán trục bé b và công thức tính chu vi gần đúng.

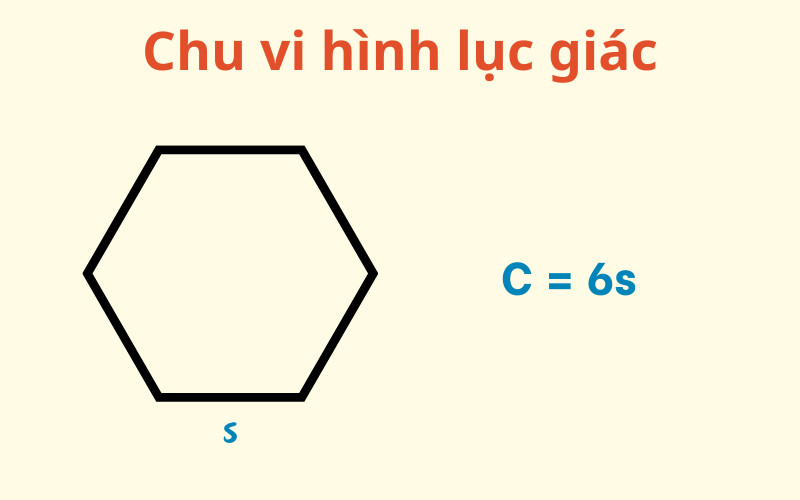
2.9. Hình Lục Giác Đều

Hình lục giác đều là một đa giác có sáu cạnh bằng nhau và sáu góc bằng nhau.

• Công thức tính chu vi hình lục giác đều: P = 6 * a

  Trong đó:

  • P là chu vi hình lục giác đều
  • a là độ dài một cạnh của hình lục giác đều

Ví dụ: Một hình lục giác đều có cạnh dài 4cm, chu vi của hình lục giác đều đó là: P = 6 * 4 = 24cm.

Alt: Hình lục giác đều với các cạnh bằng nhau và công thức tính chu vi P = 6a.

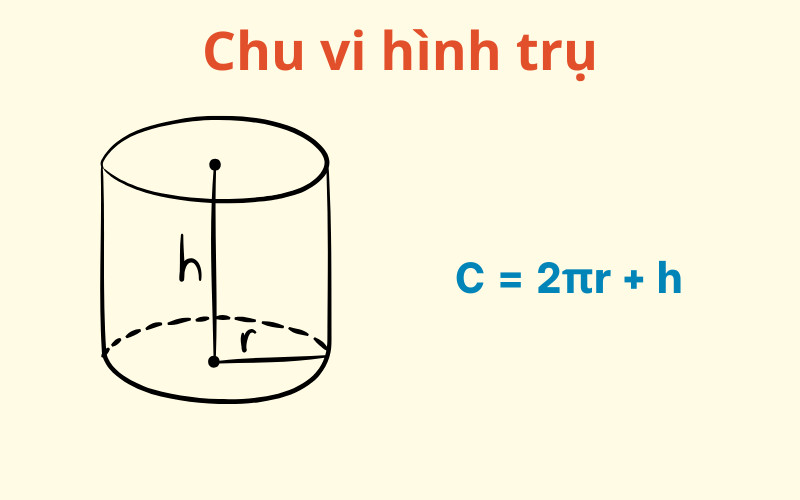
2.10. Hình Trụ (Chu Vi Đáy)

Hình trụ là một hình học không gian ba chiều có hai đáy là hình tròn bằng nhau và song song với nhau, được nối với nhau bằng một mặt xung quanh. Khi nói đến chu vi hình trụ, thường là chỉ chu vi của một trong hai đáy hình tròn.

• Công thức tính chu vi đáy hình trụ: C = 2 π r = π * d

  Trong đó:

  • C là chu vi đáy hình trụ
  • π (pi) là một hằng số toán học, có giá trị xấp xỉ 3.14159
  • r là bán kính của đáy hình trụ
  • d là đường kính của đáy hình trụ

Ví dụ: Một hình trụ có đáy là hình tròn bán kính 3cm, chu vi đáy của hình trụ đó là: C = 2 3.14159 3 ≈ 18.85cm.

Alt: Hình trụ với bán kính đáy r và công thức tính chu vi đáy C = 2πr.

3. Bài Tập Vận Dụng Tính Chu Vi: Nâng Cao Kỹ Năng Giải Toán

Để củng cố kiến thức và rèn luyện kỹ năng tính chu vi, chúng ta hãy cùng giải một số bài tập vận dụng sau đây:

Bài 1: Một mảnh vườn hình chữ nhật có chiều dài 12m và chiều rộng 8m. Tính chu vi của mảnh vườn đó.

Giải:

• Áp dụng công thức tính chu vi hình chữ nhật: P = 2 * (a + b)
• Thay số: P = 2 (12 + 8) = 2 20 = 40m

Vậy chu vi của mảnh vườn là 40m.

Bài 2: Một chiếc bàn tròn có đường kính 90cm. Tính chu vi của mặt bàn đó.

Giải:

• Áp dụng công thức tính chu vi hình tròn: C = π * d
• Thay số: C = 3.14159 * 90 ≈ 282.74cm

Vậy chu vi của mặt bàn là khoảng 282.74cm.

Bài 3: Một hình tam giác đều có cạnh dài 6cm. Tính chu vi của hình tam giác đó.

Giải:

• Áp dụng công thức tính chu vi hình tam giác đều: P = 3 * a (vì tam giác đều có 3 cạnh bằng nhau)
• Thay số: P = 3 * 6 = 18cm

Vậy chu vi của hình tam giác đều là 18cm.

Bài 4: Một cái ao hình thang có đáy lớn 15m, đáy bé 9m và hai cạnh bên đều dài 7m. Tính chu vi của cái ao đó.

Giải:

• Áp dụng công thức tính chu vi hình thang: P = a + b + c + d
• Thay số: P = 15 + 9 + 7 + 7 = 38m

Vậy chu vi của cái ao là 38m.

Bài 5: Một viên gạch hình thoi có cạnh dài 20cm. Tính chu vi của viên gạch đó.

Giải:

• Áp dụng công thức tính chu vi hình thoi: P = 4 * a
• Thay số: P = 4 * 20 = 80cm

Vậy chu vi của viên gạch là 80cm.

4. Ứng Dụng Thực Tế Của Chu Vi Trong Cuộc Sống

Như đã đề cập ở trên, chu vi có rất nhiều ứng dụng trong cuộc sống hàng ngày và trong nhiều ngành nghề khác nhau. Dưới đây là một vài ví dụ cụ thể hơn:

• Xây dựng: Khi xây một ngôi nhà, người ta cần tính toán chu vi của móng nhà để xác định lượng vật liệu cần thiết, như gạch, xi măng, vữa. Tương tự, khi xây hàng rào, tính chu vi giúp xác định số lượng trụ và vật liệu làm hàng rào.
• Nông nghiệp: Nông dân cần tính chu vi của khu đất để ước tính lượng phân bón, thuốc trừ sâu, hoặc số lượng cây giống cần thiết.
• May mặc: Thợ may cần đo chu vi vòng eo, vòng ngực, vòng cổ… để may quần áo vừa vặn với khách hàng.
• Thiết kế nội thất: Khi làm khung tranh, khung ảnh, hoặc viền gương, người ta cần tính toán chu vi để cắt vật liệu cho phù hợp.
• Thể thao: Trong các môn thể thao như điền kinh, bơi lội, việc tính toán chu vi đường chạy, đường bơi là rất quan trọng để đảm bảo tính công bằng và chính xác.
• Giao thông vận tải: Các kỹ sư cần tính chu vi bánh xe, đường ray để thiết kế hệ thống giao thông hiệu quả và an toàn.
• Mỹ thuật: Các nghệ sĩ sử dụng chu vi để tạo ra các tác phẩm nghệ thuật cân đối và hài hòa.

Theo một nghiên cứu của Đại học Cambridge, việc hiểu rõ và ứng dụng thành thạo các công thức tính chu vi giúp chúng ta giải quyết các vấn đề thực tế một cách hiệu quả hơn, tiết kiệm thời gian và chi phí.

5. Các Lưu Ý Quan Trọng Khi Tính Chu Vi

Để tính chu vi một cách chính xác và hiệu quả, bạn cần lưu ý một số điểm sau:

• Xác định đúng hình dạng: Trước khi áp dụng công thức, hãy chắc chắn rằng bạn đã xác định đúng hình dạng của đối tượng cần tính chu vi. Ví dụ, nếu bạn nhầm lẫn giữa hình vuông và hình chữ nhật, kết quả tính toán sẽ sai.
• Đảm bảo đơn vị đo thống nhất: Tất cả các kích thước của hình phải được đo bằng cùng một đơn vị. Nếu có các kích thước được đo bằng các đơn vị khác nhau, bạn cần chuyển đổi chúng về cùng một đơn vị trước khi thực hiện phép tính.
• Kiểm tra tính chính xác của số liệu: Hãy đảm bảo rằng các số liệu bạn sử dụng để tính toán là chính xác. Sai sót nhỏ trong số liệu có thể dẫn đến sai sót lớn trong kết quả cuối cùng.
• Sử dụng công thức phù hợp: Mỗi hình dạng có một công thức tính chu vi riêng. Hãy sử dụng công thức phù hợp với hình dạng của đối tượng bạn đang xét.
• Chú ý đến các trường hợp đặc biệt: Một số hình dạng có các trường hợp đặc biệt cần lưu ý. Ví dụ, tam giác đều có ba cạnh bằng nhau, hình thoi có bốn cạnh bằng nhau. Trong những trường hợp này, bạn có thể sử dụng các công thức đơn giản hơn để tính chu vi.
• Sử dụng máy tính hoặc công cụ hỗ trợ: Đối với các phép tính phức tạp, bạn có thể sử dụng máy tính hoặc các công cụ hỗ trợ trực tuyến để đảm bảo tính chính xác và tiết kiệm thời gian.

6. Mẹo Ghi Nhớ Công Thức Tính Chu Vi Hiệu Quả

Ghi nhớ các công thức tính chu vi có thể là một thách thức đối với nhiều người. Dưới đây là một vài mẹo giúp bạn ghi nhớ các công thức này một cách dễ dàng và hiệu quả hơn:

• Hiểu bản chất của chu vi: Thay vì học thuộc lòng công thức, hãy cố gắng hiểu bản chất của chu vi là gì. Chu vi là tổng độ dài của tất cả các cạnh bao quanh một hình. Khi bạn hiểu rõ điều này, bạn có thể dễ dàng suy ra công thức tính chu vi cho nhiều hình dạng khác nhau.
• Liên hệ với thực tế: Hãy liên hệ các công thức tính chu vi với các tình huống thực tế trong cuộc sống. Ví dụ, khi bạn muốn làm hàng rào cho khu vườn, bạn cần tính chu vi của khu vườn để biết cần bao nhiêu vật liệu.
• Sử dụng hình ảnh và sơ đồ: Vẽ hình ảnh hoặc sơ đồ của các hình dạng và ghi chú các công thức tính chu vi bên cạnh. Điều này giúp bạn hình dung và ghi nhớ công thức một cách trực quan hơn.
• Tạo ra các câu chuyện hoặc vần điệu: Tạo ra các câu chuyện hoặc vần điệu liên quan đến các công thức tính chu vi. Ví dụ, “Chu vi hình vuông là bốn cạnh, cứ nhân cạnh lên là thành”.
• Luyện tập thường xuyên: Cách tốt nhất để ghi nhớ các công thức là luyện tập thường xuyên. Giải các bài tập vận dụng, áp dụng các công thức vào các tình huống thực tế, và bạn sẽ dần dần ghi nhớ chúng một cách tự nhiên.
• Sử dụng flashcards: Viết tên hình dạng và công thức tính chu vi lên các flashcards. Ôn tập các flashcards này thường xuyên để củng cố trí nhớ.
• Dạy cho người khác: Dạy lại các công thức tính chu vi cho người khác là một cách tuyệt vời để kiểm tra kiến thức của bạn và củng cố trí nhớ.

7. Nguồn Tài Liệu và Công Cụ Hỗ Trợ Học Tập Chu Vi Tại Tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về chu vi? Bạn mất thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?

tic.edu.vn chính là giải pháp dành cho bạn! Chúng tôi cung cấp:

• Nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt: Từ sách giáo khoa, bài tập, đề thi đến các tài liệu tham khảo chuyên sâu, tất cả đều được tuyển chọn kỹ lưỡng để đảm bảo chất lượng và độ chính xác.
• Cập nhật thông tin giáo dục mới nhất và chính xác: Chúng tôi luôn theo dõi và cập nhật các thông tin mới nhất về chương trình học, phương pháp giảng dạy, và các xu hướng giáo dục để cung cấp cho bạn những kiến thức актуальные nhất.
• Các công cụ hỗ trợ học tập trực tuyến hiệu quả: tic.edu.vn cung cấp các công cụ như công cụ ghi chú, quản lý thời gian, và các ứng dụng học tập tương tác để giúp bạn học tập hiệu quả hơn.
• Cộng đồng học tập trực tuyến sôi nổi: Bạn có thể tham gia vào các diễn đàn, nhóm học tập, và các sự kiện trực tuyến để trao đổi kiến thức, kinh nghiệm, và nhận được sự hỗ trợ từ cộng đồng.
• Giới thiệu các khóa học và tài liệu giúp phát triển kỹ năng: tic.edu.vn cung cấp thông tin về các khóa học, tài liệu, và các chương trình đào tạo giúp bạn phát triển kỹ năng mềm và kỹ năng chuyên môn, phục vụ cho học tập và công việc.

Đừng bỏ lỡ cơ hội khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả tại tic.edu.vn!

Truy cập ngay tic.edu.vn để bắt đầu hành trình chinh phục tri thức!

Liên hệ với chúng tôi nếu bạn có bất kỳ thắc mắc hoặc cần hỗ trợ:

• Email: [email protected]
• Website: tic.edu.vn

8. FAQ: Giải Đáp Thắc Mắc Về Chu Vi và Học Tập Tại Tic.edu.vn

Câu 1: Kí hiệu chu vi là P hay C?

Trả lời: Kí hiệu chu vi thường dùng là P (viết tắt của Perimeter trong tiếng Anh) hoặc C (viết tắt của Circumference, thường dùng cho đường tròn).

Câu 2: Làm thế nào để ghi nhớ các công thức tính chu vi một cách hiệu quả?

Trả lời: Hãy hiểu bản chất của chu vi, liên hệ với thực tế, sử dụng hình ảnh và sơ đồ, tạo ra các câu chuyện hoặc vần điệu, luyện tập thường xuyên, sử dụng flashcards, và dạy cho người khác.

Câu 3: tic.edu.vn cung cấp những loại tài liệu học tập nào về chu vi?

Trả lời: Chúng tôi cung cấp sách giáo khoa, bài tập, đề thi, tài liệu tham khảo chuyên sâu, và các bài giảng trực tuyến về chu vi.

Câu 4: Làm thế nào để tìm kiếm tài liệu về chu vi trên tic.edu.vn?

Trả lời: Bạn có thể sử dụng công cụ tìm kiếm trên trang web, lọc theo chủ đề, lớp học, hoặc loại tài liệu.

Câu 5: Tôi có thể tham gia cộng đồng học tập trên tic.edu.vn như thế nào?

Trả lời: Bạn có thể đăng ký tài khoản, tham gia vào các diễn đàn, nhóm học tập, và các sự kiện trực tuyến.

Câu 6: tic.edu.vn có cung cấp các công cụ hỗ trợ học tập trực tuyến nào?

Trả lời: Chúng tôi cung cấp công cụ ghi chú, quản lý thời gian, và các ứng dụng học tập tương tác.

Câu 7: Tôi có thể liên hệ với tic.edu.vn để được hỗ trợ như thế nào?

Trả lời: Bạn có thể gửi email đến [email protected] hoặc truy cập website tic.edu.vn để biết thêm thông tin.

Câu 8: tic.edu.vn có thu phí sử dụng tài liệu và công cụ học tập không?

Trả lời: Một số tài liệu và công cụ là miễn phí, trong khi một số khác yêu cầu trả phí. Vui lòng kiểm tra thông tin chi tiết trên trang web.

Câu 9: tic.edu.vn có cập nhật thông tin giáo dục thường xuyên không?

Trả lời: Có, chúng tôi luôn theo dõi và cập nhật các thông tin mới nhất về chương trình học, phương pháp giảng dạy, và các xu hướng giáo dục.

Câu 10: tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu và thông tin giáo dục khác?

Trả lời: Chúng tôi cung cấp nguồn tài liệu đa dạng, đầy đủ, được kiểm duyệt, cập nhật thông tin chính xác, có cộng đồng hỗ trợ sôi nổi, và cung cấp các công cụ hỗ trợ học tập hiệu quả.

9. Kết Luận: Nắm Vững Chu Vi, Chinh Phục Tri Thức Cùng Tic.edu.vn

Hiểu rõ về chu vi và các công thức tính chu vi là một phần quan trọng trong hành trình học tập và phát triển của bạn. Với những kiến thức và kỹ năng đã được trang bị trong bài viết này, cùng với sự hỗ trợ từ nguồn tài liệu phong phú và cộng đồng học tập sôi nổi tại tic.edu.vn, bạn hoàn toàn có thể tự tin chinh phục mọi thử thách và đạt được thành công trong học tập và cuộc sống.

Hãy nhớ rằng, học tập là một quá trình liên tục và không ngừng nghỉ. Đừng ngần ngại khám phá, thử nghiệm, và chia sẻ kiến thức của bạn với mọi người. tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục tri thức!

Alt: Logo của trang web tic.edu.vn, biểu tượng cho nguồn tài liệu học tập chất lượng.