**Khoảng Cách Hai Đường Thẳng Chéo Nhau: Định Nghĩa, Cách Tính & Bài Tập**

Khoảng cách hai đường thẳng chéo nhau là một khái niệm quan trọng trong hình học không gian, đặc biệt trong chương trình Toán học phổ thông. Bạn đang tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về chủ đề này? Bài viết này tại tic.edu.vn sẽ cung cấp cho bạn định nghĩa, các phương pháp tính toán, và bài tập vận dụng để bạn nắm vững kiến thức này một cách hiệu quả. Hãy cùng tic.edu.vn khám phá bí quyết chinh phục dạng toán này một cách dễ dàng và tự tin bạn nhé.

1. Hiểu Rõ Về Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau

Bạn có bao giờ tự hỏi khoảng cách giữa hai đường thẳng chéo nhau được định nghĩa như thế nào?

Trả lời: Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó.

Mở rộng: Trong không gian ba chiều, hai đường thẳng có thể có nhiều vị trí tương đối khác nhau: trùng nhau, cắt nhau, song song hoặc chéo nhau. Khi hai đường thẳng ở vị trí chéo nhau, tức là chúng không cắt nhau và không cùng nằm trên một mặt phẳng, việc xác định khoảng cách giữa chúng trở nên thú vị. Đoạn vuông góc chung chính là đoạn thẳng ngắn nhất nối hai đường thẳng này và vuông góc với cả hai. Hãy tưởng tượng bạn đang cố gắng đo khoảng cách giữa hai con đường trên hai cây cầu khác nhau không giao nhau; đoạn vuông góc chung chính là “thước đo” chính xác nhất.

1.1. Tính Duy Nhất Của Đoạn Vuông Góc Chung

Vậy, có bao nhiêu đoạn vuông góc chung giữa hai đường thẳng chéo nhau?

Trả lời: Đoạn vuông góc chung của hai đường thẳng chéo nhau là duy nhất.

Mở rộng: Tính duy nhất này rất quan trọng trong các bài toán hình học không gian. Điều này có nghĩa là bạn chỉ cần tìm ra một đoạn thẳng thỏa mãn điều kiện vuông góc với cả hai đường thẳng và nối hai điểm trên hai đường thẳng đó thì đó chính là đoạn vuông góc chung duy nhất và ngắn nhất. Nhờ tính chất này, việc giải các bài toán liên quan đến khoảng cách giữa hai đường thẳng chéo nhau trở nên dễ dàng và chính xác hơn.

2. Khám Phá Các Phương Pháp Tính Khoảng Cách Hiệu Quả

Làm thế nào để tính khoảng cách giữa hai đường thẳng chéo nhau một cách chính xác và nhanh chóng?

Trả lời: Có nhiều phương pháp khác nhau để tính khoảng cách giữa hai đường thẳng chéo nhau, bao gồm phương pháp dựng đoạn vuông góc chung, phương pháp sử dụng mặt phẳng song song và phương pháp sử dụng tích có hướng của hai vectơ chỉ phương.

Mở rộng: Để giải quyết các bài toán về khoảng cách giữa hai đường thẳng chéo nhau, bạn cần nắm vững các kỹ năng dựng hình, tính toán và áp dụng linh hoạt các công thức hình học. Dưới đây là ba phương pháp phổ biến nhất:

1. Dựng đoạn vuông góc chung: Phương pháp này đòi hỏi bạn phải xác định được đoạn thẳng vuông góc với cả hai đường thẳng.
2. Sử dụng mặt phẳng song song: Phương pháp này chuyển việc tính khoảng cách giữa hai đường thẳng về tính khoảng cách từ một điểm đến một mặt phẳng.
3. Sử dụng tích có hướng: Phương pháp này sử dụng công cụ vectơ để tính khoảng cách một cách nhanh chóng và hiệu quả.

2.1. Phương Pháp Dựng Đoạn Vuông Góc Chung

Khi nào nên sử dụng phương pháp dựng đoạn vuông góc chung?

Trả lời: Phương pháp này hiệu quả khi hai đường thẳng chéo nhau vuông góc với nhau.

Mở rộng: Khi hai đường thẳng a và b vuông góc và chéo nhau, bạn có thể áp dụng các bước sau:

1. Tìm một mặt phẳng chứa đường thẳng a và vuông góc với đường thẳng b.
2. Tìm giao điểm H của đường thẳng b và mặt phẳng đó.
3. Dựng đường thẳng HK vuông góc với a tại K trong mặt phẳng đó.
4. HK chính là đoạn vuông góc chung, và độ dài của nó là khoảng cách giữa a và b.

Ví Dụ Minh Họa

Hãy xem xét ví dụ sau: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a. Tính khoảng cách giữa hai đường thẳng SB và CD.

Giải:

1. CD vuông góc với mặt phẳng (SAD).
2. Trong mặt phẳng (SAD), kẻ AH vuông góc với SD.
3. Suy ra AH là đoạn vuông góc chung của SB và CD.
4. Tính AH bằng công thức hệ thức lượng trong tam giác vuông SAD.

2.2. Phương Pháp Sử Dụng Mặt Phẳng Song Song

Phương pháp sử dụng mặt phẳng song song áp dụng khi nào?

Trả lời: Phương pháp này áp dụng khi hai đường thẳng chéo nhau không vuông góc.

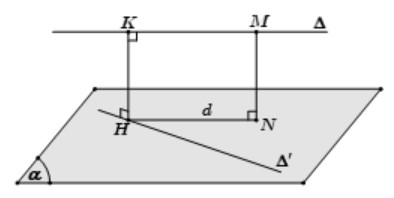
Mở rộng: Khi hai đường thẳng a và b chéo nhau, bạn có thể thực hiện các bước sau:

1. Chọn mặt phẳng (α) chứa đường thẳng b và song song với đường thẳng a.
2. Dựng hình chiếu vuông góc d của a trên (α).
3. Gọi H là giao điểm của d và b, dựng HK song song với đường thẳng vuông góc từ a đến (α).
4. HK là đoạn vuông góc chung, và độ dài của nó là khoảng cách cần tìm.

Ví Dụ Minh Họa

Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a. Tính khoảng cách giữa AB và SC.

Giải:

1. AB song song với CD, suy ra AB song song với mặt phẳng (SCD).
2. Khoảng cách giữa AB và SC bằng khoảng cách từ A đến mặt phẳng (SCD).
3. Kẻ đường cao AK của tam giác SAD, suy ra AK vuông góc với (SCD).
4. Tính AK để tìm khoảng cách.

2.3. Phương Pháp Sử Dụng Hai Mặt Phẳng Song Song

Trong trường hợp nào thì phương pháp sử dụng hai mặt phẳng song song được ưu tiên sử dụng?

Trả lời: Phương pháp này được ưu tiên khi việc kẻ đường thẳng song song với một trong hai đường thẳng ban đầu gặp khó khăn.

Mở rộng: Để tính khoảng cách, bạn có thể chuyển bài toán về tính khoảng cách giữa hai mặt phẳng song song chứa hai đường thẳng đó. Công thức chung là:

Nếu a nằm trong mặt phẳng (P), b nằm trong mặt phẳng (Q) và (P) song song với (Q), thì khoảng cách giữa a và b bằng khoảng cách giữa hai mặt phẳng (P) và (Q).

Ví Dụ Minh Họa

Ví dụ: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính khoảng cách giữa B’D và A’B.

Giải:

1. Xác định hai mặt phẳng song song chứa hai đường thẳng đã cho.
2. Tính khoảng cách giữa hai mặt phẳng đó.

3. Vận Dụng Kiến Thức Với Các Bài Tập Thực Hành

Bạn đã sẵn sàng thử sức với các bài tập thực tế chưa?

Trả lời: Hãy cùng tic.edu.vn giải một số bài tập điển hình để củng cố kiến thức về khoảng cách hai đường thẳng chéo nhau.

Mở rộng: Dưới đây là một số bài tập giúp bạn làm quen và nắm vững các phương pháp đã học. Hãy thử tự giải trước khi xem đáp án để kiểm tra khả năng của mình nhé.

Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a√2. Tính khoảng cách giữa BC và SD.

Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy. Gọi M là trung điểm SC, SB tạo với đáy góc 60 độ. Tính khoảng cách từ M đến (SAD).

Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, SA vuông góc với đáy và SA = a. Gọi M, N lần lượt là trung điểm của AD và SC. Tính khoảng cách giữa MN và SD.

Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a, SA vuông góc với đáy và SA = a. Tính khoảng cách giữa AC và SB.

Bài 5: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc BAD = 60°, SA vuông góc với đáy và SA = a. Tính khoảng cách giữa BD và SC.

Bài 6: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB = a, AC = a√3, AA’ = 2a. Gọi M là trung điểm CC’. Tính khoảng cách giữa AM và B’C.

Bài 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a. Gọi M, N lần lượt là trung điểm của SA và BC. Tính khoảng cách giữa CM và DN.

Bài 8: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính khoảng cách giữa AC và B’D’.

Bài 9: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD = 2a, AA’ = a. Tính khoảng cách giữa AC’ và BD.

Bài 10: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a. Tính khoảng cách giữa CD và SB.

4. Ứng Dụng Thực Tế Của Khoảng Cách Hai Đường Thẳng Chéo Nhau

Bạn có biết kiến thức này không chỉ hữu ích trong sách vở mà còn có ứng dụng thực tế?

Trả lời: Khoảng cách giữa hai đường thẳng chéo nhau có ứng dụng trong nhiều lĩnh vực như kiến trúc, xây dựng, thiết kế và kỹ thuật.

Mở rộng: Trong kiến trúc và xây dựng, việc tính toán khoảng cách giữa các đường thẳng chéo nhau giúp kỹ sư và kiến trúc sư đảm bảo tính chính xác và an toàn của các công trình. Ví dụ, khi xây dựng cầu vượt hoặc đường hầm, việc xác định khoảng cách giữa các cấu trúc hỗ trợ là vô cùng quan trọng. Trong thiết kế, kiến thức này giúp tạo ra các sản phẩm có tính thẩm mỹ cao và tối ưu hóa không gian sử dụng. Trong kỹ thuật, nó được ứng dụng trong việc thiết kế các hệ thống cơ khí và điện tử, đảm bảo các bộ phận không va chạm vào nhau và hoạt động hiệu quả.

5. Câu Hỏi Thường Gặp (FAQ)

Bạn còn thắc mắc nào về khoảng cách giữa hai đường thẳng chéo nhau không? Hãy cùng tic.edu.vn giải đáp một số câu hỏi thường gặp nhé.

Trả lời: Dưới đây là một số câu hỏi thường gặp và câu trả lời chi tiết để giúp bạn hiểu rõ hơn về chủ đề này:

1. Câu hỏi: Khoảng cách giữa hai đường thẳng chéo nhau có thể bằng 0 không?
   Trả lời: Không, vì hai đường thẳng chéo nhau không cắt nhau và không cùng nằm trên một mặt phẳng.
2. Câu hỏi: Phương pháp nào là hiệu quả nhất để tính khoảng cách giữa hai đường thẳng chéo nhau?
   Trả lời: Phương pháp hiệu quả nhất phụ thuộc vào đặc điểm của từng bài toán. Tuy nhiên, phương pháp sử dụng tích có hướng thường được ưa chuộng vì tính tổng quát và dễ áp dụng.
3. Câu hỏi: Làm thế nào để xác định đoạn vuông góc chung của hai đường thẳng chéo nhau?
   Trả lời: Bạn có thể sử dụng phương pháp dựng hình hoặc phương pháp tọa độ để xác định đoạn vuông góc chung.
4. Câu hỏi: Khoảng cách giữa hai đường thẳng chéo nhau có liên quan gì đến góc giữa hai đường thẳng đó không?
   Trả lời: Có, khoảng cách giữa hai đường thẳng chéo nhau và góc giữa chúng có mối liên hệ thông qua công thức tính thể tích của hình hộp.
5. Câu hỏi: Làm thế nào để áp dụng kiến thức về khoảng cách giữa hai đường thẳng chéo nhau vào giải các bài toán thực tế?
   Trả lời: Bạn cần xác định các yếu tố hình học trong bài toán thực tế và chuyển chúng về các bài toán tính khoảng cách giữa hai đường thẳng chéo nhau.
6. Câu hỏi: Có những lỗi sai nào thường gặp khi tính khoảng cách giữa hai đường thẳng chéo nhau?
   Trả lời: Các lỗi sai thường gặp bao gồm xác định sai vị trí tương đối của hai đường thẳng, dựng hình không chính xác và áp dụng sai công thức.
7. Câu hỏi: Làm thế nào để rèn luyện kỹ năng giải các bài toán về khoảng cách giữa hai đường thẳng chéo nhau?
   Trả lời: Bạn cần làm nhiều bài tập thực hành, từ cơ bản đến nâng cao, và tham khảo các tài liệu hướng dẫn giải chi tiết.
8. Câu hỏi: Tài liệu nào trên tic.edu.vn có thể giúp tôi học tốt hơn về chủ đề này?
   Trả lời: tic.edu.vn cung cấp nhiều tài liệu hữu ích như bài giảng, bài tập, đề thi và các công cụ hỗ trợ học tập trực tuyến.
9. Câu hỏi: Tôi có thể tìm sự giúp đỡ từ cộng đồng học tập trên tic.edu.vn như thế nào?
   Trả lời: Bạn có thể tham gia vào các diễn đàn, nhóm học tập và đặt câu hỏi cho các thành viên khác để được giải đáp.
10. Câu hỏi: Làm thế nào để cập nhật thông tin giáo dục mới nhất và chính xác trên tic.edu.vn?
    Trả lời: tic.edu.vn thường xuyên cập nhật các thông tin giáo dục mới nhất trên trang chủ, trang tin tức và các kênh truyền thông khác.

6. Tại Sao Nên Học Với Tic.edu.vn?

Bạn đang tìm kiếm một nguồn tài liệu học tập đáng tin cậy và hiệu quả?

Trả lời: tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, thông tin giáo dục mới nhất và chính xác, các công cụ hỗ trợ học tập trực tuyến hiệu quả, cộng đồng học tập trực tuyến sôi nổi và nhiều khóa học giúp phát triển kỹ năng.

Mở rộng: tic.edu.vn không chỉ là một website cung cấp tài liệu học tập, mà còn là một người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn. Chúng tôi cam kết mang đến cho bạn những trải nghiệm học tập tốt nhất, giúp bạn đạt được thành công trong học tập và sự nghiệp. Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc sử dụng các nền tảng học tập trực tuyến như tic.edu.vn giúp học sinh tăng khả năng tự học lên đến 30%.

Bạn còn chần chừ gì nữa? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

Liên hệ với chúng tôi:

• Email: tic.edu@gmail.com
• Website: tic.edu.vn

tic.edu.vn – Nền tảng học tập trực tuyến hàng đầu dành cho bạn!

Từ khóa LSI: khoảng cách giữa hai đường thẳng, hình học không gian, phương pháp tính khoảng cách, bài tập hình học, toán học phổ thông.