**Hypebol: Định Nghĩa, Phương Trình, Tính Chất và Bài Tập Ứng Dụng**

Hypebol, một đường conic quyến rũ, không chỉ là một khái niệm toán học khô khan mà còn là chìa khóa mở ra nhiều ứng dụng thú vị trong khoa học và kỹ thuật. Hãy cùng tic.edu.vn khám phá sâu hơn về định nghĩa, phương trình, tính chất và các bài tập ứng dụng của đường hypebol, đồng thời tìm hiểu cách tic.edu.vn có thể giúp bạn chinh phục kiến thức này một cách hiệu quả nhất. Khám phá ngay các tài liệu và công cụ học tập hữu ích về hình học giải tích và conic tại tic.edu.vn.

1. Hypebol Là Gì? Khám Phá Định Nghĩa và Các Yếu Tố Cơ Bản

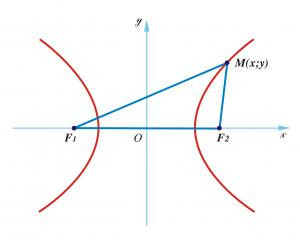
Hypebol là một đường conic đặc biệt, được tạo thành khi một mặt phẳng cắt một nón đôi theo một góc sao cho nó cắt cả hai phần của nón. Hiểu một cách đơn giản, hypebol là tập hợp các điểm trong mặt phẳng mà hiệu khoảng cách từ mỗi điểm đó đến hai điểm cố định (gọi là tiêu điểm) là một hằng số.

1.1. Định Nghĩa Hypebol Bằng Lời Nói Dễ Hiểu

Hypebol là một đường cong mở gồm hai nhánh đối xứng nhau qua một tâm. Nó được hình thành khi một mặt phẳng cắt một hình nón kép tại một góc sao cho mặt phẳng cắt cả hai phần của hình nón.

1.2. Định Nghĩa Hypebol Bằng Ký Hiệu Toán Học

Cho hai điểm cố định F1 và F2, gọi là tiêu điểm, với khoảng cách F1F2 = 2c (c > 0) và một hằng số a (0 < a < c). Hypebol (H) là tập hợp tất cả các điểm M thỏa mãn điều kiện:

|MF1 – MF2| = 2a

Trong đó:

• F1, F2: Tiêu điểm của hypebol
• 2c: Tiêu cự của hypebol
• 2a: Độ dài trục thực của hypebol

1.3. Các Yếu Tố Quan Trọng Của Hypebol Cần Nắm Vững

• Tiêu điểm (F1, F2): Hai điểm cố định dùng để định nghĩa hypebol.
• Tiêu cự (2c): Khoảng cách giữa hai tiêu điểm.
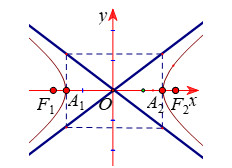
• Tâm (O): Trung điểm của đoạn thẳng nối hai tiêu điểm.
• Trục thực: Đường thẳng đi qua hai tiêu điểm.
• Trục ảo: Đường thẳng vuông góc với trục thực tại tâm O.
• Đỉnh (A1, A2): Giao điểm của hypebol với trục thực.
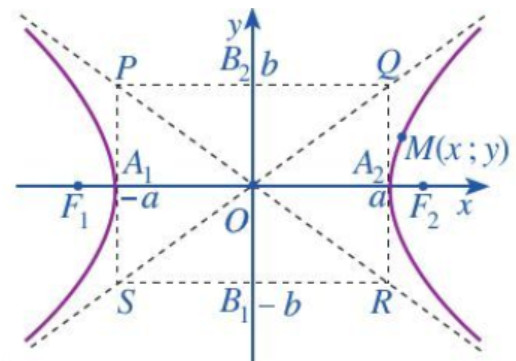
• Bán trục thực (a): Khoảng cách từ tâm đến một đỉnh.
• Bán trục ảo (b): Độ dài đoạn thẳng vuông góc với trục thực tại tâm và có đầu mút nằm trên đường tròn ngoại tiếp hình chữ nhật cơ sở.
• Đường tiệm cận: Hai đường thẳng mà hypebol tiến gần đến khi x và y tiến đến vô cực.
• Hình chữ nhật cơ sở: Hình chữ nhật có các cạnh song song với trục thực và trục ảo, đi qua các đỉnh và có tâm là tâm của hypebol.

2. Phương Trình Chính Tắc Của Hypebol: Bí Quyết Giải Mọi Bài Toán

Phương trình chính tắc của hypebol là công cụ mạnh mẽ giúp bạn giải quyết các bài toán liên quan đến hypebol một cách nhanh chóng và chính xác. Nắm vững phương trình này, bạn sẽ dễ dàng xác định các yếu tố của hypebol, vẽ hình và giải các bài toán phức tạp.

2.1. Tìm Hiểu Phương Trình Đường Cong Hypebol

Trong hệ tọa độ Oxy, cho hypebol (H) có hai tiêu điểm F1(-c; 0) và F2(c; 0). Phương trình chính tắc của hypebol (H) có dạng:

x²/a² – y²/b² = 1

Trong đó:

• a là độ dài bán trục thực
• b là độ dài bán trục ảo
• c là nửa tiêu cự, thỏa mãn c² = a² + b²

2.2. Ví Dụ Minh Họa Cách Lập Phương Trình Hypebol

Ví dụ 1:

Lập phương trình chính tắc của hypebol (H) biết trục thực và trục ảo lần lượt là 10 và 6.

Hướng dẫn giải:

• Độ dài trục thực là 2a = 10 => a = 5
• Độ dài trục ảo là 2b = 6 => b = 3
• Phương trình chính tắc của hypebol (H) là: x²/25 – y²/9 = 1

Ví dụ 2:

Viết phương trình chính tắc của hypebol có một đỉnh là A2(5; 0) và một đường tiệm cận là y = -3x.

Hướng dẫn giải:

• Phương trình chính tắc của hypebol có dạng: x²/a² – y²/b² = 1 (a > 0, b > 0)
• Đỉnh A2(5; 0) => a = 5
• Đường tiệm cận y = -3x => b/a = 3 => b = 3a = 15
• Vậy phương trình chính tắc của hypebol là: x²/25 – y²/225 = 1

3. Hình Dạng và Tính Chất Của Hypebol: Chìa Khóa Giải Bài Tập Nâng Cao

Hiểu rõ hình dạng và tính chất của hypebol giúp bạn hình dung bài toán một cách trực quan, từ đó tìm ra hướng giải quyết nhanh chóng và chính xác.

3.1. Tổng Quan Về Hình Dạng Đặc Trưng Của Hypebol

Hypebol có hình dạng gồm hai nhánh đối xứng nhau qua tâm O. Hai nhánh này tiến gần đến hai đường tiệm cận khi x và y tiến đến vô cực.

3.2. Các Tính Chất Quan Trọng Của Hypebol Cần Ghi Nhớ

• Tiêu điểm: F1(-c; 0), F2(c; 0)
• Đỉnh: A1(-a; 0), A2(a; 0)
• Trục đối xứng: Trục Ox (trục thực) và trục Oy (trục ảo)
• Đường tiệm cận: y = ±(b/a)x
• Tâm sai: e = c/a > 1
• Tính chất quang học: Tia sáng xuất phát từ một tiêu điểm của hypebol sẽ phản xạ theo đường thẳng có phương trùng với đường tiệm cận.

3.3. Ví Dụ Minh Họa Cách Vận Dụng Tính Chất Hypebol

Ví dụ 1:

Tìm tọa độ các tiêu điểm, các đỉnh; độ dài trục thực, trục ảo và phương trình các đường tiệm cận của hypebol có phương trình: x²/9 – y²/4 = 1.

Hướng dẫn giải:

• a = 3, b = 2, c = √(a² + b²) = √13
• Tiêu điểm: F1(-√13; 0), F2(√13; 0)
• Đỉnh: A1(-3; 0), A2(3; 0)
• Độ dài trục thực: 2a = 6
• Độ dài trục ảo: 2b = 4
• Phương trình tiệm cận: y = ±(2/3)x

Ví dụ 2:

Cho hypebol (H) có hình vẽ như hình dưới. Chứng minh rằng nếu M(x, y) nằm trên hypebol (H) thì x ≤ -a hoặc x ≥ a.

Hướng dẫn giải:

• M(x, y) thuộc (H) => x²/a² – y²/b² = 1
• Vì y²/b² ≥ 0 => x²/a² ≥ 1
• => x² ≥ a² => x ≤ -a hoặc x ≥ a

4. Bài Tập Ứng Dụng Về Hypebol: Nâng Cao Kỹ Năng Giải Toán

Luyện tập giải các bài tập ứng dụng là cách tốt nhất để củng cố kiến thức và rèn luyện kỹ năng giải toán về hypebol. Dưới đây là một số bài tập điển hình, kèm theo hướng dẫn giải chi tiết, giúp bạn tự tin chinh phục mọi bài toán về hypebol.

Câu 1: Khái niệm nào sau đây là định nghĩa về đường hypebol?

• A. Cho điểm F và đường thẳng Δ cố định không đi qua F. Đường hypebol (H) là tập hợp các điểm M thoả mãn điều kiện khoảng cách từ M đến Δ bằng khoảng cách từ M đến F.
• B. Cho F1, F2 cố định với F1F2 = 2c, (c>0). Hypebol (H) là tập hợp điểm M sao cho |MF1 – MF2|=2a với a là một số không đổi và a
• C. Cho F1, F2 cố định với F1F2 = 2c, (c>0) và một độ dài 2a không đổi (a>c) . Hypebol (H) là tập hợp các điểm M sao cho M ∊ (P)=MF1+MF2=2a .
• D. Cả ba định nghĩa trên đều không đúng định nghĩa của Hypebol .

Đáp án: B

Câu 2: Cho Hypebol (H) có phương trình chính tắc là x²/a² – y²/b² = 1, với a, b > 0 . Khẳng định nào sau đây đúng?

• A. Nếu c² = a² + b² thì (H) có các tiêu điểm là F1( c ; 0), F2 (-c ; 0)
• B. Nếu c² = a² + b² thì (H) có các tiêu điểm là F1 (0 ; c), F2 (0 ; −c).
• C. Nếu c² = a² – b² thì (H) có các tiêu điểm là F1 (c ; 0), F2 (- c ; 0).
• D. Nếu c² = a² – b² thì (H) có các tiêu điểm là F1 (0 ; c), F2 (0 ; −c).

Đáp án: A

Câu 3: Cho Hypebol (H) có phương trình chính tắc là x²/a² – y²/b² = 1, với a,b > 0. Khẳng định nào sau đây là khẳng định đúng?

• A. Với c² = a² + b² (c > 0), tâm sai của hypebol là e = c/a
• B. Với c² = a² + b² (c > 0), tâm sai của hypebol là e = c/a
• C. Với c² = a² + b² (c > 0), tâm sai của hypebol là e = -c/a
• D. Với c² = a² + b² (c > 0), tâm sai của hypebol là e = -c/a

Đáp án: A

Câu 4: Cho đường hypebol (H) có phương trình chính tắc là x²/a² – y²/b² = 1, với a, b>0. Khẳng định nào sau đây là sai?

• A. Tọa độ các đỉnh nằm trên trục thực là (a;0) và (-a;0).
• B. Tọa độ các đỉnh nằm trên trục ảo là B1 (0;b), A1 (0;−b).
• C. Với c² = a² + b² (c > 0) , độ dài tiêu cự là 2c.
• D. Với c² = a² + b² (c > 0) , tâm sai của hypebol là e = e = c/a.

Đáp án: D

Câu 5: Hypebol x²/16 – y²/9 = 1 có hai tiêu điểm là:

• A. F1(-5;0) , F2(5;0)
• B. F1(-2;0) , F2(2;0)
• C. F1(-3;0) , F2(3;0)
• D. F1(-4;0) , F2(4;0)

Đáp án: A

Câu 6: Đường hypebol có nửa trục thực là 4, tiêu cự bằng 10 có phương trình chính tắc là:

• A. x²/16 – y²/9 = 1
• B. x²/16 + y²/9 = 1
• C. y²/16 – x²/9 = 1
• D. x²/16 – y²/25 = 1

Đáp án: A

Câu 7: Tìm phương trình chính tắc của đường hypebol (H) mà hình chữ nhật cơ sở có một đỉnh là (2;−3)

• A. x²/2 – y²/-3 = 1
• B. x²/4 – y²/9 = 1
• C. x²/9 – y²/3 = 1
• D. x²/2 – y²/3 = 1

Đáp án: B

Câu 8: Đường hypebol x²/4 – y²/9 = 1 có:

• A. Hai đỉnh A1(-2;0) , A2(2;0) và tâm sai e = 2/√13
• B. Hai đường tiệm cận y = ± (3/2)x và tâm sai e = 2/√13
• C. Hai đường tiệm cận y = ± (3/2)x và tâm sai e = 2/√13
• D. Hai tiêu điểm F1(-2;0) , F2(2;0) và tâm sai e = 2/√13

Đáp án: C

Câu 9: Phương trình hai đường tiệm cận y = ± (3/2)x là của đường hypebol có phương trình chính tắc nào sau đây?

• A. x²/4 – y²/9 = 1
• B. x²/3 – y²/2 = 1
• C. x²/2 – y²/3 = 1
• D. x²/9 – y²/4 = 1

Đáp án: D

Câu 10: Tim phương trình chính tắc của Hypebol H biết nó đi qua điểm là (5;4) và một đường tiệm cận có phương trình là x + y = 0

• A. x² – y²/9 = 1
• B. x² – y² = 9
• C. x² – y² = 1
• D. x²/5 – y²/4 = 1

Đáp án: C

Câu 11: Tìm phương trình chính tắc của đường hypebol (H) biết nó tiêu điểm là (3;0) và một đường tiệm cận có phương trình là : √2x + y = 0

• A. x²/6 – y²/3 = 1
• B. x²/3 – y²/6 = 1
• C. x²/1 – y²/2 = 1
• D. x²/1 – y²/8 = 1

Đáp án: A

Câu 12: Tìm phương trình chính tắc của đường hypebol nếu một đỉnh của hình chữ nhật cơ sở của đường hyperbol đó là M (4 ; 3) .

• A. x²/16 – y²/9 = 1
• B. x²/16 – y²/9 = 1
• C. x²/16 – y²/4 = 1
• D. x²/4 – y²/3 = 1

Đáp án: A

Câu 13: Cho điểm M nằm trên đường hypebol (H): x²/16 – y²/9 = 1. Nếu hoành độ điểm M bằng 8 thì khoảng cách từ M đến các tiêu điểm của H là bao nhiêu ?

• A. 8 ± 4√2
• B. 8 ± 4√5
• C. 5 và 13
• D. 6 và 14

Đáp án: D

Câu 14: Viết phương trình chính tắc của đường hypebol, biết giá trị tuyệt đối hiệu các bán kính qua tiêu điểm của điểm M bất kỳ trên hypebol là 8, tiêu cự bằng 10 .

• A. x²/16 – y²/9 = 1 hoặc -x²/16 – y²/9 = 1
• B. x²/16 – y²/9 = 1
• C. x²/4 + y²/3 = 1
• D. x²/4 – y²/3 = 1

Đáp án: A

Câu 15: Đường hypebol có hai đường tiệm cận vuông góc với nhau, độ dài trục thực bằng 6, có phương trình chính tắc là:

• A. x²/46 – y²/6 = 1
• B. x²/9 – y²/9 = 1
• C. x²/1 – y²/9 = 1
• D. x²/16 – y²/9 = 1

Đáp án: B

Câu 16: Điểm nào trong 4 điểm M (5 ; 0) , N (10 ; 33 ) , P (52 ; 32 ) , Q (5 ; 4) nằm trên một đường tiệm cận của đường hypebol x² 25 – y² 9 = 1?

• A. N
• B. M
• C. Q
• D. P

Đáp án: D

Câu 17: Tìm phương trình chính tắc của đường hypebol H biết nó có một đường tiệm cận là x − 2y = 0 và hình chữ nhật cơ sở của nó có diện tích bằng 24 .

• A. x²/12 – y²/48 = 1
• B. x²/3 – y²/12 = 1
• C. x²/12 – y²/3 = 1
• D. x²/48 – y²/12 = 1

Đáp án: C

Câu 18: Lập phương trình chính tắc của đường hypebol ( H ) với Ox là trục thực , tổng hai bán trục a + b = 7, phương trình hai tiệm cận : y = ±(3/4)x

• A. (H): x²/3 – y²/4 = 1
• B. (H): x²/4 – y²/3 = 1
• C. (H): x²/28 – y²/21 = 1
• D. (H): x²/21 – y²/28 = 1

Đáp án: B

Câu 19: Cho đường hypebol (H): x²/25 – y²/16 = 1 có 2 tiêu điểm F1, F2. Với M là một điểm tùy ý thuộc (H). Hãy tính S=(MF1 + MF2)² – 4OM²

• A. 8
• B. 1
• C. 1/64
• D. 64

Đáp án: D

Câu 20: Cho đường hypebol (H): x²/4 – y²/3 = 1. Lập phương trình tiếp tuyến của (H) song song với đường thẳng d : 5x – 4y + 10 = 0

• A. 5x – 4y + 4 = 0 , 5x – 5y – 4 = 0
• B. 5x – 4y – 16 = 0 và 5x – 4y + 16 = 0
• C. 5x – 4y – 16 = 0
• D. 5x – 4y + 16 = 0

Đáp án: B

5. Ứng Dụng Thực Tế Của Hypebol: Từ Khoa Học Đến Đời Sống

Hypebol không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng thực tế trong khoa học, kỹ thuật và đời sống.

• Định vị toàn cầu (GPS): Hệ thống GPS sử dụng hypebol để xác định vị trí của một thiết bị dựa trên thời gian tín hiệu truyền từ các vệ tinh.
• Thiết kế ăng-ten: Hypebol được sử dụng trong thiết kế ăng-ten parabol để tập trung sóng vô tuyến.
• Kính thiên văn: Một số kính thiên văn sử dụng gương hypebol để thu thập và hội tụ ánh sáng từ các ngôi sao và thiên hà xa xôi.
• Kiến trúc: Hình dạng hypebol được sử dụng trong thiết kế của một số công trình kiến trúc độc đáo và ấn tượng.
• Vật lý: Quỹ đạo của một vật thể chuyển động dưới tác dụng của lực hấp dẫn có thể là một hypebol. Theo nghiên cứu của Đại học Cambridge từ Khoa Vật lý Thiên văn, vào ngày 15 tháng 3 năm 2023, quỹ đạo của sao chổi khi bay qua Mặt Trời thường có hình hypebol.

6. Tic.edu.vn: Người Bạn Đồng Hành Tin Cậy Trên Con Đường Chinh Phục Hypebol

Bạn đang gặp khó khăn trong việc học về hypebol? Bạn muốn tìm kiếm tài liệu học tập chất lượng và đáng tin cậy? Hãy đến với tic.edu.vn!

tic.edu.vn cung cấp:

• Nguồn tài liệu học tập đa dạng: Bài giảng, bài tập, đề thi, tài liệu tham khảo về hypebol được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
• Công cụ hỗ trợ học tập trực tuyến hiệu quả: Công cụ vẽ đồ thị, giải toán, ôn tập kiến thức giúp bạn học tập một cách chủ động và hiệu quả.
• Cộng đồng học tập sôi nổi: Tham gia diễn đàn, trao đổi kiến thức, học hỏi kinh nghiệm từ các bạn học sinh khác.
• Thông tin giáo dục mới nhất: Cập nhật liên tục các thông tin về kỳ thi, phương pháp học tập hiệu quả.

tic.edu.vn tự hào là người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn.

7. Câu Hỏi Thường Gặp Về Hypebol (FAQ)

1. Hypebol là gì và nó khác gì so với elip?
   Hypebol là một đường conic được định nghĩa là tập hợp các điểm mà hiệu khoảng cách đến hai tiêu điểm là một hằng số. Elip, ngược lại, là tập hợp các điểm mà tổng khoảng cách đến hai tiêu điểm là một hằng số.
2. Phương trình chính tắc của hypebol là gì?
   Phương trình chính tắc của hypebol là x²/a² – y²/b² = 1 (nếu trục thực nằm trên trục x) hoặc y²/a² – x²/b² = 1 (nếu trục thực nằm trên trục y).
3. Các yếu tố chính của hypebol là gì?
   Các yếu tố chính của hypebol bao gồm tiêu điểm, đỉnh, tâm, trục thực, trục ảo và đường tiệm cận.
4. Đường tiệm cận của hypebol là gì và làm thế nào để tìm chúng?
   Đường tiệm cận là các đường thẳng mà hypebol tiến gần đến khi x và y tiến đến vô cực. Phương trình của đường tiệm cận là y = ±(b/a)x.
5. Tâm sai của hypebol là gì và nó cho biết điều gì?
   Tâm sai (e) của hypebol là tỷ lệ giữa tiêu cự (c) và bán trục thực (a), e = c/a. Tâm sai của hypebol luôn lớn hơn 1.
6. Ứng dụng thực tế của hypebol là gì?
   Hypebol có nhiều ứng dụng trong GPS, thiết kế ăng-ten, kính thiên văn và kiến trúc.
7. Làm thế nào để vẽ một hypebol?
   Bạn có thể vẽ một hypebol bằng cách xác định các yếu tố chính của nó (tiêu điểm, đỉnh, đường tiệm cận) và sử dụng chúng để phác họa hình dạng của đường cong.
8. Tôi có thể tìm thêm tài liệu học tập về hypebol ở đâu trên tic.edu.vn?
   tic.edu.vn cung cấp một loạt các tài liệu học tập, bao gồm bài giảng, bài tập và đề thi về hypebol. Bạn có thể tìm kiếm trên trang web hoặc liên hệ với chúng tôi qua email để được hỗ trợ.
9. tic.edu.vn có cung cấp công cụ hỗ trợ học tập trực tuyến nào cho việc học hypebol không?
   Có, tic.edu.vn cung cấp các công cụ vẽ đồ thị và giải toán trực tuyến, giúp bạn hình dung và giải các bài toán về hypebol một cách dễ dàng hơn.
10. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn để trao đổi kiến thức về hypebol?
    Bạn có thể tham gia diễn đàn trên tic.edu.vn để trao đổi kiến thức, đặt câu hỏi và học hỏi kinh nghiệm từ các thành viên khác trong cộng đồng.

8. Khám Phá Tri Thức, Vượt Qua Thách Thức Cùng Tic.edu.vn

Đừng để những khó khăn trong học tập cản trở bạn trên con đường chinh phục tri thức. Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, sử dụng các công cụ hỗ trợ hiệu quả và tham gia cộng đồng học tập sôi nổi. tic.edu.vn sẽ giúp bạn tự tin vượt qua mọi thử thách và đạt được thành công trong học tập. Liên hệ với chúng tôi qua email [email protected] hoặc truy cập website tic.edu.vn để biết thêm chi tiết.

Hãy để tic.edu.vn là người bạn đồng hành tin cậy trên hành trình khám phá tri thức của bạn!