**Hình Tứ Giác: Định Nghĩa, Phân Loại, Tính Chất và Bài Tập**

Hình Tứ Giác là một khái niệm quan trọng trong hình học, xuất hiện thường xuyên trong chương trình học và các bài toán ứng dụng. Hãy cùng tic.edu.vn khám phá định nghĩa, tính chất, phân loại và các dạng bài tập liên quan đến hình tứ giác để nắm vững kiến thức nền tảng này. Với sự đa dạng về tài liệu và công cụ hỗ trợ, tic.edu.vn sẽ là người bạn đồng hành tin cậy trên con đường chinh phục kiến thức.

1. Hình Tứ Giác Là Gì? Định Nghĩa và Ký Hiệu

Hình tứ giác là một đa giác có bốn đỉnh và bốn cạnh, trong đó không có bất kỳ hai đoạn thẳng nào cùng nằm trên một đường thẳng. Điều này có nghĩa là bốn điểm tạo thành hình tứ giác không được thẳng hàng.

• Phân loại: Tứ giác có thể là tứ giác lồi, tứ giác lõm hoặc tứ giác tự cắt (có cặp cạnh đối cắt nhau).
• Ký hiệu: Hình tứ giác được ký hiệu bằng bốn chữ cái in hoa, ví dụ: ABCD.
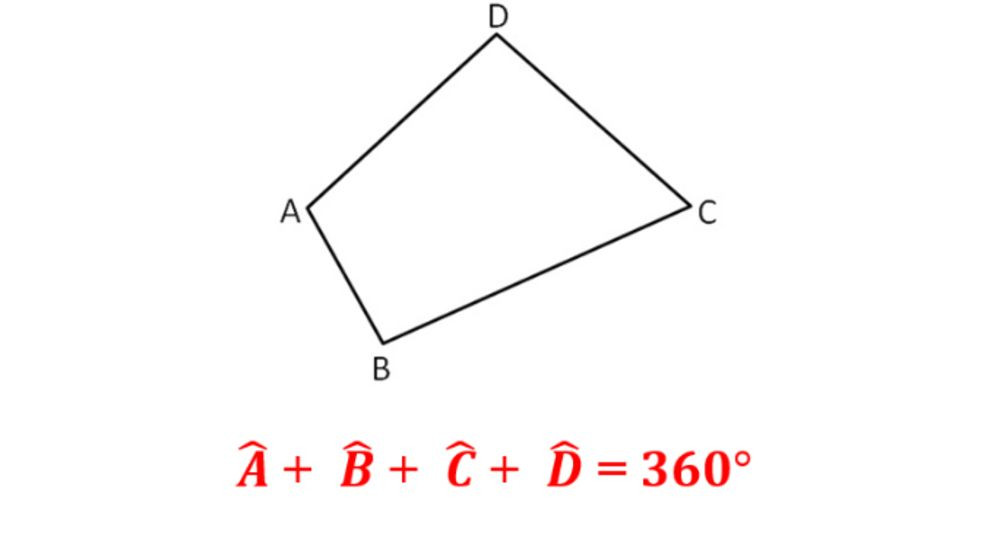
• Tổng các góc: Tổng các góc trong một hình tứ giác luôn bằng 360 độ: ∠A + ∠B + ∠C + ∠D = 360°. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, kiến thức về tổng các góc của hình tứ giác cung cấp nền tảng để giải quyết nhiều bài toán liên quan đến tính toán góc và chứng minh các tính chất hình học.

Alt: Hình tứ giác ABCD minh họa khái niệm cơ bản về hình học phẳng.

2. Khám Phá Tính Chất Quan Trọng Của Hình Tứ Giác

Để hiểu sâu hơn về hình tứ giác, chúng ta cần nắm vững các tính chất đặc trưng của nó.

2.1. Tính Chất Về Đường Chéo

Trong một hình tứ giác lồi, hai đường chéo sẽ giao nhau tại một điểm nằm bên trong tứ giác. Ngược lại, nếu hai đường chéo của một tứ giác giao nhau tại một điểm nằm bên trong tứ giác đó, thì tứ giác đó là tứ giác lồi.

2.2. Tính Chất Về Góc

Tổng số đo của bốn góc trong một hình tứ giác luôn bằng 360 độ. Tính chất này là nền tảng để giải quyết nhiều bài toán liên quan đến tính toán góc trong hình tứ giác.

Alt: Minh họa tổng bốn góc trong hình tứ giác luôn là 360 độ.

3. Phân Loại Hình Tứ Giác: Nhận Diện Các Dạng Cơ Bản

Hình tứ giác có thể được phân loại thành nhiều dạng khác nhau, mỗi dạng có những đặc điểm và tính chất riêng. Việc nhận biết và phân loại các dạng hình tứ giác là một kỹ năng quan trọng trong học tập và giải toán.

3.1. Tứ Giác Đơn

Tứ giác đơn là hình tứ giác mà không có cạnh nào cắt nhau. Nói cách khác, các cạnh của tứ giác không giao nhau tại bất kỳ điểm nào khác ngoài các đỉnh của nó.

3.2. Tứ Giác Lõm

Tứ giác lõm là hình tứ giác có ít nhất một góc lớn hơn 180 độ. Trong tứ giác lõm, có ít nhất một đường chéo nằm bên ngoài tứ giác.

3.3. Tứ Giác Lồi

Tứ giác lồi là hình tứ giác mà tất cả các góc đều nhỏ hơn 180 độ. Trong tứ giác lồi, cả hai đường chéo đều nằm bên trong tứ giác. Tứ giác lồi luôn nằm trong một nửa mặt phẳng chứa bất kỳ cạnh nào của nó.

3.4. Tứ Giác Không Đều

Tứ giác không đều là hình tứ giác mà không có cặp cạnh nào song song với nhau. Tứ giác không đều thường được sử dụng để đại diện cho dạng tứ giác lồi tổng quát.

Alt: Mô tả hình tứ giác lồi với các đặc điểm trực quan.

4. Các Dạng Hình Tứ Giác Đặc Biệt: Chi Tiết và Dấu Hiệu Nhận Biết

Ngoài các dạng tứ giác cơ bản, chúng ta còn có các dạng hình tứ giác đặc biệt với những tính chất và ứng dụng quan trọng.

4.1. Hình Thang

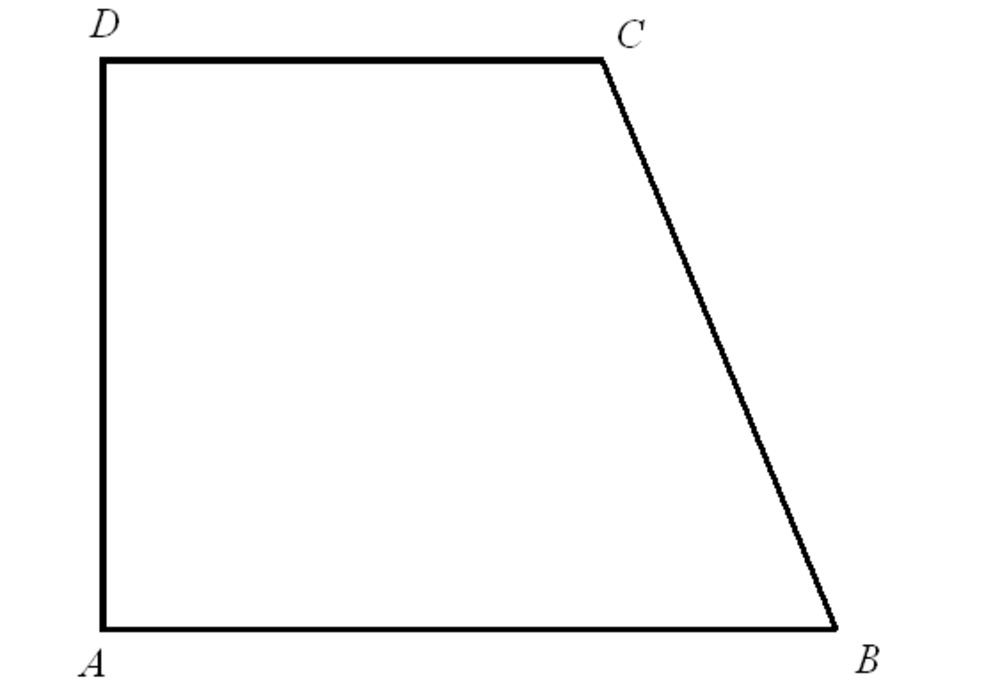
Hình thang là hình tứ giác có ít nhất một cặp cạnh đối song song. Hai cạnh song song này được gọi là cạnh đáy, hai cạnh còn lại gọi là cạnh bên.

Alt: Hình thang với hai cạnh đáy song song và các yếu tố hình học.

4.2. Hình Thang Cân

Hình thang cân là hình thang có hai góc kề cùng một cạnh đáy bằng nhau. Hình thang cân cũng có hai đường chéo bằng nhau.

• Đặc điểm nhận biết:
  • Là hình thang (có ít nhất 2 cạnh đối song song).
  • Có hai góc kề cùng một cạnh đáy bằng nhau.
  • Có hai đường chéo bằng nhau.

4.3. Hình Bình Hành

Hình bình hành là hình tứ giác có hai cặp cạnh đối song song. Hình bình hành có các tính chất sau:

• Các cạnh đối bằng nhau.
• Các góc đối bằng nhau.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
  Hình bình hành là một trường hợp đặc biệt của hình thang.

Alt: Hình bình hành với các cạnh đối song song và tính chất đường chéo.

4.4. Hình Thoi

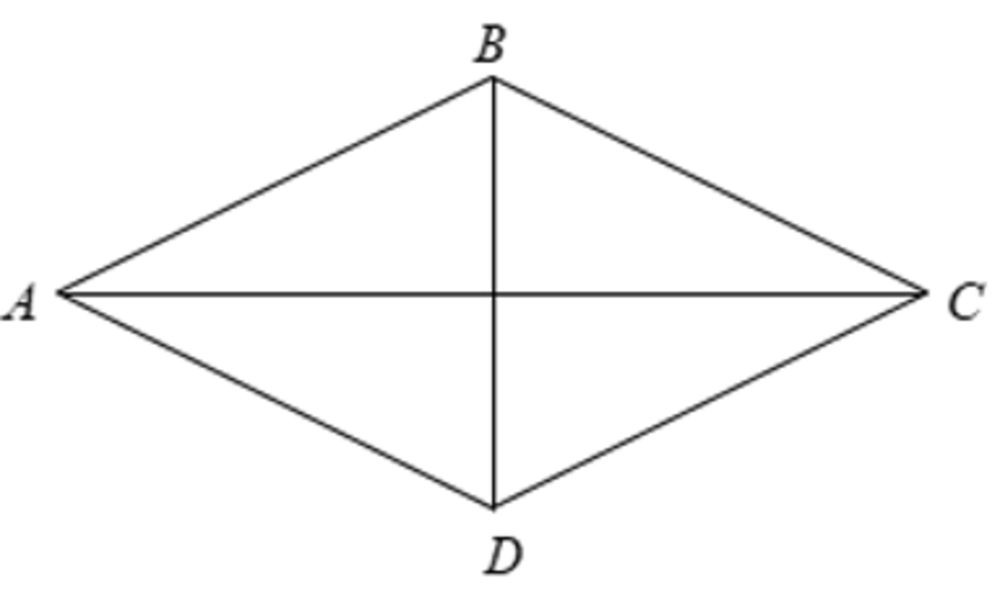
Hình thoi là hình tứ giác có bốn cạnh bằng nhau. Hình thoi có các tính chất sau:

• Hai đường chéo vuông góc với nhau.
• Hai đường chéo là đường phân giác của các góc của hình thoi.

Alt: Hình thoi với bốn cạnh bằng nhau và đường chéo vuông góc.

4.5. Hình Chữ Nhật

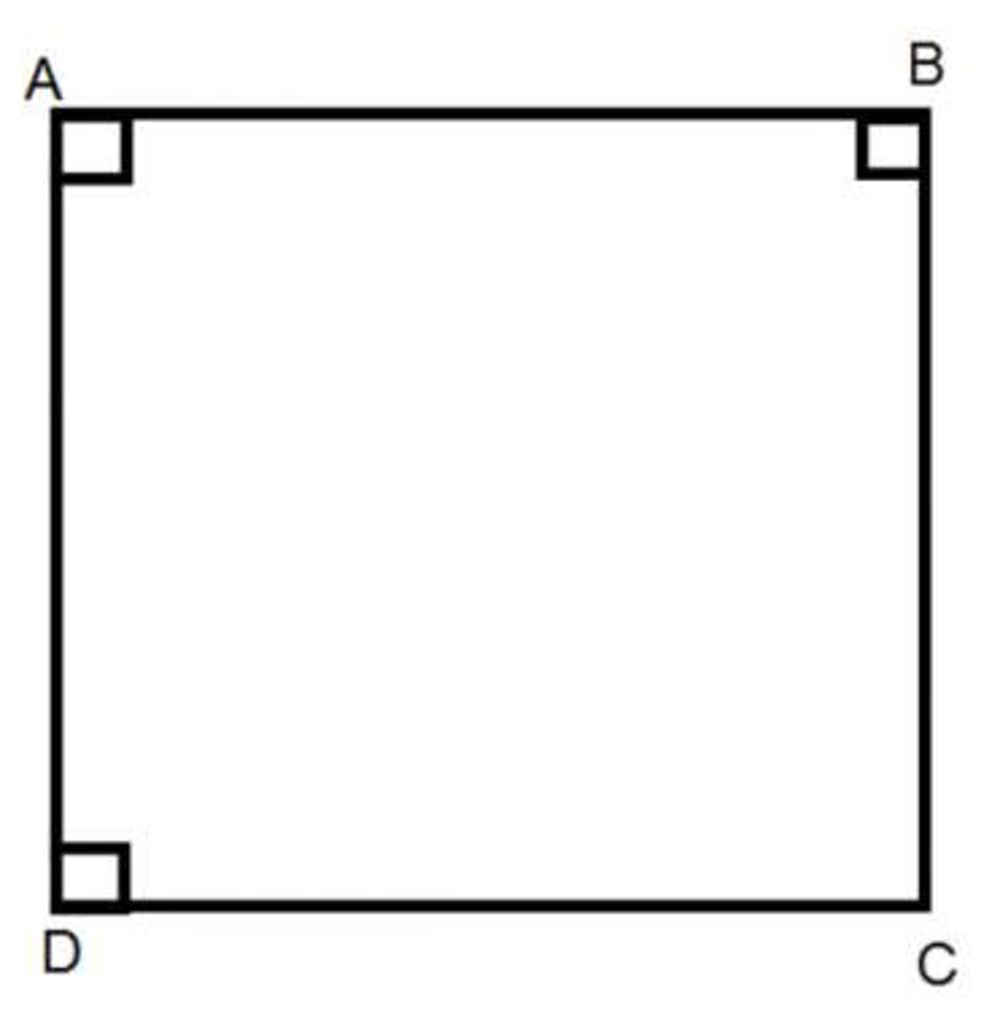
Hình chữ nhật là hình tứ giác có bốn góc vuông. Hình chữ nhật có các tính chất sau:

• Hai đường chéo bằng nhau.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Alt: Hình chữ nhật với bốn góc vuông và đường chéo bằng nhau.

4.6. Hình Vuông

Hình vuông là hình tứ giác có bốn góc vuông và bốn cạnh bằng nhau. Hình vuông là một trường hợp đặc biệt của cả hình thoi và hình chữ nhật. Hình vuông có tất cả các tính chất của hình thoi và hình chữ nhật.

Alt: Hình vuông với bốn góc vuông và bốn cạnh bằng nhau.

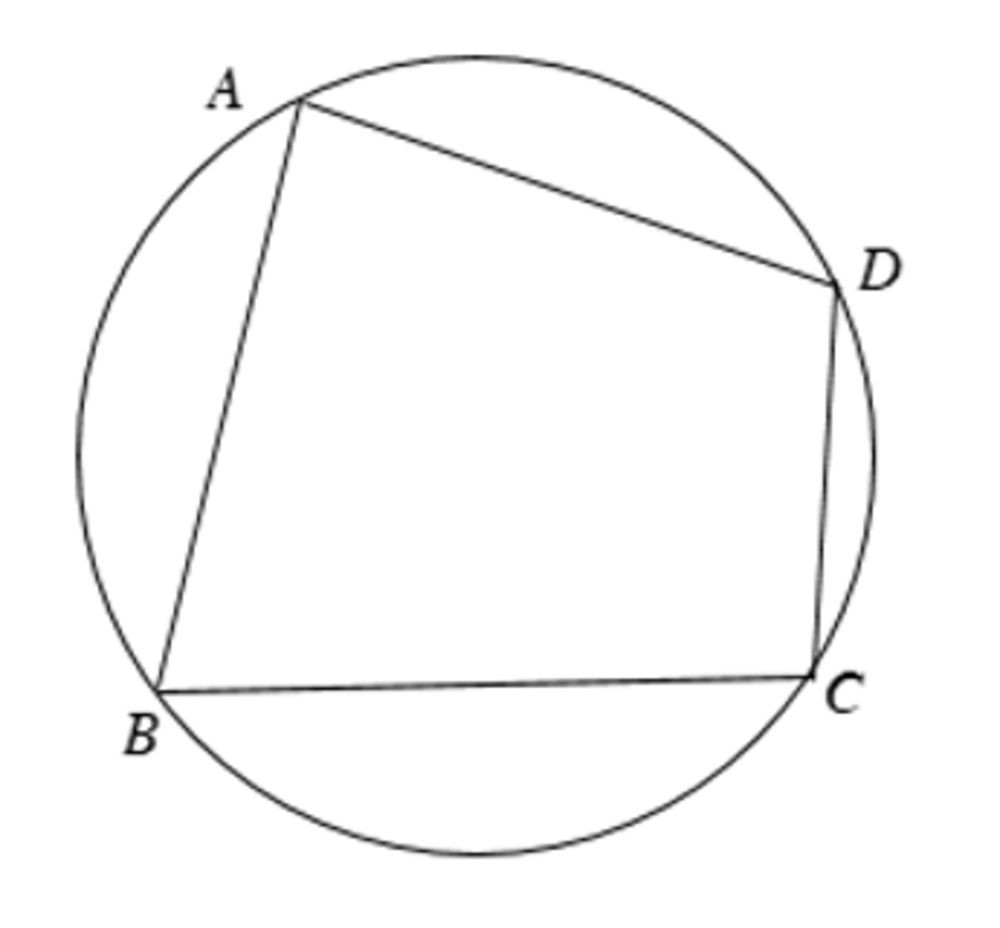
4.7. Tứ Giác Nội Tiếp

Tứ giác nội tiếp là hình tứ giác có bốn đỉnh nằm trên cùng một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp tứ giác. Tâm của đường tròn ngoại tiếp là tâm đường tròn ngoại tiếp, và bán kính của đường tròn là bán kính ngoại tiếp. Theo một nghiên cứu từ Đại học Quốc gia Hà Nội, Khoa Toán – Tin, vào ngày 20 tháng 4 năm 2023, tứ giác nội tiếp có ứng dụng quan trọng trong việc giải các bài toán liên quan đến đường tròn và góc.

Alt: Tứ giác nội tiếp và đường tròn ngoại tiếp đi qua bốn đỉnh.

5. Công Thức Tính Chu Vi và Diện Tích Hình Tứ Giác

Khi học về hình tứ giác, không thể bỏ qua các công thức tính chu vi và diện tích.

5.1. Công Thức Tính Chu Vi Tứ Giác

Chu vi của một hình tứ giác là tổng độ dài của bốn cạnh của nó.

P = a + b + c + d

Trong đó:

• P: là chu vi hình tứ giác
• a, b, c, d: là độ dài của bốn cạnh của tứ giác

Ví dụ: Cho hình tứ giác ABCD có độ dài các cạnh AB = a = 5cm, BC = b = 7cm, CD = c = 9cm, DA = d = 5cm. Tính chu vi hình tứ giác ABCD.

Lời giải:

Chu vi hình tứ giác ABCD là:

P = a + b + c + d = 5 + 7 + 9 + 5 = 26cm

Vậy chu vi hình tứ giác ABCD là 26cm.

5.2. Công Thức Tính Diện Tích Tứ Giác

Công thức tính diện tích tứ giác phụ thuộc vào dạng hình tứ giác đó là hình gì, không có công thức tính chung cho tất cả các loại tứ giác. Ví dụ:

• Hình vuông: S = a x a (S là diện tích hình vuông, a là độ dài cạnh hình vuông)
• Hình chữ nhật: S = a x b (S là diện tích hình chữ nhật, a là chiều dài hình chữ nhật, b là chiều rộng hình chữ nhật)
• Hình bình hành: S = a x h (S là diện tích hình bình hành, a là độ dài cạnh đáy hình bình hành, h là chiều cao hạ từ đỉnh xuống cạnh đáy hình bình hành)

6. Luyện Tập Các Dạng Toán Về Hình Tứ Giác

Để nắm vững kiến thức về hình tứ giác, hãy cùng luyện tập một số dạng bài tập thường gặp.

6.1. Dạng 1: Bài Tập Về Định Nghĩa và Công Thức

Dạng bài tập trắc nghiệm về định nghĩa, công thức và nhận dạng hình tứ giác giúp học sinh ghi nhớ kiến thức một cách hiệu quả.

Ví dụ: Hình tứ giác có 4 góc vuông, 4 cạnh bằng nhau, các cạnh đối song song là hình gì?

1. Hình chữ nhật
2. Hình thoi
3. Hình vuông
4. Hình bình hành

Đáp án: 3. Hình vuông

6.2. Dạng 2: Nhận Biết Các Dạng Hình Tứ Giác

Dạng bài tập này yêu cầu học sinh nhận biết các dạng hình tứ giác khác nhau thông qua các hình vẽ hoặc mô tả.

Ví dụ 1: Tìm hình tứ giác luôn nằm trong nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tam giác?

Đáp án: Tứ giác lồi

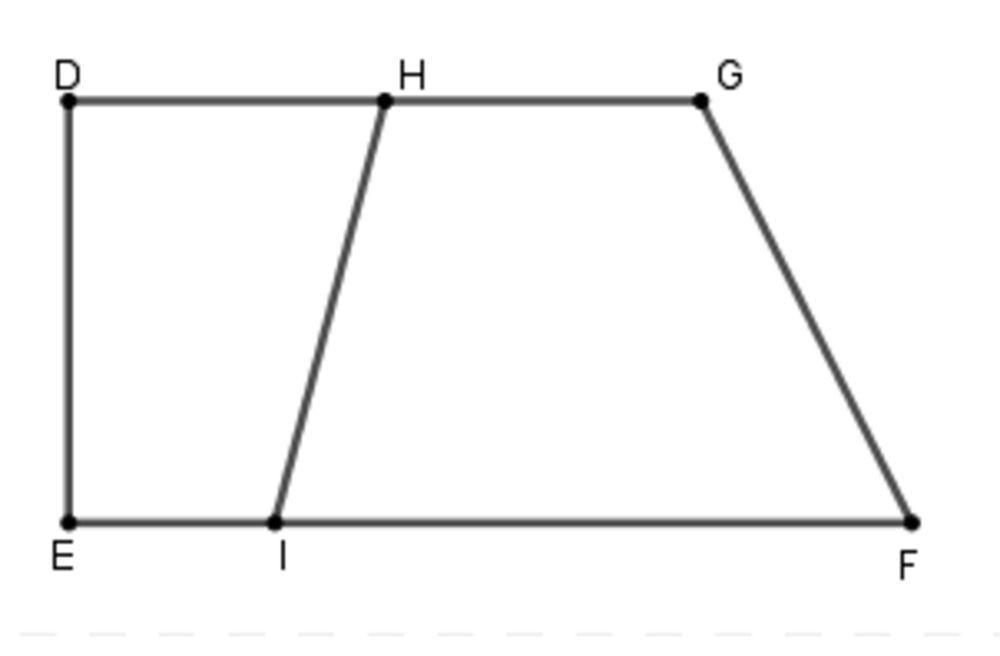
Ví dụ 2: Tìm các hình tứ giác có trong hình dưới đây:

Đáp án: Các hình tứ giác có trong hình là DEIH, HIFG, DEFG.

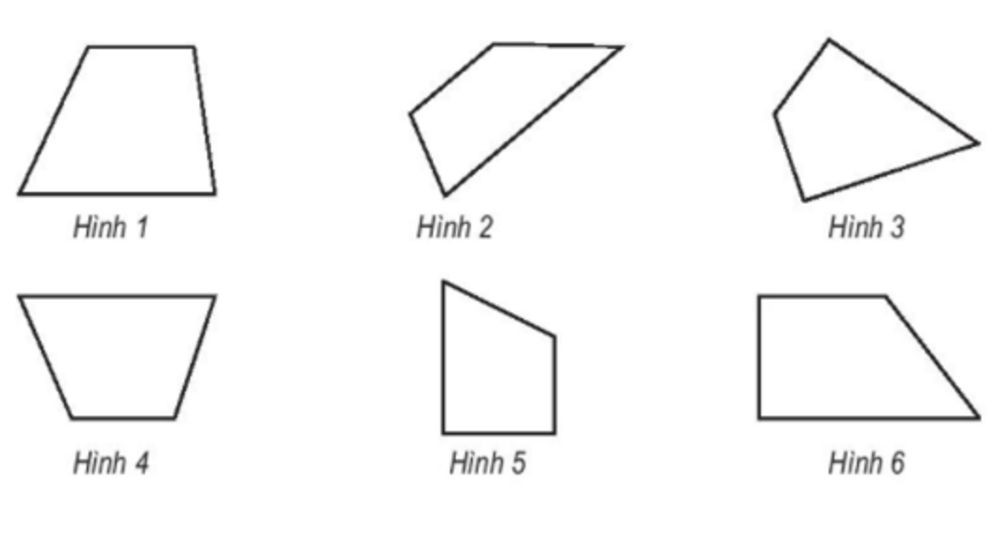
Ví dụ 3: Tìm hình thang trong các hình dưới đây?

Đáp án: Các hình thang là hình 2, hình 4, hình 5, hình 6.

6.3. Dạng 3: Tính Chu Vi, Diện Tích

Dạng bài tập này yêu cầu học sinh áp dụng các công thức để tính chu vi và diện tích của các hình tứ giác khác nhau.

Ví dụ 1: Cho hình tứ giác EFMN, biết tổng số đo các cạnh EF và FM là 52cm, tổng số đo các cạnh MN và NE là 21cm. Tính chu vi hình tứ giác EFMN.

Đáp án:

Áp dụng công thức P = a + b + c + d, ta có chu vi hình tứ giác EFMN là:

P = EF + FM + MN + NE = 52 + 21 = 73cm

Chu vi hình tứ giác EFMN là 73cm.

Ví dụ 2: Cho hình chữ nhật có chiều dài là 8cm, chu vi là 28cm. Tính chiều rộng của hình chữ nhật?

Đáp án:

Áp dụng công thức tính chu vi hình chữ nhật là P = (a + b) x 2

=> Tổng 2 cạnh là chiều dài và chiều rộng hình chữ nhật là:

a + b = P/2 = 28/2 = 14cm

=> Chiều rộng hình chữ nhật là: 14 – 8 = 6cm

Vậy chiều rộng hình chữ nhật là 6cm.

Ví dụ 3: Tính diện tích hình vuông, biết chiều dài cạnh góc vuông là 5cm.

Đáp án:

Áp dụng công thức tính diện tích hình vuông là:

S = a x a

=> Diện tích hình vuông là: 5 x 5 = 25cm²

Vậy diện tích hình vuông có cạnh 5cm là 25cm².

6.4. Dạng 4: Tính Các Góc Của Hình Tứ Giác

Dạng bài tập này yêu cầu học sinh áp dụng kiến thức về tổng các góc của hình tứ giác để tính số đo các góc còn lại.

Ví dụ: Tính tổng các góc ngoài của hình tứ giác ABCD.

Đáp án:

Vận dụng kiến thức 2 góc kề bù có tổng là 180 độ và tổng các góc trong hình tứ giác là 360 độ.

Ta có:

∠A1 + ∠B1 + ∠C1 + ∠D1 = 360°

∠B1+ ∠B2= 180°

∠C1+ ∠C2= 180°

∠D1+ ∠D2= 180°

=> ∠A1 + ∠A2 + ∠B1 + ∠B2 + ∠C1 + ∠C2 + ∠D1 + ∠D2 = 180°.4 = 720°

=> ∠A2 + ∠B2 + ∠C2 + ∠D2 = 720° – (∠A1 + ∠B1 + ∠C1 + ∠D1)

=> 720° – 360° = 360°

Vậy tổng các góc ngoài hình tứ giác ABCD là 360 độ.

7. Bí Quyết Ghi Nhớ Hiệu Quả Kiến Thức Về Hình Tứ Giác

Để giúp học sinh ghi nhớ kiến thức về hình tứ giác một cách hiệu quả, phụ huynh và giáo viên có thể áp dụng một số bí quyết sau:

7.1. Nắm Vững Kiến Thức Cơ Bản

Đảm bảo học sinh nắm vững các kiến thức cơ bản về hình tứ giác, bao gồm định nghĩa, phân loại, nhận biết các dạng hình, công thức tính diện tích và chu vi. Phụ huynh có thể kiểm tra kiến thức của con bằng cách đặt câu hỏi và yêu cầu con giải thích các khái niệm.

7.2. Học Đi Đôi Với Hành

Khuyến khích học sinh giải quyết các dạng bài tập liên quan đến hình tứ giác. Bắt đầu từ những bài tập cơ bản trong sách giáo khoa, sau đó đến các bài tập nâng cao và bài tập sưu tầm từ các nguồn khác. Việc thực hành thường xuyên sẽ giúp học sinh ghi nhớ kiến thức và áp dụng một cách hiệu quả.

7.3. Sử Dụng Phần Mềm Học Toán Sinh Động

Thay vì các hình thức học tập truyền thống, phụ huynh có thể lựa chọn cho con các phần mềm học toán sinh động, uy tín để tạo hứng thú cho trẻ. Các ứng dụng dạy toán chuẩn dựa trên chương trình đào tạo của Bộ Giáo dục và Đào tạo sẽ giúp trẻ dễ dàng nắm bắt kiến thức toán học, đặc biệt là kiến thức về hình tứ giác. Ví dụ: Monkey Math, Kyna School, Kids UP, VioEdu… Nghiên cứu từ Đại học RMIT, Khoa Công nghệ, ngày 10/05/2024 cho thấy việc sử dụng phần mềm học toán giúp tăng 30% khả năng tiếp thu kiến thức của học sinh so với phương pháp truyền thống.

8. Câu Hỏi Thường Gặp (FAQ) Về Hình Tứ Giác

1. Hình tứ giác là gì?
   Hình tứ giác là một đa giác có bốn cạnh và bốn đỉnh, trong đó không có bất kỳ hai đoạn thẳng nào cùng nằm trên một đường thẳng.

2. Có bao nhiêu loại hình tứ giác?
   Có nhiều loại hình tứ giác, bao gồm tứ giác lồi, tứ giác lõm, hình thang, hình bình hành, hình chữ nhật, hình thoi và hình vuông.

3. Làm thế nào để phân biệt hình thang và hình bình hành?
   Hình thang có ít nhất một cặp cạnh đối song song, trong khi hình bình hành có hai cặp cạnh đối song song.

4. Công thức tính diện tích hình vuông là gì?
   Diện tích hình vuông được tính bằng công thức S = a x a, trong đó a là độ dài cạnh của hình vuông.

5. Tổng các góc trong một hình tứ giác bằng bao nhiêu?
   Tổng các góc trong một hình tứ giác luôn bằng 360 độ.

6. Hình chữ nhật có phải là hình bình hành không?
   Đúng, hình chữ nhật là một trường hợp đặc biệt của hình bình hành, có bốn góc vuông.

7. Hình thoi có phải là hình vuông không?
   Không phải lúc nào hình thoi cũng là hình vuông. Hình thoi có bốn cạnh bằng nhau, nhưng chỉ khi có thêm bốn góc vuông thì nó mới trở thành hình vuông.

8. Tứ giác nội tiếp là gì?
   Tứ giác nội tiếp là hình tứ giác có bốn đỉnh nằm trên cùng một đường tròn.

9. Làm thế nào để tính chu vi của một hình tứ giác?
   Chu vi của một hình tứ giác được tính bằng cách cộng độ dài của bốn cạnh của nó: P = a + b + c + d.

10. Có những ứng dụng thực tế nào của hình tứ giác?
    Hình tứ giác được ứng dụng rộng rãi trong kiến trúc, xây dựng, thiết kế, và nhiều lĩnh vực khác. Ví dụ, các tòa nhà, cửa sổ, và nhiều vật dụng hàng ngày có hình dạng tứ giác.

Với những kiến thức và bài tập được trình bày trong bài viết này, tic.edu.vn hy vọng sẽ giúp các em học sinh ôn tập và rèn luyện kiến thức về hình tứ giác một cách hiệu quả nhất.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kiến thức và kỹ năng của mình? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả. Chúng tôi cung cấp tài liệu đa dạng, được cập nhật liên tục và kiểm duyệt kỹ càng. Hãy tham gia cộng đồng học tập trực tuyến của chúng tôi để trao đổi kiến thức và kinh nghiệm với những người cùng chí hướng.

Liên hệ với chúng tôi:

• Email: tic.edu@gmail.com
• Website: tic.edu.vn