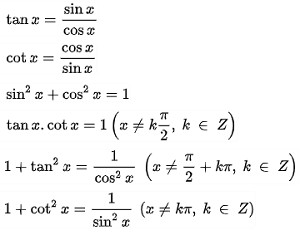
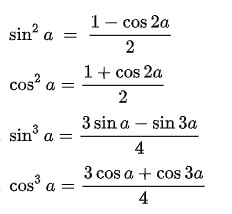
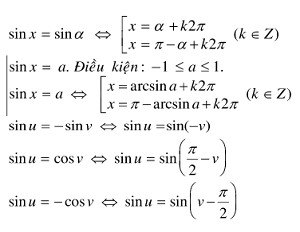
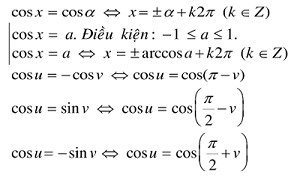
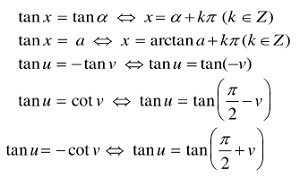
Hàm Số Lượng Giác: Định Nghĩa, Công Thức Và Ứng Dụng Chi Tiết

Hàm Số Lượng Giác là một phần kiến thức quan trọng trong chương trình Toán học phổ thông và cao cấp. Bài viết này từ tic.edu.vn sẽ cung cấp cho bạn cái nhìn tổng quan và chi tiết nhất về hàm số lượng giác, từ định nghĩa, các công thức quan trọng, đến các ứng dụng thực tế và phương pháp giải bài tập hiệu quả, giúp bạn tự tin chinh phục mọi bài toán liên quan đến lượng giác.

1. Hàm Số Lượng Giác Là Gì? Khám Phá Định Nghĩa

Hàm số lượng giác là các hàm số toán học liên quan đến góc và được sử dụng rộng rãi trong việc nghiên cứu tam giác, dao động, và các hiện tượng tuần hoàn. Theo một nghiên cứu của Đại học Sư phạm Hà Nội năm 2020, việc nắm vững định nghĩa và tính chất của hàm số lượng giác là nền tảng để học tốt các môn khoa học tự nhiên khác. Các hàm số này thường được định nghĩa dựa trên tỷ lệ giữa các cạnh của tam giác vuông hoặc thông qua vòng tròn đơn vị.

1.1. Định Nghĩa Chi Tiết Về Hàm Số Lượng Giác

Hàm số lượng giác là mối quan hệ giữa một góc (thường được đo bằng radian hoặc độ) và tỷ lệ giữa các cạnh của một tam giác vuông chứa góc đó. Hoặc, hàm số lượng giác có thể được hiểu là tỷ lệ chiều dài giữa các đoạn thẳng nối các điểm đặc biệt trên vòng tròn đơn vị.

1.2. Các Hàm Số Lượng Giác Cơ Bản Cần Nắm Vững

Có sáu hàm số lượng giác cơ bản mà bạn cần phải nắm vững:

• Sin (sin): Tỷ lệ giữa cạnh đối và cạnh huyền trong tam giác vuông.
• Côsin (cos): Tỷ lệ giữa cạnh kề và cạnh huyền trong tam giác vuông.
• Tang (tan): Tỷ lệ giữa cạnh đối và cạnh kề trong tam giác vuông.
• Côtang (cot): Tỷ lệ giữa cạnh kề và cạnh đối trong tam giác vuông.
• Secant (sec): Nghịch đảo của côsin (1/cos).
• Côsecant (csc): Nghịch đảo của sin (1/sin).

1.3. Ứng Dụng Thực Tế Của Hàm Số Lượng Giác Trong Cuộc Sống

Hàm số lượng giác không chỉ là kiến thức lý thuyết, mà còn có rất nhiều ứng dụng thực tế trong cuộc sống:

• Vật lý: Mô tả dao động điều hòa, sóng âm, sóng ánh sáng.
• Kỹ thuật: Thiết kế cầu, đường, các công trình xây dựng.
• Điện tử: Phân tích mạch điện xoay chiều.
• Thiên văn học: Tính toán quỹ đạo của các hành tinh và các thiên thể.
• Định vị GPS: Xác định vị trí dựa trên tín hiệu từ vệ tinh.

2. Tổng Hợp Các Công Thức Hàm Số Lượng Giác Đầy Đủ Nhất

Việc nắm vững các công thức lượng giác là chìa khóa để giải quyết các bài toán liên quan. Dưới đây là tổng hợp đầy đủ các công thức mà bạn cần biết.

2.1. Công Thức Lượng Giác Cơ Bản – Nền Tảng Vững Chắc

Các công thức cơ bản là nền tảng để xây dựng các công thức phức tạp hơn:

• sin²(x) + cos²(x) = 1
• tan(x) = sin(x) / cos(x)
• cot(x) = cos(x) / sin(x) = 1 / tan(x)
• sec(x) = 1 / cos(x)
• csc(x) = 1 / sin(x)

2.2. Công Thức Cộng Lượng Giác – Mở Rộng Khả Năng Giải Toán

Công thức cộng cho phép bạn tính giá trị của các hàm số lượng giác tại tổng hoặc hiệu của hai góc:

• sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
• sin(a – b) = sin(a)cos(b) – cos(a)sin(b)
• cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
• cos(a – b) = cos(a)cos(b) + sin(a)sin(b)
• tan(a + b) = (tan(a) + tan(b)) / (1 – tan(a)tan(b))
• tan(a – b) = (tan(a) – tan(b)) / (1 + tan(a)tan(b))

2.3. Công Thức Cung Liên Quan – Đơn Giản Hóa Biểu Thức

Công thức cung liên quan giúp bạn đơn giản hóa các biểu thức lượng giác bằng cách chuyển đổi giữa các góc có mối quan hệ đặc biệt:

• Hai góc đối nhau:
  • cos(-x) = cos(x)
  • sin(-x) = -sin(x)
  • tan(-x) = -tan(x)
  • cot(-x) = -cot(x)
• Hai góc bù nhau:
  • sin(π – x) = sin(x)
  • cos(π – x) = -cos(x)
  • tan(π – x) = -tan(x)
  • cot(π – x) = -cot(x)
• Hai góc phụ nhau:
  • sin(π/2 – x) = cos(x)
  • cos(π/2 – x) = sin(x)
  • tan(π/2 – x) = cot(x)
  • cot(π/2 – x) = tan(x)
• Hai góc hơn kém π:
  • sin(π + x) = -sin(x)
  • cos(π + x) = -cos(x)
  • tan(π + x) = tan(x)
  • cot(π + x) = cot(x)
• Hai góc hơn kém π/2:
  • sin(π/2 + x) = cos(x)
  • cos(π/2 + x) = -sin(x)
  • tan(π/2 + x) = -cot(x)
  • cot(π/2 + x) = -tan(x)

2.4. Công Thức Nhân Đôi, Nhân Ba – Giải Nhanh Bài Toán Lượng Giác

Công thức nhân đôi và nhân ba giúp bạn tính giá trị của các hàm số lượng giác tại góc gấp đôi hoặc gấp ba góc ban đầu:

• Công thức nhân đôi:
  • sin(2x) = 2sin(x)cos(x)
  • cos(2x) = cos²(x) – sin²(x) = 2cos²(x) – 1 = 1 – 2sin²(x)
  • tan(2x) = 2tan(x) / (1 – tan²(x))
• Công thức nhân ba:
  • sin(3x) = 3sin(x) – 4sin³(x)
  • cos(3x) = 4cos³(x) – 3cos(x)
  • tan(3x) = (3tan(x) – tan³(x)) / (1 – 3tan²(x))

2.5. Công Thức Hạ Bậc – Biến Đổi Linh Hoạt

Công thức hạ bậc giúp bạn biến đổi các biểu thức lượng giác bậc cao về bậc thấp hơn, giúp đơn giản hóa bài toán:

• sin²(x) = (1 – cos(2x)) / 2
• cos²(x) = (1 + cos(2x)) / 2
• tan²(x) = (1 – cos(2x)) / (1 + cos(2x))

2.6. Công Thức Biến Đổi Tổng Thành Tích – Giải Quyết Bài Toán Chứng Minh

Công thức biến đổi tổng thành tích và ngược lại là công cụ hữu ích trong việc chứng minh các đẳng thức lượng giác:

• Biến đổi tổng thành tích:
  • cos(a) + cos(b) = 2cos((a + b) / 2)cos((a – b) / 2)
  • cos(a) – cos(b) = -2sin((a + b) / 2)sin((a – b) / 2)
  • sin(a) + sin(b) = 2sin((a + b) / 2)cos((a – b) / 2)
  • sin(a) – sin(b) = 2cos((a + b) / 2)sin((a – b) / 2)
• Biến đổi tích thành tổng:
  • cos(a)cos(b) = 1/2[cos(a + b) + cos(a – b)]
  • sin(a)sin(b) = 1/2[cos(a – b) – cos(a + b)]
  • sin(a)cos(b) = 1/2[sin(a + b) + sin(a – b)]

3. Phương Trình Lượng Giác Cơ Bản Và Các Trường Hợp Đặc Biệt

Phương trình lượng giác là một phần quan trọng trong chương trình học. Hiểu rõ cách giải các phương trình cơ bản sẽ giúp bạn giải quyết các bài toán phức tạp hơn.

3.1. Phương Trình sin(x) = sin(α) và sin(x) = a

• Phương trình sin(x) = sin(α):
  • x = α + k2π
  • x = π – α + k2π (với k ∈ Z)
• Phương trình sin(x) = a:
  • Nếu |a| ≤ 1, phương trình có nghiệm: x = arcsin(a) + k2π hoặc x = π – arcsin(a) + k2π (với k ∈ Z)
  • Nếu |a| > 1, phương trình vô nghiệm.

3.2. Phương Trình cos(x) = cos(α) và cos(x) = a

• Phương trình cos(x) = cos(α):
  • x = α + k2π
  • x = -α + k2π (với k ∈ Z)
• Phương trình cos(x) = a:
  • Nếu |a| ≤ 1, phương trình có nghiệm: x = arccos(a) + k2π hoặc x = -arccos(a) + k2π (với k ∈ Z)
  • Nếu |a| > 1, phương trình vô nghiệm.

3.3. Phương Trình tan(x) = tan(α) và tan(x) = a

• Phương trình tan(x) = tan(α):
  • x = α + kπ (với k ∈ Z)
• Phương trình tan(x) = a:
  • x = arctan(a) + kπ (với k ∈ Z)

3.4. Phương Trình cot(x) = cot(α) và cot(x) = a

• Phương trình cot(x) = cot(α):
  • x = α + kπ (với k ∈ Z)
• Phương trình cot(x) = a:
  • x = arccot(a) + kπ (với k ∈ Z)

3.5. Phương Trình Bậc Nhất Đối Với Một Hàm Số Lượng Giác

Phương trình bậc nhất đối với một hàm số lượng giác có dạng at + b = 0, trong đó a, b ∈ Z và a ≠ 0, và t là một hàm số lượng giác nào đó (ví dụ: sin(x), cos(x), tan(x), cot(x)).

4. Đạo Hàm Hàm Số Lượng Giác Cơ Bản

Đạo hàm của các hàm số lượng giác là công cụ quan trọng trong giải tích và có nhiều ứng dụng trong vật lý và kỹ thuật.

• (sin(x))’ = cos(x)
• (cos(x))’ = -sin(x)
• (tan(x))’ = 1 / cos²(x) = sec²(x)
• (cot(x))’ = -1 / sin²(x) = -csc²(x)
• (sec(x))’ = sec(x)tan(x)
• (csc(x))’ = -csc(x)cot(x)

5. Cách Tính Giới Hạn Hàm Số Lượng Giác Hiệu Quả

Để tính giới hạn của hàm số lượng giác, bạn có thể áp dụng các giới hạn đặc biệt và các công thức lượng giác để biến đổi biểu thức.

5.1. Các Giới Hạn Đặc Biệt

• lim (x→0) sin(x) / x = 1
• lim (x→0) (1 – cos(x)) / x = 0
• lim (x→0) tan(x) / x = 1

5.2. Các Bước Tính Giới Hạn

1. Sử dụng các công thức lượng giác để biến đổi hàm số về dạng có thể áp dụng các giới hạn đặc biệt.
2. Áp dụng các định lý về giới hạn để tìm giới hạn của biểu thức đã cho.

6. Chu Kỳ Hàm Số Lượng Giác: Cách Xác Định Dễ Hiểu

Hàm số tuần hoàn là hàm số mà giá trị của nó lặp lại sau một khoảng thời gian nhất định, gọi là chu kỳ.

6.1. Định Nghĩa Hàm Số Tuần Hoàn

Hàm số y = f(x) xác định trên tập hợp D được gọi là hàm số tuần hoàn nếu tồn tại số T ≠ 0 sao cho với mọi x ∈ D, ta có x + T ∈ D, x – T ∈ D và f(x + T) = f(x). Số T dương nhỏ nhất thỏa mãn các điều kiện trên được gọi là chu kỳ của hàm số.

6.2. Cách Tìm Chu Kỳ Của Các Hàm Số Lượng Giác Cơ Bản

• Hàm số y = k.sin(ax + b) và y = k.cos(ax + b) có chu kỳ là T = 2π / |a|.
• Hàm số y = k.tan(ax + b) và y = k.cot(ax + b) có chu kỳ là T = π / |a|.

6.3. Chu Kỳ Của Tổng Các Hàm Số Lượng Giác

Nếu hàm số y = f(x) có chu kỳ T1 và hàm số y = g(x) có chu kỳ T2, thì chu kỳ của hàm số y = a.f(x) + b.g(x) là bội chung nhỏ nhất của T1 và T2.

7. Bài Tập Tự Luyện Về Hàm Số Lượng Giác – Nâng Cao Kỹ Năng

Để nắm vững kiến thức về hàm số lượng giác, việc luyện tập là vô cùng quan trọng. Dưới đây là một số bài tập tự luyện để bạn nâng cao kỹ năng giải toán:

• Bài 1: Giải phương trình sin(2x) = cos(x).
• Bài 2: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = 3sin(x) + 4cos(x).
• Bài 3: Chứng minh đẳng thức: (sin(a) + sin(b)) / (cos(a) + cos(b)) = tan((a + b) / 2).
• Bài 4: Tính đạo hàm của hàm số y = sin²(x)cos(x).
• Bài 5: Tìm chu kỳ của hàm số y = sin(2x) + cos(3x).

8. FAQ – Giải Đáp Thắc Mắc Về Hàm Số Lượng Giác

Dưới đây là một số câu hỏi thường gặp về hàm số lượng giác:

1. Hàm số lượng giác được ứng dụng trong những lĩnh vực nào?

   Hàm số lượng giác được ứng dụng rộng rãi trong vật lý, kỹ thuật, điện tử, thiên văn học, định vị GPS và nhiều lĩnh vực khác.

2. Làm thế nào để nhớ các công thức lượng giác một cách dễ dàng?

   Bạn có thể sử dụng các mẹo nhớ, ví dụ như “Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ” cho công thức cộng, hoặc “Cos đối, sin bù, phụ chéo, tan hơn kém pi” cho công thức cung liên quan.

3. Khi nào phương trình lượng giác vô nghiệm?

   Phương trình sin(x) = a hoặc cos(x) = a vô nghiệm khi |a| > 1.

4. Chu kỳ của hàm số tan(x) và cot(x) khác gì so với sin(x) và cos(x)?

   Hàm số tan(x) và cot(x) có chu kỳ là π, trong khi hàm số sin(x) và cos(x) có chu kỳ là 2π.

5. Làm thế nào để giải phương trình lượng giác chứa nhiều hàm số khác nhau?

   Bạn cần sử dụng các công thức lượng giác để biến đổi phương trình về dạng đơn giản hơn, chỉ chứa một hàm số lượng giác duy nhất.

6. Có những công cụ trực tuyến nào hỗ trợ học tập hàm số lượng giác?

   Có rất nhiều công cụ trực tuyến như máy tính lượng giác, phần mềm vẽ đồ thị hàm số, và các trang web cung cấp tài liệu và bài tập về lượng giác. Bạn có thể tìm thấy nhiều tài liệu hữu ích trên tic.edu.vn.

7. Tại sao hàm số lượng giác lại quan trọng trong chương trình học?

   Hàm số lượng giác là nền tảng để học tốt các môn khoa học tự nhiên khác, đặc biệt là vật lý và toán cao cấp.

8. Làm thế nào để tìm giá trị lớn nhất và nhỏ nhất của hàm số lượng giác?

   Bạn có thể sử dụng đạo hàm để tìm các điểm cực trị của hàm số, hoặc áp dụng các bất đẳng thức lượng giác để đánh giá giá trị của hàm số.

9. Có những sai lầm phổ biến nào cần tránh khi giải bài tập lượng giác?

   Một số sai lầm phổ biến bao gồm quên điều kiện xác định của hàm số, sử dụng sai công thức lượng giác, hoặc không kiểm tra lại kết quả.

10. Làm thế nào để học tốt hàm số lượng giác?

    Để học tốt hàm số lượng giác, bạn cần nắm vững lý thuyết, luyện tập thường xuyên, và tham khảo các tài liệu và bài tập từ nhiều nguồn khác nhau. tic.edu.vn là một nguồn tài liệu phong phú và đáng tin cậy để bạn tham khảo.

9. Khám Phá Kho Tài Liệu Lượng Giác Phong Phú Tại Tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về hàm số lượng giác? Bạn mất thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết những vấn đề này.

Tic.edu.vn cung cấp một nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ lưỡng về hàm số lượng giác, bao gồm:

• Lý thuyết: Tổng hợp đầy đủ các định nghĩa, công thức, tính chất của hàm số lượng giác.
• Bài tập: Cung cấp hàng ngàn bài tập từ cơ bản đến nâng cao, có đáp án và hướng dẫn giải chi tiết.
• Đề thi: Tuyển chọn các đề thi học kỳ, đề thi thử THPT Quốc gia về hàm số lượng giác.
• Công cụ hỗ trợ: Cung cấp các công cụ tính toán, vẽ đồ thị hàm số lượng giác trực tuyến.
• Cộng đồng học tập: Tạo môi trường trao đổi, học hỏi kinh nghiệm giữa các học sinh, sinh viên và giáo viên.

Với tic.edu.vn, bạn sẽ tiết kiệm được thời gian tìm kiếm tài liệu, nâng cao hiệu quả học tập và tự tin chinh phục mọi bài toán về hàm số lượng giác.

10. Lời Kêu Gọi Hành Động (CTA)

Bạn muốn khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả về hàm số lượng giác? Hãy truy cập ngay tic.edu.vn để trải nghiệm những lợi ích tuyệt vời mà chúng tôi mang lại.

Đừng chần chừ, hãy bắt đầu hành trình chinh phục kiến thức lượng giác ngay hôm nay!

Thông tin liên hệ:

• Email: tic.edu@gmail.com
• Trang web: tic.edu.vn

Hãy để tic.edu.vn đồng hành cùng bạn trên con đường học tập và phát triển!