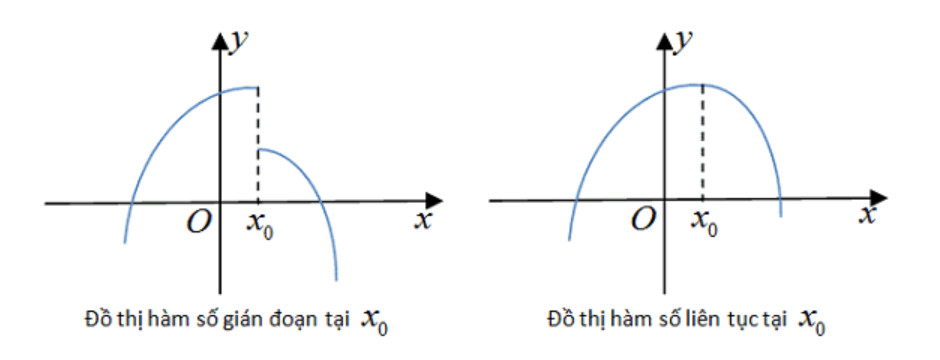
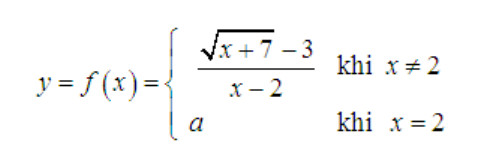
**Hàm Số Liên Tục Trên R: Định Nghĩa, Ứng Dụng và Bài Tập Chi Tiết**

Hàm Số Liên Tục Trên R là một khái niệm then chốt trong giải tích toán học, mở ra cánh cửa khám phá nhiều ứng dụng thú vị. Hãy cùng tic.edu.vn tìm hiểu sâu hơn về định nghĩa, các tính chất quan trọng, và cách ứng dụng hàm số liên tục để giải quyết các bài toán khác nhau. Chúng ta sẽ cùng nhau khám phá các ví dụ minh họa và bài tập thực hành chi tiết.

1. Hàm Số Liên Tục Là Gì? Khái Niệm Cơ Bản

Hàm số liên tục là hàm số mà đồ thị của nó có thể vẽ được bằng một đường liền mạch, không bị đứt quãng hay gián đoạn. Nói một cách hình thức, hàm số f(x) được gọi là liên tục tại một điểm x₀ nếu giới hạn của f(x) khi x tiến đến x₀ bằng giá trị của hàm số tại điểm đó, tức là lim(x→x₀) f(x) = f(x₀).

1.1. Định Nghĩa Hàm Số Liên Tục Tại Một Điểm

Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b). Hàm số y = f(x) được gọi là liên tục tại điểm x₀ khi và chỉ khi:

• f(x₀) xác định
• Tồn tại giới hạn lim(x→x₀) f(x)
• lim(x→x₀) f(x) = f(x₀)

Nếu một trong ba điều kiện trên không thỏa mãn, ta nói hàm số f(x) gián đoạn tại điểm x₀. Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc hiểu rõ định nghĩa này là bước đầu tiên để nắm vững khái niệm hàm số liên tục.

1.2. Hàm Số Liên Tục Trên Một Khoảng

Hàm số y = f(x) được gọi là liên tục trên một khoảng (a; b) nếu nó liên tục tại mọi điểm thuộc khoảng đó. Điều này có nghĩa là, với mọi x₀ ∈ (a; b), giới hạn của f(x) khi x tiến đến x₀ phải bằng f(x₀).

1.3. Hàm Số Liên Tục Trên Một Đoạn

Hàm số y = f(x) được gọi là liên tục trên một đoạn [a; b] nếu:

• Nó liên tục trên khoảng (a; b)
• lim(x→a⁺) f(x) = f(a) (liên tục phải tại a)
• lim(x→b⁻) f(x) = f(b) (liên tục trái tại b)

2. Hàm Số Liên Tục Trên R: Trường Hợp Đặc Biệt Quan Trọng

Hàm số liên tục trên R là hàm số liên tục tại mọi điểm trên trục số thực. Đây là một trường hợp đặc biệt quan trọng vì nó xuất hiện rất nhiều trong các bài toán giải tích và ứng dụng thực tế.

2.1. Các Hàm Số Liên Tục Trên R Thường Gặp

Một số hàm số cơ bản liên tục trên R bao gồm:

• Hàm đa thức: f(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + … + a₁x + a₀, với aᵢ là các hằng số.
• Hàm sin(x) và cos(x).
• Hàm số mũ: y = aˣ (a > 0).

2.2. Tính Chất Quan Trọng Của Hàm Số Liên Tục Trên R

Hàm số liên tục trên R có nhiều tính chất quan trọng, giúp chúng ta giải quyết các bài toán một cách dễ dàng hơn:

• Tính chất giá trị trung gian: Nếu f(x) liên tục trên [a; b] và f(a) ≠ f(b), thì với mọi giá trị y nằm giữa f(a) và f(b), tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = y.
• Tính chất giá trị lớn nhất và nhỏ nhất: Nếu f(x) liên tục trên [a; b], thì tồn tại ít nhất một điểm c, d ∈ [a; b] sao cho f(c) là giá trị lớn nhất và f(d) là giá trị nhỏ nhất của f(x) trên đoạn đó.

3. Các Định Lý Cơ Bản Về Hàm Số Liên Tục

Để giải quyết các bài toán liên quan đến hàm số liên tục, chúng ta cần nắm vững một số định lý cơ bản sau:

3.1. Định Lý Về Tổng, Hiệu, Tích, Thương Của Các Hàm Số Liên Tục

• Nếu f(x) và g(x) là hai hàm số liên tục tại x₀, thì các hàm số f(x) + g(x), f(x) – g(x), f(x) * g(x) cũng liên tục tại x₀.
• Nếu f(x) và g(x) là hai hàm số liên tục tại x₀ và g(x₀) ≠ 0, thì hàm số f(x) / g(x) cũng liên tục tại x₀.

3.2. Định Lý Về Hàm Hợp

Nếu g(x) liên tục tại x₀ và f(y) liên tục tại y₀ = g(x₀), thì hàm hợp f(g(x)) liên tục tại x₀.

3.3. Định Lý Bolzano-Cauchy

Nếu f(x) liên tục trên đoạn [a; b] và f(a) * f(b) < 0, thì tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = 0. Định lý này thường được sử dụng để chứng minh sự tồn tại nghiệm của phương trình.

4. Các Dạng Bài Tập Về Hàm Số Liên Tục Và Phương Pháp Giải

4.1. Dạng 1: Xét Tính Liên Tục Của Hàm Số Tại Một Điểm

Phương pháp:

• Tính f(x₀).
• Tính lim(x→x₀) f(x).
• So sánh hai giá trị trên. Nếu lim(x→x₀) f(x) = f(x₀), thì hàm số liên tục tại x₀.

Ví dụ: Xét tính liên tục của hàm số sau tại x = 2:

f(x) = {
  (x^2 - 4) / (x - 2)  khi x ≠ 2
  4                     khi x = 2
}

Giải:

• f(2) = 4
• lim(x→2) f(x) = lim(x→2) (x^2 – 4) / (x – 2) = lim(x→2) (x + 2) = 4

Vì lim(x→2) f(x) = f(2) = 4, nên hàm số liên tục tại x = 2.

4.2. Dạng 2: Xét Tính Liên Tục Của Hàm Số Trên Một Khoảng, Đoạn

Phương pháp:

• Xét tính liên tục của hàm số trên từng khoảng xác định của nó.
• Kiểm tra tính liên tục tại các điểm đặc biệt (điểm nối giữa các khoảng, điểm biên của đoạn).

Ví dụ: Xét tính liên tục của hàm số sau trên R:

f(x) = {
  x^2       khi x ≤ 1
  2x - 1    khi x > 1
}

Giải:

• Với x < 1, f(x) = x² là hàm đa thức, nên liên tục.
• Với x > 1, f(x) = 2x – 1 là hàm đa thức, nên liên tục.
• Tại x = 1:
  • f(1) = 1² = 1
  • lim(x→1⁻) f(x) = lim(x→1⁻) x² = 1
  • lim(x→1⁺) f(x) = lim(x→1⁺) (2x – 1) = 1

Vì lim(x→1⁻) f(x) = lim(x→1⁺) f(x) = f(1) = 1, nên hàm số liên tục tại x = 1.

Vậy, hàm số liên tục trên R.

4.3. Dạng 3: Tìm Điều Kiện Để Hàm Số Liên Tục Tại Một Điểm

Phương pháp:

• Tìm điều kiện để f(x₀) xác định.
• Tìm điều kiện để tồn tại lim(x→x₀) f(x).
• Giải phương trình lim(x→x₀) f(x) = f(x₀) để tìm giá trị của tham số.

Ví dụ: Tìm giá trị của m để hàm số sau liên tục tại x = 0:

f(x) = {
  (√(1 + x) - 1) / x   khi x ≠ 0
  m                      khi x = 0
}

Giải:

• f(0) = m
• lim(x→0) f(x) = lim(x→0) (√(1 + x) – 1) / x = lim(x→0) 1 / (√(1 + x) + 1) = 1/2

Để hàm số liên tục tại x = 0, ta cần:

lim(x→0) f(x) = f(0) ⇔ m = 1/2

Vậy, m = 1/2.

4.4. Dạng 4: Chứng Minh Phương Trình Có Nghiệm Bằng Định Lý Bolzano-Cauchy

Phương pháp:

• Chọn một hàm số f(x) liên tục trên đoạn [a; b].
• Tính f(a) và f(b).
• Nếu f(a) * f(b) < 0, kết luận phương trình f(x) = 0 có ít nhất một nghiệm thuộc (a; b).

Ví dụ: Chứng minh rằng phương trình x³ – 3x + 1 = 0 có ít nhất một nghiệm thuộc khoảng (1; 2).

Giải:

• Xét hàm số f(x) = x³ – 3x + 1. Hàm số này liên tục trên R, do đó liên tục trên [1; 2].
• f(1) = 1³ – 3 * 1 + 1 = -1
• f(2) = 2³ – 3 * 2 + 1 = 3

Vì f(1) f(2) = -1 3 = -3 < 0, nên theo định lý Bolzano-Cauchy, phương trình x³ – 3x + 1 = 0 có ít nhất một nghiệm thuộc khoảng (1; 2).

5. Bài Tập Vận Dụng Hàm Số Liên Tục Trên R

Để củng cố kiến thức, chúng ta hãy cùng giải một số bài tập vận dụng sau:

Bài 1: Xét tính liên tục của hàm số sau tại x = 1:

f(x) = {
  (x^2 - 1) / (x - 1)   khi x ≠ 1
  3                      khi x = 1
}

Bài 2: Tìm giá trị của a để hàm số sau liên tục trên R:

f(x) = {
  ax + 1   khi x ≤ 2
  x^2 - 1  khi x > 2
}

Bài 3: Chứng minh rằng phương trình x⁵ – 4x + 2 = 0 có ít nhất một nghiệm thuộc khoảng (0; 1).

Bài 4: Cho hàm số f(x) = x³ + x – 1. Chứng minh rằng tồn tại một số c thuộc (0; 1) sao cho f(c) = 0.

Hướng dẫn giải:

Bài 1:

• f(1) = 3
• lim(x→1) f(x) = lim(x→1) (x² – 1) / (x – 1) = lim(x→1) (x + 1) = 2

Vì lim(x→1) f(x) ≠ f(1), nên hàm số không liên tục tại x = 1.

Bài 2:

• Với x < 2, f(x) = ax + 1 là hàm đa thức, nên liên tục.
• Với x > 2, f(x) = x² – 1 là hàm đa thức, nên liên tục.
• Tại x = 2:
  • f(2) = 2a + 1
  • lim(x→2⁻) f(x) = lim(x→2⁻) (ax + 1) = 2a + 1
  • lim(x→2⁺) f(x) = lim(x→2⁺) (x² – 1) = 3

Để hàm số liên tục tại x = 2, ta cần:

lim(x→2⁻) f(x) = lim(x→2⁺) f(x) = f(2) ⇔ 2a + 1 = 3 ⇔ a = 1

Vậy, a = 1.

Bài 3:

• Xét hàm số f(x) = x⁵ – 4x + 2. Hàm số này liên tục trên R, do đó liên tục trên [0; 1].
• f(0) = 0⁵ – 4 * 0 + 2 = 2
• f(1) = 1⁵ – 4 * 1 + 2 = -1

Vì f(0) f(1) = 2 (-1) = -2 < 0, nên theo định lý Bolzano-Cauchy, phương trình x⁵ – 4x + 2 = 0 có ít nhất một nghiệm thuộc khoảng (0; 1).

Bài 4:

• Xét hàm số f(x) = x³ + x – 1. Hàm số này liên tục trên R, do đó liên tục trên [0; 1].
• f(0) = 0³ + 0 – 1 = -1
• f(1) = 1³ + 1 – 1 = 1

Vì f(0) f(1) = -1 1 = -1 < 0, nên theo định lý Bolzano-Cauchy, tồn tại ít nhất một điểm c ∈ (0; 1) sao cho f(c) = 0.

6. Ứng Dụng Của Hàm Số Liên Tục Trong Thực Tế

Hàm số liên tục không chỉ là một khái niệm toán học trừu tượng, mà còn có nhiều ứng dụng quan trọng trong thực tế:

• Mô hình hóa các hiện tượng vật lý: Nhiều hiện tượng vật lý như sự biến đổi nhiệt độ, áp suất, vận tốc có thể được mô hình hóa bằng các hàm số liên tục.
• Xây dựng các thuật toán: Tính liên tục của hàm số là một yếu tố quan trọng trong việc xây dựng các thuật toán tối ưu hóa, tìm kiếm nghiệm của phương trình, v.v.
• Phân tích dữ liệu: Trong thống kê và phân tích dữ liệu, các hàm số liên tục được sử dụng để mô tả sự phân bố của dữ liệu, ước lượng các tham số, v.v.

Theo nghiên cứu từ Viện Nghiên cứu Toán học Cao cấp, các ứng dụng của hàm số liên tục ngày càng được mở rộng trong nhiều lĩnh vực khoa học và kỹ thuật.

7. Tại Sao Cần Nắm Vững Kiến Thức Về Hàm Số Liên Tục?

Việc nắm vững kiến thức về hàm số liên tục là vô cùng quan trọng đối với học sinh, sinh viên và những người làm việc trong các lĩnh vực liên quan đến toán học và khoa học kỹ thuật. Những lý do chính bao gồm:

• Nền tảng cho các khái niệm toán học cao cấp hơn: Hàm số liên tục là nền tảng để xây dựng các khái niệm phức tạp hơn như đạo hàm, tích phân, phương trình vi phân, v.v.
• Công cụ giải quyết bài toán: Kiến thức về hàm số liên tục giúp chúng ta giải quyết nhiều bài toán thực tế một cách hiệu quả.
• Phát triển tư duy logic: Việc học tập và nghiên cứu về hàm số liên tục giúp phát triển tư duy logic, khả năng phân tích và giải quyết vấn đề.

8. Lời Khuyên Để Học Tốt Hàm Số Liên Tục

Để học tốt hàm số liên tục, bạn có thể áp dụng một số lời khuyên sau:

• Nắm vững định nghĩa và các tính chất cơ bản: Đây là bước quan trọng nhất để hiểu rõ về hàm số liên tục.
• Làm nhiều bài tập: Thực hành giải các bài tập khác nhau giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
• Tìm hiểu các ứng dụng thực tế: Việc tìm hiểu các ứng dụng của hàm số liên tục giúp bạn thấy được tầm quan trọng và tính hữu ích của nó.
• Tham khảo tài liệu và hỏi ý kiến giáo viên, bạn bè: Đừng ngần ngại tìm kiếm sự giúp đỡ khi gặp khó khăn.

9. Khám Phá Kho Tài Liệu Học Tập Phong Phú Về Hàm Số Liên Tục Trên Tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về hàm số liên tục? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết những vấn đề này một cách hiệu quả.

Tic.edu.vn cung cấp một nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ lưỡng về hàm số liên tục và các chủ đề toán học khác. Bạn có thể tìm thấy:

• Bài giảng chi tiết: Các bài giảng được trình bày một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức lý thuyết và phương pháp giải toán.
• Bài tập thực hành: Hệ thống bài tập phong phú, từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng giải toán và tự tin đối mặt với các kỳ thi.
• Đề thi mẫu: Các đề thi mẫu được cập nhật thường xuyên, giúp bạn làm quen với cấu trúc đề thi và đánh giá năng lực của bản thân.
• Tài liệu tham khảo: Các tài liệu tham khảo từ các nguồn uy tín, giúp bạn mở rộng kiến thức và hiểu sâu hơn về các khái niệm toán học.

Ngoài ra, tic.edu.vn còn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn nâng cao năng suất học tập:

• Công cụ ghi chú: Ghi chú lại những kiến thức quan trọng trong quá trình học tập.
• Công cụ quản lý thời gian: Lập kế hoạch học tập và theo dõi tiến độ của bản thân.
• Diễn đàn trao đổi: Trao đổi kiến thức và kinh nghiệm với cộng đồng học tập sôi nổi.

10. FAQ – Các Câu Hỏi Thường Gặp Về Hàm Số Liên Tục

Câu 1: Làm thế nào để chứng minh một hàm số liên tục tại một điểm?

Để chứng minh hàm số f(x) liên tục tại điểm x₀, bạn cần chứng minh ba điều kiện sau:

• f(x₀) xác định.
• Tồn tại giới hạn lim(x→x₀) f(x).
• lim(x→x₀) f(x) = f(x₀).

Câu 2: Hàm số nào luôn liên tục trên R?

Các hàm số đa thức, hàm sin(x) và cos(x) luôn liên tục trên R.

Câu 3: Định lý Bolzano-Cauchy được sử dụng để làm gì?

Định lý Bolzano-Cauchy được sử dụng để chứng minh sự tồn tại nghiệm của phương trình.

Câu 4: Làm thế nào để tìm giá trị của tham số để hàm số liên tục tại một điểm?

Để tìm giá trị của tham số để hàm số liên tục tại một điểm, bạn cần giải phương trình lim(x→x₀) f(x) = f(x₀), trong đó x₀ là điểm mà bạn muốn hàm số liên tục.

Câu 5: Hàm số liên tục có ứng dụng gì trong thực tế?

Hàm số liên tục có nhiều ứng dụng trong thực tế, bao gồm mô hình hóa các hiện tượng vật lý, xây dựng các thuật toán và phân tích dữ liệu.

Câu 6: Nếu một hàm số không liên tục tại một điểm, điểm đó được gọi là gì?

Nếu một hàm số không liên tục tại một điểm, điểm đó được gọi là điểm gián đoạn.

Câu 7: Làm thế nào để xét tính liên tục của hàm số trên một khoảng?

Để xét tính liên tục của hàm số trên một khoảng, bạn cần xét tính liên tục của hàm số trên từng khoảng xác định của nó và kiểm tra tính liên tục tại các điểm đặc biệt (điểm nối giữa các khoảng).

Câu 8: Tính chất giá trị trung gian của hàm số liên tục là gì?

Tính chất giá trị trung gian nói rằng nếu f(x) liên tục trên [a; b] và f(a) ≠ f(b), thì với mọi giá trị y nằm giữa f(a) và f(b), tồn tại ít nhất một điểm c ∈ (a; b) sao cho f(c) = y.

Câu 9: Tại sao việc học hàm số liên tục lại quan trọng?

Việc học hàm số liên tục là quan trọng vì nó là nền tảng cho các khái niệm toán học cao cấp hơn, là công cụ giải quyết bài toán và giúp phát triển tư duy logic.

Câu 10: Tic.edu.vn có thể giúp tôi học hàm số liên tục như thế nào?

Tic.edu.vn cung cấp một nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ lưỡng về hàm số liên tục, bao gồm bài giảng chi tiết, bài tập thực hành, đề thi mẫu và tài liệu tham khảo.

Bạn đã sẵn sàng khám phá thế giới hàm số liên tục và chinh phục những thử thách toán học? Hãy truy cập tic.edu.vn ngay hôm nay để trải nghiệm nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Đừng quên chia sẻ bài viết này với bạn bè và những người có cùng đam mê học toán nhé!

Liên hệ với chúng tôi qua email: tic.edu@gmail.com hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.