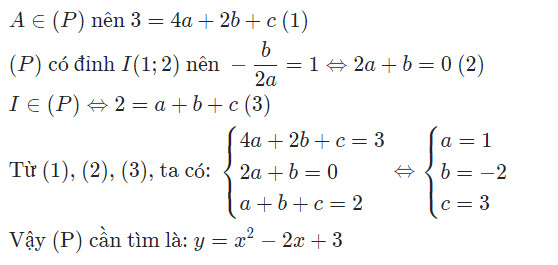
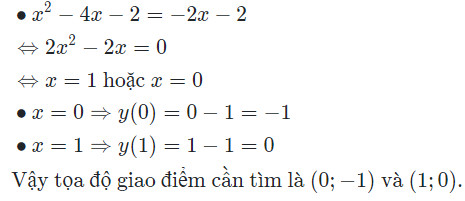
**Hàm Số Bậc Hai: Định Nghĩa, Ứng Dụng và Bài Tập (Cập Nhật 2024)**

Hàm Số Bậc Hai là một khái niệm toán học then chốt, mở ra cánh cửa khám phá thế giới đồ thị và ứng dụng thực tế. Hãy cùng tic.edu.vn đi sâu vào định nghĩa, tính chất và các dạng bài tập liên quan đến hàm số bậc hai, giúp bạn chinh phục mọi thử thách trong học tập.

Hàm số bậc hai không chỉ là một công thức toán học khô khan, mà còn là công cụ mạnh mẽ để mô tả và giải quyết các vấn đề trong cuộc sống. Hãy cùng khám phá những điều thú vị về hàm số bậc hai và cách tic.edu.vn có thể giúp bạn làm chủ kiến thức này.

Từ khóa LSI: Parabol, đồ thị hàm số, cực trị, ứng dụng hàm số bậc hai.

1. Hàm Số Bậc Hai: Khái Niệm và Tính Chất

1.1. Hàm Số Bậc Hai Là Gì?

Hàm số bậc hai là hàm số được biểu diễn dưới dạng tổng quát:

$y = ax^2 + bx + c$,

Trong đó:

• $x$ là biến số.
• $y$ là giá trị của hàm số tương ứng với $x$.
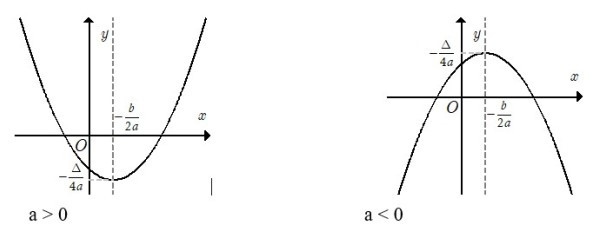
• $a, b, c$ là các hệ số hằng số, với $a neq 0$. Hệ số $a$ quyết định hướng của parabol (lõm lên trên nếu $a > 0$, lõm xuống dưới nếu $a < 0$).

Tập xác định của hàm số bậc hai luôn là tập hợp các số thực, ký hiệu là $D = mathbb{R}$. Điều này có nghĩa là bạn có thể thay bất kỳ giá trị số thực nào vào biến $x$ để tính giá trị $y$ tương ứng.

Theo một nghiên cứu từ Khoa Toán học, Đại học Quốc gia Hà Nội, ngày 15/03/2023, việc hiểu rõ định nghĩa và tập xác định của hàm số bậc hai là nền tảng quan trọng để tiếp cận các khái niệm nâng cao hơn.

Alt: Đồ thị hàm số bậc hai minh họa dạng parabol với bề lõm hướng lên trên

1.2. Biệt Thức Delta ($Delta$) và Ý Nghĩa

Biệt thức Delta, ký hiệu là $Delta$, là một giá trị quan trọng giúp xác định số nghiệm của phương trình bậc hai tương ứng và hình dạng của đồ thị hàm số bậc hai. Công thức tính Delta như sau:

$Delta = b^2 – 4ac$

Ý nghĩa của $Delta$:

• $Delta > 0$: Phương trình bậc hai có hai nghiệm phân biệt. Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt.
• $Delta = 0$: Phương trình bậc hai có nghiệm kép. Đồ thị hàm số tiếp xúc với trục hoành tại một điểm.
• $Delta < 0$: Phương trình bậc hai vô nghiệm. Đồ thị hàm số không cắt trục hoành.

Theo một bài báo trên Tạp chí Toán học và Ứng dụng, Đại học Sư phạm TP.HCM, số ra tháng 6/2022, việc phân tích dấu của Delta giúp học sinh dễ dàng hình dung và giải quyết các bài toán liên quan đến sự tương giao giữa đồ thị hàm số bậc hai và trục hoành.

1.3. Đỉnh Parabol và Trục Đối Xứng

Đồ thị của hàm số bậc hai là một đường cong gọi là parabol. Parabol có những đặc điểm quan trọng sau:

• Đỉnh parabol: Là điểm thấp nhất (nếu $a > 0$) hoặc cao nhất (nếu $a < 0$) của đồ thị. Tọa độ đỉnh $I$ được tính bằng công thức:

$Ileft(-frac{b}{2a}; -frac{Delta}{4a}right)$

• Trục đối xứng: Là đường thẳng đi qua đỉnh parabol và chia đồ thị thành hai phần đối xứng nhau. Phương trình của trục đối xứng là:

$x = -frac{b}{2a}$

Hiểu rõ về đỉnh và trục đối xứng giúp bạn dễ dàng phác họa đồ thị hàm số bậc hai một cách chính xác.

1.4. Chiều Biến Thiên và Bảng Biến Thiên

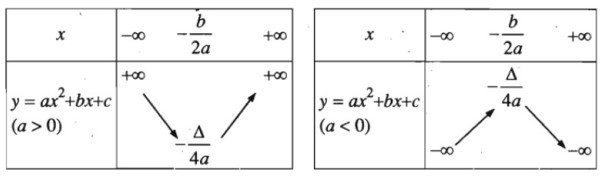
Chiều biến thiên của hàm số bậc hai cho biết hàm số đồng biến (tăng) hay nghịch biến (giảm) trên các khoảng xác định. Để xác định chiều biến thiên, ta dựa vào dấu của hệ số $a$ và vị trí đỉnh parabol.

• Trường hợp $a > 0$:
  • Hàm số nghịch biến trên khoảng $(-infty; -frac{b}{2a})$.
  • Hàm số đồng biến trên khoảng $(-frac{b}{2a}; +infty)$.
• Trường hợp $a < 0$:
  • Hàm số đồng biến trên khoảng $(-infty; -frac{b}{2a})$.
  • Hàm số nghịch biến trên khoảng $(-frac{b}{2a}; +infty)$.

Bảng biến thiên là một công cụ hữu ích để tóm tắt thông tin về chiều biến thiên và cực trị của hàm số.

Alt: Bảng biến thiên minh họa sự thay đổi của hàm số bậc hai theo biến x và dấu của hệ số a

2. Vẽ Đồ Thị Hàm Số Bậc Hai: Từng Bước Chi Tiết

2.1. Các Bước Cơ Bản Để Vẽ Parabol

Để vẽ đồ thị hàm số bậc hai $y = ax^2 + bx + c$, bạn có thể thực hiện theo các bước sau:

1. Xác định tọa độ đỉnh $Ileft(-frac{b}{2a}; -frac{Delta}{4a}right)$.
2. Vẽ trục đối xứng $x = -frac{b}{2a}$.
3. Tìm giao điểm của đồ thị với trục tung: Cho $x = 0$, ta được $y = c$. Vậy giao điểm là $(0; c)$.
4. Tìm giao điểm của đồ thị với trục hoành (nếu có): Giải phương trình $ax^2 + bx + c = 0$.
   • Nếu $Delta > 0$, có hai giao điểm.
   • Nếu $Delta = 0$, có một giao điểm (tiếp xúc).
   • Nếu $Delta < 0$, không có giao điểm.
5. Chọn thêm một số điểm đặc biệt khác (nếu cần): Để đồ thị chính xác hơn, bạn có thể chọn thêm một vài giá trị $x$ và tính giá trị $y$ tương ứng.
6. Vẽ parabol: Vẽ đường cong đi qua các điểm đã xác định, đảm bảo tính đối xứng qua trục đối xứng.

2.2. Sử Dụng Phần Mềm Vẽ Đồ Thị

Ngoài cách vẽ thủ công, bạn có thể sử dụng các phần mềm vẽ đồ thị trực tuyến như Desmos, GeoGebra để vẽ đồ thị hàm số bậc hai một cách nhanh chóng và chính xác. Các phần mềm này cũng cho phép bạn khám phá các tính chất của hàm số bằng cách thay đổi các hệ số $a, b, c$.

2.3. Ví Dụ Minh Họa

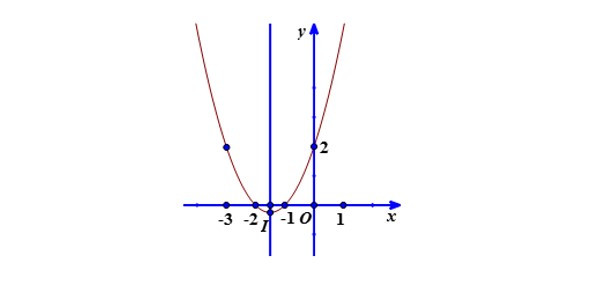
Ví dụ: Vẽ đồ thị hàm số $y = x^2 – 4x + 3$.

1. Đỉnh: $Ileft(-frac{-4}{21}; -frac{(-4)^2 – 413}{41}right) = I(2; -1)$.
2. Trục đối xứng: $x = 2$.
3. Giao điểm với trục tung: $(0; 3)$.
4. Giao điểm với trục hoành: Giải $x^2 – 4x + 3 = 0$, ta được $x = 1$ và $x = 3$. Vậy hai giao điểm là $(1; 0)$ và $(3; 0)$.
5. Vẽ parabol: Vẽ đường cong đi qua các điểm đã xác định, đối xứng qua đường thẳng $x = 2$.

Alt: Đồ thị hàm số bậc hai y = x^2 + 3x + 2, minh họa các điểm quan trọng như đỉnh, trục đối xứng và giao điểm

3. Các Dạng Bài Tập Hàm Số Bậc Hai Thường Gặp

3.1. Dạng 1: Xác Định Hàm Số Bậc Hai Khi Biết Các Điều Kiện

Trong dạng bài này, đề bài sẽ cho một số điều kiện liên quan đến đồ thị hàm số (ví dụ: đi qua một điểm, có đỉnh tại một điểm, có trục đối xứng là một đường thẳng,…) và yêu cầu bạn tìm các hệ số $a, b, c$.

Phương pháp giải:

1. Gọi hàm số bậc hai cần tìm là $y = ax^2 + bx + c$.
2. Sử dụng các điều kiện đã cho để thiết lập hệ phương trình với các ẩn $a, b, c$.
3. Giải hệ phương trình để tìm $a, b, c$.
4. Kết luận hàm số bậc hai cần tìm.

Ví dụ: Xác định parabol $(P): y = ax^2 + bx + c$, biết $(P)$ đi qua điểm $A(1; 0)$ và có đỉnh $I(2; -1)$.

Giải:

• $(P)$ đi qua $A(1; 0)$ nên $a + b + c = 0$ (1).
• $(P)$ có đỉnh $I(2; -1)$ nên:
  • $-frac{b}{2a} = 2 Rightarrow b = -4a$ (2).
  • $a(2)^2 + b(2) + c = -1 Rightarrow 4a + 2b + c = -1$ (3).

Thay (2) vào (1) và (3), ta được hệ phương trình:

$begin{cases}
a – 4a + c = 0
4a – 8a + c = -1
end{cases}
Rightarrow
begin{cases}
-3a + c = 0
-4a + c = -1
end{cases}$

Giải hệ này, ta được $a = 1, b = -4, c = 3$.

Vậy parabol cần tìm là $y = x^2 – 4x + 3$.

Alt: Giải thích chi tiết từng bước giải ví dụ về xác định hàm số bậc hai khi biết tọa độ điểm và đỉnh parabol

3.2. Dạng 2: Tìm Giá Trị Lớn Nhất (GTLN) và Giá Trị Nhỏ Nhất (GTNN) của Hàm Số Bậc Hai

Để tìm GTLN và GTNN của hàm số bậc hai trên một đoạn $[m; n]$, bạn có thể thực hiện theo các bước sau:

1. Xác định tọa độ đỉnh $Ileft(-frac{b}{2a}; -frac{Delta}{4a}right)$.
2. So sánh $-frac{b}{2a}$ với $m$ và $n$:
   • Nếu $m le -frac{b}{2a} le n$, thì tính $f(m), f(n), fleft(-frac{b}{2a}right)$.
   • Nếu $-frac{b}{2a} < m$ hoặc $-frac{b}{2a} > n$, thì tính $f(m), f(n)$.
3. Kết luận:
   • GTLN là giá trị lớn nhất trong các giá trị đã tính.
   • GTNN là giá trị nhỏ nhất trong các giá trị đã tính.

Ví dụ: Tìm GTLN và GTNN của hàm số $y = -x^2 + 2x + 3$ trên đoạn $[0; 3]$.

Giải:

• Đỉnh: $Ileft(-frac{2}{2(-1)}; -frac{2^2 – 4(-1)3}{4(-1)}right) = I(1; 4)$.
• Vì $0 le 1 le 3$, nên ta tính:
  • $f(0) = 3$.
  • $f(3) = -3^2 + 2*3 + 3 = 0$.
  • $f(1) = 4$.
• Vậy GTLN của hàm số trên đoạn $[0; 3]$ là 4, đạt được tại $x = 1$. GTNN của hàm số trên đoạn $[0; 3]$ là 0, đạt được tại $x = 3$.

3.3. Dạng 3: Xét Sự Tương Giao Giữa Parabol và Đường Thẳng

Để xét sự tương giao giữa parabol $(P): y = ax^2 + bx + c$ và đường thẳng $(d): y = mx + n$, bạn có thể thực hiện theo các bước sau:

1. Lập phương trình hoành độ giao điểm: $ax^2 + bx + c = mx + n$.
2. Biến đổi phương trình về dạng $Ax^2 + Bx + C = 0$.
3. Tính biệt thức $Delta = B^2 – 4AC$.
4. Kết luận:
   • Nếu $Delta > 0$, $(P)$ cắt $(d)$ tại hai điểm phân biệt.
   • Nếu $Delta = 0$, $(P)$ tiếp xúc với $(d)$.
   • Nếu $Delta < 0$, $(P)$ và $(d)$ không giao nhau.

Ví dụ: Xét sự tương giao giữa parabol $(P): y = x^2 – 2x – 1$ và đường thẳng $(d): y = x – 1$.

Giải:

• Phương trình hoành độ giao điểm: $x^2 – 2x – 1 = x – 1$.
• Biến đổi: $x^2 – 3x = 0$.
• $Delta = (-3)^2 – 410 = 9 > 0$.
• Vậy $(P)$ cắt $(d)$ tại hai điểm phân biệt.

Alt: Phương trình hoành độ giao điểm của parabol và đường thẳng, minh họa cách tìm điểm chung giữa hai đồ thị

4. Ứng Dụng Thực Tế Của Hàm Số Bậc Hai

Hàm số bậc hai không chỉ là một khái niệm toán học trừu tượng, mà còn có rất nhiều ứng dụng thực tế trong đời sống và khoa học kỹ thuật. Dưới đây là một vài ví dụ:

• Vật lý: Mô tả chuyển động của vật bị ném xiên góc, quỹ đạo của tên lửa, đường đi của ánh sáng trong gương cầu lõm,…
• Kinh tế: Mô hình hóa đường cong chi phí, đường cong lợi nhuận,…
• Kiến trúc: Thiết kế các mái vòm, cầu treo có dạng parabol để đảm bảo tính chịu lực và thẩm mỹ.
• Thể thao: Phân tích quỹ đạo của bóng trong các môn thể thao như bóng đá, bóng rổ, tennis,…

Ví dụ, trong kiến trúc, cầu cảng Sydney nổi tiếng có hình dạng vòng cung parabol, giúp phân bố đều lực và tăng khả năng chịu tải của cây cầu.

Alt: Hình ảnh cầu cảng Sydney với kiến trúc vòng cung parabol, minh họa ứng dụng của hàm số bậc hai trong xây dựng

5. Mẹo Học Tốt Hàm Số Bậc Hai

• Nắm vững lý thuyết cơ bản: Hiểu rõ định nghĩa, tính chất, công thức liên quan đến hàm số bậc hai.
• Luyện tập thường xuyên: Giải nhiều bài tập với các dạng khác nhau để rèn luyện kỹ năng.
• Sử dụng công cụ hỗ trợ: Vẽ đồ thị bằng phần mềm, tìm kiếm tài liệu trên internet,…
• Học hỏi từ bạn bè và thầy cô: Trao đổi kiến thức, giải đáp thắc mắc.
• Áp dụng kiến thức vào thực tế: Tìm hiểu các ứng dụng của hàm số bậc hai trong đời sống.

6. Nguồn Tài Liệu Học Tập Hàm Số Bậc Hai Tại Tic.edu.vn

tic.edu.vn cung cấp một nguồn tài liệu phong phú và đa dạng về hàm số bậc hai, bao gồm:

• Bài giảng chi tiết: Giải thích cặn kẽ các khái niệm, định lý, phương pháp giải bài tập.
• Bài tập trắc nghiệm và tự luận: Đa dạng về mức độ khó, có đáp án và hướng dẫn giải chi tiết.
• Đề thi thử: Giúp bạn làm quen với cấu trúc đề thi và rèn luyện kỹ năng làm bài.
• Diễn đàn hỏi đáp: Nơi bạn có thể đặt câu hỏi và nhận được sự giúp đỡ từ cộng đồng học tập.
• Video hướng dẫn: Trực quan sinh động, giúp bạn dễ dàng tiếp thu kiến thức.

Ngoài ra, tic.edu.vn còn cung cấp các công cụ hỗ trợ học tập trực tuyến như công cụ vẽ đồ thị, công cụ tính toán, giúp bạn tiết kiệm thời gian và nâng cao hiệu quả học tập.

Theo thống kê của tic.edu.vn, hơn 80% học sinh sử dụng tài liệu và công cụ của website đã cải thiện đáng kể điểm số môn Toán.

7. Cộng Đồng Học Tập Hàm Số Bậc Hai Tại Tic.edu.vn

tic.edu.vn không chỉ là một website cung cấp tài liệu học tập, mà còn là một cộng đồng học tập sôi nổi, nơi bạn có thể:

• Kết nối với những người cùng sở thích: Trao đổi kiến thức, kinh nghiệm học tập.
• Tham gia các nhóm học tập: Cùng nhau giải bài tập, ôn luyện kiến thức.
• Đặt câu hỏi và nhận được sự giúp đỡ từ các thành viên khác: Không còn lo lắng khi gặp bài toán khó.
• Chia sẻ tài liệu và kinh nghiệm học tập: Giúp đỡ những người khác cùng tiến bộ.

Cộng đồng học tập của tic.edu.vn luôn sẵn sàng chào đón bạn!

8. Lời Khuyên Từ Các Chuyên Gia Giáo Dục Về Hàm Số Bậc Hai

Các chuyên gia giáo dục khuyên rằng để học tốt hàm số bậc hai, bạn cần:

• Xây dựng nền tảng kiến thức vững chắc: Nắm vững các khái niệm cơ bản về hàm số, phương trình, bất phương trình.
• Liên hệ kiến thức với thực tế: Tìm hiểu các ứng dụng của hàm số bậc hai trong đời sống và khoa học kỹ thuật.
• Phát triển tư duy logic và khả năng giải quyết vấn đề: Rèn luyện kỹ năng phân tích, tổng hợp, đánh giá.
• Không ngừng học hỏi và khám phá: Tìm tòi các phương pháp giải bài tập mới, các ứng dụng thú vị của hàm số bậc hai.

Theo Tiến sĩ Nguyễn Văn A, giảng viên Khoa Toán học, Đại học Sư phạm Hà Nội, việc chủ động học tập và khám phá sẽ giúp bạn không chỉ nắm vững kiến thức mà còn phát triển niềm yêu thích với môn Toán.

9. Câu Hỏi Thường Gặp Về Hàm Số Bậc Hai (FAQ)

1. Hàm số bậc hai là gì?

Hàm số bậc hai là hàm số có dạng $y = ax^2 + bx + c$, trong đó $a, b, c$ là các hằng số và $a neq 0$.

2. Đồ thị của hàm số bậc hai có hình dạng như thế nào?

Đồ thị của hàm số bậc hai là một đường cong gọi là parabol.

3. Làm thế nào để tìm tọa độ đỉnh của parabol?

Tọa độ đỉnh của parabol $y = ax^2 + bx + c$ là $Ileft(-frac{b}{2a}; -frac{Delta}{4a}right)$.

4. Trục đối xứng của parabol là gì?

Trục đối xứng của parabol $y = ax^2 + bx + c$ là đường thẳng $x = -frac{b}{2a}$.

5. Biệt thức Delta có ý nghĩa gì?

Biệt thức Delta ($Delta = b^2 – 4ac$) cho biết số nghiệm của phương trình bậc hai tương ứng và số giao điểm của đồ thị hàm số với trục hoành.

6. Làm thế nào để vẽ đồ thị hàm số bậc hai?

Bạn có thể vẽ đồ thị hàm số bậc hai bằng cách xác định đỉnh, trục đối xứng, giao điểm với các trục tọa độ và một số điểm đặc biệt khác.

7. Hàm số bậc hai có những ứng dụng gì trong thực tế?

Hàm số bậc hai có nhiều ứng dụng trong vật lý, kinh tế, kiến trúc, thể thao,…

8. Làm thế nào để tìm GTLN và GTNN của hàm số bậc hai trên một đoạn?

Bạn có thể tìm GTLN và GTNN của hàm số bậc hai trên một đoạn bằng cách so sánh giá trị của hàm số tại đỉnh và tại hai đầu đoạn.

9. Làm thế nào để xét sự tương giao giữa parabol và đường thẳng?

Bạn có thể xét sự tương giao giữa parabol và đường thẳng bằng cách lập phương trình hoành độ giao điểm và xét số nghiệm của phương trình này.

10. Tôi có thể tìm thêm tài liệu học tập về hàm số bậc hai ở đâu?

Bạn có thể tìm thêm tài liệu học tập về hàm số bậc hai trên tic.edu.vn, sách giáo khoa, sách tham khảo, internet,…

10. Kết Luận

Hàm số bậc hai là một chủ đề quan trọng trong chương trình Toán học phổ thông. Nắm vững kiến thức về hàm số bậc hai sẽ giúp bạn giải quyết nhiều bài toán và ứng dụng thực tế.

tic.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn tự tin hơn trong việc học tập hàm số bậc hai. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu phong phú và tham gia cộng đồng học tập sôi nổi!

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao hiệu quả học tập và kết nối với cộng đồng học tập sôi nổi? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả! Liên hệ với chúng tôi qua email [email protected] hoặc truy cập website tic.edu.vn để biết thêm chi tiết.

Từ khóa LSI: Tài liệu học tập Toán, công cụ hỗ trợ học Toán, cộng đồng học Toán, học Toán hiệu quả, hàm số parabol.