Giao Điểm Là Gì? Khám Phá Định Nghĩa, Ứng Dụng Và Bài Tập Hay

Giao điểm là gì? Đây là câu hỏi mà nhiều bạn học sinh, sinh viên thường gặp phải. Bài viết này từ tic.edu.vn sẽ cung cấp cho bạn định nghĩa chi tiết về giao điểm, cách xác định giao điểm của hai đường thẳng, cùng các dạng bài tập thú vị và ứng dụng thực tế của nó, giúp bạn nắm vững kiến thức và tự tin chinh phục các bài toán liên quan.

1. Giao Điểm Là Gì? Định Nghĩa Và Khái Niệm Cơ Bản

Giao điểm là điểm chung duy nhất của hai hay nhiều đường thẳng cắt nhau. Khi hai đường thẳng cắt nhau, chúng có duy nhất một điểm chung, và điểm này chính là giao điểm của chúng. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc nắm vững khái niệm giao điểm là nền tảng để hiểu sâu hơn về hình học phẳng và giải quyết các bài toán liên quan.

• Định nghĩa: Điểm chung duy nhất của hai đường thẳng cắt nhau được gọi là giao điểm.
• Khái niệm mở rộng: Giao điểm không chỉ giới hạn ở đường thẳng, mà còn có thể áp dụng cho các hình học khác như đường tròn, mặt phẳng, v.v.

1.1. Cách Xác Định Giao Điểm Của Hai Đường Thẳng

Để xác định giao điểm của hai đường thẳng, ta cần tìm một điểm thỏa mãn đồng thời phương trình của cả hai đường thẳng đó.

• Phương pháp đại số: Giải hệ phương trình gồm hai phương trình đường thẳng để tìm tọa độ giao điểm.
• Phương pháp hình học: Vẽ hai đường thẳng trên cùng một hệ trục tọa độ và xác định điểm cắt nhau bằng mắt thường (phương pháp này thường được sử dụng để kiểm tra kết quả).

1.2. Điều Kiện Để Hai Đường Thẳng Cắt Nhau

Hai đường thẳng cắt nhau khi và chỉ khi chúng không song song và không trùng nhau.

• Trong mặt phẳng: Hai đường thẳng có hệ số góc khác nhau sẽ cắt nhau.
• Trong không gian: Hai đường thẳng không song song và không đồng phẳng sẽ cắt nhau.

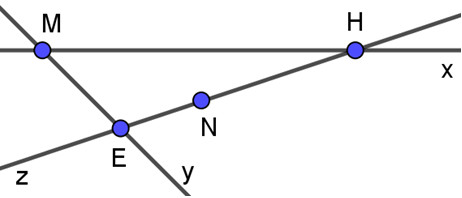
Hình ảnh minh họa giao điểm của các đường thẳng x, y, z tại các điểm M, H, E. Nắm vững kiến thức cơ bản về giao điểm giúp học sinh tự tin giải quyết các bài tập hình học.

2. Các Dạng Toán Thường Gặp Về Giao Điểm Và Phương Pháp Giải

Giao điểm là một khái niệm quan trọng trong hình học và thường xuất hiện trong nhiều bài toán khác nhau. Dưới đây là một số dạng toán thường gặp và phương pháp giải chi tiết, giúp bạn tự tin chinh phục mọi thử thách.

2.1. Dạng 1: Tìm Tọa Độ Giao Điểm Của Hai Đường Thẳng

Đây là dạng toán cơ bản nhất, yêu cầu bạn tìm tọa độ của điểm chung giữa hai đường thẳng.

• Phương pháp giải:
  1. Lập hệ phương trình: Viết phương trình của hai đường thẳng dưới dạng tổng quát (ví dụ: y = ax + b).
  2. Giải hệ phương trình: Sử dụng phương pháp thế hoặc phương pháp cộng đại số để tìm ra giá trị của x và y.
  3. Kết luận: Tọa độ (x, y) chính là tọa độ giao điểm của hai đường thẳng.

Ví dụ: Tìm giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4.

Giải:

• Lập hệ phương trình:
  • y = 2x + 1
  • y = -x + 4
• Giải hệ phương trình:
  • 2x + 1 = -x + 4
  • 3x = 3
  • x = 1
  • y = 2(1) + 1 = 3
• Kết luận: Giao điểm của hai đường thẳng là (1, 3).

2.2. Dạng 2: Xác Định Số Giao Điểm Của Nhiều Đường Thẳng

Dạng toán này yêu cầu bạn tính số giao điểm tối đa có thể tạo ra từ một số lượng đường thẳng nhất định, với điều kiện không có ba đường thẳng nào đồng quy (cùng đi qua một điểm).

• Phương pháp giải:
  1. Công thức: Số giao điểm tối đa của n đường thẳng là n(n-1)/2.
  2. Giải thích: Mỗi đường thẳng sẽ cắt n-1 đường thẳng còn lại. Tuy nhiên, mỗi giao điểm được tính hai lần (ví dụ: giao điểm của đường thẳng A và B cũng là giao điểm của đường thẳng B và A), vì vậy cần chia cho 2.

Ví dụ: Cho 5 đường thẳng, hỏi có tối đa bao nhiêu giao điểm?

Giải:

• Áp dụng công thức: 5(5-1)/2 = 10
• Kết luận: Có tối đa 10 giao điểm.

2.3. Dạng 3: Chứng Minh Ba Đường Thẳng Đồng Quy

Dạng toán này yêu cầu bạn chứng minh ba đường thẳng cùng đi qua một điểm.

• Phương pháp giải:
  1. Tìm giao điểm của hai đường thẳng: Chọn hai đường thẳng bất kỳ và tìm giao điểm của chúng (gọi là điểm A).
  2. Kiểm tra điểm A có thuộc đường thẳng còn lại không: Thay tọa độ điểm A vào phương trình của đường thẳng thứ ba. Nếu phương trình được thỏa mãn, thì ba đường thẳng đồng quy tại điểm A.

Ví dụ: Chứng minh ba đường thẳng sau đồng quy:

• d1: y = x + 1
• d2: y = -x + 3
• d3: y = 2x

Giải:

• Tìm giao điểm của d1 và d2:
  • x + 1 = -x + 3
  • 2x = 2
  • x = 1
  • y = 1 + 1 = 2
  • Giao điểm A(1, 2)
• Kiểm tra điểm A có thuộc d3 không:
  • 2 = 2(1) (thỏa mãn)
• Kết luận: Ba đường thẳng d1, d2, d3 đồng quy tại điểm A(1, 2).

2.4. Dạng 4: Tìm Điều Kiện Để Ba Đường Thẳng Đồng Quy

Dạng toán này phức tạp hơn, yêu cầu bạn tìm một điều kiện (thường là một tham số) để ba đường thẳng đồng quy.

• Phương pháp giải:
  1. Tìm giao điểm của hai đường thẳng: Chọn hai đường thẳng bất kỳ (thường là hai đường thẳng có phương trình đơn giản nhất) và tìm giao điểm của chúng (gọi là điểm A).
  2. Thay tọa độ điểm A vào phương trình đường thẳng còn lại: Thay tọa độ điểm A vào phương trình của đường thẳng thứ ba. Bạn sẽ thu được một phương trình chứa tham số cần tìm.
  3. Giải phương trình: Giải phương trình để tìm giá trị của tham số.

Ví dụ: Tìm giá trị của m để ba đường thẳng sau đồng quy:

• d1: y = x + 1
• d2: y = -x + 3
• d3: y = mx + 2

Giải:

• Tìm giao điểm của d1 và d2: (tương tự như ví dụ trên) Giao điểm A(1, 2)
• Thay tọa độ điểm A vào phương trình d3:
  • 2 = m(1) + 2
  • m = 0
• Kết luận: Ba đường thẳng d1, d2, d3 đồng quy khi m = 0.

2.5. Dạng 5: Ứng Dụng Giao Điểm Trong Các Bài Toán Thực Tế

Giao điểm không chỉ là một khái niệm trừu tượng trong hình học, mà còn có nhiều ứng dụng trong thực tế, ví dụ như trong các bài toán về định vị, thiết kế kỹ thuật, v.v.

Ví dụ: Hai tàu biển di chuyển trên hai đường thẳng khác nhau. Làm thế nào để xác định vị trí có thể xảy ra va chạm giữa hai tàu?

Giải: Vị trí có thể xảy ra va chạm chính là giao điểm của hai đường thẳng mà hai tàu đang di chuyển. Bằng cách tìm tọa độ giao điểm, ta có thể xác định được vị trí nguy hiểm và đưa ra cảnh báo kịp thời.

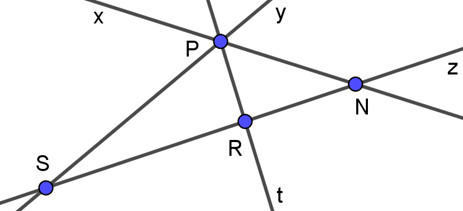
Hình ảnh minh họa các giao điểm của nhiều đường thẳng. Việc luyện tập các dạng bài tập khác nhau giúp học sinh nắm vững kiến thức và phát triển tư duy giải toán.

3. Bài Tập Vận Dụng Về Giao Điểm Của Hai Đường Thẳng

Để củng cố kiến thức và rèn luyện kỹ năng giải toán, hãy cùng thử sức với một số bài tập vận dụng sau đây.

Bài 1. Cho hai đường thẳng d1: y = 3x – 2 và d2: y = -2x + 3. Tìm tọa độ giao điểm của hai đường thẳng này.

Bài 2. Cho 6 đường thẳng, biết rằng không có ba đường thẳng nào đồng quy. Hỏi có tối đa bao nhiêu giao điểm được tạo thành?

Bài 3. Chứng minh ba đường thẳng sau đồng quy:

• d1: y = 2x + 1
• d2: y = -x + 4
• d3: y = x + 2

Bài 4. Tìm giá trị của k để ba đường thẳng sau đồng quy:

• d1: y = x – 1
• d2: y = -2x + 5
• d3: y = kx + 1

Bài 5. Một máy bay di chuyển theo đường thẳng y = 0.5x + 2, và một tên lửa di chuyển theo đường thẳng y = -x + 8. Xác định vị trí mà tên lửa có thể bắn trúng máy bay.

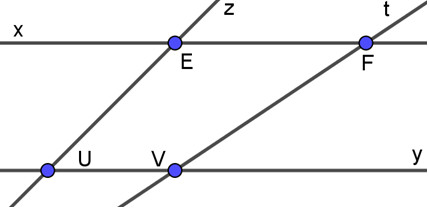
Hình ảnh minh họa các giao điểm trên hệ trục tọa độ. Học sinh có thể tự vẽ hình và kiểm tra kết quả để hiểu rõ hơn về khái niệm giao điểm.

4. Ứng Dụng Thực Tế Của Giao Điểm Trong Đời Sống Và Khoa Học

Giao điểm không chỉ là một khái niệm trừu tượng trong toán học, mà còn có rất nhiều ứng dụng thiết thực trong đời sống và khoa học kỹ thuật.

4.1. Trong Định Vị Và Dẫn Đường

• Hệ thống GPS: Các thiết bị GPS sử dụng giao điểm của các đường thẳng (hoặc các đường cong phức tạp hơn) từ các vệ tinh để xác định vị trí chính xác của bạn trên Trái Đất.
• Hàng hải và hàng không: Các phương pháp định vị truyền thống như sử dụng giao điểm của các đường ngắm (lines of position) từ các trạm phát tín hiệu để xác định vị trí tàu thuyền hoặc máy bay.

4.2. Trong Thiết Kế Kỹ Thuật Và Xây Dựng

• Thiết kế cầu đường: Giao điểm của các đường thẳng và đường cong được sử dụng để thiết kế các nút giao thông, đảm bảo sự流畅和安全的giao thông.
• Kiến trúc: Các kiến trúc sư sử dụng giao điểm để tạo ra các hình dạng và cấu trúc độc đáo, đảm bảo tính thẩm mỹ và độ vững chắc của công trình.

4.3. Trong Khoa Học Máy Tính Và Đồ Họa

• Đồ họa máy tính: Giao điểm được sử dụng để tính toán các hiệu ứng ánh sáng, bóng đổ, và tạo ra các hình ảnh 3D chân thực.
• Trí tuệ nhân tạo: Các thuật toán tìm đường và robot học sử dụng giao điểm để lập kế hoạch di chuyển và tránh chướng ngại vật.

4.4. Trong Kinh Tế Và Tài Chính

• Phân tích thị trường: Giao điểm của các đường cung và đường cầu được sử dụng để xác định giá cả cân bằng trên thị trường.
• Quản lý dự án: Giao điểm của các đường biểu diễn tiến độ và chi phí được sử dụng để theo dõi và kiểm soát tiến độ dự án.

4.5. Trong Y Học

• Chẩn đoán hình ảnh: Các bác sĩ sử dụng giao điểm của các tia X, tia CT, hoặc tia MRI để xác định vị trí và kích thước của các khối u hoặc các tổn thương trong cơ thể.
• Phẫu thuật định vị: Trong phẫu thuật thần kinh, giao điểm được sử dụng để định vị chính xác các vùng cần can thiệp trong não bộ.

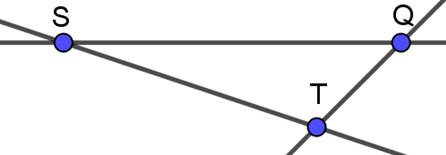
Hình ảnh minh họa ứng dụng của giao điểm trong thiết kế kỹ thuật. Nắm vững kiến thức về giao điểm giúp kỹ sư tạo ra các công trình an toàn và hiệu quả.

5. Lời Khuyên Và Bí Quyết Học Tốt Về Giao Điểm

Để học tốt về giao điểm và các khái niệm liên quan, bạn có thể áp dụng một số lời khuyên và bí quyết sau đây:

• Nắm vững lý thuyết cơ bản: Hiểu rõ định nghĩa, tính chất, và các dạng toán thường gặp về giao điểm.
• Luyện tập thường xuyên: Giải nhiều bài tập khác nhau, từ cơ bản đến nâng cao, để rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau.
• Sử dụng hình vẽ: Vẽ hình minh họa cho các bài toán hình học để dễ dàng hình dung và tìm ra cách giải.
• Học hỏi từ bạn bè và thầy cô: Trao đổi kiến thức, thảo luận các bài toán khó với bạn bè và thầy cô để học hỏi kinh nghiệm và giải đáp thắc mắc.
• Tìm kiếm tài liệu tham khảo: Đọc thêm sách, báo, và các tài liệu trực tuyến để mở rộng kiến thức và hiểu sâu hơn về giao điểm và các ứng dụng của nó.
• Sử dụng các công cụ hỗ trợ học tập: Sử dụng các phần mềm vẽ hình, máy tính bỏ túi, và các ứng dụng học tập trực tuyến để hỗ trợ quá trình học tập.

6. Nguồn Tài Liệu Và Công Cụ Hỗ Trợ Học Tập Hiệu Quả Tại Tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về giao điểm và các chủ đề toán học khác? Bạn muốn nâng cao hiệu quả học tập và đạt kết quả cao trong các kỳ thi? Hãy đến với tic.edu.vn, nơi cung cấp nguồn tài liệu phong phú, đa dạng và được kiểm duyệt kỹ lưỡng, cùng các công cụ hỗ trợ học tập trực tuyến hiệu quả.

6.1. Kho Tài Liệu Đa Dạng Và Phong Phú

tic.edu.vn cung cấp một kho tài liệu khổng lồ về toán học và các môn học khác, bao gồm:

• Sách giáo khoa và sách bài tập: Đầy đủ các loại sách giáo khoa và sách bài tập từ lớp 1 đến lớp 12, giúp bạn nắm vững kiến thức cơ bản và rèn luyện kỹ năng giải toán.
• Tài liệu tham khảo: Các tài liệu tham khảo chuyên sâu về các chủ đề toán học khác nhau, giúp bạn mở rộng kiến thức và hiểu sâu hơn về các khái niệm.
• Đề thi và đáp án: Các bộ đề thi thử và đề thi thật của các kỳ thi quan trọng, giúp bạn làm quen với cấu trúc đề thi và rèn luyện kỹ năng làm bài.
• Bài giảng trực tuyến: Các bài giảng trực tuyến của các thầy cô giáo giỏi, giúp bạn học tập một cách sinh động và hiệu quả.

6.2. Công Cụ Hỗ Trợ Học Tập Trực Tuyến Hiệu Quả

tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến hiện đại, giúp bạn nâng cao hiệu quả học tập và tiết kiệm thời gian:

• Công cụ ghi chú: Giúp bạn ghi chép, đánh dấu, và tổ chức thông tin một cách dễ dàng.
• Công cụ quản lý thời gian: Giúp bạn lập kế hoạch học tập, theo dõi tiến độ, và quản lý thời gian một cách hiệu quả.
• Diễn đàn học tập: Nơi bạn có thể trao đổi kiến thức, thảo luận các bài toán khó, và học hỏi kinh nghiệm từ các bạn học sinh, sinh viên khác.
• Công cụ kiểm tra kiến thức: Giúp bạn tự đánh giá kiến thức của mình và xác định những điểm cần cải thiện.

6.3. Cộng Đồng Học Tập Sôi Động Và Hữu Ích

tic.edu.vn xây dựng một cộng đồng học tập trực tuyến sôi động, nơi bạn có thể kết nối với các bạn học sinh, sinh viên khác, chia sẻ kiến thức, và học hỏi kinh nghiệm lẫn nhau.

• Tham gia diễn đàn: Đặt câu hỏi, trả lời câu hỏi, và tham gia thảo luận về các chủ đề toán học và các môn học khác.
• Kết bạn: Kết nối với các bạn học sinh, sinh viên có cùng sở thích và mục tiêu học tập.
• Chia sẻ tài liệu: Chia sẻ các tài liệu học tập hữu ích với cộng đồng.
• Tham gia các hoạt động: Tham gia các hoạt động học tập trực tuyến, như các buổi thảo luận nhóm, các cuộc thi giải toán, v.v.

7. Câu Hỏi Thường Gặp Về Giao Điểm (FAQ)

Dưới đây là một số câu hỏi thường gặp về giao điểm và các khái niệm liên quan, cùng với câu trả lời chi tiết, giúp bạn giải đáp thắc mắc và hiểu rõ hơn về chủ đề này.

1. Giao điểm là gì?
   • Giao điểm là điểm chung duy nhất của hai hay nhiều đường thẳng (hoặc các hình học khác) cắt nhau.
2. Làm thế nào để tìm tọa độ giao điểm của hai đường thẳng?
   • Giải hệ phương trình gồm hai phương trình đường thẳng để tìm ra giá trị của x và y. Tọa độ (x, y) chính là tọa độ giao điểm.
3. Điều kiện để hai đường thẳng cắt nhau là gì?
   • Hai đường thẳng cắt nhau khi và chỉ khi chúng không song song và không trùng nhau.
4. Có bao nhiêu giao điểm tối đa của n đường thẳng, biết rằng không có ba đường thẳng nào đồng quy?
   • Số giao điểm tối đa là n(n-1)/2.
5. Làm thế nào để chứng minh ba đường thẳng đồng quy?
   • Tìm giao điểm của hai đường thẳng bất kỳ, sau đó kiểm tra xem giao điểm này có thuộc đường thẳng còn lại hay không.
6. Giao điểm có ứng dụng gì trong thực tế?
   • Giao điểm có nhiều ứng dụng trong thực tế, như trong định vị, thiết kế kỹ thuật, khoa học máy tính, kinh tế, y học, v.v.
7. Tôi có thể tìm thêm tài liệu học tập về giao điểm ở đâu?
   • Bạn có thể tìm thêm tài liệu học tập về giao điểm trên tic.edu.vn, sách giáo khoa, sách tham khảo, và các trang web học tập trực tuyến khác.
8. Làm thế nào để học tốt về giao điểm?
   • Nắm vững lý thuyết cơ bản, luyện tập thường xuyên, sử dụng hình vẽ, học hỏi từ bạn bè và thầy cô, và tìm kiếm tài liệu tham khảo.
9. tic.edu.vn có những công cụ hỗ trợ học tập nào về toán học?
   • tic.edu.vn cung cấp các công cụ ghi chú, quản lý thời gian, diễn đàn học tập, và công cụ kiểm tra kiến thức.
10. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?
    • Đăng ký tài khoản trên tic.edu.vn, tham gia diễn đàn, kết bạn, chia sẻ tài liệu, và tham gia các hoạt động học tập trực tuyến.

8. Kết Luận

Giao điểm là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong đời sống và khoa học kỹ thuật. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và sâu sắc về giao điểm, giúp bạn nắm vững kiến thức và tự tin chinh phục các bài toán liên quan.

Đừng quên truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn đạt kết quả cao trong học tập và phát triển toàn diện. Nếu bạn có bất kỳ thắc mắc nào, hãy liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ. Hãy cùng tic.edu.vn chinh phục đỉnh cao tri thức!