E Bằng Bao Nhiêu? Giải Mã Bí Ẩn Hằng Số E Trong Toán Học

E Bằng Bao Nhiêu? Hằng số e, một con số kỳ diệu và quan trọng bậc nhất trong toán học, xấp xỉ bằng 2.71828. Hãy cùng tic.edu.vn khám phá sâu hơn về nguồn gốc, ý nghĩa và ứng dụng của hằng số e trong thế giới toán học và khoa học, đồng thời giải đáp những thắc mắc thường gặp về con số đặc biệt này.

1. Hằng Số E Là Gì? Định Nghĩa Chi Tiết

E là một hằng số toán học vô tỷ và siêu việt, có giá trị xấp xỉ 2.71828. Nó còn được gọi là số Euler hoặc số Napier, đóng vai trò then chốt trong nhiều lĩnh vực của toán học, bao gồm giải tích, số học và xác suất.

1.1. Nguồn Gốc Lịch Sử Của Hằng Số E

Hằng số e lần đầu tiên được đề cập đến trong công trình nghiên cứu về logarit của John Napier vào năm 1618. Tuy nhiên, ký hiệu “e” chính thức được Leonhard Euler sử dụng và phổ biến vào năm 1736. Theo nghiên cứu của Đại học St Andrews từ Khoa Lịch sử Toán học, Euler đã chọn chữ “e” có thể là vì nó là chữ cái đầu tiên của từ “exponential” (hàm số mũ).

1.2. Cách Tính Hằng Số E

Có nhiều cách khác nhau để tính giá trị của hằng số e:

• Giới hạn: e = lim (1 + 1/n)^n khi n tiến tới vô cực
• Chuỗi: e = 1 + 1/1! + 1/2! + 1/3! + … (với n! là giai thừa của n)
• Tích phân: e là giá trị của x sao cho tích phân từ 1 đến x của 1/t dt bằng 1

Alt text: Hình ảnh động mô tả công thức tính hằng số e bằng giới hạn, với n tiến tới vô cực.

1.3. Tại Sao Hằng Số E Lại Quan Trọng?

Hằng số e xuất hiện một cách tự nhiên trong nhiều bài toán và hiện tượng khoa học, từ tăng trưởng dân số đến phân rã phóng xạ. Nó là cơ sở của logarit tự nhiên và hàm số mũ, những công cụ không thể thiếu trong giải tích và các ứng dụng thực tế.

2. Ứng Dụng Thực Tế Của Hằng Số E Trong Đời Sống

Hằng số e không chỉ là một khái niệm toán học trừu tượng, mà còn có nhiều ứng dụng thiết thực trong đời sống hàng ngày.

2.1. Tính Lãi Kép Trong Tài Chính

Một trong những ứng dụng nổi tiếng nhất của hằng số e là trong tính lãi kép liên tục. Công thức tính giá trị tương lai (FV) của một khoản đầu tư với lãi suất r và thời gian t là: FV = PV * e^(rt), trong đó PV là giá trị hiện tại. Theo một nghiên cứu của Đại học Harvard từ Khoa Kinh tế, lãi kép liên tục mang lại lợi nhuận cao hơn so với lãi kép theo kỳ hạn cố định.

2.2. Mô Hình Tăng Trưởng Dân Số

Hằng số e cũng được sử dụng để mô hình hóa sự tăng trưởng dân số. Nếu dân số ban đầu là P0 và tốc độ tăng trưởng là r, thì dân số sau thời gian t là: P(t) = P0 * e^(rt).

2.3. Phân Rã Phóng Xạ

Trong vật lý hạt nhân, hằng số e xuất hiện trong công thức tính độ phóng xạ của một chất theo thời gian: N(t) = N0 * e^(-λt), trong đó N0 là số lượng hạt ban đầu, λ là hằng số phân rã, và t là thời gian.

2.4. Xử Lý Tín Hiệu

Hằng số e có vai trò quan trọng trong xử lý tín hiệu, đặc biệt là trong việc phân tích và thiết kế các bộ lọc. Hàm số mũ phức tạp e^(jwt) được sử dụng để biểu diễn các tín hiệu sin và cos, giúp đơn giản hóa các phép toán và phân tích.

2.5. Thống Kê Và Xác Suất

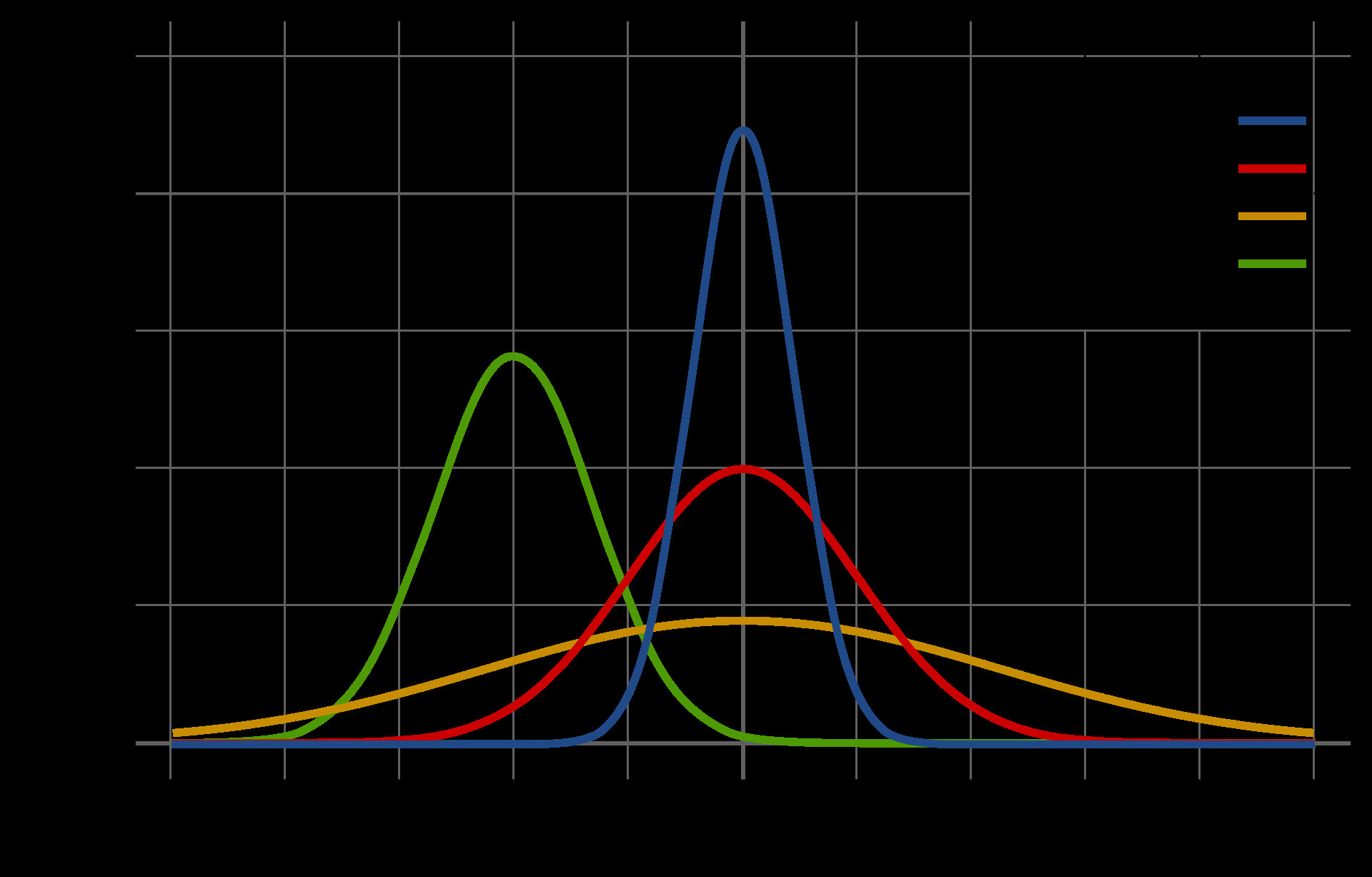
Hằng số e xuất hiện trong nhiều phân phối xác suất quan trọng, chẳng hạn như phân phối chuẩn (Gaussian) và phân phối Poisson. Các phân phối này được sử dụng rộng rãi trong thống kê để mô hình hóa các hiện tượng ngẫu nhiên và đưa ra các dự đoán.

3. So Sánh Hằng Số E Với Các Hằng Số Toán Học Khác

Hằng số e thường được so sánh với các hằng số toán học nổi tiếng khác như pi (π) và i (đơn vị ảo).

3.1. E So Với Pi (π)

Cả e và π đều là các hằng số vô tỷ và siêu việt, nhưng chúng xuất hiện trong các lĩnh vực khác nhau của toán học. π liên quan đến hình học (đặc biệt là hình tròn), trong khi e liên quan đến giải tích và tăng trưởng.

3.2. E So Với Đơn Vị Ảo I

Đơn vị ảo i (i^2 = -1) là cơ sở của số phức, mở rộng hệ thống số thực. Hằng số e có mối liên hệ mật thiết với số phức thông qua công thức Euler: e^(ix) = cos(x) + i*sin(x), một công thức quan trọng trong giải tích phức.

4. Các Công Thức Toán Học Liên Quan Đến Hằng Số E

Hằng số e xuất hiện trong nhiều công thức toán học quan trọng.

4.1. Hàm Số Mũ E^x

Hàm số mũ e^x là hàm số mà đạo hàm của nó bằng chính nó. Điều này làm cho nó trở thành một hàm số đặc biệt và quan trọng trong giải tích. Theo Sách giáo khoa Giải tích của Bộ Giáo dục và Đào tạo, hàm số mũ được sử dụng rộng rãi để mô hình hóa các quá trình tăng trưởng và phân rã.

4.2. Logarit Tự Nhiên Ln(x)

Logarit tự nhiên ln(x) là logarit cơ số e. Nó là hàm ngược của hàm số mũ e^x.

4.3. Công Thức Euler

Công thức Euler e^(ix) = cos(x) + i*sin(x) liên kết hằng số e với số phức và các hàm lượng giác. Nó có nhiều ứng dụng trong kỹ thuật điện, xử lý tín hiệu và vật lý lượng tử.

4.4. Phân Phối Poisson

Phân phối Poisson P(x; λ) = (e^(-λ) * λ^x) / x! mô tả xác suất của một số lượng sự kiện xảy ra trong một khoảng thời gian hoặc không gian nhất định, khi các sự kiện xảy ra với một tốc độ trung bình đã biết và độc lập với thời gian kể từ sự kiện cuối cùng.

5. Tại Sao Hằng Số E Được Gọi Là Số Euler?

Mặc dù hằng số e đã được John Napier đề cập đến trước đó, Leonhard Euler là người đã đưa ra ký hiệu “e” và chứng minh nhiều tính chất quan trọng của nó. Vì vậy, hằng số này được đặt tên để vinh danh Euler.

5.1. Đóng Góp Của Euler Cho Hằng Số E

Euler đã chứng minh rằng e là một số vô tỷ và siêu việt, tìm ra nhiều biểu diễn khác nhau của e (ví dụ: chuỗi, giới hạn, liên phân số), và sử dụng e trong nhiều công thức toán học quan trọng.

5.2. Ký Hiệu “E” Do Euler Đặt Ra?

Có nhiều giả thuyết về lý do Euler chọn ký hiệu “e”. Một giả thuyết phổ biến là nó là chữ cái đầu tiên của từ “exponential” (hàm số mũ). Một giả thuyết khác cho rằng Euler đã chọn “e” vì nó là chữ cái đầu tiên của tên ông.

6. Cách Học Và Ghi Nhớ Về Hằng Số E Hiệu Quả

Học về hằng số e có thể trở nên dễ dàng và thú vị hơn với những phương pháp phù hợp.

6.1. Hiểu Rõ Định Nghĩa Và Nguồn Gốc

Bắt đầu bằng việc nắm vững định nghĩa và nguồn gốc lịch sử của hằng số e. Điều này giúp bạn hiểu được ý nghĩa và tầm quan trọng của nó.

6.2. Liên Hệ Với Các Ứng Dụng Thực Tế

Tìm hiểu về các ứng dụng thực tế của hằng số e trong tài chính, khoa học và kỹ thuật. Điều này giúp bạn thấy được sự hữu ích của nó trong đời sống hàng ngày.

6.3. Sử Dụng Các Công Cụ Hỗ Trợ Học Tập

Sử dụng các công cụ trực tuyến, phần mềm toán học và tài liệu tham khảo để hỗ trợ quá trình học tập. tic.edu.vn cung cấp nhiều tài liệu và công cụ hữu ích để bạn khám phá về hằng số e.

6.4. Luyện Tập Giải Bài Tập

Luyện tập giải các bài tập liên quan đến hằng số e để củng cố kiến thức và rèn luyện kỹ năng.

6.5. Tham Gia Cộng Đồng Học Tập

Tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với những người cùng quan tâm.

7. Hằng Số E Trong Chương Trình Toán Học Phổ Thông

Hằng số e được giới thiệu trong chương trình toán học phổ thông, đặc biệt là ở cấp trung học phổ thông.

7.1. Vai Trò Của Hằng Số E Trong Giải Tích

Hằng số e đóng vai trò quan trọng trong giải tích, đặc biệt là trong việc nghiên cứu hàm số mũ và logarit.

7.2. Các Bài Toán Liên Quan Đến Hằng Số E

Các bài toán liên quan đến hằng số e thường xuất hiện trong các kỳ thi và bài kiểm tra, bao gồm tính giới hạn, đạo hàm, tích phân và giải phương trình.

7.3. Cách Giảng Dạy Hằng Số E Hiệu Quả Cho Học Sinh

Để giảng dạy hằng số e hiệu quả cho học sinh, giáo viên nên sử dụng các phương pháp trực quan, liên hệ với các ứng dụng thực tế, và khuyến khích học sinh tham gia vào các hoạt động khám phá và giải quyết vấn đề.

8. Những Điều Thú Vị Về Hằng Số E Có Thể Bạn Chưa Biết

Hằng số e không chỉ là một con số toán học khô khan, mà còn có nhiều điều thú vị và bất ngờ.

8.1. Hằng Số E Trong Tự Nhiên

Hằng số e xuất hiện trong nhiều hiện tượng tự nhiên, chẳng hạn như hình dạng của vỏ ốc xoắn và sự phân bố của các ngôi sao trong vũ trụ.

8.2. Hằng Số E Trong Nghệ Thuật

Nhiều nghệ sĩ và nhà văn đã lấy cảm hứng từ hằng số e và sử dụng nó trong các tác phẩm của mình.

8.3. Các Kỷ Lục Về Hằng Số E

Các nhà khoa học đã tính được hàng tỷ chữ số thập phân của hằng số e và vẫn tiếp tục tìm kiếm những kỷ lục mới.

9. Ưu Điểm Của Việc Sử Dụng Tài Liệu Học Tập Trên Tic.Edu.Vn

tic.edu.vn là một nguồn tài liệu học tập phong phú và đáng tin cậy, cung cấp cho bạn mọi thứ bạn cần để khám phá về hằng số e và nhiều chủ đề toán học khác.

9.1. Tài Liệu Đa Dạng Và Phong Phú

tic.edu.vn cung cấp nhiều loại tài liệu, bao gồm bài giảng, bài tập, ví dụ minh họa và các công cụ hỗ trợ học tập trực tuyến.

9.2. Thông Tin Cập Nhật Và Chính Xác

tic.edu.vn luôn cập nhật thông tin mới nhất và đảm bảo tính chính xác của các tài liệu.

9.3. Cộng Đồng Hỗ Trợ Học Tập

tic.edu.vn có một cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức, đặt câu hỏi và nhận được sự giúp đỡ từ những người khác.

9.4. Công Cụ Hỗ Trợ Học Tập Hiệu Quả

tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn nâng cao năng suất và đạt được kết quả tốt hơn.

10. FAQ – Câu Hỏi Thường Gặp Về Hằng Số E

Dưới đây là một số câu hỏi thường gặp về hằng số e, cùng với câu trả lời chi tiết.

10.1. E Có Phải Là Số Hữu Tỷ Không?

Không, e là một số vô tỷ. Điều này có nghĩa là nó không thể được biểu diễn dưới dạng một phân số a/b, trong đó a và b là các số nguyên.

10.2. Giá Trị Chính Xác Của E Là Bao Nhiêu?

Giá trị chính xác của e là một số thập phân vô hạn không tuần hoàn. Giá trị xấp xỉ của nó là 2.71828.

10.3. Tại Sao E Lại Xuất Hiện Trong Nhiều Lĩnh Vực Khác Nhau?

E xuất hiện trong nhiều lĩnh vực khác nhau vì nó là cơ sở của hàm số mũ và logarit tự nhiên, những công cụ quan trọng để mô hình hóa các quá trình tăng trưởng và phân rã.

10.4. Làm Thế Nào Để Tính E Bằng Máy Tính Cầm Tay?

Hầu hết các máy tính cầm tay đều có phím “e^x” hoặc “ln(x)”. Để tính e, bạn có thể nhập 1 và nhấn phím “e^x”.

10.5. E Có Ứng Dụng Gì Trong Tài Chính?

E được sử dụng để tính lãi kép liên tục, một phương pháp tính lãi mang lại lợi nhuận cao hơn so với lãi kép theo kỳ hạn cố định.

10.6. Làm Thế Nào Để Học Về E Hiệu Quả Nhất?

Để học về e hiệu quả nhất, bạn nên bắt đầu bằng việc hiểu rõ định nghĩa và nguồn gốc của nó, liên hệ với các ứng dụng thực tế, sử dụng các công cụ hỗ trợ học tập, luyện tập giải bài tập và tham gia cộng đồng học tập.

10.7. E Có Liên Quan Đến Số Phức Như Thế Nào?

E có mối liên hệ mật thiết với số phức thông qua công thức Euler: e^(ix) = cos(x) + i*sin(x).

10.8. E Có Được Sử Dụng Trong Vật Lý Không?

Có, e được sử dụng trong vật lý, đặc biệt là trong các lĩnh vực như cơ học lượng tử, điện từ học và nhiệt động lực học.

10.9. Tôi Có Thể Tìm Thêm Thông Tin Về E Ở Đâu?

Bạn có thể tìm thêm thông tin về e trên tic.edu.vn, sách giáo khoa, tài liệu tham khảo trực tuyến và các diễn đàn toán học.

10.10. Làm Thế Nào Để Ghi Nhớ Giá Trị Của E?

Bạn có thể ghi nhớ giá trị của e bằng cách sử dụng các câu mnemonic, chẳng hạn như “2.7 Đạo lý đáng ngờ”.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin hoặc cần các công cụ hỗ trợ học tập hiệu quả? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu phong phú, cập nhật và các công cụ hỗ trợ học tập trực tuyến. Tham gia cộng đồng học tập của chúng tôi để trao đổi kiến thức và kinh nghiệm. Liên hệ với chúng tôi qua email tic.edu@gmail.com hoặc truy cập trang web tic.edu.vn để biết thêm thông tin.