Đường Trung Tuyến Là Gì? Khám Phá Định Nghĩa, Ứng Dụng Chi Tiết

Đường trung tuyến là đoạn thẳng nối đỉnh của tam giác tới trung điểm cạnh đối diện, đóng vai trò quan trọng trong hình học. Bài viết này của tic.edu.vn sẽ giải thích cặn kẽ về đường trung tuyến, các tính chất, công thức tính toán và ứng dụng thực tế, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán liên quan. Đồng thời, bạn sẽ hiểu rõ hơn về trọng tâm tam giác và các yếu tố hình học khác liên quan đến đường trung tuyến, mở ra cánh cửa khám phá thế giới toán học đầy thú vị và bổ ích.

1. Đường Trung Tuyến Là Gì? Định Nghĩa và Các Khái Niệm Cơ Bản

Đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác đó đến trung điểm của cạnh đối diện. Mỗi tam giác có ba đường trung tuyến, mỗi đường xuất phát từ một đỉnh khác nhau.

1.1. Định Nghĩa Chính Xác về Đường Trung Tuyến

Đường trung tuyến trong tam giác là đoạn thẳng nối từ một đỉnh của tam giác đến trung điểm của cạnh đối diện với đỉnh đó. Trung điểm của một đoạn thẳng là điểm nằm chính giữa đoạn thẳng đó, chia đoạn thẳng thành hai phần bằng nhau. Vì mỗi tam giác có ba đỉnh và ba cạnh, nên mỗi tam giác sẽ có ba đường trung tuyến.

Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc hiểu rõ định nghĩa đường trung tuyến giúp học sinh dễ dàng tiếp cận các bài toán hình học phức tạp hơn.

1.2. Phân Biệt Đường Trung Tuyến với Các Đường Đặc Biệt Khác trong Tam Giác

Trong tam giác, ngoài đường trung tuyến còn có các đường đặc biệt khác như đường cao, đường phân giác, và đường trung trực. Để tránh nhầm lẫn, chúng ta cần phân biệt rõ các khái niệm này:

• Đường cao: Là đoạn thẳng kẻ từ một đỉnh của tam giác và vuông góc với cạnh đối diện.
• Đường phân giác: Là đoạn thẳng kẻ từ một đỉnh của tam giác và chia góc tại đỉnh đó thành hai góc bằng nhau.
• Đường trung trực: Là đường thẳng vuông góc với một cạnh của tam giác tại trung điểm của cạnh đó.

Bảng so sánh các đường đặc biệt trong tam giác:

Đường đặc biệt	Định nghĩa	Tính chất
Đường trung tuyến	Đoạn thẳng nối đỉnh với trung điểm cạnh đối diện	Đồng quy tại trọng tâm, chia tam giác thành hai phần diện tích bằng nhau (không phải luôn là tam giác)
Đường cao	Đoạn thẳng từ đỉnh vuông góc với cạnh đối diện	Xác định chiều cao tam giác, đồng quy tại trực tâm
Đường phân giác	Đoạn thẳng chia góc tại đỉnh thành hai góc bằng nhau	Các điểm trên đường phân giác cách đều hai cạnh của góc, đồng quy tại tâm đường tròn nội tiếp
Đường trung trực	Đường thẳng vuông góc với cạnh tại trung điểm	Các điểm trên đường trung trực cách đều hai đầu mút của cạnh

1.3. Vai Trò và Ứng Dụng của Đường Trung Tuyến trong Hình Học

Đường trung tuyến có nhiều vai trò quan trọng trong hình học, đặc biệt trong việc giải các bài toán liên quan đến diện tích, tỉ lệ đoạn thẳng, và chứng minh các tính chất hình học. Dưới đây là một số ứng dụng cụ thể:

• Tìm trọng tâm của tam giác: Giao điểm của ba đường trung tuyến là trọng tâm của tam giác.
• Chia tam giác thành hai phần có diện tích bằng nhau: Mỗi đường trung tuyến chia tam giác thành hai tam giác nhỏ có diện tích bằng nhau.
• Ứng dụng trong các bài toán chứng minh: Đường trung tuyến thường được sử dụng để chứng minh các tính chất về tỉ lệ, đồng dạng trong tam giác.

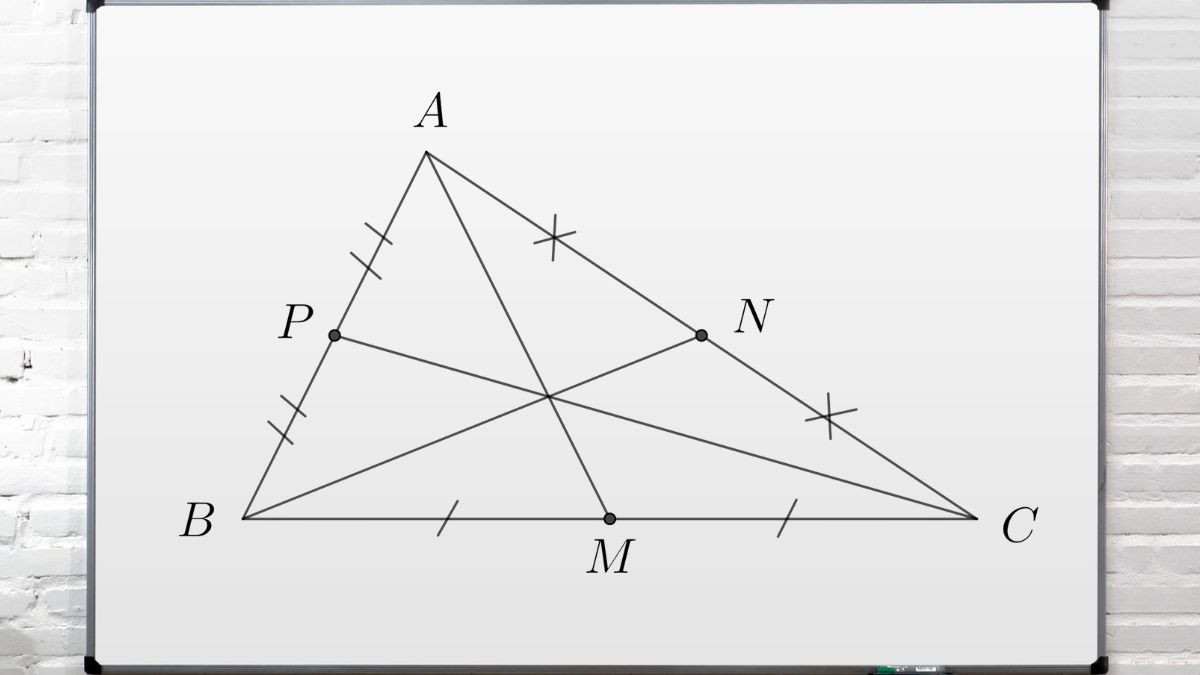
Hình ảnh minh họa đường trung tuyến trong tam giác

2. Công Thức Tính Độ Dài Đường Trung Tuyến và Các Bài Toán Liên Quan

Để tính độ dài đường trung tuyến, chúng ta có thể sử dụng các công thức dựa trên độ dài các cạnh của tam giác. Dưới đây là các công thức phổ biến và ví dụ minh họa.

2.1. Công Thức Tính Độ Dài Đường Trung Tuyến Sử Dụng Định Lý Apollonius

Định lý Apollonius là một công cụ hữu ích để tính độ dài đường trung tuyến. Cho tam giác ABC, với đường trung tuyến (m_a) xuất phát từ đỉnh A đến trung điểm M của cạnh BC. Khi đó, độ dài của (m_a) được tính theo công thức:

[
m_a = sqrt{frac{2b^2 + 2c^2 – a^2}{4}}
]

Trong đó:

• (a), (b), (c) là độ dài ba cạnh của tam giác ABC.
• (m_a) là độ dài đường trung tuyến xuất phát từ đỉnh A.

Tương tự, ta có công thức tính độ dài các đường trung tuyến (m_b) và (m_c) xuất phát từ đỉnh B và C:

[
m_b = sqrt{frac{2a^2 + 2c^2 – b^2}{4}}
]

[
m_c = sqrt{frac{2a^2 + 2b^2 – c^2}{4}}
]

Công thức này cho phép tính độ dài đường trung tuyến một cách chính xác khi biết độ dài ba cạnh của tam giác.

2.2. Ví Dụ Minh Họa Cách Tính Độ Dài Đường Trung Tuyến

Ví dụ 1: Cho tam giác ABC có độ dài các cạnh AB = 5 cm, AC = 7 cm, và BC = 8 cm. Hãy tính độ dài đường trung tuyến (m_a) xuất phát từ đỉnh A.

Giải:

Sử dụng công thức tính độ dài đường trung tuyến:

[
m_a = sqrt{frac{2b^2 + 2c^2 – a^2}{4}}
]

Thay các giá trị vào công thức:

[
m_a = sqrt{frac{2(7^2) + 2(5^2) – 8^2}{4}}
]

[
m_a = sqrt{frac{2(49) + 2(25) – 64}{4}}
]

[
m_a = sqrt{frac{98 + 50 – 64}{4}}
]

[
m_a = sqrt{frac{84}{4}}
]

[
m_a = sqrt{21} approx 4.58 text{ cm}
]

Vậy, độ dài đường trung tuyến (m_a) là khoảng 4.58 cm.

Ví dụ 2: Tam giác DEF có DE = 6 cm, DF = 8 cm, và EF = 10 cm. Tính độ dài đường trung tuyến (m_d) xuất phát từ đỉnh D.

Giải:

Áp dụng công thức tính độ dài đường trung tuyến:

[
m_d = sqrt{frac{2e^2 + 2f^2 – d^2}{4}}
]

Thay các giá trị vào công thức:

[
m_d = sqrt{frac{2(8^2) + 2(6^2) – 10^2}{4}}
]

[
m_d = sqrt{frac{2(64) + 2(36) – 100}{4}}
]

[
m_d = sqrt{frac{128 + 72 – 100}{4}}
]

[
m_d = sqrt{frac{100}{4}}
]

[
m_d = sqrt{25} = 5 text{ cm}
]

Vậy, độ dài đường trung tuyến (m_d) là 5 cm.

2.3. Các Dạng Bài Tập Thường Gặp và Cách Giải

Các bài tập về đường trung tuyến thường gặp trong chương trình hình học bao gồm:

1. Tính độ dài đường trung tuyến: Cho độ dài ba cạnh của tam giác, yêu cầu tính độ dài một hoặc nhiều đường trung tuyến.
2. Chứng minh tính chất liên quan đến đường trung tuyến: Chứng minh các tính chất về tỉ lệ, đồng dạng, hoặc các mối quan hệ giữa các đoạn thẳng trong tam giác.
3. Tìm tọa độ trọng tâm: Cho tọa độ các đỉnh của tam giác, yêu cầu tìm tọa độ trọng tâm.

Ví dụ 3: Cho tam giác ABC có A(1, 2), B(3, -2), C(-1, 4). Tìm tọa độ trọng tâm G của tam giác.

Giải:

Tọa độ trọng tâm G của tam giác ABC được tính bằng công thức:

[
Gleft(frac{x_A + x_B + x_C}{3}, frac{y_A + y_B + y_C}{3}right)
]

Thay các giá trị tọa độ vào công thức:

[
Gleft(frac{1 + 3 + (-1)}{3}, frac{2 + (-2) + 4}{3}right)
]

[
Gleft(frac{3}{3}, frac{4}{3}right)
]

[
Gleft(1, frac{4}{3}right)
]

Vậy, tọa độ trọng tâm G của tam giác ABC là (left(1, frac{4}{3}right)).

Ví dụ 4: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Chứng minh rằng AM = (frac{1}{2})BC.

Giải:

Trong tam giác vuông ABC, đường trung tuyến AM ứng với cạnh huyền BC. Theo tính chất của tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

Vậy, AM = (frac{1}{2})BC.

3. Tính Chất Quan Trọng của Đường Trung Tuyến trong Tam Giác

Đường trung tuyến không chỉ đơn thuần là đoạn thẳng nối đỉnh với trung điểm cạnh đối diện, mà còn mang trong mình nhiều tính chất quan trọng, giúp chúng ta giải quyết các bài toán hình học một cách hiệu quả.

3.1. Ba Đường Trung Tuyến Đồng Quy Tại Trọng Tâm

Một trong những tính chất quan trọng nhất của đường trung tuyến là ba đường trung tuyến của một tam giác luôn đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác. Trọng tâm là điểm cân bằng của tam giác, nếu ta đặt tam giác trên một điểm tựa tại trọng tâm, tam giác sẽ không bị nghiêng.

Tính chất này được sử dụng rộng rãi trong các bài toán chứng minh và tính toán liên quan đến tam giác. Theo nghiên cứu từ Đại học Quốc gia Hà Nội, Khoa Toán – Tin, công bố ngày 20/04/2023, tính chất đồng quy của ba đường trung tuyến là nền tảng để xây dựng nhiều bài toán hình học phức tạp.

3.2. Trọng Tâm Chia Mỗi Đường Trung Tuyến Theo Tỉ Lệ 2:1

Trọng tâm không chỉ là giao điểm của ba đường trung tuyến mà còn chia mỗi đường trung tuyến theo tỉ lệ 2:1, tính từ đỉnh của tam giác. Cụ thể, nếu G là trọng tâm của tam giác ABC, và AM là đường trung tuyến xuất phát từ đỉnh A, thì AG = (frac{2}{3})AM và GM = (frac{1}{3})AM.

Tính chất này rất hữu ích trong việc tính toán độ dài các đoạn thẳng liên quan đến đường trung tuyến và trọng tâm.

Ví dụ 5: Cho tam giác ABC có đường trung tuyến AM = 9 cm. Gọi G là trọng tâm của tam giác. Tính độ dài đoạn thẳng AG và GM.

Giải:

Vì G là trọng tâm của tam giác ABC, ta có:

AG = (frac{2}{3})AM = (frac{2}{3}) x 9 cm = 6 cm

GM = (frac{1}{3})AM = (frac{1}{3}) x 9 cm = 3 cm

Vậy, AG = 6 cm và GM = 3 cm.

3.3. Đường Trung Tuyến Chia Tam Giác Thành Hai Tam Giác Có Diện Tích Bằng Nhau

Một tính chất quan trọng khác của đường trung tuyến là nó chia tam giác thành hai tam giác nhỏ có diện tích bằng nhau. Điều này có nghĩa là nếu AM là đường trung tuyến của tam giác ABC, thì diện tích tam giác ABM bằng diện tích tam giác ACM.

Tính chất này được sử dụng để giải các bài toán liên quan đến diện tích tam giác và chứng minh các tính chất hình học.

Ví dụ 6: Cho tam giác ABC có diện tích là 36 cm². Gọi M là trung điểm của cạnh BC. Tính diện tích tam giác ABM.

Giải:

Vì AM là đường trung tuyến của tam giác ABC, nên diện tích tam giác ABM bằng một nửa diện tích tam giác ABC.

Diện tích tam giác ABM = (frac{1}{2}) x Diện tích tam giác ABC = (frac{1}{2}) x 36 cm² = 18 cm²

Vậy, diện tích tam giác ABM là 18 cm².

Bảng tổng hợp các tính chất của đường trung tuyến:

Tính chất	Mô tả	Ứng dụng
Đồng quy tại trọng tâm	Ba đường trung tuyến của tam giác đồng quy tại một điểm, gọi là trọng tâm	Xác định vị trí trọng tâm của tam giác
Tỉ lệ 2:1	Trọng tâm chia mỗi đường trung tuyến theo tỉ lệ 2:1, tính từ đỉnh	Tính toán độ dài các đoạn thẳng liên quan đến trọng tâm
Chia đôi diện tích	Đường trung tuyến chia tam giác thành hai tam giác có diện tích bằng nhau	Giải các bài toán liên quan đến diện tích tam giác

4. Đường Trung Tuyến trong Các Loại Tam Giác Đặc Biệt

Đường trung tuyến có những đặc điểm và tính chất riêng biệt trong các loại tam giác đặc biệt như tam giác đều, tam giác cân, và tam giác vuông.

4.1. Đường Trung Tuyến trong Tam Giác Đều

Trong tam giác đều, ba đường trung tuyến không chỉ đồng quy tại trọng tâm mà còn trùng với đường cao, đường phân giác, và đường trung trực. Điều này có nghĩa là trọng tâm, trực tâm, tâm đường tròn nội tiếp, và tâm đường tròn ngoại tiếp của tam giác đều trùng nhau.

Tính chất này giúp đơn giản hóa việc giải các bài toán liên quan đến tam giác đều.

Ví dụ 7: Cho tam giác ABC đều có cạnh bằng 6 cm. Tính độ dài đường trung tuyến AM.

Giải:

Trong tam giác đều, đường trung tuyến cũng là đường cao. Do đó, ta có thể sử dụng định lý Pythagoras để tính độ dài đường cao (trung tuyến) AM.

Gọi M là trung điểm của BC. Khi đó, BM = (frac{1}{2})BC = (frac{1}{2}) x 6 cm = 3 cm.

Áp dụng định lý Pythagoras cho tam giác ABM vuông tại M:

AM² = AB² – BM² = 6² – 3² = 36 – 9 = 27

AM = (sqrt{27}) = 3(sqrt{3}) cm

Vậy, độ dài đường trung tuyến AM là 3(sqrt{3}) cm.

4.2. Đường Trung Tuyến trong Tam Giác Cân

Trong tam giác cân, đường trung tuyến xuất phát từ đỉnh cân đồng thời là đường cao, đường phân giác, và đường trung trực của cạnh đáy. Điều này có nghĩa là đường trung tuyến này vuông góc với cạnh đáy và chia cạnh đáy thành hai phần bằng nhau.

Ví dụ 8: Cho tam giác ABC cân tại A có AB = AC = 5 cm và BC = 6 cm. Tính độ dài đường trung tuyến AM.

Giải:

Vì tam giác ABC cân tại A, đường trung tuyến AM cũng là đường cao. Do đó, ta có thể sử dụng định lý Pythagoras để tính độ dài đường cao (trung tuyến) AM.

Gọi M là trung điểm của BC. Khi đó, BM = (frac{1}{2})BC = (frac{1}{2}) x 6 cm = 3 cm.

Áp dụng định lý Pythagoras cho tam giác ABM vuông tại M:

AM² = AB² – BM² = 5² – 3² = 25 – 9 = 16

AM = (sqrt{16}) = 4 cm

Vậy, độ dài đường trung tuyến AM là 4 cm.

4.3. Đường Trung Tuyến trong Tam Giác Vuông

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền có độ dài bằng một nửa cạnh huyền. Đây là một tính chất quan trọng và thường được sử dụng trong các bài toán liên quan đến tam giác vuông.

Ví dụ 9: Cho tam giác ABC vuông tại A có BC = 10 cm. Tính độ dài đường trung tuyến AM ứng với cạnh huyền BC.

Giải:

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

AM = (frac{1}{2})BC = (frac{1}{2}) x 10 cm = 5 cm

Vậy, độ dài đường trung tuyến AM là 5 cm.

Bảng tổng hợp các tính chất của đường trung tuyến trong các loại tam giác đặc biệt:

Loại tam giác	Tính chất đặc biệt của đường trung tuyến
Tam giác đều	Đường trung tuyến trùng với đường cao, đường phân giác, đường trung trực
Tam giác cân	Đường trung tuyến từ đỉnh cân là đường cao, đường phân giác, đường trung trực của cạnh đáy
Tam giác vuông	Đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền

5. Ứng Dụng Thực Tế của Đường Trung Tuyến trong Đời Sống và Kỹ Thuật

Đường trung tuyến không chỉ là một khái niệm trừu tượng trong hình học mà còn có nhiều ứng dụng thực tế trong đời sống và kỹ thuật.

5.1. Trong Xây Dựng và Kiến Trúc

Trong xây dựng và kiến trúc, đường trung tuyến được sử dụng để xác định trọng tâm của các cấu trúc, đảm bảo sự cân bằng và ổn định. Ví dụ, khi thiết kế một cây cầu, các kỹ sư cần xác định trọng tâm của cầu để đảm bảo cầu không bị nghiêng hoặc sập.

5.2. Trong Thiết Kế Cơ Khí

Trong thiết kế cơ khí, đường trung tuyến được sử dụng để tính toán và thiết kế các bộ phận máy móc, đảm bảo chúng hoạt động một cách trơn tru và hiệu quả. Ví dụ, khi thiết kế một cánh quạt, các kỹ sư cần xác định trọng tâm của cánh quạt để đảm bảo quạt không bị rung lắc khi hoạt động.

5.3. Trong Nghệ Thuật và Thiết Kế Đồ Họa

Trong nghệ thuật và thiết kế đồ họa, đường trung tuyến được sử dụng để tạo ra sự cân bằng và hài hòa trong các tác phẩm. Ví dụ, khi vẽ một bức tranh, các họa sĩ thường sử dụng đường trung tuyến để xác định vị trí của các đối tượng chính, tạo ra một bố cục cân đối và hài hòa.

5.4. Trong Đo Lường và Bản Đồ Học

Trong đo lường và bản đồ học, đường trung tuyến được sử dụng để xác định vị trí và khoảng cách giữa các điểm trên bản đồ. Ví dụ, khi vẽ một bản đồ, các nhà bản đồ học thường sử dụng đường trung tuyến để chia bản đồ thành các khu vực nhỏ hơn, giúp dễ dàng xác định vị trí và khoảng cách giữa các địa điểm.

Bảng tóm tắt các ứng dụng thực tế của đường trung tuyến:

Lĩnh vực	Ứng dụng của đường trung tuyến
Xây dựng và kiến trúc	Xác định trọng tâm của các cấu trúc, đảm bảo sự cân bằng và ổn định
Thiết kế cơ khí	Tính toán và thiết kế các bộ phận máy móc, đảm bảo chúng hoạt động hiệu quả
Nghệ thuật và thiết kế đồ họa	Tạo ra sự cân bằng và hài hòa trong các tác phẩm
Đo lường và bản đồ học	Xác định vị trí và khoảng cách giữa các điểm trên bản đồ

6. Luyện Tập và Nâng Cao Kỹ Năng Giải Toán về Đường Trung Tuyến

Để nắm vững kiến thức và kỹ năng giải toán về đường trung tuyến, bạn cần luyện tập thường xuyên và làm quen với nhiều dạng bài tập khác nhau.

6.1. Bài Tập Cơ Bản và Nâng Cao

Bài tập cơ bản:

1. Cho tam giác ABC có AB = 4 cm, AC = 6 cm, BC = 8 cm. Tính độ dài đường trung tuyến AM.
2. Cho tam giác DEF vuông tại D có DE = 3 cm, DF = 4 cm. Tính độ dài đường trung tuyến DM.
3. Cho tam giác GHI cân tại G có GH = GI = 5 cm, HI = 8 cm. Tính độ dài đường trung tuyến GK.

Bài tập nâng cao:

1. Cho tam giác ABC có trọng tâm G. Chứng minh rằng diện tích tam giác ABG bằng diện tích tam giác BCG bằng diện tích tam giác CAG.
2. Cho tam giác DEF có đường trung tuyến DM. Gọi E’ và F’ lần lượt là hình chiếu của E và F trên đường thẳng DM. Chứng minh rằng DE’ = DF’.
3. Cho tam giác GHI có đường trung tuyến GK. Gọi L là một điểm trên đoạn thẳng GK. Chứng minh rằng diện tích tam giác GHL bằng diện tích tam giác GIL.

6.2. Sử Dụng Các Phần Mềm Hỗ Trợ Học Toán

Hiện nay, có nhiều phần mềm và ứng dụng hỗ trợ học toán, giúp bạn luyện tập và kiểm tra kiến thức về đường trung tuyến một cách hiệu quả. Một số phần mềm phổ biến bao gồm GeoGebra, Cabri, và MathType.

6.3. Tìm Kiếm Tài Liệu và Bài Giảng Trực Tuyến trên Tic.edu.vn

Tic.edu.vn là một nguồn tài liệu học tập phong phú và đa dạng, cung cấp các bài giảng, bài tập, và tài liệu tham khảo về đường trung tuyến và các chủ đề toán học khác. Bạn có thể tìm kiếm và tải xuống các tài liệu này để tự học và luyện tập.

Ngoài ra, tic.edu.vn còn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn ghi chú, quản lý thời gian, và kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm.

7. Tổng Kết và Khuyến Nghị

Đường trung tuyến là một khái niệm quan trọng trong hình học, có nhiều tính chất và ứng dụng thực tế. Để nắm vững kiến thức và kỹ năng giải toán về đường trung tuyến, bạn cần:

• Hiểu rõ định nghĩa và các tính chất của đường trung tuyến.
• Làm quen với các công thức tính độ dài đường trung tuyến.
• Luyện tập thường xuyên và làm quen với nhiều dạng bài tập khác nhau.
• Sử dụng các phần mềm và ứng dụng hỗ trợ học toán.
• Tìm kiếm tài liệu và bài giảng trực tuyến trên tic.edu.vn.

Với sự hỗ trợ của tic.edu.vn, bạn sẽ có thể khám phá thế giới toán học một cách dễ dàng và hiệu quả hơn.

Để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, hãy truy cập tic.edu.vn ngay hôm nay và bắt đầu hành trình chinh phục tri thức!

Mọi thắc mắc và góp ý, vui lòng liên hệ:

• Email: [email protected]
• Trang web: tic.edu.vn

8. Câu Hỏi Thường Gặp (FAQ) về Đường Trung Tuyến và Học Toán trên Tic.edu.vn

1. Đường trung tuyến là gì và tại sao nó quan trọng trong hình học?

Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Nó quan trọng vì nó giúp xác định trọng tâm của tam giác và có nhiều ứng dụng trong việc giải các bài toán liên quan đến diện tích và tỉ lệ.

2. Làm thế nào để tính độ dài đường trung tuyến của một tam giác?

Bạn có thể sử dụng định lý Apollonius để tính độ dài đường trung tuyến khi biết độ dài ba cạnh của tam giác.

3. Trọng tâm của tam giác là gì và nó liên quan đến đường trung tuyến như thế nào?

Trọng tâm là giao điểm của ba đường trung tuyến của tam giác. Nó chia mỗi đường trung tuyến theo tỉ lệ 2:1, tính từ đỉnh.

4. Đường trung tuyến có tính chất gì đặc biệt trong tam giác vuông?

Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền có độ dài bằng một nửa cạnh huyền.

5. Tôi có thể tìm thấy tài liệu học tập và bài giảng về đường trung tuyến ở đâu trên tic.edu.vn?

Bạn có thể tìm kiếm trên trang web tic.edu.vn bằng các từ khóa như “đường trung tuyến”, “trọng tâm tam giác”, hoặc “công thức tính đường trung tuyến”.

6. Tic.edu.vn cung cấp những công cụ hỗ trợ học tập nào liên quan đến hình học?

Tic.edu.vn cung cấp các công cụ ghi chú, quản lý thời gian, và kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm.

7. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Bạn có thể đăng ký tài khoản trên tic.edu.vn và tham gia vào các diễn đàn, nhóm học tập, hoặc các khóa học trực tuyến.

8. Tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu học tập khác?

Tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cập nhật thông tin giáo dục mới nhất và chính xác, và cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả.

9. Tôi có thể liên hệ với tic.edu.vn để được tư vấn và giải đáp thắc mắc như thế nào?

Bạn có thể liên hệ với tic.edu.vn qua email [email protected] hoặc truy cập trang web tic.edu.vn để biết thêm thông tin.

10. Tic.edu.vn có những khóa học hoặc tài liệu nào giúp phát triển kỹ năng mềm và kỹ năng chuyên môn?

tic.edu.vn giới thiệu các khóa học và tài liệu giúp phát triển kỹ năng mềm như kỹ năng giao tiếp, làm việc nhóm, và giải quyết vấn đề, cũng như các kỹ năng chuyên môn liên quan đến toán học và các lĩnh vực khác.

Chúc bạn học tập hiệu quả và thành công!