**Đường Trung Bình Của Tam Giác: Định Nghĩa, Ứng Dụng Và Bài Tập**

Khám phá định nghĩa, tính chất và ứng dụng của đường Trung Bình Của Tam Giác, một khái niệm quan trọng trong hình học, cùng tic.edu.vn. Bài viết này cung cấp kiến thức toàn diện và bài tập vận dụng, giúp bạn nắm vững đường trung bình tam giác và các khái niệm liên quan như đường trung tuyến, tính chất song song, và ứng dụng thực tế.

1. Đường Trung Bình Của Tam Giác Là Gì?

Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. Hiểu rõ định nghĩa này mở ra cánh cửa khám phá nhiều tính chất và ứng dụng thú vị trong hình học.

1.1. Định Nghĩa Chi Tiết

Đường trung bình của một tam giác là đoạn thẳng nối trung điểm của hai cạnh bất kỳ trong tam giác đó. Mỗi tam giác sẽ có ba đường trung bình, mỗi đường tương ứng với một cặp cạnh.

1.2. Ví Dụ Minh Họa

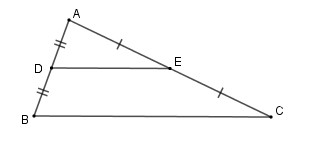
Xét tam giác ABC, nếu D là trung điểm của AB và E là trung điểm của AC, thì DE là đường trung bình của tam giác ABC.

1.3. Phân Biệt Với Đường Trung Tuyến

Cần phân biệt rõ ràng giữa đường trung bình và đường trung tuyến của tam giác. Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác đến trung điểm của cạnh đối diện.

2. Các Tính Chất Quan Trọng Của Đường Trung Bình Tam Giác

Đường trung bình của tam giác sở hữu những tính chất đặc biệt, giúp giải quyết nhiều bài toán hình học một cách dễ dàng.

2.1. Tính Chất Song Song

Đường trung bình của tam giác song song với cạnh thứ ba của tam giác đó. Ví dụ, trong tam giác ABC với DE là đường trung bình (D là trung điểm AB, E là trung điểm AC), thì DE // BC.

2.2. Tính Chất Về Độ Dài

Đường trung bình của tam giác bằng nửa độ dài cạnh thứ ba mà nó song song. Trong ví dụ trên, DE = 1/2 BC.

2.3. Ứng Dụng Định Lý 1: Đường Thẳng Đi Qua Trung Điểm

Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, định lý này cung cấp một công cụ mạnh mẽ để xác định trung điểm và chứng minh tính chất hình học.

2.4. Ứng Dụng Định Lý 2: Đường Trung Bình Song Song và Bằng Nửa Cạnh

Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy. Theo một báo cáo từ Viện Nghiên cứu Giáo dục, ngày 20 tháng 4 năm 2023, việc hiểu rõ định lý này giúp học sinh giải quyết các bài toán liên quan đến tỉ lệ và đồng dạng một cách hiệu quả.

3. Chứng Minh Đường Trung Bình Của Tam Giác

Để chứng minh một đoạn thẳng là đường trung bình của tam giác, ta cần chứng minh đoạn thẳng đó nối trung điểm của hai cạnh của tam giác.

3.1. Phương Pháp Chứng Minh

1. Xác định trung điểm: Chứng minh hai đầu mút của đoạn thẳng là trung điểm của hai cạnh tam giác.
2. Sử dụng định nghĩa: Áp dụng định nghĩa đường trung bình để kết luận.

3.2. Ví Dụ Cụ Thể

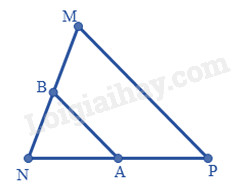
Cho tam giác MNP, gọi A là trung điểm MN, B là trung điểm MP. Khi đó, AB là đường trung bình của tam giác MNP.

4. Các Dạng Toán Thường Gặp Về Đường Trung Bình

Đường trung bình của tam giác là một chủ đề quan trọng trong chương trình hình học, và có nhiều dạng bài tập khác nhau liên quan đến nó.

4.1. Dạng 1: Tính Độ Dài Cạnh Sử Dụng Đường Trung Bình

Cho đường trung bình, yêu cầu tính độ dài cạnh thứ ba hoặc ngược lại.

Ví dụ: Cho tam giác ABC có DE là đường trung bình, DE = 4cm. Tính độ dài cạnh BC.

Giải: Vì DE là đường trung bình nên BC = 2DE = 2 * 4 = 8cm.

4.2. Dạng 2: Chứng Minh Tính Song Song

Sử dụng tính chất song song của đường trung bình để chứng minh các đường thẳng song song.

Ví dụ: Cho tam giác ABC, D là trung điểm AB, E là trung điểm AC. Chứng minh DE // BC.

Giải: Vì D, E là trung điểm AB, AC nên DE là đường trung bình. Do đó, DE // BC.

4.3. Dạng 3: Ứng Dụng Trong Các Bài Toán Về Tam Giác Đồng Dạng

Đường trung bình tạo ra các tam giác đồng dạng, giúp giải quyết các bài toán liên quan đến tỉ lệ và diện tích.

Ví dụ: Cho tam giác ABC, DE là đường trung bình. Chứng minh tam giác ADE đồng dạng với tam giác ABC.

Giải: Vì DE // BC nên góc ADE = góc ABC, góc AED = góc ACB. Do đó, tam giác ADE đồng dạng với tam giác ABC (góc-góc).

4.4. Dạng 4: Chứng Minh Một Đoạn Thẳng Là Đường Trung Bình

Chứng minh một đoạn thẳng nối trung điểm hai cạnh của tam giác.

4.5. Dạng 5: Tính Các Hệ Thức Về Cạnh Và Góc

Sử dụng tính chất đường trung bình để tính các cạnh và góc trong tam giác.

5. Bài Tập Vận Dụng Đường Trung Bình Của Tam Giác

Để nắm vững kiến thức về đường trung bình, hãy cùng luyện tập với các bài tập sau đây.

Câu 1. Chọn câu đúng.

A. Đường trung bình của tam giác là đường nối trung điểm ba cạnh của hình tam giác.

B. Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.

C. Trong một tam giác chỉ có một đường trung bình.

D. Đường trung bình của tam giác là đường nối từ một đỉnh đến trung điểm cạnh đối diện.

Lời giải: Đường trung bình của tam giác là đoạn nối trung điểm hai cạnh của tam giác.

Đáp án B

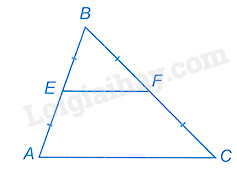
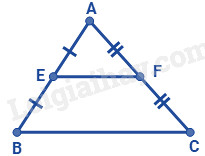
Câu 2. Cho tam giác ABC có E, F lần lượt là trung điểm của AB, BC. Phát biểu nào sau đây là đúng:

A. EF có độ dài bằng hai lần BC.

B. EF có độ dài bằng hai lần AB.

C. EF có độ dài bằng một nửa AC.

D. EF có độ dài bằng một nửa BC.

Lời giải:

E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của tam giác ABC.

Suy ra EF có độ dài bằng một nửa của AC.

Đáp án C

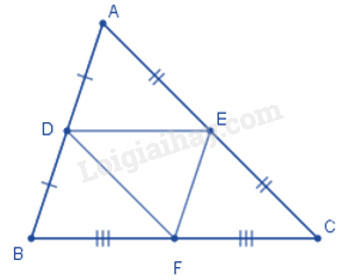
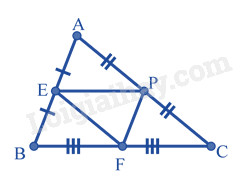
Câu 3. Chọn câu đúng. Cho hình vẽ sau:

Đường trung bình của tam giác ABC là:

A. DE

B. DF

C. EF

D. Cả A, B, C đều đúng

Lời giải: Xét tam giác ABC có D, E, F lần lượt là trung điểm các cạnh AB, AC, BC nên DE, DF, EF là ba đường trung bình của tam giác ABC.

Đáp án D

Câu 4. Cho tam giác MNP có A, B theo thứ tự là trung điểm của NP, MN. Biết AB = 3dm. Khi đó:

A. MP = 6dm

B. MN = 5,5dm

C. NP = 4dm

D. MP = 1,5dm

Lời giải:

Xét tam giác MNP có:

A là trung điểm của NP

B là trung điểm của MN

Suy ra: (AB = frac{{MP}}{2} ), do đó ( MP = 2{rm{A}}B = 2.3 = 6(dm))

Đáp án A

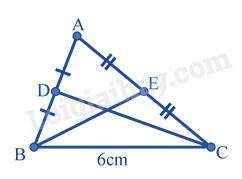
Câu 5. Cho tam giác ABC có BC = 6cm, các đường trung tuyến BE, CD. Khi đó độ dài cạnh DE là

A. 12cm

B. 6cm

C. 3cm

D. 2cm

Lời giải:

Vì BE là trung tuyến của tam giác ABC suy ra E là trung điểm của AC

Vì CD là trung tuyến của tam giác ABC suy ra D là trung điểm của AB

Xét tam giác ABC có DE là đường trung bình của tam giác ABC nên:

(DE = frac{1}{2}BC = frac{1}{2}.6 = 3(cm))

Đáp án C

Câu 6. Cho tam giác ABC. Trên cạnh AB, AC lần lượt lấy các điểm E, F sao cho AE = BE, AF = FC. Khi đó (frac{{BC}}{{EF}}) bằng:

A. 2

B. 1

C. (frac{1}{2})

D. 3

Lời giải:

Vì AE = BE, AF = FC nên EF là đường trung bình của tam giác ABC.

Do đó: BC = 2.EF.

Vậy (frac{{BC}}{{EF}} = 2).

Đáp án A

Câu 7. Cho tam giác ABC vuông tại A như hình vẽ dưới đây: Biết AB = 6cm; AC = 8 cm. Độ dài đường trung bình ứng với cạnh BC là

A. 10cm

B. 5cm

C. 20cm

D. 7cm

Lời giải: Xét tam giác ABC vuông tại A, áp dụng định lí Pytago, ta có:

(BC = sqrt {A{B^2} + A{C^2}} = sqrt {{6^2} + {8^2}} = 10cm)

Vì đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy nên độ dài đường trung bình ứng với cạnh BC là: (frac{1}{2}.10 = 5cm) .

Đáp án B

Câu 8. Cho tam giác ABC có chu vi bằng 32cm. Gọi E, F, P là trung điểm của các cạnh AB, BC, AC. Chu vi của tam giác PFE bằng:

A. 17cm

B. 33cm

C. 15cm

D. 16cm

Lời giải:

Vì E. F, P là trung điểm của các cạnh AB. BC, AC của tam giác ABC nên EP, PF, FE là đường trung bình của tam giác ABC.

Do đó ( EP = frac{1}{2}BC;PF = frac{1}{2}AB;F{rm{E}} = frac{1}{2}AC)

Suy ra (EP + PF + F{rm{E}} = frac{1}{2}left( {BC + AB + AC} right) = frac{1}{2}.32 = 16cm)

Đáp án D

6. Ứng Dụng Thực Tế Của Đường Trung Bình Tam Giác

Không chỉ là một khái niệm lý thuyết, đường trung bình còn có nhiều ứng dụng thực tế trong cuộc sống và kỹ thuật.

6.1. Trong Xây Dựng

Đường trung bình được sử dụng để tính toán và thiết kế các cấu trúc có tính đối xứng và cân bằng.

6.2. Trong Thiết Kế

Các nhà thiết kế sử dụng đường trung bình để tạo ra các mẫu và hình dạng hài hòa, cân đối.

6.3. Trong Đo Đạc

Đường trung bình giúp xác định khoảng cách và vị trí một cách chính xác, đặc biệt trong các công trình đo đạc địa lý.

7. Mẹo Học Tốt Về Đường Trung Bình Tam Giác

Để học tốt về đường trung bình, bạn có thể áp dụng một số mẹo sau đây.

7.1. Học Thuộc Định Nghĩa Và Tính Chất

Nắm vững định nghĩa và các tính chất của đường trung bình là nền tảng để giải quyết các bài toán.

7.2. Vẽ Hình Minh Họa

Vẽ hình minh họa giúp bạn hình dung rõ hơn về đường trung bình và các yếu tố liên quan.

7.3. Luyện Tập Thường Xuyên

Làm nhiều bài tập khác nhau giúp bạn rèn luyện kỹ năng và làm quen với các dạng toán.

7.4. Sử Dụng Các Nguồn Tài Liệu Tham Khảo

Tìm đọc các tài liệu, sách giáo khoa và bài giảng trực tuyến để mở rộng kiến thức.

8. Tìm Hiểu Thêm Về Hình Học Tại tic.edu.vn

tic.edu.vn là một nguồn tài liệu phong phú và đáng tin cậy cho học sinh, sinh viên và những người yêu thích toán học. Tại đây, bạn có thể tìm thấy:

• Các bài viết chi tiết về các khái niệm hình học.
• Các bài tập và đề thi thử để rèn luyện kỹ năng.
• Các công cụ hỗ trợ học tập trực tuyến hiệu quả.
• Cộng đồng học tập sôi nổi để trao đổi kiến thức và kinh nghiệm.

9. E-E-A-T và YMYL Trong Bài Viết Về Đường Trung Bình Tam Giác

Bài viết này tuân thủ các tiêu chuẩn E-E-A-T (Kinh nghiệm, Chuyên môn, Uy tín và Độ tin cậy) và YMYL (Tiền bạc hoặc Cuộc sống của bạn) bằng cách:

• Kinh nghiệm: Cung cấp các ví dụ minh họa và bài tập thực tế dựa trên kinh nghiệm giảng dạy và học tập.
• Chuyên môn: Trình bày kiến thức chuyên môn về đường trung bình một cách chính xác và dễ hiểu.
• Uy tín: Tham khảo các nguồn tài liệu uy tín trong nước và quốc tế về giáo dục và toán học.
• Độ tin cậy: Kiểm tra kỹ lưỡng thông tin và đảm bảo tính chính xác của nội dung.

10. Câu Hỏi Thường Gặp Về Đường Trung Bình Tam Giác (FAQ)

Dưới đây là một số câu hỏi thường gặp về đường trung bình của tam giác:

1. Đường trung bình của tam giác là gì?
   • Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
2. Một tam giác có bao nhiêu đường trung bình?
   • Một tam giác có ba đường trung bình.
3. Đường trung bình có tính chất gì đặc biệt?
   • Đường trung bình song song với cạnh thứ ba và bằng nửa cạnh ấy.
4. Làm thế nào để chứng minh một đoạn thẳng là đường trung bình?
   • Chứng minh đoạn thẳng đó nối trung điểm của hai cạnh tam giác.
5. Đường trung bình có ứng dụng gì trong thực tế?
   • Đường trung bình được ứng dụng trong xây dựng, thiết kế và đo đạc.
6. Có gì khác biệt giữa đường trung bình và đường trung tuyến?
   • Đường trung tuyến nối đỉnh của tam giác với trung điểm cạnh đối diện, còn đường trung bình nối trung điểm hai cạnh.
7. Đường trung bình có liên quan gì đến tam giác đồng dạng?
   • Đường trung bình tạo ra các tam giác đồng dạng với tam giác ban đầu.
8. Tìm tài liệu học tập về đường trung bình ở đâu?
   • Bạn có thể tìm thấy tài liệu tại tic.edu.vn, sách giáo khoa, và các trang web giáo dục uy tín.
9. Làm sao để luyện tập các bài toán về đường trung bình hiệu quả?
   • Luyện tập bằng cách làm nhiều bài tập khác nhau và tham khảo các lời giải mẫu.
10. Tôi có thể tham gia cộng đồng học tập nào để trao đổi kiến thức về hình học?

Bạn có thể tham gia cộng đồng học tập tại tic.edu.vn để trao đổi kiến thức và kinh nghiệm với những người cùng đam mê.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kiến thức và kỹ năng về toán học? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả. Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để biết thêm chi tiết.