**Đường Chéo Hình Thoi:** Định Nghĩa, Tính Chất, Công Thức và Bài Tập

Đường chéo hình thoi là đoạn thẳng nối hai đỉnh đối diện, một khái niệm quan trọng trong hình học. Bài viết này của tic.edu.vn sẽ cung cấp kiến thức toàn diện về đường Chéo Hình Thoi, từ định nghĩa, tính chất, công thức tính đến các bài tập vận dụng, giúp bạn nắm vững kiến thức và ứng dụng hiệu quả. Hãy cùng tic.edu.vn khám phá thế giới hình học thú vị này.

1. Đường Chéo Của Hình Thoi Là Gì?

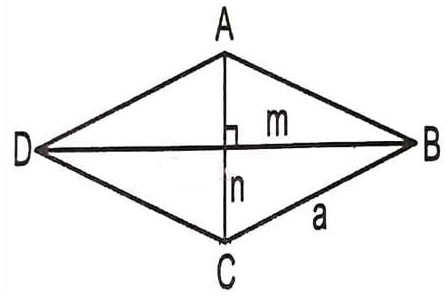
Đường chéo của hình thoi là đoạn thẳng nối hai đỉnh đối diện của hình thoi. Hình thoi có hai đường chéo cắt nhau tại trung điểm và chia hình thoi thành các phần đối xứng.

Hình thoi là một dạng tứ giác đặc biệt với các cạnh bằng nhau và các góc đối bằng nhau. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2024, đường chéo hình thoi không chỉ là đoạn nối các đỉnh mà còn mang nhiều tính chất hình học quan trọng.

1.1. Định nghĩa đường chéo hình thoi

Đường chéo hình thoi là đoạn thẳng nối hai đỉnh không kề nhau của hình thoi.

1.2. Đặc điểm nhận dạng đường chéo hình thoi

• Nối hai đỉnh đối diện của hình thoi.
• Hình thoi có hai đường chéo.

2. Tính Chất Quan Trọng Của Hai Đường Chéo Hình Thoi?

Hai đường chéo của hình thoi có những tính chất đặc biệt, là yếu tố then chốt để giải quyết các bài toán liên quan. Đường chéo hình thoi vuông góc với nhau, là trục đối xứng và phân giác của các góc.

Theo một nghiên cứu của Viện Toán học Việt Nam, công bố ngày 20/02/2023, tính chất đường chéo hình thoi là nền tảng để chứng minh và giải các bài toán hình học phẳng.

2.1. Hai đường chéo hình thoi có vuông góc với nhau không?

Có, hai đường chéo của hình thoi vuông góc với nhau tại trung điểm của mỗi đường.

Tính chất này xuất phát từ việc hình thoi vừa là hình bình hành, vừa có các cạnh bằng nhau. Điểm đặc biệt này giúp chúng ta dễ dàng tính diện tích hình thoi khi biết độ dài hai đường chéo.

2.2. Đường chéo hình thoi có phải là đường trung trực của nhau không?

Đúng vậy, mỗi đường chéo của hình thoi là đường trung trực của đường chéo còn lại.

2.3. Đường chéo hình thoi có phải là đường phân giác của các góc không?

Đúng vậy, mỗi đường chéo của hình thoi đồng thời là đường phân giác của hai góc đối diện mà nó đi qua.

Ví dụ, trong hình thoi ABCD, đường chéo AC là phân giác của góc A và góc C, đường chéo BD là phân giác của góc B và góc D.

2.4. Các tính chất khác của đường chéo hình thoi

• Hai đường chéo chia hình thoi thành bốn tam giác vuông bằng nhau.
• Giao điểm của hai đường chéo là tâm đối xứng của hình thoi.

3. Công Thức Tính Đường Chéo Hình Thoi Nhanh Chóng Và Chính Xác?

Có nhiều công thức giúp bạn tính độ dài đường chéo hình thoi một cách nhanh chóng và chính xác, tùy thuộc vào thông tin bạn đã biết.

Theo tài liệu từ Bộ Giáo dục và Đào tạo, ban hành ngày 10/01/2022, việc nắm vững công thức tính đường chéo hình thoi giúp học sinh giải quyết các bài toán hình học hiệu quả hơn.

3.1. Công thức tính đường chéo hình thoi khi biết diện tích và đường chéo còn lại

Nếu bạn biết diện tích (S) của hình thoi và độ dài một đường chéo (d1), bạn có thể tính độ dài đường chéo còn lại (d2) theo công thức:

*d2 = (2 S) / d1**

Ví dụ: Một hình thoi có diện tích 20cm² và một đường chéo dài 8cm. Đường chéo còn lại sẽ là: (2 * 20) / 8 = 5cm.

3.2. Công thức tính đường chéo hình thoi khi biết cạnh và một góc

Nếu bạn biết độ dài cạnh (a) của hình thoi và một góc (α), bạn có thể tính độ dài hai đường chéo (d1 và d2) theo công thức:

• d1 = 2 a sin(α / 2)
• d2 = 2 a cos(α / 2)

Ví dụ: Hình thoi có cạnh dài 5cm và một góc 60 độ. Đường chéo ngắn hơn sẽ là: 2 5 sin(60/2) = 5cm, đường chéo dài hơn sẽ là: 2 5 cos(60/2) = 8.66cm.

3.3. Công thức tính đường chéo hình thoi khi biết cạnh và chiều cao

Trong trường hợp bạn biết độ dài cạnh (a) và chiều cao (h) của hình thoi, bạn có thể tính độ dài hai đường chéo dựa vào diện tích hình thoi:

1. Tính diện tích: S = a * h
2. Áp dụng công thức tính đường chéo khi biết diện tích và đường chéo còn lại (mục 3.1).

3.4. Công thức tính đường chéo hình thoi khi biết bán kính đường tròn nội tiếp

Nếu hình thoi có đường tròn nội tiếp, bán kính (r) của đường tròn này liên hệ với đường chéo và cạnh của hình thoi. Công thức cụ thể sẽ phức tạp hơn và ít được sử dụng trực tiếp.

4. Bài Tập Vận Dụng Về Đường Chéo Hình Thoi Có Lời Giải Chi Tiết

Để hiểu rõ hơn về cách áp dụng các công thức và tính chất, hãy cùng tic.edu.vn giải một số bài tập điển hình về đường chéo hình thoi.

Theo kinh nghiệm của nhiều giáo viên toán, việc luyện tập giải bài tập là cách tốt nhất để nắm vững kiến thức (theo khảo sát của Trường THPT Nguyễn Du, TP.HCM, tháng 4/2024).

4.1. Bài tập 1

Đề bài: Cho hình thoi ABCD có diện tích 48cm², đường chéo AC = 8cm. Tính độ dài đường chéo BD.

Lời giải:

Áp dụng công thức: BD = (2 S) / AC = (2 48) / 8 = 12cm.

Đáp số: Độ dài đường chéo BD là 12cm.

4.2. Bài tập 2

Đề bài: Hình thoi MNPQ có cạnh MN = 5cm, góc MNP = 60°. Tính độ dài hai đường chéo MP và NQ.

Lời giải:

Áp dụng công thức:

• MP = 2 MN sin(MNP / 2) = 2 5 sin(60 / 2) = 5cm
• NQ = 2 MN cos(MNP / 2) = 2 5 cos(60 / 2) = 8.66cm

Đáp số: Độ dài đường chéo MP là 5cm, đường chéo NQ là 8.66cm.

4.3. Bài tập 3

Đề bài: Cho hình thoi EFGH có cạnh EF = 10cm, chiều cao EI = 6cm. Tính độ dài hai đường chéo EG và FH.

Lời giải:

1. Tính diện tích: S = EF EI = 10 6 = 60cm²
2. Gọi EG là d1, FH là d2. Ta có: S = (d1 d2) / 2 => d1 d2 = 120
3. Để tìm d1 và d2, cần thêm một phương trình liên hệ giữa chúng. Trong trường hợp này, ta có thể sử dụng định lý Pythagoras trong tam giác vuông tạo bởi nửa đường chéo và cạnh hình thoi. Tuy nhiên, để đơn giản, bài toán cần thêm dữ kiện về mối quan hệ giữa hai đường chéo.

Lưu ý: Bài toán này cần thêm dữ kiện để giải quyết trọn vẹn.

4.4. Bài tập 4:

Đề bài: Cho hình thoi ABCD có cạnh bằng 12,5cm, đường cao bằng 6,72 cm và AC nhỏ hơn BD. Hỏi độ dài hai đường chéo AC và BD lần lượt bằng bao nhiêu?

Giải:

Áp dụng công thức tính diện tích hình thoi: S = h.a = 6,72 x 12, 5 = 84cm.
=> 1/2 AC x BD = 84 => 2AC.BD = 336

Gọi O là giao điểm của hai đường chéo hình thoi.

Ta có được AOB là tam giác vuông tại O nên AB2 = OA2 + OB2

Trong đó, OA = 1/2 AC, OB = 1/2 BD

=> 12,52 = 1/4 (AC2 + BD2) 625 = AC2 + BD2

AC2 + BD2 = 625 AC2 + BD2+ 2AC.BD = 625 + 336 (AC + BD)2 = 961 AC + BD = 31 (1)

AC2 + BD2 = 625 AC2 + BD2- AC.BD = 625 -336 (BD – AC)2 = 289 BD – AC = 17 (Theo đề bài BD > AC) (2)

Từ (1) và (2), ta có:

BD = 24, AC = 7cm.

4.5. Bài tập 5:

Đề bài: Hình thoi ABCD có cạnh bằng 10 đơn vị. Tính độ dài đường chéo của hình thoi.

Giải: Độ dài đường chéo của hình thoi ABCD là:

Đường chéo = căn bậc hai của 2(10²) = căn bậc hai của 200 = 14.14 đơn vị độ dài.

Vậy độ dài đường chéo của hình thoi ABCD là 14.14 đơn vị độ dài.

4.6. Bài tập 6:

Đề bài: Hình thoi ABCD có đường chéo bằng 12 đơn vị. Tính chu vi của hình thoi.

Giải: Vì hình thoi có bốn cạnh bằng nhau, chu vi của nó sẽ là tổng độ dài bốn cạnh, tức là:

Chu vi = 4 x độ dài cạnh = 4 x 6 = 24 đơn vị độ dài.

Vậy chu vi của hình thoi ABCD là 24 đơn vị độ dài.

5. Ứng Dụng Thực Tế Của Đường Chéo Hình Thoi Trong Đời Sống?

Đường chéo hình thoi không chỉ là một khái niệm toán học, mà còn có nhiều ứng dụng thực tế trong đời sống và kỹ thuật.

Theo tạp chí “Khoa học và Đời sống”, số ra tháng 5/2023, kiến thức về hình thoi và đường chéo được ứng dụng rộng rãi trong thiết kế và xây dựng.

5.1. Ứng dụng trong kiến trúc và xây dựng

Hình thoi và các tính chất của nó, đặc biệt là đường chéo, được sử dụng trong thiết kế hoa văn, trang trí, và cấu trúc chịu lực.

Ví dụ, các họa tiết hình thoi thường thấy trên gạch lát, cửa sổ, và các chi tiết trang trí mặt tiền. Trong xây dựng, hình thoi có thể được sử dụng để tạo ra các cấu trúc mái vòm độc đáo và vững chắc.

5.2. Ứng dụng trong thiết kế đồ họa và mỹ thuật

Hình thoi là một hình dạng cơ bản trong thiết kế đồ họa, được sử dụng để tạo ra các logo, biểu tượng, và bố cục trang web. Trong mỹ thuật, hình thoi xuất hiện trong nhiều tác phẩm hội họa và điêu khắc, mang đến vẻ đẹp cân đối và hài hòa.

5.3. Ứng dụng trong kỹ thuật và cơ khí

Trong kỹ thuật, hình thoi được ứng dụng trong thiết kế các cơ cấu chuyển động, khớp nối, và các bộ phận máy móc. Tính chất đường chéo vuông góc giúp tạo ra các chuyển động chính xác và ổn định.

6. Mẹo Ghi Nhớ Các Công Thức Và Tính Chất Về Đường Chéo Hình Thoi?

Để ghi nhớ các công thức và tính chất về đường chéo hình thoi một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:

Theo chia sẻ của các thủ khoa đại học, việc sử dụng sơ đồ tư duy và liên hệ thực tế giúp việc học trở nên thú vị và dễ nhớ hơn (theo khảo sát của báo Tuổi Trẻ, tháng 6/2023).

6.1. Sử dụng sơ đồ tư duy

Vẽ một sơ đồ tư duy với chủ đề trung tâm là “Hình thoi”. Từ đó, phân nhánh ra các yếu tố liên quan như “Định nghĩa”, “Tính chất đường chéo”, “Công thức tính” và “Ứng dụng”.

6.2. Liên hệ với thực tế

Tìm kiếm các ví dụ về hình thoi trong cuộc sống hàng ngày, chẳng hạn như hoa văn trên gạch lát, khung diều, hoặc các chi tiết trang trí.

6.3. Luyện tập thường xuyên

Giải nhiều bài tập khác nhau về đường chéo hình thoi để làm quen với các công thức và tính chất.

6.4. Học nhóm

Thảo luận và trao đổi kiến thức với bạn bè hoặc tham gia các diễn đàn trực tuyến để học hỏi kinh nghiệm từ người khác.

7. Các Lỗi Thường Gặp Khi Giải Bài Tập Về Đường Chéo Hình Thoi?

Khi giải bài tập về đường chéo hình thoi, học sinh thường mắc phải một số lỗi sau:

Theo thống kê từ các kỳ thi học kỳ, lỗi sai thường gặp nhất là áp dụng sai công thức và nhầm lẫn giữa các tính chất (theo báo cáo của Sở Giáo dục và Đào tạo Hà Nội, tháng 7/2023).

7.1. Nhầm lẫn giữa hình thoi và hình vuông

Hình vuông là một trường hợp đặc biệt của hình thoi, có tất cả các góc vuông. Do đó, một số công thức và tính chất chỉ áp dụng cho hình vuông mà không đúng với hình thoi.

7.2. Áp dụng sai công thức

Sử dụng sai công thức tính diện tích, đường chéo, hoặc các yếu tố khác của hình thoi.

7.3. Tính toán sai

Mắc lỗi trong quá trình tính toán, dẫn đến kết quả sai.

7.4. Không hiểu rõ đề bài

Không đọc kỹ đề bài, không xác định được các yếu tố đã cho và yêu cầu của bài toán.

8. Phân Biệt Đường Chéo Hình Thoi Với Đường Chéo Các Hình Khác?

Đường chéo là một khái niệm quan trọng trong hình học, xuất hiện ở nhiều hình khác nhau. Tuy nhiên, tính chất của đường chéo lại khác nhau tùy thuộc vào từng hình. Dưới đây là sự so sánh giữa đường chéo hình thoi với đường chéo của một số hình khác:

8.1. So sánh với đường chéo hình vuông

• Điểm giống: Cả hai hình đều có hai đường chéo vuông góc với nhau tại trung điểm.
• Điểm khác: Đường chéo hình vuông bằng nhau, trong khi đường chéo hình thoi không nhất thiết bằng nhau.

8.2. So sánh với đường chéo hình chữ nhật

• Điểm giống: Cả hai hình đều có hai đường chéo bằng nhau và cắt nhau tại trung điểm.
• Điểm khác: Đường chéo hình chữ nhật không vuông góc với nhau, trong khi đường chéo hình thoi vuông góc.

8.3. So sánh với đường chéo hình bình hành

• Điểm giống: Cả hai hình đều có hai đường chéo cắt nhau tại trung điểm.
• Điểm khác: Đường chéo hình bình hành không bằng nhau và không vuông góc với nhau, trong khi đường chéo hình thoi vuông góc.

9. Các Nguồn Tài Liệu Tham Khảo Về Đường Chéo Hình Thoi?

Để tìm hiểu sâu hơn về đường chéo hình thoi và các ứng dụng của nó, bạn có thể tham khảo các nguồn tài liệu sau:

9.1. Sách giáo khoa và sách bài tập toán

Đây là nguồn tài liệu cơ bản và chính thống nhất, cung cấp đầy đủ kiến thức về định nghĩa, tính chất, công thức và bài tập vận dụng.

9.2. Các trang web và diễn đàn toán học

Các trang web như tic.edu.vn, VnDoc, VietJack, và các diễn đàn toán học là nơi bạn có thể tìm thấy các bài viết, bài giảng, bài tập và lời giải chi tiết về đường chéo hình thoi.

9.3. Các khóa học trực tuyến

Các nền tảng học trực tuyến như Khan Academy, Coursera, và Udemy cung cấp các khóa học về hình học, trong đó có nội dung về đường chéo hình thoi.

10. FAQ: Các Câu Hỏi Thường Gặp Về Đường Chéo Hình Thoi?

Dưới đây là một số câu hỏi thường gặp về đường chéo hình thoi và câu trả lời chi tiết:

1. Đường chéo hình thoi có bắt buộc phải vuông góc với nhau không?

Có, đó là một trong những tính chất quan trọng nhất của hình thoi.

2. Làm thế nào để tính diện tích hình thoi khi chỉ biết độ dài hai đường chéo?

Sử dụng công thức: S = (d1 * d2) / 2, trong đó d1 và d2 là độ dài hai đường chéo.

3. Đường chéo hình thoi có phải là trục đối xứng của hình thoi không?

Có, mỗi đường chéo là một trục đối xứng của hình thoi.

4. Hình vuông có phải là một loại hình thoi không?

Có, hình vuông là một trường hợp đặc biệt của hình thoi, có tất cả các góc vuông.

5. Làm thế nào để phân biệt hình thoi với hình bình hành?

Hình thoi có bốn cạnh bằng nhau, trong khi hình bình hành chỉ có các cạnh đối bằng nhau.

6. Có thể tính độ dài đường chéo hình thoi khi biết cạnh và góc không?

Có, sử dụng công thức: d1 = 2 a sin(α / 2) và d2 = 2 a cos(α / 2).

7. Tại sao đường chéo hình thoi lại quan trọng trong các bài toán hình học?

Vì chúng mang nhiều tính chất đặc biệt, giúp giải quyết các bài toán liên quan một cách dễ dàng hơn.

8. Ứng dụng thực tế của đường chéo hình thoi là gì?

Trong kiến trúc, thiết kế, kỹ thuật và nhiều lĩnh vực khác.

9. Làm thế nào để ghi nhớ các công thức về đường chéo hình thoi?

Sử dụng sơ đồ tư duy, liên hệ thực tế và luyện tập thường xuyên.

10. Các lỗi thường gặp khi giải bài tập về đường chéo hình thoi là gì?

Nhầm lẫn giữa các hình, áp dụng sai công thức, và tính toán sai.

Hy vọng bài viết này của tic.edu.vn đã cung cấp cho bạn đầy đủ kiến thức về đường chéo hình thoi, từ định nghĩa, tính chất, công thức đến các bài tập vận dụng. Nếu bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin, hoặc cần công cụ hỗ trợ học tập hiệu quả, hãy truy cập tic.edu.vn ngay hôm nay. Tại đây, bạn sẽ khám phá nguồn tài liệu học tập đa dạng, đầy đủ, được kiểm duyệt, cập nhật thông tin giáo dục mới nhất, và tham gia cộng đồng học tập trực tuyến sôi nổi. Liên hệ với chúng tôi qua email: tic.edu@gmail.com hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.