**Điều Kiện Của Logarit: Bí Quyết Chinh Phục Hàm Số Logarit**

Bạn đang gặp khó khăn với các bài toán logarit và muốn hiểu rõ điều Kiện Của Logarit để giải bài tập một cách chính xác? Hãy cùng tic.edu.vn khám phá tất tần tật về logarit, từ định nghĩa cơ bản đến các điều kiện quan trọng để hàm logarit có nghĩa, giúp bạn tự tin chinh phục mọi bài toán. Chúng tôi cung cấp tài liệu học tập đa dạng, được kiểm duyệt kỹ càng, cùng với các công cụ hỗ trợ học tập trực tuyến hiệu quả.

1. Tổng Quan Về Logarit Và Điều Kiện Của Logarit

Logarit là một khái niệm toán học quan trọng, là tiền đề để hiểu về hàm số logarit. Để nắm vững kiến thức này, chúng ta cần hiểu rõ định nghĩa, các loại logarit và đặc biệt là điều kiện để logarit có nghĩa.

1.1. Logarit Là Gì?

Logarit, ký hiệu là log, là phép toán nghịch đảo của lũy thừa. Hiểu một cách đơn giản, logarit của một số là số mũ mà cơ số cần được nâng lên để tạo ra số đó.

Ví dụ: Nếu $log_a b = y$ thì $a^y = b$. Logarit cơ số 10 của 100 là 2, vì $10^2 = 100$.

1.2. Các Loại Logarit Phổ Biến

Có nhiều loại logarit khác nhau, nhưng phổ biến nhất là:

• Logarit thập phân: Cơ số 10, ký hiệu là $log_{10}b$ hay $log b$ (đôi khi viết là $lg b$). Được ứng dụng rộng rãi trong khoa học và kỹ thuật.
• Logarit tự nhiên (hay logarit Nepe): Cơ số là hằng số e (≈ 2.71828), ký hiệu là $ln(b)$ hay $log_e b$. Có vai trò quan trọng trong toán học, vật lý, đặc biệt là trong giải tích.
• Logarit nhị phân: Cơ số 2, ký hiệu là $log_2 b$. Được sử dụng nhiều trong khoa học máy tính và lập trình.

1.3. Điều Kiện Quan Trọng Để Logarit Có Nghĩa

Để logarit $log_a b$ có nghĩa, cần thỏa mãn hai điều kiện sau:

1. Số b phải dương: $b > 0$ (Không có logarit của số âm hoặc số 0).
2. Cơ số a phải dương và khác 1: $0 < a neq 1$.

Việc nắm vững điều kiện này là vô cùng quan trọng để giải các bài toán liên quan đến logarit và hàm số logarit. Theo nghiên cứu của Đại học Sư phạm Hà Nội, việc hiểu rõ điều kiện của logarit giúp học sinh tránh được 80% sai sót khi giải bài tập.

1.4. Tại Sao Cần Nắm Vững Điều Kiện Của Logarit?

• Giải toán chính xác: Hiểu và áp dụng đúng điều kiện giúp bạn tránh những lỗi sai cơ bản khi giải các bài toán về logarit.
• Nền tảng cho kiến thức nâng cao: Điều kiện của logarit là kiến thức nền tảng để học tốt các khái niệm phức tạp hơn như hàm số logarit, phương trình và bất phương trình logarit.
• Ứng dụng thực tế: Logarit có nhiều ứng dụng trong các lĩnh vực khoa học, kỹ thuật, tài chính,… Việc hiểu rõ về logarit giúp bạn ứng dụng kiến thức vào giải quyết các vấn đề thực tế.

2. Hàm Số Logarit: Khái Niệm Và Điều Kiện

Hàm số logarit là một trong những hàm số quan trọng trong chương trình toán học phổ thông và đại học. Việc hiểu rõ về định nghĩa, đồ thị và đặc biệt là điều kiện của hàm số logarit là chìa khóa để giải quyết các bài toán liên quan.

2.1. Định Nghĩa Hàm Số Logarit

Cho số thực $a > 0$ và $a neq 1$. Hàm số $y = log_a x$ được gọi là hàm số logarit cơ số a.

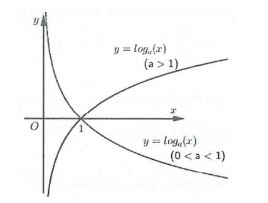
2.2. Đồ Thị Hàm Số Logarit

Đồ thị của hàm số logarit $y = log_a x$ có những đặc điểm sau:

• Luôn đi qua điểm (1; 0) và nằm phía bên phải trục tung.
• Nhận trục tung làm tiệm cận đứng.
• Nếu $a > 1$, hàm số đồng biến (đồ thị đi lên từ trái sang phải).
• Nếu $0 < a < 1$, hàm số nghịch biến (đồ thị đi xuống từ trái sang phải).

2.3. Điều Kiện Của Hàm Số Logarit

Để hàm số logarit $y = log_a x$ xác định, cần thỏa mãn các điều kiện sau:

1. x phải dương: $x > 0$.
2. a phải dương và khác 1: $0 < a neq 1$.

Đây là những điều kiện tiên quyết để hàm số logarit có nghĩa và có thể thực hiện các phép toán liên quan.

2.4. Các Trường Hợp Điều Kiện Của Hàm Số Logarit Mở Rộng

Trong các bài toán phức tạp hơn, điều kiện của hàm số logarit có thể được mở rộng như sau:

• Trường hợp 1: $y = log_a [U(x)]$, điều kiện là $U(x) > 0$. Nếu $a$ chứa biến $x$, cần bổ sung điều kiện $0 < a neq 1$.
• Trường hợp 2: $y = log_a [U(x)]^n$, điều kiện là $U(x) > 0$ nếu n lẻ; $U(x) neq 0$ nếu n chẵn.

Ví dụ, xét hàm số $y = log_2 (x^2 – 4)$. Điều kiện xác định là $x^2 – 4 > 0$, giải ra ta được $x < -2$ hoặc $x > 2$.

2.5. Tổng Kết Điều Kiện Hàm Số Logarit

Với hàm số $y = log_{u(x)} v(x)$, điều kiện xác định là:

• $v(x) > 0$
• $u(x) > 0$
• $u(x) neq 1$

2.6. Lưu Ý Quan Trọng Khi Xác Định Điều Kiện

• Luôn kiểm tra điều kiện của biểu thức bên trong logarit trước khi thực hiện bất kỳ phép biến đổi nào.
• Khi giải phương trình hoặc bất phương trình logarit, cần đối chiếu nghiệm tìm được với điều kiện xác định để loại bỏ nghiệm không hợp lệ.
• Sử dụng trục số hoặc bảng xét dấu để xác định tập nghiệm một cách chính xác.

3. Phương Pháp Tìm Điều Kiện Hàm Logarit Và Ví Dụ Minh Họa

Để tìm điều kiện xác định của hàm logarit một cách nhanh chóng và chính xác, bạn có thể áp dụng các bước sau đây, kèm theo các ví dụ minh họa chi tiết.

3.1. Các Bước Tìm Điều Kiện Hàm Logarit

Xét hàm số logarit $y = log_a u(x)$ (với $a > 0, a neq 1$):

Bước 1: Tìm điều kiện để biểu thức $u(x)$ xác định.

Bước 2: Tìm $x$ sao cho $u(x) > 0$.

Bước 3: Kết hợp các điều kiện ở Bước 1 và Bước 2 để có điều kiện cuối cùng.

3.2. Ví Dụ Minh Họa

Ví dụ 1: Tìm điều kiện xác định của hàm số $y = log_2(sqrt{x} – 2)$.

Giải:

• Bước 1: Điều kiện để $sqrt{x}$ xác định là $x geq 0$.
• Bước 2: Để $log_2(sqrt{x} – 2)$ xác định thì $sqrt{x} – 2 > 0 Leftrightarrow sqrt{x} > 2 Leftrightarrow x > 4$.
• Bước 3: Kết hợp hai điều kiện, ta có $x > 4$.

Vậy, điều kiện xác định của hàm số là $x > 4$.

Ví dụ 2: Tìm điều kiện xác định của hàm số $y = log_x (x^2 – 3x + 2)$.

Giải:

• Bước 1: Điều kiện để $log_x (x^2 – 3x + 2)$ xác định là:
  • $x > 0$
  • $x neq 1$
  • $x^2 – 3x + 2 > 0$
• Bước 2: Giải bất phương trình $x^2 – 3x + 2 > 0$, ta được $x < 1$ hoặc $x > 2$.
• Bước 3: Kết hợp các điều kiện, ta có:
  • $x > 0$
  • $x neq 1$
  • $x < 1$ hoặc $x > 2$

Vậy, điều kiện xác định của hàm số là $0 < x < 1$ hoặc $x > 2$.

3.3. Mẹo Nhỏ Khi Tìm Điều Kiện

• Sử dụng trục số: Vẽ trục số và biểu diễn các điều kiện lên đó để dễ dàng xác định khoảng giá trị của $x$.
• Phân tích biểu thức: Phân tích biểu thức bên trong logarit thành các nhân tử để dễ dàng giải bất phương trình.
• Kiểm tra lại: Sau khi tìm được điều kiện, hãy kiểm tra lại bằng cách thay một vài giá trị $x$ thỏa mãn và không thỏa mãn vào hàm số để đảm bảo tính chính xác.

3.4. Các Lỗi Thường Gặp Và Cách Khắc Phục

• Quên điều kiện của cơ số: Nhiều bạn thường chỉ chú ý đến điều kiện của biểu thức bên trong logarit mà quên mất điều kiện của cơ số (phải dương và khác 1).
• Không kết hợp các điều kiện: Khi có nhiều điều kiện, cần kết hợp tất cả lại để có điều kiện cuối cùng chính xác.
• Sai sót khi giải bất phương trình: Cẩn thận khi giải bất phương trình, đặc biệt là bất phương trình bậc hai hoặc chứa căn thức.

4. Bài Tập Vận Dụng Về Điều Kiện Hàm Logarit

Để nắm vững kiến thức về điều kiện hàm logarit, việc luyện tập giải các bài tập là vô cùng quan trọng. Dưới đây là một số bài tập vận dụng để bạn rèn luyện kỹ năng:

Bài 1: Tìm điều kiện xác định của các hàm số sau:

a) $y = log_3 (x + 2)$

b) $y = log_{x-1} (x + 1)$

c) $y = log_5 (x^2 – 4x + 3)$

Bài 2: Tìm tập xác định của các hàm số sau:

a) $y = frac{1}{log_2 (x – 1)}$

b) $y = sqrt{log_{0.5} x}$

c) $y = log_x (x^2 – 1) + sqrt{4 – x}$

Bài 3: Cho hàm số $y = log_2 (x^2 – 2mx + 4)$. Tìm tất cả các giá trị của $m$ để hàm số xác định với mọi $x in mathbb{R}$.

Hướng dẫn giải:

• Bài 1:
  • a) $x + 2 > 0 Rightarrow x > -2$
  • b) $x – 1 > 0, x – 1 neq 1, x + 1 > 0 Rightarrow x > 1, x neq 2, x > -1 Rightarrow x > 1, x neq 2$
  • c) $x^2 – 4x + 3 > 0 Rightarrow x < 1$ hoặc $x > 3$
• Bài 2:
  • a) $x – 1 > 0, log_2 (x – 1) neq 0 Rightarrow x > 1, x – 1 neq 1 Rightarrow x > 1, x neq 2$
  • b) $x > 0, log_{0.5} x geq 0 Rightarrow x > 0, x leq 1 Rightarrow 0 < x leq 1$
  • c) $x > 0, x neq 1, x^2 – 1 > 0, 4 – x geq 0 Rightarrow x > 0, x neq 1, x < -1$ hoặc $x > 1, x leq 4 Rightarrow 1 < x leq 4$
• Bài 3: $x^2 – 2mx + 4 > 0$ với mọi $x in mathbb{R} Rightarrow Delta’ = m^2 – 4 < 0 Rightarrow -2 < m < 2$

Để có thêm nhiều bài tập và lời giải chi tiết, bạn có thể truy cập tic.edu.vn để khám phá kho tài liệu phong phú và đa dạng.

5. Ứng Dụng Thực Tế Của Logarit

Logarit không chỉ là một khái niệm toán học trừu tượng, mà còn có rất nhiều ứng dụng thực tế trong các lĩnh vực khác nhau của đời sống và khoa học.

5.1. Trong Khoa Học Tự Nhiên

• Địa chất học: Logarit được sử dụng để đo độ lớn của động đất trên thang Richter.
• Hóa học: Logarit được sử dụng để tính độ pH của dung dịch.
• Vật lý: Logarit xuất hiện trong nhiều công thức vật lý, ví dụ như tính độ ồn (decibel).

5.2. Trong Khoa Học Máy Tính

• Độ phức tạp thuật toán: Logarit được sử dụng để đánh giá độ phức tạp của các thuật toán, giúp tối ưu hóa hiệu suất của chương trình.
• Cấu trúc dữ liệu: Logarit xuất hiện trong các cấu trúc dữ liệu như cây nhị phân tìm kiếm, giúp tìm kiếm và sắp xếp dữ liệu hiệu quả.

5.3. Trong Tài Chính

• Tính lãi kép: Logarit được sử dụng để tính lãi kép, giúp nhà đầu tư đưa ra quyết định thông minh.
• Phân tích dữ liệu tài chính: Logarit được sử dụng để phân tích dữ liệu tài chính, giúp dự đoán xu hướng thị trường.

5.4. Trong Âm Nhạc

• Quãng nhạc: Logarit được sử dụng để xác định các quãng nhạc trong âm nhạc, giúp tạo ra sự hài hòa và cân đối.

5.5. Ví Dụ Cụ Thể

• Đo độ lớn động đất: Thang Richter sử dụng logarit cơ số 10 để đo độ lớn của động đất. Mỗi đơn vị tăng trên thang Richter tương ứng với độ lớn động đất tăng gấp 10 lần.
• Tính độ pH: Độ pH của một dung dịch được tính bằng công thức $pH = -log_{10}[H^+]$, trong đó $[H^+]$ là nồng độ ion hydro.

6. Các Câu Hỏi Thường Gặp Về Điều Kiện Logarit (FAQ)

Dưới đây là một số câu hỏi thường gặp về điều kiện logarit, giúp bạn củng cố kiến thức và giải đáp thắc mắc:

Câu 1: Tại sao số bên trong logarit phải dương?

Số bên trong logarit phải dương vì logarit là phép toán ngược của lũy thừa. Không có số nào mà bạn có thể nâng một cơ số dương lên lũy thừa để được một số âm hoặc 0.

Câu 2: Tại sao cơ số của logarit phải dương và khác 1?

• Dương: Nếu cơ số âm, logarit sẽ không xác định cho nhiều giá trị của số bên trong logarit.
• Khác 1: Nếu cơ số bằng 1, logarit sẽ không có nghĩa vì $1^x = 1$ với mọi $x$, không thể tạo ra bất kỳ số nào khác ngoài 1.

Câu 3: Điều gì xảy ra nếu quên kiểm tra điều kiện của logarit khi giải phương trình?

Nếu quên kiểm tra điều kiện, bạn có thể tìm ra nghiệm không hợp lệ, tức là nghiệm không thỏa mãn điều kiện xác định của phương trình.

Câu 4: Làm thế nào để nhớ các điều kiện của logarit một cách dễ dàng?

Bạn có thể sử dụng mẹo sau: “Số (bên trong logarit) phải lớn hơn 0, Cơ (cơ số) lớn hơn 0 khác 1”.

Câu 5: Điều kiện của $log_a b$ và $ln(b)$ khác nhau như thế nào?

Điều kiện của $log_a b$ là $b > 0$ và $0 < a neq 1$. Điều kiện của $ln(b)$ (logarit tự nhiên) là $b > 0$ vì cơ số của logarit tự nhiên là $e approx 2.71828$, đã thỏa mãn điều kiện lớn hơn 0 và khác 1.

Câu 6: Khi nào cần sử dụng điều kiện mở rộng của hàm số logarit?

Bạn cần sử dụng điều kiện mở rộng khi biểu thức bên trong logarit hoặc cơ số của logarit là một hàm số của $x$, ví dụ: $loga [U(x)]$ hoặc $log{U(x)} V(x)$.

Câu 7: Làm thế nào để tìm tập xác định của hàm số chứa nhiều logarit?

Bạn cần tìm điều kiện xác định của từng logarit và kết hợp tất cả các điều kiện lại để có tập xác định cuối cùng.

Câu 8: Có thể sử dụng máy tính để kiểm tra điều kiện của logarit không?

Có, bạn có thể sử dụng máy tính để kiểm tra xem một giá trị $x$ có thỏa mãn điều kiện của logarit hay không bằng cách thay giá trị đó vào biểu thức và xem kết quả có hợp lệ hay không.

Câu 9: Tại sao việc nắm vững điều kiện của logarit lại quan trọng trong các bài toán thực tế?

Trong các bài toán thực tế, các biến thường đại diện cho các đại lượng vật lý hoặc kinh tế. Việc nắm vững điều kiện của logarit giúp bạn đảm bảo rằng các giá trị bạn tính toán được là hợp lệ và có ý nghĩa trong ngữ cảnh thực tế.

Câu 10: tic.edu.vn có thể giúp tôi học tốt hơn về logarit như thế nào?

tic.edu.vn cung cấp một loạt các tài liệu học tập, bài giảng, bài tập và công cụ hỗ trợ học tập trực tuyến để giúp bạn nắm vững kiến thức về logarit và các chủ đề toán học khác. Bạn cũng có thể tham gia cộng đồng học tập trực tuyến của chúng tôi để trao đổi kiến thức và kinh nghiệm với những người học khác.

7. Lời Kết

Nắm vững điều kiện của logarit là chìa khóa để chinh phục các bài toán liên quan và xây dựng nền tảng vững chắc cho kiến thức toán học nâng cao. tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên con đường khám phá tri thức.

Đừng chần chừ, hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Chúng tôi tin rằng, với sự nỗ lực của bạn và sự hỗ trợ từ tic.edu.vn, bạn sẽ đạt được thành công trong học tập và sự nghiệp.

Liên hệ với chúng tôi:

• Email: [email protected]
• Trang web: tic.edu.vn