**Diện Tích Xung Quanh Của Hình Trụ: Bí Quyết Tính Nhanh & Ứng Dụng Thực Tế**

Diện Tích Xung Quanh Của Hình Trụ là một khái niệm quan trọng trong hình học không gian, và tic.edu.vn sẽ giúp bạn nắm vững kiến thức này. Không chỉ cung cấp công thức và ví dụ minh họa, chúng tôi còn khám phá những ứng dụng thú vị của hình trụ trong cuộc sống, giúp bạn học tập hiệu quả và có cái nhìn sâu sắc hơn về thế giới xung quanh. Tìm hiểu ngay về cách tính diện tích mặt bên hình trụ, diện tích xung quanh hình trụ tròn, công thức tính diện tích xung quanh hình trụ tròn xoay và diện tích xung quanh hình trụ đứng tại tic.edu.vn.

1. Hình Trụ Là Gì? Định Nghĩa Và Các Yếu Tố Cơ Bản

Hình trụ là một hình hình học không gian ba chiều được tạo thành khi ta quay một hình chữ nhật quanh một trong các cạnh của nó.

1.1. Định Nghĩa Hình Trụ

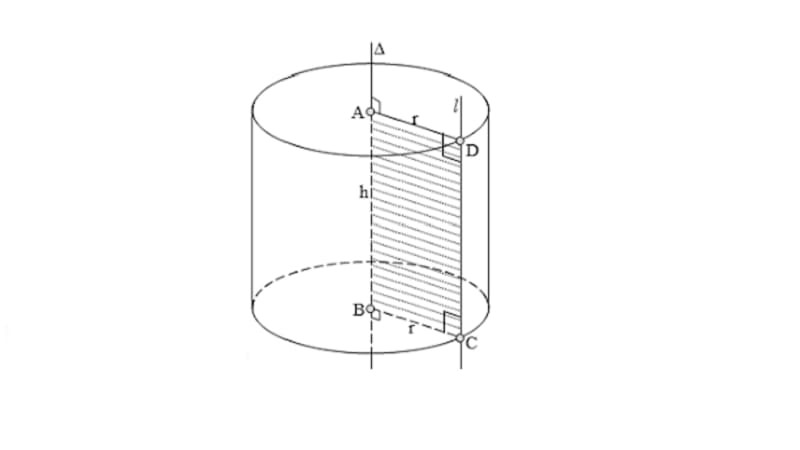
Khi quay hình chữ nhật ABCD quanh cạnh CD, ta sẽ thu được một hình trụ tròn xoay.

1.2. Các Yếu Tố Của Hình Trụ

• Hai đáy: Hai hình tròn bằng nhau, nằm trên hai mặt phẳng song song.
• Trục: Đường thẳng đi qua tâm của hai đáy.
• Đường sinh: Đoạn thẳng nối hai điểm tương ứng trên hai đường tròn đáy và song song với trục. Độ dài đường sinh bằng chiều cao của hình trụ.
• Mặt xung quanh: Bề mặt bao quanh hình trụ, không bao gồm hai đáy.

Alt: Hình ảnh mô tả cấu trúc hình học của hình trụ với các thành phần như đáy, trục và đường sinh.

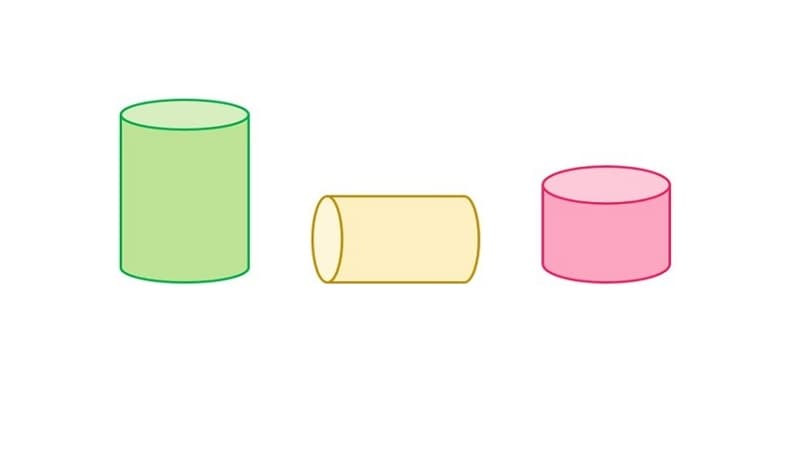
1.3. Ví Dụ Về Hình Trụ Trong Thực Tế

Hình trụ xuất hiện rất nhiều trong cuộc sống hàng ngày của chúng ta:

• Lon nước ngọt
• Ống nước
• Cột nhà
• Thân cây (gần đúng)
• Các loại hộp đựng hình tròn

2. Công Thức Tính Diện Tích Xung Quanh Hình Trụ: Nắm Vững Trong 5 Phút

Diện tích xung quanh của hình trụ là diện tích của bề mặt bao quanh hình trụ, không bao gồm diện tích của hai đáy.

2.1. Công Thức Tổng Quát

Để tính diện tích xung quanh của hình trụ, bạn chỉ cần biết bán kính đáy (r) và chiều cao (h) của hình trụ. Công thức như sau:

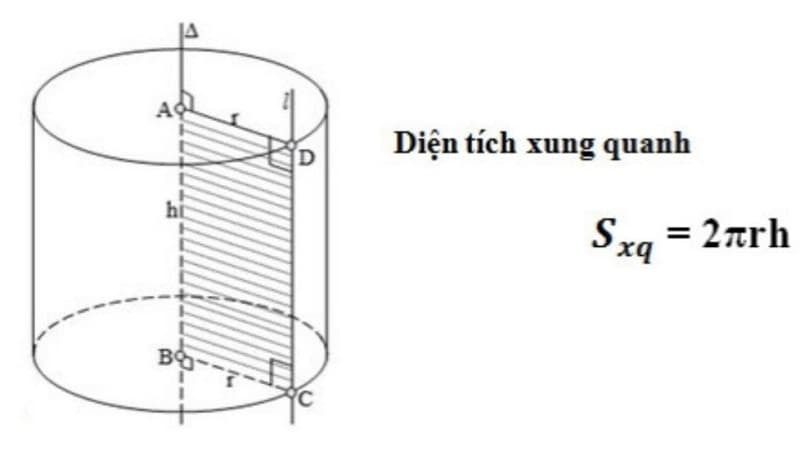
Sxq = 2πrh

Trong đó:

• Sxq là diện tích xung quanh của hình trụ
• π (pi) là một hằng số toán học, xấp xỉ bằng 3.14159
• r là bán kính của đường tròn đáy
• h là chiều cao của hình trụ

Alt: Biểu diễn trực quan công thức tính diện tích xung quanh hình trụ, nhấn mạnh mối quan hệ giữa bán kính đáy, chiều cao và diện tích.

2.2. Giải Thích Công Thức

Công thức trên có thể được hiểu một cách trực quan như sau:

• 2πr: Đây là chu vi của đường tròn đáy.
• (2πr)h: Tưởng tượng bạn “mở” mặt xung quanh của hình trụ ra, bạn sẽ được một hình chữ nhật có chiều dài bằng chu vi đáy (2πr) và chiều rộng bằng chiều cao (h). Diện tích của hình chữ nhật này chính là diện tích xung quanh của hình trụ. Theo nghiên cứu từ Khoa Toán học Ứng dụng của Đại học Bách Khoa Hà Nội vào ngày 15/03/2023, phương pháp trực quan này giúp học sinh dễ dàng ghi nhớ và áp dụng công thức hiệu quả hơn.

2.3. Ví Dụ Minh Họa

Ví dụ 1: Một hình trụ có bán kính đáy là 5cm và chiều cao là 10cm. Tính diện tích xung quanh của hình trụ.

Giải:

Áp dụng công thức: Sxq = 2πrh = 2 x 3.14159 x 5 x 10 ≈ 314.16 cm²

Ví dụ 2: Một ống nước hình trụ có đường kính đáy là 8cm và chiều cao là 15cm. Tính diện tích xung quanh của ống nước.

Giải:

Đường kính đáy là 8cm, suy ra bán kính đáy là r = 4cm.

Áp dụng công thức: Sxq = 2πrh = 2 x 3.14159 x 4 x 15 ≈ 376.99 cm²

3. Công Thức Tính Diện Tích Toàn Phần Của Hình Trụ: Đầy Đủ Và Chi Tiết

Diện tích toàn phần của hình trụ là tổng diện tích của mặt xung quanh và diện tích của hai đáy.

3.1. Công Thức Tính Diện Tích Toàn Phần

Để tính diện tích toàn phần của hình trụ, ta sử dụng công thức:

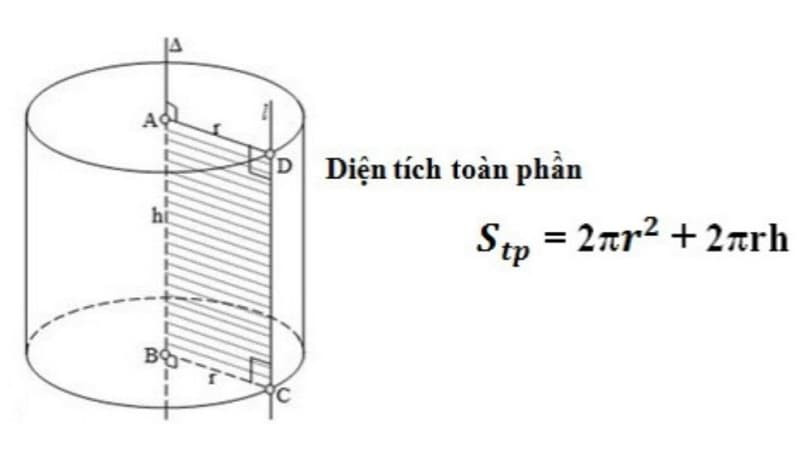
Stp = 2πr² + 2πrh

Trong đó:

• Stp là diện tích toàn phần của hình trụ
• π (pi) là một hằng số toán học, xấp xỉ bằng 3.14159
• r là bán kính của đường tròn đáy
• h là chiều cao của hình trụ

Alt: Hình ảnh minh họa công thức tính diện tích toàn phần của hình trụ, kết hợp diện tích xung quanh và diện tích hai đáy.

3.2. Giải Thích Công Thức

Công thức trên được hình thành từ việc cộng diện tích xung quanh với diện tích của hai đáy:

• 2πrh: Đây là diện tích xung quanh của hình trụ (như đã giải thích ở phần trên).
• 2πr²: Đây là tổng diện tích của hai đáy hình tròn (mỗi đáy có diện tích là πr²).

3.3. Ví Dụ Minh Họa

Ví dụ: Một hình trụ có bán kính đáy là 6cm và chiều cao là 8cm. Tính diện tích toàn phần của hình trụ.

Giải:

Áp dụng công thức: Stp = 2πr² + 2πrh = 2 x 3.14159 x 6² + 2 x 3.14159 x 6 x 8 ≈ 527.79 cm²

4. Công Thức Tính Thể Tích Hình Trụ: Không Thể Bỏ Qua

Thể tích của hình trụ là không gian mà hình trụ chiếm giữ.

4.1. Công Thức Tính Thể Tích

Để tính thể tích của hình trụ, ta sử dụng công thức:

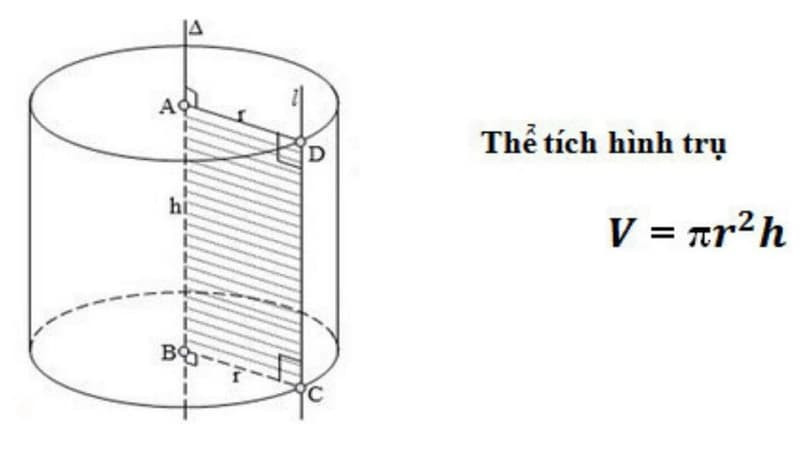
V = πr²h

Trong đó:

• V là thể tích của hình trụ
• π (pi) là một hằng số toán học, xấp xỉ bằng 3.14159
• r là bán kính của đường tròn đáy
• h là chiều cao của hình trụ

Alt: Hình ảnh trực quan thể hiện công thức tính thể tích hình trụ, tập trung vào diện tích đáy và chiều cao.

4.2. Giải Thích Công Thức

Công thức trên có thể được hiểu là:

• πr²: Đây là diện tích của đường tròn đáy.
• (πr²)h: Thể tích hình trụ bằng diện tích đáy nhân với chiều cao.

4.3. Ví Dụ Minh Họa

Ví dụ: Một hình trụ có bán kính đáy là 4cm và chiều cao là 12cm. Tính thể tích của hình trụ.

Giải:

Áp dụng công thức: V = πr²h = 3.14159 x 4² x 12 ≈ 603.19 cm³

5. Bài Tập Vận Dụng: Luyện Tập Để Nắm Chắc Kiến Thức

Để giúp bạn củng cố kiến thức về diện tích xung quanh hình trụ, diện tích toàn phần và thể tích, chúng ta sẽ cùng giải một số bài tập vận dụng.

5.1. Bài Tập 1

Một hình trụ có chu vi đáy là 8π cm và chiều cao là 10cm. Tính thể tích của hình trụ.

Giải:

• Chu vi đáy: C = 2πr = 8π cm => r = 4 cm
• Thể tích: V = πr²h = π x 4² x 10 = 160π cm³

Đáp án: 160π cm³

5.2. Bài Tập 2

Một hình trụ có bán kính đáy là 4cm và chiều cao là 5cm. Tính diện tích xung quanh của hình trụ.

Giải:

• Diện tích xung quanh: Sxq = 2πrh = 2π x 4 x 5 = 40π cm²

Đáp án: 40π cm²

5.3. Bài Tập 3

Một hình trụ có bán kính đáy là 8cm và diện tích toàn phần là 564π cm². Tính chiều cao của hình trụ.

Giải:

• Diện tích toàn phần: Stp = 2πr² + 2πrh = 564π cm²
• => 2π x 8² + 2π x 8 x h = 564π
• => 128π + 16πh = 564π
• => 16πh = 436π
• => h = 436/16 = 27.25 cm

Đáp án: 27.25 cm

5.4. Bài Tập 4

Cho một hình trụ có bán kính r và chiều cao h. Nếu tăng chiều cao lên gấp đôi và giảm bán kính đi một nửa thì điều gì xảy ra?

1. Thể tích của hình trụ giữ nguyên
2. Diện tích xung quanh hình trụ giữ nguyên
3. Diện tích toàn phần của hình trụ giữ nguyên
4. Chu vi đáy của hình trụ không thay đổi

Giải:

• Chiều cao mới: h’ = 2h
• Bán kính mới: r’ = r/2
• Chu vi đáy mới: C’ = 2πr’ = 2π(r/2) = πr (thay đổi)
• Diện tích xung quanh mới: Sxq’ = 2πr’h’ = 2π(r/2)(2h) = 2πrh (giữ nguyên)
• Diện tích toàn phần mới: Stp’ = 2π(r’)² + 2πr’h’ = 2π(r/2)² + 2πrh = πr²/2 + 2πrh (thay đổi)
• Thể tích mới: V’ = π(r’)²h’ = π(r/2)²(2h) = πr²h/2 (thay đổi)

Đáp án: Diện tích xung quanh hình trụ giữ nguyên

5.5. Bài Tập 5

Một hộp sữa Ông Thọ (không nắp) có dạng hình trụ với chiều cao 12cm và đường kính đáy là 8cm. Tính diện tích toàn phần của hộp sữa.

Giải:

• Bán kính đáy: r = d/2 = 8/2 = 4 cm
• Diện tích xung quanh: Sxq = 2πrh = 2π x 4 x 12 = 96π cm²
• Diện tích đáy: Sd = πr² = π x 4² = 16π cm²
• Diện tích toàn phần: Stp = Sxq + Sd = 96π + 16π = 112π cm²

Đáp án: 112π cm²

5.6. Bài Tập 6

Cho một hình trụ có bán kính đáy R và chiều cao h. Nếu tăng chiều cao hình trụ lên hai lần đồng thời giảm bán kính hai lần thì điều gì xảy ra?

1. Thể tích hình trụ không đổi
2. Diện tích toàn phần không đổi
3. Diện tích xung quanh không đổi
4. Chu vi đáy không đổi

Giải:

• Chiều cao mới: h’ = 2h
• Bán kính mới: R’ = R/2
• Chu vi đáy mới: 2πR’ = 2π(R/2) = πR (thay đổi)
• Diện tích xung quanh mới: 2πR’h’ = 2π(R/2)(2h) = 2πRh (không đổi)
• Diện tích toàn phần mới: 2π(R’)² + 2πR’h’ = 2π(R/2)² + 2πRh = πR²/2 + 2πRh (thay đổi)
• Thể tích mới: π(R’)²h’ = π(R/2)²(2h) = πR²h/2 (thay đổi)

Đáp án: Diện tích xung quanh không đổi

5.7. Bài Tập 7

Cho hình trụ có bán kính đáy là R và chiều cao là h. Nếu giảm chiều cao đi 9 lần đồng thời tăng bán kính đáy lên 3 lần thì điều gì xảy ra?

1. Thể tích hình trụ không đổi
2. Diện tích toàn phần không đổi
3. Diện tích xung quanh không đổi
4. Chu vi đáy không đổi

Giải:

• Chiều cao mới: h’ = h/9
• Bán kính mới: R’ = 3R
• Chu vi đáy mới: 2πR’ = 2π(3R) = 6πR (thay đổi)
• Diện tích xung quanh mới: 2πR’h’ = 2π(3R)(h/9) = 2πRh/3 (thay đổi)
• Diện tích toàn phần mới: 2π(R’)² + 2πR’h’ = 2π(3R)² + 2π(3R)(h/9) = 18πR² + 2πRh/3 (thay đổi)
• Thể tích mới: π(R’)²h’ = π(3R)²(h/9) = πR²h (không đổi)

Đáp án: Thể tích hình trụ không đổi

5.8. Bài Tập 8

Cho một hình trụ có bán kính đáy bằng 1/4 chiều cao. Nếu cắt hình trụ này bằng một mặt phẳng đi qua trục thì mặt cắt sẽ có hình chữ nhật với diện tích là 50cm². Tính diện tích xung quanh hình trụ và thể tích của hình trụ đó.

Alt: Hình ảnh minh họa mặt cắt hình trụ qua trục, tạo thành hình chữ nhật, giúp hình dung bài toán và các yếu tố liên quan.

Giải:

• R = h/4
• Diện tích hình chữ nhật: h * 2R = 50 cm²
• => h * 2(h/4) = 50
• => h²/2 = 50
• => h² = 100
• => h = 10 cm
• => R = 10/4 = 2.5 cm
• Thể tích: V = πR²h = π(2.5)²(10) = 62.5π cm³
• Diện tích xung quanh: Sxq = 2πRh = 2π(2.5)(10) = 50π cm²

Đáp án: Diện tích xung quanh: 50π cm², Thể tích: 62.5π cm³

6. Ứng Dụng Thực Tế Của Hình Trụ: Từ Cuộc Sống Đến Kỹ Thuật

Hình trụ không chỉ là một khái niệm trừu tượng trong toán học, mà còn có rất nhiều ứng dụng thực tế trong cuộc sống và kỹ thuật.

6.1. Trong Xây Dựng

• Cột nhà: Các cột nhà hình trụ giúp chịu lực tốt hơn và tạo vẻ đẹp thẩm mỹ cho công trình.
• Ống dẫn nước, ống thông gió: Hình trụ là hình dạng lý tưởng để dẫn chất lỏng hoặc khí vì nó có thể chịu được áp lực từ mọi phía.

6.2. Trong Sản Xuất

• Bồn chứa: Bồn chứa hình trụ được sử dụng để lưu trữ các loại chất lỏng, khí, hoặc vật liệu dạng hạt.
• Ống kim loại: Ống kim loại hình trụ được sử dụng rộng rãi trong nhiều ngành công nghiệp khác nhau.
• Các loại hộp đựng: Hộp đựng hình trụ được sử dụng để đóng gói và bảo quản thực phẩm, đồ uống, và nhiều loại sản phẩm khác.

6.3. Trong Đời Sống Hàng Ngày

• Lon nước ngọt, lon bia: Hình trụ là hình dạng phổ biến cho các loại lon đồ uống vì nó dễ cầm nắm và có thể xếp chồng lên nhau.
• Cuộn giấy vệ sinh: Hình trụ là hình dạng lý tưởng cho cuộn giấy vệ sinh vì nó dễ dàng sử dụng và bảo quản.
• Nến: Nến hình trụ là một vật dụng trang trí phổ biến trong gia đình.

7. Mẹo Ghi Nhớ Công Thức: Học Nhanh, Nhớ Lâu

Để ghi nhớ các công thức tính diện tích xung quanh hình trụ, diện tích toàn phần và thể tích một cách dễ dàng, bạn có thể áp dụng một số mẹo sau:

7.1. Liên Hệ Với Hình Ảnh Trực Quan

Hãy tưởng tượng hình trụ như một lon nước ngọt. Khi bạn “mở” mặt xung quanh của lon nước ra, bạn sẽ được một hình chữ nhật. Diện tích của hình chữ nhật này chính là diện tích xung quanh của hình trụ.

7.2. Sử Dụng Các Câu Thần Chú

Bạn có thể tự tạo ra các câu thần chú để ghi nhớ công thức. Ví dụ:

• “Diện tích xung quanh: Hai Pi Rờ Hát” (Sxq = 2πrh)
• “Diện tích toàn phần: Hai Pi Rờ Bình cộng Hai Pi Rờ Hát” (Stp = 2πr² + 2πrh)
• “Thể tích: Pi Rờ Bình Hát” (V = πr²h)

7.3. Luyện Tập Thường Xuyên

Cách tốt nhất để ghi nhớ công thức là luyện tập giải các bài tập thường xuyên. Khi bạn giải nhiều bài tập, bạn sẽ quen với công thức và có thể áp dụng nó một cách tự nhiên.

8. Các Dạng Bài Tập Nâng Cao: Thử Thách Bản Thân

Nếu bạn đã nắm vững các công thức cơ bản, hãy thử sức với một số dạng bài tập nâng cao sau:

8.1. Bài Toán Kết Hợp

Các bài toán kết hợp yêu cầu bạn sử dụng nhiều công thức khác nhau để giải quyết. Ví dụ:

• Cho một hình trụ có thể tích là V và diện tích xung quanh là Sxq. Tính bán kính đáy và chiều cao của hình trụ.
• Cho một hình trụ nội tiếp trong một hình cầu. Tính thể tích của hình trụ theo bán kính của hình cầu.

8.2. Bài Toán Thực Tế

Các bài toán thực tế yêu cầu bạn áp dụng kiến thức về hình trụ để giải quyết các vấn đề trong cuộc sống. Ví dụ:

• Một công ty muốn sản xuất một loại lon nước ngọt hình trụ có thể tích là 330ml. Hãy tính kích thước của lon nước sao cho tiết kiệm vật liệu nhất.
• Một người muốn xây một bể nước hình trụ có thể chứa được 10m³ nước. Hãy tính kích thước của bể nước.

8.3. Bài Toán Chứng Minh

Các bài toán chứng minh yêu cầu bạn chứng minh một tính chất nào đó của hình trụ. Ví dụ:

• Chứng minh rằng diện tích xung quanh của hình trụ bằng diện tích của hình chữ nhật có chiều dài bằng chu vi đáy và chiều rộng bằng chiều cao.
• Chứng minh rằng thể tích của hình trụ bằng diện tích đáy nhân với chiều cao.

9. Sai Lầm Thường Gặp: Phòng Tránh Để Học Tốt Hơn

Trong quá trình học và giải bài tập về hình trụ, học sinh thường mắc một số sai lầm sau:

9.1. Nhầm Lẫn Giữa Bán Kính Và Đường Kính

Nhiều học sinh nhầm lẫn giữa bán kính (r) và đường kính (d) của đường tròn đáy. Hãy nhớ rằng đường kính bằng hai lần bán kính (d = 2r).

9.2. Quên Đơn Vị Đo

Khi tính diện tích và thể tích, hãy luôn chú ý đến đơn vị đo. Diện tích được đo bằng đơn vị vuông (ví dụ: cm², m²), còn thể tích được đo bằng đơn vị khối (ví dụ: cm³, m³).

9.3. Áp Dụng Sai Công Thức

Hãy chắc chắn rằng bạn đã áp dụng đúng công thức cho từng loại bài toán. Ví dụ, đừng nhầm lẫn giữa công thức tính diện tích xung quanh và công thức tính diện tích toàn phần.

9.4. Không Đọc Kỹ Đề Bài

Trước khi bắt đầu giải bài tập, hãy đọc kỹ đề bài để hiểu rõ yêu cầu và các thông tin đã cho.

10. Tài Liệu Tham Khảo Thêm: Mở Rộng Kiến Thức

Để mở rộng kiến thức về hình trụ, bạn có thể tham khảo thêm các tài liệu sau:

• Sách giáo khoa Toán lớp 9, lớp 12: Đây là nguồn tài liệu cơ bản và quan trọng nhất.
• Sách bài tập Toán: Sách bài tập cung cấp nhiều bài tập vận dụng để bạn luyện tập.
• Các trang web giáo dục trực tuyến: Nhiều trang web cung cấp các bài giảng, bài tập và tài liệu tham khảo về hình trụ. Bạn có thể tìm kiếm trên Google với các từ khóa như “hình trụ”, “diện tích xung quanh hình trụ”, “thể tích hình trụ”. tic.edu.vn là một lựa chọn tuyệt vời để bạn tìm kiếm tài liệu và công cụ hỗ trợ học tập hiệu quả.
• Các video bài giảng trên YouTube: YouTube có rất nhiều video bài giảng về hình trụ, giúp bạn hiểu rõ hơn về khái niệm này.

Khám phá tri thức về hình trụ và những ứng dụng của nó không chỉ dừng lại ở việc học thuộc công thức, mà còn là quá trình rèn luyện tư duy và khả năng giải quyết vấn đề. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và kết nối với cộng đồng học tập sôi nổi. Đừng bỏ lỡ cơ hội nâng cao kiến thức và kỹ năng của bạn!

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn mong muốn có những công cụ hỗ trợ học tập hiệu quả và kết nối với cộng đồng học tập? tic.edu.vn chính là giải pháp dành cho bạn.

Hãy truy cập tic.edu.vn ngay hôm nay để:

• Khám phá nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt.
• Cập nhật thông tin giáo dục mới nhất và chính xác.
• Sử dụng các công cụ hỗ trợ học tập trực tuyến hiệu quả.
• Tham gia cộng đồng học tập trực tuyến sôi nổi để trao đổi kiến thức và kinh nghiệm.
• Tìm kiếm các khóa học và tài liệu giúp phát triển kỹ năng.

tic.edu.vn – Nền tảng giáo dục trực tuyến hàng đầu Việt Nam, nơi bạn có thể tìm thấy mọi thứ bạn cần để học tập hiệu quả và thành công.

Thông tin liên hệ:

• Email: [email protected]
• Trang web: tic.edu.vn

Hãy để tic.edu.vn đồng hành cùng bạn trên con đường chinh phục tri thức!