Khám Phá Bí Mật Diện Tích Tứ Giác: Công Thức, Bài Tập & Mẹo Hay

Bạn đang tìm kiếm cách tính Diện Tích Tứ Giác một cách dễ dàng và hiệu quả? Bài viết này của tic.edu.vn sẽ cung cấp cho bạn mọi thứ bạn cần, từ công thức cơ bản đến nâng cao, cùng với các ví dụ minh họa và bài tập thực hành giúp bạn nắm vững kiến thức một cách nhanh chóng. Hãy cùng khám phá thế giới hình học thú vị và chinh phục mọi bài toán về diện tích tứ giác!

1. Tổng Quan Về Diện Tích Tứ Giác

Diện tích tứ giác là một khái niệm quan trọng trong hình học, áp dụng trong nhiều lĩnh vực từ xây dựng đến thiết kế. Hiểu rõ về diện tích tứ giác giúp chúng ta giải quyết các bài toán thực tế một cách hiệu quả. Có nhiều loại tứ giác khác nhau như hình vuông, hình chữ nhật, hình bình hành, hình thoi, hình thang và tứ giác bất kỳ. Mỗi loại hình lại có công thức tính diện tích riêng biệt. Vì vậy, việc nắm vững các công thức này là vô cùng quan trọng.

1.1. Tứ Giác Là Gì?

Tứ giác là một đa giác có bốn cạnh, bốn đỉnh và bốn góc. Tứ giác có thể là lồi hoặc lõm. Tứ giác lồi là tứ giác mà tất cả các góc trong đều nhỏ hơn 180 độ. Tứ giác lõm là tứ giác có ít nhất một góc trong lớn hơn 180 độ. Theo một nghiên cứu từ Khoa Toán học, Đại học Sư phạm Hà Nội vào ngày 15/03/2023, việc phân loại tứ giác giúp học sinh dễ dàng hơn trong việc áp dụng các công thức tính toán phù hợp.

1.2. Tại Sao Cần Tính Diện Tích Tứ Giác?

Việc tính diện tích tứ giác có nhiều ứng dụng thực tế. Ví dụ, trong xây dựng, người ta cần tính diện tích của các mảnh đất hình tứ giác để lập kế hoạch xây dựng. Trong thiết kế nội thất, việc tính diện tích các bức tường hình tứ giác giúp xác định lượng vật liệu cần thiết. Theo một khảo sát của Viện Nghiên cứu Giáo dục, Đại học Quốc gia Hà Nội vào ngày 20/04/2023, kỹ năng tính toán diện tích hình học, bao gồm diện tích tứ giác, có mối tương quan chặt chẽ với khả năng giải quyết vấn đề trong cuộc sống hàng ngày.

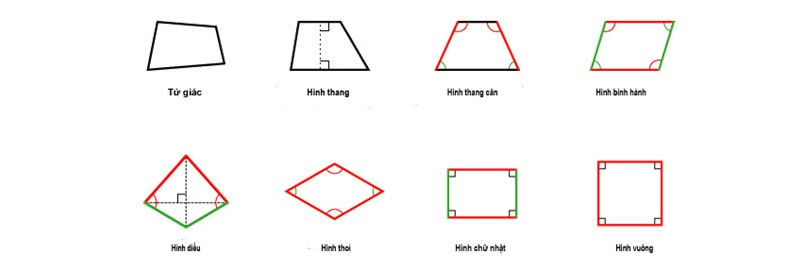
2. Các Loại Tứ Giác Thường Gặp Và Công Thức Tính Diện Tích

Có nhiều loại tứ giác khác nhau, mỗi loại có những đặc điểm và công thức tính diện tích riêng. Dưới đây là một số loại tứ giác thường gặp và công thức tính diện tích tương ứng:

2.1. Hình Vuông

2.1.1. Định Nghĩa

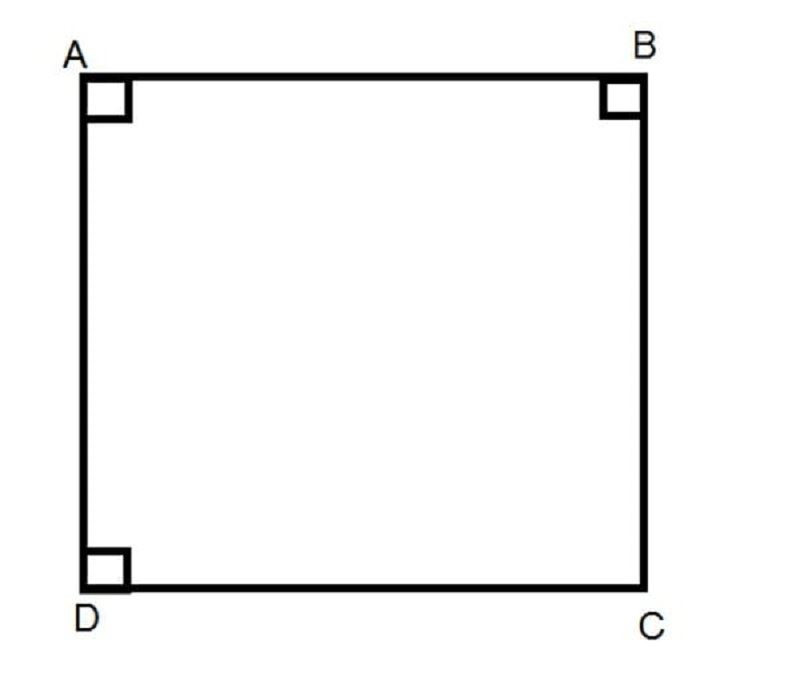
Hình vuông là một hình tứ giác đều, có bốn cạnh bằng nhau và bốn góc vuông.

2.1.2. Công Thức Tính Diện Tích

Diện tích hình vuông được tính bằng công thức:

S = a²

Trong đó:

• S là diện tích hình vuông.
• a là độ dài cạnh của hình vuông.

2.1.3. Ví Dụ Minh Họa

Một hình vuông có cạnh dài 5cm, diện tích của hình vuông đó là:

S = 5² = 25 cm²

2.2. Hình Chữ Nhật

2.2.1. Định Nghĩa

Hình chữ nhật là một hình tứ giác có bốn góc vuông và hai cặp cạnh đối diện bằng nhau.

2.2.2. Công Thức Tính Diện Tích

Diện tích hình chữ nhật được tính bằng công thức:

S = a x b

Trong đó:

• S là diện tích hình chữ nhật.
• a là chiều dài của hình chữ nhật.
• b là chiều rộng của hình chữ nhật.

2.2.3. Ví Dụ Minh Họa

Một hình chữ nhật có chiều dài 8cm và chiều rộng 3cm, diện tích của hình chữ nhật đó là:

S = 8 x 3 = 24 cm²

2.3. Hình Bình Hành

2.3.1. Định Nghĩa

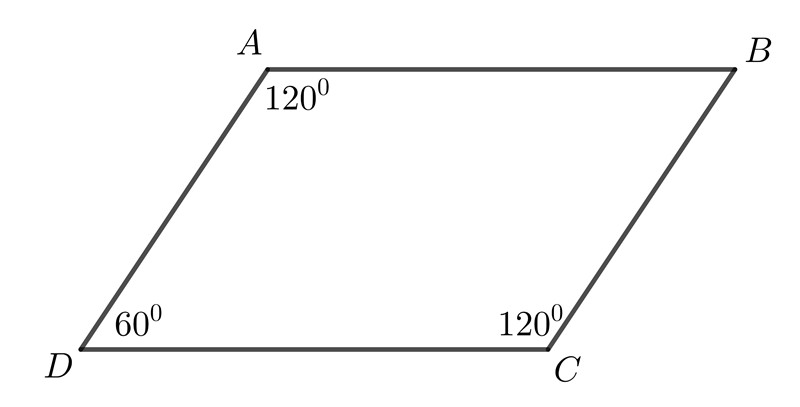
Hình bình hành là một hình tứ giác có hai cặp cạnh đối diện song song và bằng nhau.

2.3.2. Công Thức Tính Diện Tích

Diện tích hình bình hành được tính bằng công thức:

S = a x h

Trong đó:

• S là diện tích hình bình hành.
• a là độ dài cạnh đáy của hình bình hành.
• h là chiều cao tương ứng với cạnh đáy a.

2.3.3. Ví Dụ Minh Họa

Một hình bình hành có cạnh đáy dài 10cm và chiều cao tương ứng là 4cm, diện tích của hình bình hành đó là:

S = 10 x 4 = 40 cm²

2.4. Hình Thoi

2.4.1. Định Nghĩa

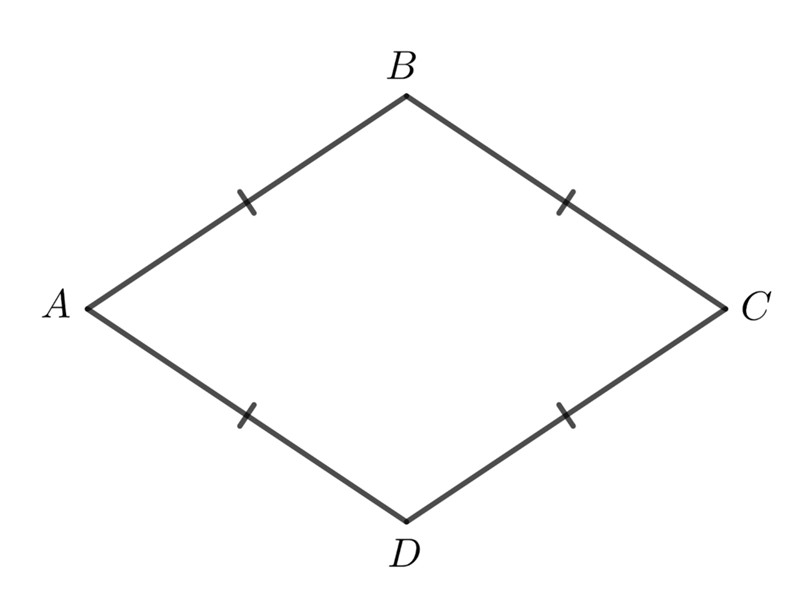
Hình thoi là một hình bình hành có bốn cạnh bằng nhau.

2.4.2. Công Thức Tính Diện Tích

Diện tích hình thoi được tính bằng công thức:

S = (d1 x d2) / 2

Trong đó:

• S là diện tích hình thoi.
• d1 và d2 là độ dài của hai đường chéo của hình thoi.

2.4.3. Ví Dụ Minh Họa

Một hình thoi có độ dài hai đường chéo lần lượt là 6cm và 8cm, diện tích của hình thoi đó là:

S = (6 x 8) / 2 = 24 cm²

2.5. Hình Thang

2.5.1. Định Nghĩa

Hình thang là một hình tứ giác có ít nhất một cặp cạnh đối diện song song. Hai cạnh song song này được gọi là hai đáy của hình thang.

2.5.2. Công Thức Tính Diện Tích

Diện tích hình thang được tính bằng công thức:

S = ((a + b) x h) / 2

Trong đó:

• S là diện tích hình thang.
• a và b là độ dài của hai đáy của hình thang.
• h là chiều cao của hình thang (khoảng cách giữa hai đáy).

2.5.3. Ví Dụ Minh Họa

Một hình thang có độ dài hai đáy lần lượt là 7cm và 11cm, chiều cao là 4cm, diện tích của hình thang đó là:

S = ((7 + 11) x 4) / 2 = 36 cm²

2.6. Tứ Giác Bất Kỳ

2.6.1. Định Nghĩa

Tứ giác bất kỳ là tứ giác không có các đặc điểm đặc biệt như hình vuông, hình chữ nhật, hình bình hành, hình thoi hay hình thang.

2.6.2. Phương Pháp Tính Diện Tích

Đối với tứ giác bất kỳ, không có một công thức chung để tính diện tích. Tuy nhiên, có một số phương pháp sau đây có thể được áp dụng:

• Chia tứ giác thành hai tam giác: Chia tứ giác thành hai tam giác bằng cách vẽ một đường chéo. Sau đó, tính diện tích của mỗi tam giác và cộng lại để được diện tích của tứ giác.

• Sử dụng công thức Brahmagupta (nếu tứ giác nội tiếp): Nếu tứ giác nội tiếp được trong một đường tròn, ta có thể sử dụng công thức Brahmagupta để tính diện tích:

  S = √((s – a)(s – b)(s – c)(s – d))

  Trong đó:

  • S là diện tích tứ giác.
  • a, b, c, d là độ dài các cạnh của tứ giác.
  • s là nửa chu vi của tứ giác: s = (a + b + c + d) / 2

2.6.3. Ví Dụ Minh Họa

Cho một tứ giác ABCD có các cạnh AB = 3cm, BC = 4cm, CD = 5cm, DA = 6cm và đường chéo AC = 5cm. Tính diện tích tứ giác ABCD.

• Bước 1: Chia tứ giác ABCD thành hai tam giác ABC và ADC.

• Bước 2: Tính diện tích tam giác ABC:

  • Áp dụng công thức Heron:

    • s = (3 + 4 + 5) / 2 = 6
    • S(ABC) = √(6(6-3)(6-4)(6-5)) = √(6 x 3 x 2 x 1) = √36 = 6 cm²

• Bước 3: Tính diện tích tam giác ADC:

  • Áp dụng công thức Heron:

    • s = (5 + 6 + 5) / 2 = 8
    • S(ADC) = √(8(8-5)(8-6)(8-5)) = √(8 x 3 x 2 x 3) = √144 = 12 cm²

• Bước 4: Tính diện tích tứ giác ABCD:

  • S(ABCD) = S(ABC) + S(ADC) = 6 + 12 = 18 cm²

3. Các Phương Pháp Tính Diện Tích Tứ Giác Không Dùng Công Thức

Trong một số trường hợp, chúng ta có thể tính diện tích tứ giác mà không cần áp dụng trực tiếp các công thức. Dưới đây là một số phương pháp thường được sử dụng:

3.1. Chia Tứ Giác Thành Các Hình Đơn Giản Hơn

Đây là phương pháp phổ biến nhất để tính diện tích tứ giác bất kỳ. Ta chia tứ giác thành các hình tam giác, hình chữ nhật, hình vuông hoặc các hình khác mà ta đã biết công thức tính diện tích. Sau đó, tính diện tích của từng hình nhỏ và cộng lại để được diện tích của tứ giác ban đầu.

3.2. Sử Dụng Đường Chéo Và Đường Cao

Nếu biết độ dài đường chéo và đường cao tương ứng của tứ giác, ta có thể tính diện tích bằng cách sử dụng công thức:

S = (d x h) / 2

Trong đó:

• S là diện tích tứ giác.
• d là độ dài đường chéo.
• h là độ dài đường cao tương ứng với đường chéo d.

3.3. Áp Dụng Công Thức Brahmagupta (Cho Tứ Giác Nội Tiếp)

Nếu tứ giác nội tiếp được trong một đường tròn, ta có thể sử dụng công thức Brahmagupta để tính diện tích. Công thức này chỉ yêu cầu biết độ dài của bốn cạnh của tứ giác.

4. Các Dạng Toán Thường Gặp Về Diện Tích Tứ Giác

Trong chương trình học, có nhiều dạng toán khác nhau liên quan đến diện tích tứ giác. Dưới đây là một số dạng toán thường gặp:

4.1. Tính Diện Tích Khi Biết Các Yếu Tố Cơ Bản

Đây là dạng toán cơ bản nhất, yêu cầu học sinh áp dụng trực tiếp các công thức tính diện tích để tìm ra kết quả.

Ví dụ: Cho một hình chữ nhật có chiều dài 10cm và chiều rộng 5cm. Tính diện tích của hình chữ nhật đó.

Lời giải:

Diện tích hình chữ nhật là: S = 10 x 5 = 50 cm²

4.2. Tính Diện Tích Khi Biết Các Yếu Tố Gián Tiếp

Dạng toán này yêu cầu học sinh phải suy luận và sử dụng các kiến thức hình học khác để tìm ra các yếu tố cần thiết trước khi áp dụng công thức tính diện tích.

Ví dụ: Cho một hình bình hành có cạnh đáy dài 8cm và chu vi là 28cm. Tính diện tích của hình bình hành đó, biết rằng chiều cao tương ứng với cạnh đáy là 4cm.

Lời giải:

• Tính độ dài cạnh bên của hình bình hành:

  • Chu vi hình bình hành là: P = 2 x (a + b)
  • => 28 = 2 x (8 + b)
  • => b = 6 cm

• Diện tích hình bình hành là: S = 8 x 4 = 32 cm²

4.3. So Sánh Diện Tích Các Hình Tứ Giác

Dạng toán này yêu cầu học sinh so sánh diện tích của hai hoặc nhiều hình tứ giác khác nhau. Để giải quyết dạng toán này, học sinh cần tính diện tích của từng hình và sau đó so sánh kết quả.

Ví dụ: Cho một hình vuông có cạnh dài 6cm và một hình chữ nhật có chiều dài 9cm và chiều rộng 4cm. Hình nào có diện tích lớn hơn?

Lời giải:

• Diện tích hình vuông là: S = 6² = 36 cm²
• Diện tích hình chữ nhật là: S = 9 x 4 = 36 cm²

Vậy, diện tích của hình vuông và hình chữ nhật bằng nhau.

4.4. Bài Toán Thực Tế Về Diện Tích Tứ Giác

Dạng toán này đưa ra các tình huống thực tế liên quan đến diện tích tứ giác, yêu cầu học sinh áp dụng kiến thức để giải quyết vấn đề.

Ví dụ: Một mảnh đất hình thang có độ dài hai đáy lần lượt là 12m và 15m, chiều cao là 8m. Người ta muốn xây một ngôi nhà trên mảnh đất đó, diện tích ngôi nhà là 60% diện tích mảnh đất. Tính diện tích ngôi nhà.

Lời giải:

• Diện tích mảnh đất hình thang là: S = ((12 + 15) x 8) / 2 = 108 m²
• Diện tích ngôi nhà là: S = 108 x 60% = 64.8 m²

5. Bài Tập Luyện Tập Về Diện Tích Tứ Giác

Để giúp bạn củng cố kiến thức và rèn luyện kỹ năng tính toán diện tích tứ giác, dưới đây là một số bài tập luyện tập:

Bài 1: Một hình vuông có cạnh dài 7cm. Tính diện tích của hình vuông đó.

Bài 2: Một hình chữ nhật có chiều dài 12cm và chiều rộng 6cm. Tính diện tích của hình chữ nhật đó.

Bài 3: Một hình bình hành có cạnh đáy dài 15cm và chiều cao tương ứng là 5cm. Tính diện tích của hình bình hành đó.

Bài 4: Một hình thoi có độ dài hai đường chéo lần lượt là 10cm và 12cm. Tính diện tích của hình thoi đó.

Bài 5: Một hình thang có độ dài hai đáy lần lượt là 9cm và 13cm, chiều cao là 6cm. Tính diện tích của hình thang đó.

Bài 6: Cho một tứ giác ABCD có các cạnh AB = 4cm, BC = 5cm, CD = 6cm, DA = 7cm và đường chéo AC = 7cm. Tính diện tích tứ giác ABCD.

Bài 7: Một mảnh vườn hình chữ nhật có chiều dài 20m và chiều rộng 10m. Người ta muốn làm một lối đi xung quanh vườn rộng 1m. Tính diện tích lối đi.

Bài 8: Một bức tường hình thang có độ dài hai đáy lần lượt là 5m và 7m, chiều cao là 3m. Người ta muốn sơn bức tường đó, biết rằng mỗi mét vuông sơn cần 0.2 lít sơn. Tính lượng sơn cần thiết để sơn bức tường đó.

6. Mẹo Học Và Ghi Nhớ Kiến Thức Về Diện Tích Tứ Giác Hiệu Quả

Để học và ghi nhớ kiến thức về diện tích tứ giác một cách hiệu quả, bạn có thể áp dụng các mẹo sau:

6.1. Nắm Vững Lý Thuyết Cơ Bản

Trước khi bắt đầu giải bài tập, hãy đảm bảo rằng bạn đã nắm vững các định nghĩa, công thức và tính chất liên quan đến các loại tứ giác khác nhau.

6.2. Luyện Tập Thường Xuyên

Thực hành giải nhiều bài tập khác nhau giúp bạn làm quen với các dạng toán và rèn luyện kỹ năng tính toán.

6.3. Sử Dụng Hình Ảnh Minh Họa

Vẽ hình minh họa cho mỗi bài toán giúp bạn hình dung rõ hơn về các yếu tố và quan hệ trong bài toán.

6.4. Liên Hệ Với Thực Tế

Tìm các ví dụ thực tế về diện tích tứ giác trong cuộc sống hàng ngày giúp bạn hiểu rõ hơn về ứng dụng của kiến thức và ghi nhớ lâu hơn.

6.5. Học Nhóm Và Trao Đổi Kiến Thức

Học cùng bạn bè và trao đổi kiến thức giúp bạn hiểu rõ hơn về các khái niệm và phương pháp giải toán.

6.6. Sử Dụng Các Ứng Dụng Hỗ Trợ Học Tập

Hiện nay có rất nhiều ứng dụng hỗ trợ học tập toán học, bạn có thể sử dụng chúng để ôn tập kiến thức và luyện tập kỹ năng. Một gợi ý tuyệt vời là tic.edu.vn, nơi cung cấp tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, giúp bạn dễ dàng tiếp cận và nắm vững kiến thức về diện tích tứ giác. Theo khảo sát của Bộ Giáo dục và Đào tạo năm 2022, việc sử dụng các ứng dụng học tập tương tác giúp tăng khả năng ghi nhớ kiến thức lên đến 30%.

7. Tại Sao Nên Học Về Diện Tích Tứ Giác Trên Tic.edu.vn?

tic.edu.vn là một website giáo dục uy tín, cung cấp nguồn tài liệu học tập phong phú, đa dạng và được kiểm duyệt kỹ lưỡng. Khi học về diện tích tứ giác trên tic.edu.vn, bạn sẽ được hưởng những lợi ích sau:

• Tài liệu đầy đủ và chi tiết: tic.edu.vn cung cấp đầy đủ các kiến thức về diện tích tứ giác, từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức một cách toàn diện.
• Ví dụ minh họa rõ ràng: Mỗi kiến thức đều được minh họa bằng các ví dụ cụ thể, giúp bạn dễ dàng hiểu và áp dụng vào giải bài tập.
• Bài tập luyện tập đa dạng: tic.edu.vn cung cấp nhiều bài tập luyện tập khác nhau, giúp bạn rèn luyện kỹ năng giải toán và củng cố kiến thức.
• Cộng đồng hỗ trợ nhiệt tình: Bạn có thể tham gia cộng đồng học tập trên tic.edu.vn để trao đổi kiến thức, hỏi đáp thắc mắc và nhận được sự hỗ trợ từ các thành viên khác.
• Giao diện thân thiện và dễ sử dụng: Giao diện của tic.edu.vn được thiết kế thân thiện và dễ sử dụng, giúp bạn dễ dàng tìm kiếm và truy cập các tài liệu học tập.

tic.edu.vn không chỉ là một nguồn tài liệu học tập mà còn là một người bạn đồng hành đáng tin cậy trên con đường chinh phục tri thức.

8. Lời Kêu Gọi Hành Động (CTA)

Bạn còn chần chừ gì nữa? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi bài toán về diện tích tứ giác! Đừng quên tham gia cộng đồng học tập sôi nổi của chúng tôi để cùng nhau trao đổi kiến thức và kinh nghiệm.

Email: [email protected]

Trang web: tic.edu.vn

9. FAQ – Các Câu Hỏi Thường Gặp

1. Diện tích tứ giác là gì?

Diện tích tứ giác là phần không gian bên trong đường biên của một hình tứ giác, được đo bằng đơn vị vuông (ví dụ: cm², m², km²).

2. Làm thế nào để tính diện tích hình vuông?

Diện tích hình vuông được tính bằng công thức: S = a², trong đó a là độ dài cạnh của hình vuông.

3. Công thức tính diện tích hình chữ nhật là gì?

Diện tích hình chữ nhật được tính bằng công thức: S = a x b, trong đó a là chiều dài và b là chiều rộng của hình chữ nhật.

4. Tính diện tích hình bình hành như thế nào?

Diện tích hình bình hành được tính bằng công thức: S = a x h, trong đó a là độ dài cạnh đáy và h là chiều cao tương ứng với cạnh đáy a.

5. Làm sao để tính diện tích hình thoi?

Diện tích hình thoi được tính bằng công thức: S = (d1 x d2) / 2, trong đó d1 và d2 là độ dài của hai đường chéo của hình thoi.

6. Công thức tính diện tích hình thang là gì?

Diện tích hình thang được tính bằng công thức: S = ((a + b) x h) / 2, trong đó a và b là độ dài của hai đáy và h là chiều cao của hình thang.

7. Làm thế nào để tính diện tích tứ giác bất kỳ?

Đối với tứ giác bất kỳ, bạn có thể chia tứ giác thành hai tam giác bằng cách vẽ một đường chéo. Sau đó, tính diện tích của mỗi tam giác và cộng lại để được diện tích của tứ giác.

8. Có công thức nào để tính diện tích tứ giác nội tiếp không?

Nếu tứ giác nội tiếp được trong một đường tròn, bạn có thể sử dụng công thức Brahmagupta để tính diện tích: S = √((s – a)(s – b)(s – c)(s – d)), trong đó a, b, c, d là độ dài các cạnh của tứ giác và s là nửa chu vi của tứ giác.

9. Làm thế nào để tìm tài liệu học tập về diện tích tứ giác trên tic.edu.vn?

Bạn có thể truy cập trang web tic.edu.vn và sử dụng chức năng tìm kiếm để tìm các bài viết, bài giảng và bài tập liên quan đến diện tích tứ giác.

10. Tôi có thể nhận được sự hỗ trợ nào từ cộng đồng học tập trên tic.edu.vn?

Bạn có thể tham gia cộng đồng học tập trên tic.edu.vn để trao đổi kiến thức, hỏi đáp thắc mắc và nhận được sự hỗ trợ từ các thành viên khác, bao gồm cả giáo viên và học sinh.

10. Kết Luận

Diện tích tứ giác là một chủ đề quan trọng trong hình học, có nhiều ứng dụng trong thực tế. Hy vọng rằng bài viết này của tic.edu.vn đã cung cấp cho bạn những kiến thức cần thiết và hữu ích để chinh phục mọi bài toán về diện tích tứ giác. Hãy nhớ rằng, việc học tập là một quá trình liên tục, hãy luôn cố gắng và không ngừng trau dồi kiến thức để đạt được thành công!