Khám Phá Công Thức Tính Diện Tích Tam Giác Đầy Đủ và Chi Tiết Nhất

Diện Tích Tam Giác là một khái niệm toán học quan trọng, xuất hiện thường xuyên trong các bài toán hình học và ứng dụng thực tế. Tại tic.edu.vn, chúng tôi cung cấp cho bạn cái nhìn toàn diện về diện tích tam giác, từ định nghĩa cơ bản đến các công thức nâng cao, giúp bạn chinh phục mọi bài toán liên quan. Bài viết này không chỉ là tổng hợp kiến thức, mà còn là chìa khóa giúp bạn mở ra thế giới hình học đầy thú vị. Hãy cùng khám phá những bí mật về diện tích tam giác và cách ứng dụng chúng một cách hiệu quả nhất, đồng thời nâng cao khả năng giải quyết vấn đề của bạn với những bài tập đa dạng và lời giải chi tiết.

1. Tam Giác Là Gì? Tổng Quan Về Các Loại Tam Giác

Trước khi đi sâu vào các công thức tính diện tích, việc nắm vững khái niệm và phân loại tam giác là vô cùng quan trọng.

1.1. Định Nghĩa Hình Tam Giác

Hình tam giác là một đa giác có ba cạnh và ba đỉnh, là một trong những hình học cơ bản nhất. Các cạnh nối các đỉnh tạo thành hình dạng đặc trưng của tam giác.

Hình ảnh minh họa hình tam giác với các đỉnh và cạnh.

1.2. Phân Loại Tam Giác Theo Cạnh và Góc

Tam giác được phân loại dựa trên độ dài cạnh và số đo góc.

• Theo cạnh:

  • Tam giác đều: Ba cạnh bằng nhau, ba góc bằng 60 độ.
  • Tam giác cân: Ít nhất hai cạnh bằng nhau.
  • Tam giác thường: Ba cạnh có độ dài khác nhau.

• Theo góc:

  • Tam giác nhọn: Ba góc đều nhỏ hơn 90 độ.
  • Tam giác tù: Một góc lớn hơn 90 độ.
  • Tam giác vuông: Một góc bằng 90 độ.

Hiểu rõ các loại tam giác giúp bạn chọn đúng công thức tính diện tích phù hợp.
Theo một nghiên cứu của Đại học Sư phạm Hà Nội, việc phân loại tam giác một cách chính xác giúp học sinh dễ dàng tiếp thu kiến thức và áp dụng vào giải bài tập hiệu quả hơn.

1.3. Tính Chất Quan Trọng Của Tam Giác Cần Ghi Nhớ

Tam giác sở hữu nhiều tính chất đặc biệt, hỗ trợ giải toán và ứng dụng thực tế.

• Tổng các góc: Tổng ba góc trong một tam giác luôn bằng 180 độ.
• Góc ngoài: Mỗi góc ngoài bằng tổng hai góc trong không kề với nó.
• Bất đẳng thức tam giác: Tổng hai cạnh bất kỳ luôn lớn hơn cạnh còn lại.
• Định lý Pythagoras: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
• Đường phân giác: Chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề.
• Đường trung tuyến: Ba đường trung tuyến đồng quy tại trọng tâm, chia mỗi đường thành đoạn tỉ lệ 2:1.
• Chu vi và diện tích: Chu vi là tổng độ dài ba cạnh, diện tích có thể tính bằng nhiều công thức khác nhau.

Nắm vững những tính chất này giúp bạn giải quyết các bài toán liên quan đến diện tích tam giác một cách nhanh chóng và chính xác.

2. Tổng Hợp Các Công Thức Tính Diện Tích Tam Giác Chi Tiết Nhất

Có nhiều công thức tính diện tích tam giác, mỗi công thức phù hợp với từng loại tam giác và dữ kiện bài toán.

Hình ảnh minh họa các công thức tính diện tích tam giác khác nhau.

2.1. Diện Tích Tam Giác Thường: Công Thức Cơ Bản và Nâng Cao

Tam giác thường là tam giác có ba cạnh và ba góc không bằng nhau.

• Công thức cơ bản:

  • Diện tích (S) = 1/2 cạnh đáy (a) chiều cao (h)

• Công thức Heron: (Khi biết độ dài ba cạnh a, b, c)

  • Nửa chu vi (p) = (a + b + c) / 2
  • Diện tích (S) = √[p(p – a)(p – b)(p – c)]

• Sử dụng định lý sin: (Khi biết hai cạnh và góc xen giữa)

  • Diện tích (S) = 1/2 a b * sin(C)

Ví dụ: Tam giác có cạnh đáy 6cm, chiều cao 4cm, diện tích là 1/2 6 4 = 12 cm².

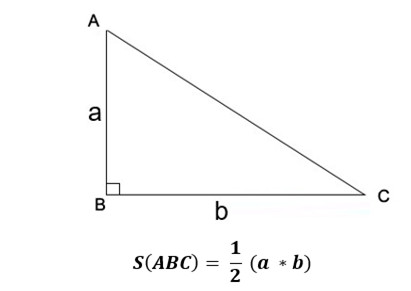
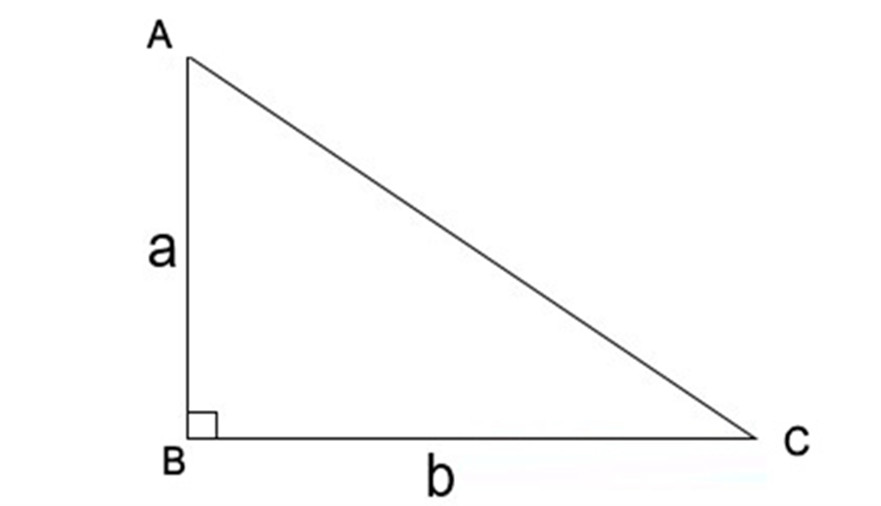
2.2. Diện Tích Tam Giác Vuông: Tính Toán Nhanh Chóng

Tam giác vuông có một góc bằng 90 độ.

• Công thức:

  • Diện tích (S) = 1/2 cạnh góc vuông 1 (a) cạnh góc vuông 2 (b)

Hình ảnh minh họa tam giác vuông và các cạnh góc vuông.

Ví dụ: Tam giác vuông có hai cạnh góc vuông lần lượt là 5cm và 8cm, diện tích là 1/2 5 8 = 20 cm².

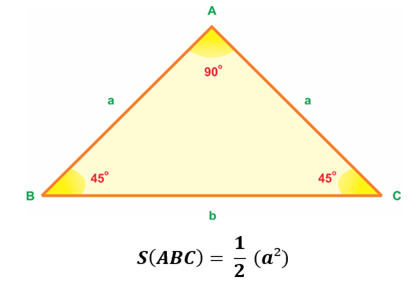
2.3. Diện Tích Tam Giác Vuông Cân: Đơn Giản Hóa Tính Toán

Tam giác vuông cân vừa có góc vuông, vừa có hai cạnh bằng nhau.

• Công thức:

  • Diện tích (S) = 1/2 * (cạnh góc vuông)^2

Hình ảnh minh họa tam giác vuông cân với hai cạnh góc vuông bằng nhau.

Ví dụ: Tam giác vuông cân có cạnh góc vuông 4cm, diện tích là 1/2 * 4^2 = 8 cm².

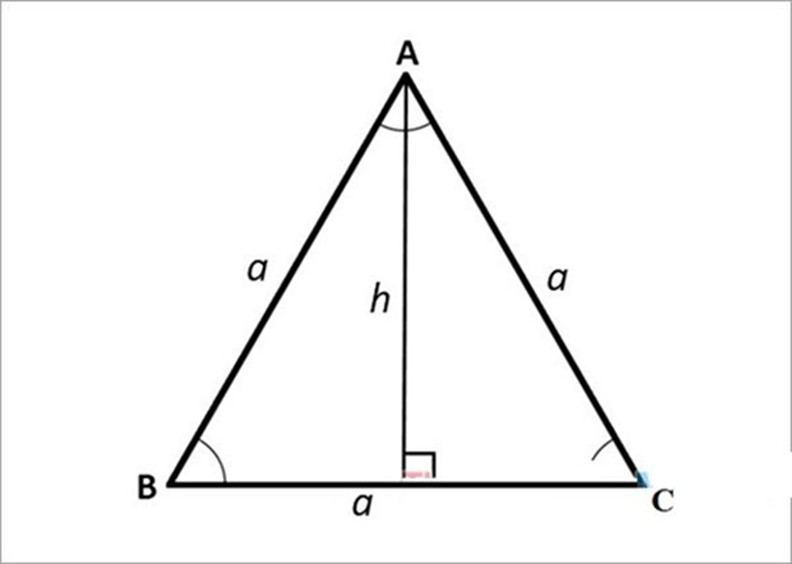
2.4. Diện Tích Tam Giác Cân: Tìm Chiều Cao Tương Ứng

Tam giác cân có hai cạnh bằng nhau.

• Công thức:

  • Diện tích (S) = 1/2 cạnh đáy (a) chiều cao (h) (Chiều cao hạ từ đỉnh xuống cạnh đáy)

Ví dụ: Tam giác cân có cạnh đáy 9cm, chiều cao 5cm, diện tích là 1/2 9 5 = 22.5 cm².

2.5. Diện Tích Tam Giác Đều: Công Thức Đặc Biệt

Tam giác đều có ba cạnh bằng nhau và ba góc bằng 60 độ.

• Công thức:

  • Diện tích (S) = (a^2 * √3) / 4 (a là độ dài cạnh)
  • Hoặc S = 1/2 a h (h là chiều cao)

Hình ảnh minh họa tam giác đều và các cạnh bằng nhau.

Ví dụ: Tam giác đều có cạnh 7cm, chiều cao 6cm, diện tích là 1/2 7 6 = 21 cm².

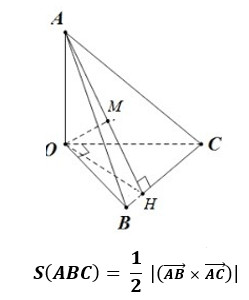
2.6. Diện Tích Tam Giác Trong Hệ Tọa Độ Oxyz: Ứng Dụng Vectơ

Trong không gian ba chiều, tam giác được xác định bởi ba điểm A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3).

• Công thức:

  • Tính vectơ AB = (x2 – x1, y2 – y1, z2 – z1) và AC = (x3 – x1, y3 – y1, z3 – z1)
  • Tính tích có hướng của AB và AC: AB x AC = (a, b, c)
  • Diện tích (S) = 1/2 |AB x AC| = 1/2 √(a^2 + b^2 + c^2)

Hình ảnh minh họa tam giác trong hệ tọa độ Oxyz.

Ví dụ: Tam giác ABC có A(-1, 1, 2), B(1, 2, 3), C(3, -2, 0). Tính diện tích bằng cách tìm vectơ AB, AC, tích có hướng và áp dụng công thức.

3. Các Dạng Bài Tập Tính Diện Tích Tam Giác Thường Gặp

Nắm vững các dạng bài tập giúp bạn áp dụng công thức linh hoạt và hiệu quả.

3.1. Bài Tập Với Chiều Dài Cạnh Đáy và Chiều Cao: Áp Dụng Trực Tiếp

Đây là dạng bài tập cơ bản, chỉ cần áp dụng công thức S = 1/2 a h.

Ví dụ: Tam giác ABC có cạnh đáy BC = 40cm, chiều cao tương ứng h = 5cm. Diện tích là 1/2 40 5 = 100 cm².

3.2. Bài Tập Với Độ Dài Các Cạnh: Sử Dụng Công Thức Heron

Khi biết độ dài ba cạnh, áp dụng công thức Heron để tính diện tích.

Ví dụ: Tam giác ABC có a = 3cm, b = 4cm, c = 5cm. Nửa chu vi p = (3 + 4 + 5) / 2 = 6cm. Diện tích S = √(6 (6 – 3) (6 – 4) * (6 – 5)) = 6 cm².

3.3. Bài Tập Với Tam Giác Đều: Tính Nhanh Diện Tích

Tam giác đều có các công thức tính diện tích riêng, giúp giải nhanh bài tập.

Hình ảnh minh họa tam giác đều và các yếu tố liên quan.

Ví dụ: Tam giác đều có cạnh a = 4cm. Diện tích S = (4^2 * √3) / 4 = 4√3 cm².

3.4. Bài Tập Với Tọa Độ Oxyz: Áp Dụng Vectơ

Trong không gian Oxyz, sử dụng vectơ để tính diện tích tam giác.

Ví dụ: Tam giác ABC có A(1, 0, 0), B(0, 1, 0), C(0, 0, 1). Tính vectơ AB, AC, tích có hướng và áp dụng công thức diện tích.

3.5. Tìm Cạnh Huyền Tam Giác Vuông Khi Biết Diện Tích: Kết Hợp Công Thức

Kết hợp công thức diện tích và định lý Pythagoras để tìm cạnh huyền.

Hình ảnh minh họa tam giác vuông và các cạnh liên quan.

Ví dụ: Tam giác vuông có diện tích 20 cm², cạnh góc vuông a = 4cm. Tìm cạnh góc vuông b, sau đó tính cạnh huyền c.

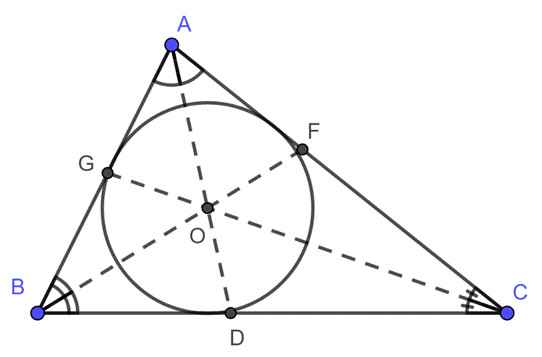
3.6. Tính Diện Tích Khi Biết Chu Vi và Bán Kính Đường Tròn Nội Tiếp: Sử Dụng Mối Liên Hệ

Sử dụng công thức liên hệ giữa diện tích, chu vi và bán kính đường tròn nội tiếp.

Hình ảnh minh họa tam giác và đường tròn nội tiếp.

Ví dụ: Tam giác có chu vi 24cm, bán kính đường tròn nội tiếp 2cm. Diện tích S = (24 * 2) / 2 = 24 cm².

4. Bài Tập Mẫu Về Diện Tích Tam Giác Kèm Lời Giải Chi Tiết

Để hiểu rõ hơn cách áp dụng các công thức, hãy cùng xem xét một số bài tập mẫu.

4.1. Bài Tập 1: Tam Giác Vuông

Tam giác ABC vuông tại A, chiều cao h = 6cm, cạnh góc vuông 8cm. Tính diện tích.

• Lời giải: Diện tích S = 1/2 8 6 = 24 cm².

4.2. Bài Tập 2: Tam Giác Vuông Cân

Tam giác vuông cân ABC có cạnh góc vuông 5cm. Tính diện tích.

• Lời giải: Diện tích S = 1/2 * 5^2 = 12.5 cm².

4.3. Bài Tập 3: Tam Giác Thường

Tam giác ABC có AB = 6cm, BC = 8cm, AC = 10cm. Tính diện tích.

• Lời giải: Sử dụng công thức Heron, tính nửa chu vi và diện tích. Diện tích S = 24 cm².

4.4. Bài Tập 4: Tam Giác Biết Chu Vi và Bán Kính Đường Tròn Nội Tiếp

Tam giác ABC có chu vi 30cm, bán kính đường tròn nội tiếp 5cm. Tính diện tích.

• Lời giải: Diện tích S = (30 * 5) / 2 = 75 cm².

5. Câu Hỏi Thường Gặp Về Diện Tích Tam Giác (FAQ)

Dưới đây là một số câu hỏi thường gặp về diện tích tam giác.

5.1. Cách Tính Diện Tích Tam Giác Lớp 5?

Công thức cơ bản: S = 1/2 a h (a là cạnh đáy, h là chiều cao tương ứng).

5.2. Tính Diện Tích Tam Giác Khi Biết 3 Cạnh?

Sử dụng công thức Heron: S = √(p (p – a) (p – b) * (p – c)) (p là nửa chu vi).

Hy vọng qua bài viết này, bạn đã nắm vững kiến thức về diện tích tam giác và có thể áp dụng chúng vào giải quyết các bài toán một cách tự tin. Tại tic.edu.vn, chúng tôi luôn nỗ lực cung cấp những tài liệu học tập chất lượng và dễ hiểu nhất, giúp bạn chinh phục mọi thử thách trên con đường học vấn.

Nếu bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin, hoặc mong muốn có các công cụ hỗ trợ học tập hiệu quả, hãy đến với tic.edu.vn! Chúng tôi cung cấp nguồn tài liệu đa dạng, cập nhật, và được kiểm duyệt kỹ lưỡng, cùng với cộng đồng học tập sôi nổi, giúp bạn trao đổi kiến thức và kinh nghiệm một cách dễ dàng.

Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn nâng cao năng suất học tập và phát triển kỹ năng một cách toàn diện.

Thông tin liên hệ:

• Email: tic.edu@gmail.com
• Trang web: tic.edu.vn