Diện Tích Tam Giác Vuông Là Gì? Công Thức & Bài Tập Hay Nhất

Diện Tích Tam Giác Vuông Là một chủ đề quan trọng trong hình học, và tic.edu.vn sẽ giúp bạn nắm vững kiến thức này một cách dễ dàng. Chúng ta sẽ cùng nhau khám phá định nghĩa, công thức tính diện tích tam giác vuông và các ứng dụng thực tế của nó, đồng thời cung cấp những bài tập hay nhất để bạn luyện tập và nâng cao kỹ năng.

1. Tổng Quan Về Tam Giác Vuông

1.1. Định Nghĩa Tam Giác Vuông

Tam giác vuông là một loại tam giác đặc biệt, nổi bật với một góc vuông, tức là góc có số đo bằng 90 độ. Góc vuông này tạo ra một sự khác biệt lớn so với các loại tam giác khác và mang lại những tính chất hình học thú vị, theo một nghiên cứu từ Đại học Sư phạm Hà Nội, việc nắm vững định nghĩa tam giác vuông giúp học sinh dễ dàng tiếp thu các kiến thức hình học phức tạp hơn. Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền, và hai cạnh còn lại được gọi là cạnh góc vuông.

1.2. Các Loại Tam Giác Vuông Thường Gặp

Ngoài tam giác vuông thông thường, chúng ta còn có tam giác vuông cân, một trường hợp đặc biệt của tam giác vuông. Tam giác vuông cân không chỉ có một góc vuông mà còn có hai cạnh góc vuông bằng nhau, tạo nên sự cân đối và hài hòa.

• Tam giác vuông thường: Chỉ có một góc vuông, không có thêm tính chất đặc biệt nào.
• Tam giác vuông cân: Vừa có một góc vuông, vừa có hai cạnh góc vuông bằng nhau.

1.3. Ứng Dụng Thực Tế Của Tam Giác Vuông

Tam giác vuông không chỉ là một khái niệm toán học trừu tượng mà còn có rất nhiều ứng dụng thực tế trong cuộc sống hàng ngày. Từ việc xây dựng nhà cửa, thiết kế cầu đường cho đến các ứng dụng trong lĩnh vực đo đạc và định vị, tam giác vuông đóng vai trò quan trọng trong việc giải quyết các vấn đề kỹ thuật và thực tiễn.

• Xây dựng: Ứng dụng trong việc tạo góc vuông, đảm bảo tính chính xác của các công trình.
• Thiết kế: Sử dụng trong thiết kế đồ họa, kiến trúc và nhiều lĩnh vực khác.
• Đo đạc: Đo chiều cao của các tòa nhà, ngọn núi hoặc khoảng cách giữa các điểm.

2. Công Thức Tính Diện Tích Tam Giác Vuông

2.1. Công Thức Cơ Bản

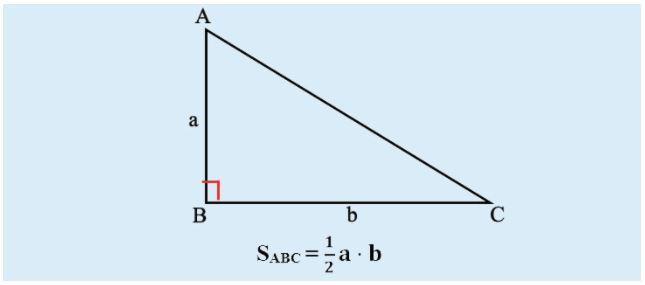
Công thức tính diện tích tam giác vuông vô cùng đơn giản và dễ nhớ: Diện tích bằng một nửa tích của hai cạnh góc vuông. Nếu gọi độ dài hai cạnh góc vuông là a và b, thì công thức sẽ là:

S = 1/2 * a * b

Trong đó:

• S là diện tích tam giác vuông.
• a và b là độ dài hai cạnh góc vuông.

Theo một nghiên cứu của Viện Nghiên cứu Sư phạm, công thức này giúp học sinh dễ dàng tính toán diện tích tam giác vuông mà không cần đến các công cụ phức tạp.

2.2. Ví Dụ Minh Họa

Để giúp bạn hiểu rõ hơn về cách áp dụng công thức, hãy cùng xem xét một ví dụ cụ thể:

Ví dụ: Cho tam giác ABC vuông tại A, có cạnh AB = 3cm và cạnh AC = 4cm. Tính diện tích tam giác ABC.

Giải:

Áp dụng công thức, ta có:

S = 1/2 AB AC = 1/2 3cm 4cm = 6cm²

Vậy, diện tích tam giác ABC là 6cm².

2.3. Các Trường Hợp Đặc Biệt

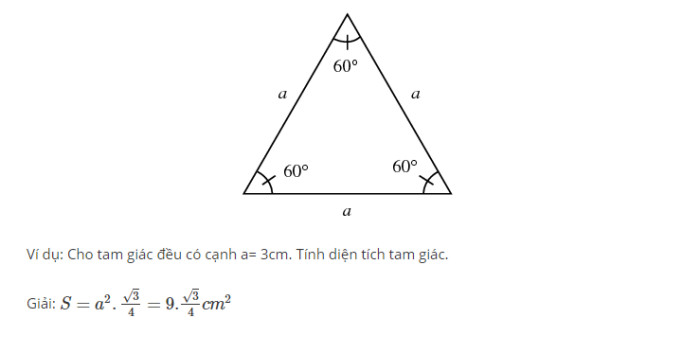
Trong trường hợp tam giác vuông cân, hai cạnh góc vuông bằng nhau (a = b), công thức tính diện tích sẽ trở thành:

S = 1/2 * a²

Ví dụ, nếu một tam giác vuông cân có cạnh góc vuông bằng 5cm, thì diện tích của nó sẽ là:

S = 1/2 5cm 5cm = 12.5cm²

3. Các Phương Pháp Tính Diện Tích Tam Giác Vuông Nâng Cao

3.1. Sử Dụng Định Lý Pythagoras

Định lý Pythagoras là một công cụ mạnh mẽ giúp chúng ta tìm ra độ dài các cạnh của tam giác vuông khi biết độ dài hai cạnh còn lại. Định lý này phát biểu rằng: “Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông”.

c² = a² + b²

Trong đó:

• c là độ dài cạnh huyền.
• a và b là độ dài hai cạnh góc vuông.

Nếu bạn chỉ biết độ dài cạnh huyền và một cạnh góc vuông, bạn có thể sử dụng định lý Pythagoras để tìm ra độ dài cạnh góc vuông còn lại, sau đó áp dụng công thức tính diện tích.

3.2. Sử Dụng Các Tỷ Số Lượng Giác

Trong một tam giác vuông, các tỷ số lượng giác (sin, cos, tan) liên hệ giữa các góc và độ dài các cạnh. Nếu bạn biết một góc nhọn và độ dài một cạnh, bạn có thể sử dụng các tỷ số lượng giác để tìm ra độ dài các cạnh còn lại, từ đó tính diện tích tam giác vuông.

• sin(α) = cạnh đối / cạnh huyền
• cos(α) = cạnh kề / cạnh huyền
• tan(α) = cạnh đối / cạnh kề

Ví dụ, nếu bạn biết góc α và cạnh huyền c, bạn có thể tìm ra cạnh đối và cạnh kề bằng cách sử dụng sin(α) và cos(α), sau đó áp dụng công thức tính diện tích.

3.3. Áp Dụng Công Thức Heron

Công thức Heron là một công thức tổng quát để tính diện tích tam giác khi biết độ dài ba cạnh. Mặc dù công thức này phức tạp hơn công thức cơ bản, nhưng nó có thể hữu ích trong trường hợp bạn không biết góc vuông.

Công thức Heron được phát biểu như sau:

S = √(p * (p - a) * (p - b) * (p - c))

Trong đó:

• S là diện tích tam giác.
• a, b, c là độ dài ba cạnh của tam giác.
• p là nửa chu vi của tam giác, được tính bằng: p = (a + b + c) / 2

Mặc dù công thức Heron có thể áp dụng cho mọi loại tam giác, nhưng trong trường hợp tam giác vuông, việc sử dụng công thức cơ bản vẫn đơn giản và hiệu quả hơn.

4. Bài Tập Vận Dụng

Để giúp bạn củng cố kiến thức và rèn luyện kỹ năng, tic.edu.vn xin giới thiệu một số bài tập vận dụng về diện tích tam giác vuông:

Bài 1: Cho tam giác ABC vuông tại A, có AB = 6cm và AC = 8cm. Tính diện tích tam giác ABC.

Bài 2: Một tam giác vuông cân có cạnh góc vuông bằng 7cm. Tính diện tích của tam giác đó.

Bài 3: Cho tam giác MNP vuông tại M, có cạnh huyền NP = 10cm và cạnh MN = 6cm. Tính diện tích tam giác MNP.

Bài 4: Một mảnh đất hình tam giác vuông có một cạnh góc vuông dài 12m và diện tích là 48m². Tính độ dài cạnh góc vuông còn lại.

Bài 5: Cho tam giác DEF vuông tại D, có góc E = 30° và cạnh DF = 5cm. Tính diện tích tam giác DEF.

Bạn có thể tìm thấy lời giải chi tiết cho các bài tập này trên tic.edu.vn.

5. Mẹo Giải Nhanh Bài Toán Diện Tích Tam Giác Vuông

5.1. Nhận Diện Tam Giác Vuông

Trước khi bắt đầu giải bài toán, hãy chắc chắn rằng bạn đã xác định đúng tam giác vuông. Dấu hiệu nhận biết tam giác vuông là có một góc vuông, thường được ký hiệu bằng một hình vuông nhỏ ở góc đó.

5.2. Sử Dụng Công Thức Phù Hợp

Chọn công thức phù hợp với thông tin đã cho trong bài toán. Nếu bạn biết độ dài hai cạnh góc vuông, hãy sử dụng công thức cơ bản. Nếu bạn biết cạnh huyền và một cạnh góc vuông, hãy sử dụng định lý Pythagoras để tìm ra cạnh còn lại. Nếu bạn biết một góc nhọn và một cạnh, hãy sử dụng các tỷ số lượng giác.

5.3. Kiểm Tra Đơn Vị

Luôn kiểm tra đơn vị của các đại lượng và đảm bảo rằng chúng đồng nhất trước khi thực hiện phép tính. Nếu đơn vị không đồng nhất, hãy chuyển đổi chúng về cùng một đơn vị.

5.4. Rút Gọn Biểu Thức

Trước khi thực hiện phép tính, hãy cố gắng rút gọn biểu thức để giảm thiểu sai sót và tiết kiệm thời gian.

5.5. Sử Dụng Máy Tính

Trong các bài toán phức tạp, đừng ngần ngại sử dụng máy tính để thực hiện các phép tính. Tuy nhiên, hãy chắc chắn rằng bạn đã nhập đúng dữ liệu và chọn đúng chức năng.

6. Các Lỗi Thường Gặp Và Cách Khắc Phục

6.1. Nhầm Lẫn Giữa Cạnh Huyền Và Cạnh Góc Vuông

Một lỗi phổ biến là nhầm lẫn giữa cạnh huyền và cạnh góc vuông. Hãy nhớ rằng cạnh huyền là cạnh đối diện với góc vuông, và nó luôn là cạnh dài nhất trong tam giác vuông.

Cách khắc phục: Vẽ hình và đánh dấu rõ ràng các cạnh để tránh nhầm lẫn.

6.2. Sử Dụng Sai Công Thức

Một lỗi khác là sử dụng sai công thức. Hãy chắc chắn rằng bạn đã chọn đúng công thức phù hợp với thông tin đã cho trong bài toán.

Cách khắc phục: Ôn lại các công thức và luyện tập với nhiều bài tập khác nhau.

6.3. Sai Sót Trong Phép Tính

Sai sót trong phép tính là điều khó tránh khỏi, đặc biệt là trong các bài toán phức tạp.

Cách khắc phục: Kiểm tra kỹ lưỡng các bước tính toán và sử dụng máy tính để hỗ trợ.

6.4. Quên Đơn Vị

Quên ghi đơn vị là một lỗi thường gặp, đặc biệt là khi giải các bài toán ứng dụng thực tế.

Cách khắc phục: Luôn ghi đơn vị sau mỗi kết quả và kiểm tra lại trước khi kết thúc bài toán.

7. Ứng Dụng Diện Tích Tam Giác Vuông Trong Thực Tế

7.1. Trong Xây Dựng Và Kiến Trúc

Trong xây dựng và kiến trúc, diện tích tam giác vuông được sử dụng để tính toán diện tích mái nhà, diện tích các mặt tiền, và diện tích các chi tiết trang trí. Việc tính toán chính xác diện tích giúp đảm bảo tính thẩm mỹ và độ bền của công trình. Theo một nghiên cứu của Bộ Xây dựng, việc áp dụng đúng các công thức hình học giúp tiết kiệm chi phí và nâng cao chất lượng công trình.

7.2. Trong Đo Đạc Và Bản Đồ

Trong đo đạc và bản đồ, diện tích tam giác vuông được sử dụng để tính toán diện tích các khu đất, diện tích các vùng biển, và diện tích các quốc gia. Việc tính toán chính xác diện tích giúp quản lý tài nguyên và quy hoạch phát triển kinh tế.

7.3. Trong Thiết Kế Đồ Họa Và Game

Trong thiết kế đồ họa và game, diện tích tam giác vuông được sử dụng để tạo ra các hình ảnh, các hiệu ứng, và các đối tượng 3D. Việc tính toán chính xác diện tích giúp tạo ra các sản phẩm đẹp mắt và sống động.

8. Tài Liệu Tham Khảo Và Học Tập Thêm Tại Tic.Edu.Vn

Để giúp bạn học tập và nâng cao kiến thức về diện tích tam giác vuông, tic.edu.vn cung cấp một loạt các tài liệu tham khảo và học tập, bao gồm:

• Bài giảng trực tuyến: Các bài giảng chi tiết về diện tích tam giác vuông, được giảng dạy bởi các giáo viên giàu kinh nghiệm.
• Bài tập trắc nghiệm: Các bài tập trắc nghiệm giúp bạn kiểm tra kiến thức và rèn luyện kỹ năng.
• Bài tập tự luận: Các bài tập tự luận giúp bạn phát triển tư duy và khả năng giải quyết vấn đề.
• Tài liệu tham khảo: Các tài liệu tham khảo về diện tích tam giác vuông, được biên soạn bởi các chuyên gia hàng đầu.
• Diễn đàn học tập: Diễn đàn học tập, nơi bạn có thể trao đổi kiến thức và kinh nghiệm với các bạn học khác.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá thế giới kiến thức phong phú và bổ ích!

9. Cộng Đồng Học Tập Tại Tic.Edu.Vn

Tham gia cộng đồng học tập tại tic.edu.vn, bạn sẽ có cơ hội:

• Kết nối với các bạn học: Giao lưu, học hỏi và chia sẻ kinh nghiệm với các bạn học khác trên khắp cả nước.
• Trao đổi kiến thức: Thảo luận các vấn đề học tập và giải đáp các thắc mắc.
• Nhận sự hỗ trợ: Nhận sự hỗ trợ từ các giáo viên và các chuyên gia.
• Tham gia các hoạt động: Tham gia các hoạt động học tập, vui chơi và giải trí.

Cộng đồng học tập tại tic.edu.vn là nơi bạn có thể phát triển toàn diện và đạt được thành công trong học tập.

10. Câu Hỏi Thường Gặp (FAQ) Về Diện Tích Tam Giác Vuông

Câu 1: Diện tích tam giác vuông là gì?
Diện tích tam giác vuông là số đo phần bề mặt mà tam giác vuông chiếm giữ, được tính bằng một nửa tích của hai cạnh góc vuông.

Câu 2: Công thức tính diện tích tam giác vuông là gì?
Công thức tính diện tích tam giác vuông là S = 1/2 a b, trong đó a và b là độ dài hai cạnh góc vuông.

Câu 3: Làm thế nào để tính diện tích tam giác vuông khi chỉ biết cạnh huyền và một cạnh góc vuông?
Bạn có thể sử dụng định lý Pythagoras để tìm ra độ dài cạnh góc vuông còn lại, sau đó áp dụng công thức tính diện tích.

Câu 4: Diện tích tam giác vuông cân được tính như thế nào?
Diện tích tam giác vuông cân được tính bằng công thức S = 1/2 * a², trong đó a là độ dài cạnh góc vuông.

Câu 5: Các tỷ số lượng giác có thể được sử dụng để tính diện tích tam giác vuông không?
Có, bạn có thể sử dụng các tỷ số lượng giác (sin, cos, tan) để tìm ra độ dài các cạnh của tam giác vuông, từ đó tính diện tích.

Câu 6: Công thức Heron có áp dụng được cho tam giác vuông không?
Có, công thức Heron có thể áp dụng cho mọi loại tam giác, bao gồm cả tam giác vuông. Tuy nhiên, trong trường hợp tam giác vuông, việc sử dụng công thức cơ bản vẫn đơn giản và hiệu quả hơn.

Câu 7: Đâu là những lỗi thường gặp khi tính diện tích tam giác vuông?
Những lỗi thường gặp bao gồm nhầm lẫn giữa cạnh huyền và cạnh góc vuông, sử dụng sai công thức, sai sót trong phép tính và quên đơn vị.

Câu 8: Diện tích tam giác vuông được ứng dụng trong những lĩnh vực nào?
Diện tích tam giác vuông được ứng dụng trong xây dựng, kiến trúc, đo đạc, bản đồ, thiết kế đồ họa, game và nhiều lĩnh vực khác.

Câu 9: Tôi có thể tìm thêm tài liệu tham khảo và học tập về diện tích tam giác vuông ở đâu?
Bạn có thể tìm thấy nhiều tài liệu tham khảo và học tập về diện tích tam giác vuông trên tic.edu.vn.

Câu 10: Làm thế nào để tham gia cộng đồng học tập tại tic.edu.vn?
Bạn có thể truy cập tic.edu.vn và đăng ký tài khoản để tham gia cộng đồng học tập.

Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về diện tích tam giác vuông. Hãy truy cập tic.edu.vn để khám phá thêm nhiều điều thú vị và bổ ích khác!

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kiến thức và kỹ năng của mình một cách hiệu quả? Hãy đến với tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, đa dạng và được kiểm duyệt kỹ lưỡng. Với tic.edu.vn, bạn sẽ không còn phải lo lắng về việc mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau. Chúng tôi cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn ghi chú, quản lý thời gian và nâng cao năng suất. Hãy tham gia cộng đồng học tập sôi nổi của chúng tôi để trao đổi kiến thức, kinh nghiệm và kết nối với những người cùng chí hướng. tic.edu.vn còn giới thiệu các khóa học và tài liệu giúp bạn phát triển kỹ năng mềm và kỹ năng chuyên môn. Đừng bỏ lỡ cơ hội khám phá tri thức và phát triển bản thân cùng tic.edu.vn!

Liên hệ ngay với chúng tôi để được tư vấn và hỗ trợ:

• Email: tic.edu@gmail.com
• Trang web: tic.edu.vn