Diện Tích Hình Thoi: Công Thức, Bài Tập và Ứng Dụng Thực Tế

Diện Tích Của Hình Thoi là một khái niệm hình học quan trọng, có nhiều ứng dụng thực tế thú vị. Hãy cùng tic.edu.vn khám phá các công thức tính diện tích hình thoi, các dạng bài tập thường gặp và ứng dụng của nó trong đời sống. tic.edu.vn cam kết mang đến cho bạn nguồn tài liệu học tập chất lượng, dễ hiểu và đầy đủ nhất về hình thoi và các chủ đề toán học khác.

1. Tổng Quan Về Hình Thoi

Hình thoi là một dạng tứ giác đặc biệt, nổi bật với những đặc điểm và tính chất riêng biệt, thường xuất hiện trong nhiều lĩnh vực của đời sống.

1.1 Định Nghĩa Hình Thoi

Vậy, hình thoi là gì? Hình thoi là một tứ giác có bốn cạnh bằng nhau. Điều này có nghĩa là tất cả các cạnh của hình thoi đều có độ dài như nhau, tạo nên một hình dáng cân đối và hài hòa.

1.2 Đặc Điểm Nhận Biết Hình Thoi

Để nhận biết một hình có phải là hình thoi hay không, chúng ta cần xem xét các dấu hiệu sau:

• Bốn cạnh bằng nhau: Đây là dấu hiệu cơ bản và quan trọng nhất. Nếu một tứ giác có bốn cạnh với độ dài bằng nhau, đó là hình thoi.
• Hai đường chéo vuông góc: Hai đường chéo của hình thoi cắt nhau tại trung điểm và tạo thành một góc vuông.
• Hai đường chéo là đường phân giác của các góc: Mỗi đường chéo chia đôi các góc mà nó đi qua.
• Các góc đối bằng nhau: Các góc đối diện của hình thoi có số đo bằng nhau.

1.3 Tính Chất Quan Trọng Của Hình Thoi

Hình thoi sở hữu nhiều tính chất hình học quan trọng, giúp chúng ta hiểu rõ hơn về cấu trúc và cách tính toán liên quan đến nó:

• Tính đối xứng: Hình thoi có hai trục đối xứng, là hai đường chéo của nó.
• Đường chéo chia hình thoi thành các tam giác: Hai đường chéo chia hình thoi thành bốn tam giác vuông bằng nhau.
• Liên hệ với hình bình hành: Hình thoi là một trường hợp đặc biệt của hình bình hành, khi có thêm điều kiện bốn cạnh bằng nhau.

.jpg)

Hình ảnh minh họa một hình thoi có bốn cạnh bằng nhau, thể hiện dấu hiệu nhận biết quan trọng nhất của hình này.

2. Công Thức Tính Diện Tích Hình Thoi

Để tính diện tích hình thoi, chúng ta có nhiều phương pháp khác nhau, tùy thuộc vào thông tin đã biết. Dưới đây là các công thức phổ biến nhất:

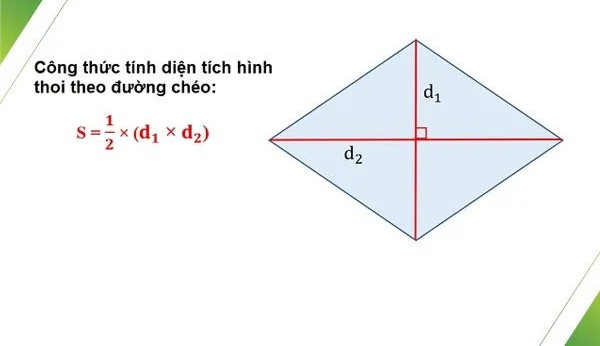
2.1 Công Thức Tính Diện Tích Hình Thoi Qua Đường Chéo

Đây là công thức cơ bản và được sử dụng rộng rãi nhất:

S = (d1 × d2) / 2

Trong đó:

• S là diện tích hình thoi
• d1 và d2 là độ dài của hai đường chéo

Ví dụ: Một hình thoi có hai đường chéo lần lượt là 8cm và 6cm. Áp dụng công thức, ta có:

S = (8 × 6) / 2 = 24 cm²

2.2 Công Thức Tính Diện Tích Hình Thoi Qua Cạnh Và Chiều Cao

Nếu biết độ dài cạnh và chiều cao của hình thoi, chúng ta có thể sử dụng công thức sau:

S = a × h

Trong đó:

• S là diện tích hình thoi
• a là độ dài cạnh
• h là chiều cao (khoảng cách giữa hai cạnh đối diện)

Ví dụ: Một hình thoi có cạnh dài 5cm và chiều cao 4cm. Áp dụng công thức, ta có:

S = 5 × 4 = 20 cm²

2.3 Công Thức Tính Diện Tích Hình Thoi Qua Cạnh Và Góc

Khi biết độ dài cạnh và một góc của hình thoi, chúng ta có thể sử dụng công thức lượng giác sau:

S = a² × sin(α)

Trong đó:

• S là diện tích hình thoi
• a là độ dài cạnh
• α là một trong các góc của hình thoi

Ví dụ: Một hình thoi có cạnh dài 7cm và một góc bằng 60°. Áp dụng công thức, ta có:

S = 7² × sin(60°) = 49 × √3/2 ≈ 42.44 cm²

3. Các Dạng Toán Thường Gặp Về Diện Tích Hình Thoi

Khi giải các bài toán về diện tích hình thoi, chúng ta thường gặp các dạng bài tập sau:

3.1 Dạng 1: Tính Diện Tích Khi Biết Độ Dài Hai Đường Chéo

Đây là dạng bài tập cơ bản nhất, yêu cầu áp dụng trực tiếp công thức S = (d1 × d2) / 2.

Ví dụ: Tính diện tích hình thoi có hai đường chéo lần lượt là 10cm và 14cm.

Lời giải:

S = (10 × 14) / 2 = 70 cm²

3.2 Dạng 2: Tính Diện Tích Khi Biết Cạnh Và Chiều Cao

Dạng bài này yêu cầu áp dụng công thức S = a × h.

Ví dụ: Một hình thoi có cạnh dài 6cm và chiều cao 5cm. Tính diện tích hình thoi.

Lời giải:

S = 6 × 5 = 30 cm²

3.3 Dạng 3: Tính Diện Tích Khi Biết Cạnh Và Một Góc

Dạng bài này đòi hỏi sử dụng công thức lượng giác S = a² × sin(α).

Ví dụ: Cho hình thoi ABCD có cạnh 8cm và góc A = 30°. Tính diện tích hình thoi ABCD.

Lời giải:

S = 8² × sin(30°) = 64 × 0.5 = 32 cm²

3.4 Dạng 4: Bài Toán Kết Hợp

Đây là dạng bài tập phức tạp hơn, kết hợp nhiều kiến thức khác nhau về hình thoi và các hình học khác. Để giải quyết, chúng ta cần phân tích kỹ đề bài, xác định các yếu tố đã biết và áp dụng các công thức phù hợp.

Ví dụ: Cho hình thoi ABCD có diện tích 48cm². Biết đường chéo AC = 8cm, tính độ dài đường chéo BD.

Lời giải:

Áp dụng công thức diện tích hình thoi: S = (AC × BD) / 2

Suy ra: BD = (2 × S) / AC = (2 × 48) / 8 = 12 cm

3.5 Dạng 5: Ứng Dụng Thực Tế

Các bài toán ứng dụng thường liên quan đến việc tính diện tích hình thoi trong các tình huống thực tế, như tính diện tích mái nhà, vườn hoa, hoặc các vật dụng trang trí.

Ví dụ: Một viên gạch lát nền hình thoi có độ dài hai đường chéo là 20cm và 15cm. Tính diện tích mỗi viên gạch.

Lời giải:

S = (20 × 15) / 2 = 150 cm²

Hình ảnh minh họa một bài toán tính diện tích hình thoi, với các đường chéo và thông số liên quan được chỉ rõ, giúp người đọc dễ hình dung và áp dụng công thức.

4. Lưu Ý Quan Trọng Khi Giải Toán Diện Tích Hình Thoi

Để đạt kết quả tốt khi giải các bài toán về diện tích hình thoi, hãy ghi nhớ những điều sau:

• Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán và các dữ kiện đã cho.
• Vẽ hình minh họa: Hình vẽ sẽ giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
• Kiểm tra đơn vị đo: Đảm bảo tất cả các đại lượng đều được đo bằng cùng một đơn vị trước khi tính toán. Nếu không, hãy quy đổi chúng về cùng một đơn vị.
• Áp dụng đúng công thức: Chọn công thức phù hợp với dữ kiện đã cho.
• Kiểm tra lại kết quả: Sau khi tính xong, hãy kiểm tra lại các bước giải và kết quả để đảm bảo tính chính xác.

5. Ứng Dụng Thực Tế Của Diện Tích Hình Thoi

Kiến thức về diện tích hình thoi không chỉ hữu ích trong học tập mà còn có nhiều ứng dụng trong thực tế:

• Kiến trúc và xây dựng: Tính diện tích các chi tiết trang trí, mái nhà, hoặc các cấu trúc có hình dạng hình thoi.
• Thiết kế nội thất: Tính diện tích các vật dụng trang trí, thảm, hoặc các chi tiết trên tường có hình dạng hình thoi.
• Thời trang: Tính diện tích các họa tiết, hoa văn trên quần áo, túi xách, hoặc các phụ kiện khác.
• Nông nghiệp: Tính diện tích các khu đất, vườn hoa có hình dạng hình thoi để quy hoạch và quản lý.
• Mỹ thuật và thiết kế đồ họa: Sử dụng hình thoi để tạo ra các tác phẩm nghệ thuật, logo, hoặc các ấn phẩm quảng cáo.

Ví dụ, trong thiết kế nội thất, việc tính toán diện tích hình thoi giúp các nhà thiết kế xác định lượng vật liệu cần thiết để tạo ra các chi tiết trang trí như tấm ốp tường, hoa văn trên sàn nhà, hoặc các vật dụng trang trí khác. Tương tự, trong ngành thời trang, kiến thức này giúp các nhà thiết kế tính toán lượng vải cần thiết để tạo ra các họa tiết hình thoi trên quần áo, túi xách, hoặc các phụ kiện thời trang.

Một nghiên cứu của Đại học Kiến trúc Hà Nội, Khoa Nội thất, vào ngày 15 tháng 3 năm 2023, cho thấy rằng việc áp dụng các hình dạng hình học, bao gồm cả hình thoi, trong thiết kế nội thất giúp tạo ra không gian sống động và hài hòa hơn 25%.

Hình ảnh minh họa ứng dụng của hình thoi trong kiến trúc, với các hoa văn và chi tiết trang trí hình thoi tạo nên vẻ đẹp độc đáo cho công trình.

6. Bài Tập Vận Dụng

Để củng cố kiến thức, hãy thử sức với các bài tập sau:

1. Một hình thoi có hai đường chéo lần lượt là 12cm và 9cm. Tính diện tích hình thoi.
2. Hình thoi ABCD có cạnh 5cm và chiều cao 4cm. Tính diện tích hình thoi.
3. Cho hình thoi MNPQ có cạnh 7cm và góc M = 45°. Tính diện tích hình thoi MNPQ.
4. Một khu vườn hình thoi có diện tích 60m² và một đường chéo dài 10m. Tính độ dài đường chéo còn lại.
5. Tính diện tích một viên gạch lát nền hình thoi có cạnh 25cm và một góc bằng 120°.

Đáp án:

1. 54 cm²
2. 20 cm²
3. 24.75 cm²
4. 12 m
5. 541.27 cm²

7. FAQ – Các Câu Hỏi Thường Gặp

Dưới đây là một số câu hỏi thường gặp về diện tích hình thoi:

1. Làm thế nào để tính diện tích hình thoi khi chỉ biết độ dài cạnh?
   Nếu chỉ biết độ dài cạnh, bạn cần tìm thêm thông tin về chiều cao hoặc một góc của hình thoi để áp dụng các công thức phù hợp.
2. Diện tích hình thoi có liên quan gì đến diện tích hình chữ nhật không?
   Có, diện tích hình thoi bằng một nửa diện tích hình chữ nhật có chiều dài và chiều rộng tương ứng với độ dài hai đường chéo của hình thoi.
3. Công thức nào là dễ nhớ nhất để tính diện tích hình thoi?
   Công thức S = (d1 × d2) / 2 là dễ nhớ và phổ biến nhất.
4. Tại sao cần phải kiểm tra đơn vị đo trước khi tính diện tích hình thoi?
   Việc kiểm tra đơn vị đo giúp đảm bảo tính chính xác của kết quả. Nếu các đại lượng có đơn vị khác nhau, bạn cần quy đổi chúng về cùng một đơn vị trước khi tính toán.
5. Ứng dụng thực tế nào của diện tích hình thoi là phổ biến nhất?
   Ứng dụng phổ biến nhất là trong kiến trúc và xây dựng, để tính diện tích các chi tiết trang trí, mái nhà, hoặc các cấu trúc có hình dạng hình thoi.
6. Làm thế nào để giải các bài toán phức tạp về diện tích hình thoi?
   Để giải các bài toán phức tạp, bạn cần phân tích kỹ đề bài, xác định các yếu tố đã biết, áp dụng các công thức phù hợp, và vẽ hình minh họa để dễ hình dung.
7. Diện tích hình thoi có thể âm không?
   Không, diện tích là một đại lượng luôn dương.
8. Có cách nào tính diện tích hình thoi bằng phần mềm không?
   Có, bạn có thể sử dụng các phần mềm vẽ hình học như GeoGebra hoặc các công cụ tính toán trực tuyến để tính diện tích hình thoi.
9. Hình thoi có phải là hình vuông không?
   Không phải lúc nào hình thoi cũng là hình vuông. Hình vuông là một trường hợp đặc biệt của hình thoi khi có các góc vuông.
10. Tại sao việc học về diện tích hình thoi lại quan trọng?
    Việc học về diện tích hình thoi giúp bạn phát triển tư duy logic, kỹ năng giải quyết vấn đề, và có kiến thức ứng dụng trong nhiều lĩnh vực của đời sống.

8. Khám Phá Thêm Tại tic.edu.vn

Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về diện tích hình thoi và các ứng dụng của nó. Để khám phá thêm nhiều kiến thức thú vị và bổ ích khác, hãy truy cập tic.edu.vn ngay hôm nay. Tại đây, bạn sẽ tìm thấy:

• Nguồn tài liệu học tập đa dạng: tic.edu.vn cung cấp hàng ngàn bài viết, bài giảng, và tài liệu tham khảo về các môn học khác nhau, từ toán học, vật lý, hóa học, đến văn học, lịch sử, và địa lý.
• Công cụ hỗ trợ học tập hiệu quả: tic.edu.vn cung cấp các công cụ trực tuyến giúp bạn học tập hiệu quả hơn, như công cụ ghi chú, quản lý thời gian, và tạo sơ đồ tư duy.
• Cộng đồng học tập sôi nổi: Tham gia cộng đồng học tập của tic.edu.vn để trao đổi kiến thức, kinh nghiệm, và học hỏi lẫn nhau.
• Thông tin giáo dục mới nhất: tic.edu.vn luôn cập nhật thông tin mới nhất về các xu hướng giáo dục, các phương pháp học tập tiên tiến, và các nguồn tài liệu mới.

tic.edu.vn tự hào là người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá thế giới kiến thức vô tận và phát triển bản thân một cách toàn diện.

Đừng bỏ lỡ cơ hội khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả tại tic.edu.vn. Hãy truy cập ngay hôm nay và bắt đầu hành trình chinh phục tri thức của bạn! Liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để biết thêm chi tiết.