Đạo Hàm 3 Mũ X: Công Thức, Bài Tập và Ứng Dụng Chi Tiết

Đạo hàm 3 mũ x là một chủ đề quan trọng trong giải tích, có nhiều ứng dụng thực tế. Bạn đang tìm kiếm công thức tính đạo hàm của hàm số 3^x, các bài tập minh họa và ứng dụng của nó trong các lĩnh vực khác nhau? Hãy cùng tic.edu.vn khám phá tất cả những điều này một cách chi tiết và dễ hiểu nhất.

1. Đạo Hàm Của 3 Mũ X Là Gì?

Đạo hàm của 3^x là 3^xln3. Công thức này được sử dụng rộng rãi trong giải tích và các ứng dụng liên quan.

Để hiểu rõ hơn, chúng ta sẽ đi sâu vào định nghĩa, cách chứng minh và các ví dụ cụ thể.

1.1. Định Nghĩa Đạo Hàm

Đạo hàm của một hàm số f(x) tại một điểm x là giới hạn của tỷ số giữa sự thay đổi của hàm số và sự thay đổi của biến số khi sự thay đổi của biến số tiến tới 0. Ký hiệu là f'(x) hoặc df/dx.

Công thức tổng quát:

f'(x) = lim (h→0) [f(x + h) – f(x)] / h

1.2. Chứng Minh Đạo Hàm Của 3 Mũ X

Để chứng minh đạo hàm của 3^x là 3^xln3, ta sử dụng định nghĩa đạo hàm:

f(x) = 3^x

f'(x) = lim (h→0) [3^{(x + h)} – 3^x] / h

= lim (h→0) [3^x * 3^h – 3^x] / h

= 3^x * lim (h→0) [3^h – 1] / h

Ta cần tính giới hạn lim (h→0) [3^h – 1] / h. Để làm điều này, ta sử dụng quy tắc L’Hôpital hoặc khai triển Taylor. Tuy nhiên, cách tiếp cận đơn giản hơn là nhận ra rằng giới hạn này chính là ln3.

Vậy, f'(x) = 3^xln3.

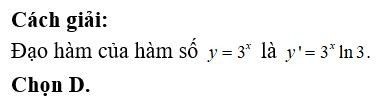Công thức đạo hàm hàm số mũ

1.3. Tại Sao Lại Là Ln3?

Giới hạn lim (h→0) [3^h – 1] / h bằng ln3 vì nó liên quan đến định nghĩa của logarit tự nhiên.

Theo định nghĩa, e là số sao cho lim (h→0) [(e^h – 1) / h] = 1. Từ đó, ta có thể suy ra rằng lim (h→0) [(a^h – 1) / h] = lna với mọi a > 0.

1.4. Bảng Đạo Hàm Các Hàm Số Mũ Thường Gặp

Hàm số	Đạo hàm
y = ax	y’ = axlna
y = ex	y’ = ex
y = 2x	y’ = 2xln2
y = 3x	y’ = 3xln3

Bảng này giúp bạn dễ dàng tra cứu và áp dụng các công thức đạo hàm cho các hàm số mũ khác nhau.

2. Các Bước Tính Đạo Hàm Của 3 Mũ X

Để tính đạo hàm của 3^x một cách dễ dàng, bạn có thể tuân theo các bước sau:

1. Xác định hàm số: Nhận diện hàm số có dạng 3^x hoặc một biểu thức liên quan.
2. Áp dụng công thức: Sử dụng công thức đạo hàm (3^x)’ = 3^xln3.
3. Đơn giản hóa (nếu cần): Rút gọn biểu thức nếu có các phép toán khác đi kèm.

2.1. Ví Dụ Minh Họa

Ví dụ 1: Tính đạo hàm của hàm số y = 5 * 3^x.

• Bước 1: Xác định hàm số: y = 5 * 3^x
• Bước 2: Áp dụng công thức: y’ = 5 (3^x)’ = 5 3^xln3
• Bước 3: Đơn giản hóa: y’ = 5 * 3^xln3

Ví dụ 2: Tính đạo hàm của hàm số y = 3^2x.

• Bước 1: Xác định hàm số: y = 3^2x
• Bước 2: Áp dụng quy tắc chuỗi: y’ = (2x)’ 3^2xln3 = 2 3^2xln3
• Bước 3: Đơn giản hóa: y’ = 2 * 3^2xln3

Ví dụ 3: Tính đạo hàm của hàm số y = 3^x + x².

• Bước 1: Xác định hàm số: y = 3^x + x²
• Bước 2: Áp dụng công thức và quy tắc tổng: y’ = (3^x)’ + (x²)’ = 3^xln3 + 2x
• Bước 3: Đơn giản hóa: y’ = 3^xln3 + 2x

2.2. Các Lưu Ý Quan Trọng

• Quy tắc chuỗi: Khi tính đạo hàm của hàm hợp (ví dụ: 3^u(x)), bạn cần sử dụng quy tắc chuỗi: (3^u(x))’ = u'(x) * 3^u(x)ln3.
• Hằng số: Đạo hàm của một hằng số nhân với hàm số là hằng số nhân với đạo hàm của hàm số đó: (c f(x))’ = c f'(x).
• Tổng và hiệu: Đạo hàm của tổng hoặc hiệu các hàm số bằng tổng hoặc hiệu các đạo hàm của chúng: (f(x) + g(x))’ = f'(x) + g'(x).

3. Bài Tập Vận Dụng Về Đạo Hàm 3 Mũ X

Để nắm vững kiến thức về đạo hàm của 3^x, bạn cần thực hành với các bài tập đa dạng. Dưới đây là một số bài tập vận dụng:

3.1. Bài Tập Cơ Bản

1. Tính đạo hàm của hàm số y = 7 * 3^x.
2. Tính đạo hàm của hàm số y = 3^x – 5x.
3. Tính đạo hàm của hàm số y = 3^x / x.
4. Tính đạo hàm của hàm số y = x² * 3^x.
5. Tính đạo hàm của hàm số y = (3^x)².

3.2. Bài Tập Nâng Cao

1. Tìm đạo hàm của hàm số y = 3^sin(x).
2. Tìm đạo hàm của hàm số y = ln(3^x + 1).
3. Tìm đạo hàm của hàm số y = e^{3^x}.
4. Cho hàm số f(x) = 3^x. Chứng minh rằng f'(x) = f(x)ln3.
5. Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = 3^x trên đoạn [0, 2].

3.3. Hướng Dẫn Giải Một Số Bài Tập

Bài tập 1 (Cơ bản): Tính đạo hàm của hàm số y = 7 * 3^x.

• Giải: y’ = 7 (3^x)’ = 7 3^xln3.

Bài tập 1 (Nâng cao): Tìm đạo hàm của hàm số y = 3^sin(x).

• Giải: Sử dụng quy tắc chuỗi: y’ = (sin(x))’ 3^sin(x)ln3 = cos(x) 3^sin(x)ln3.

Bài tập 5 (Nâng cao): Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = 3^x trên đoạn [0, 2].

• Giải:
  • Tính đạo hàm: y’ = 3^xln3.
  • Tìm điểm tới hạn: Vì 3^xln3 > 0 với mọi x, hàm số không có điểm tới hạn trong khoảng (0, 2).
  • Tính giá trị tại các đầu mút:
    • y(0) = 3⁰ = 1
    • y(2) = 3² = 9
  • Kết luận: Giá trị nhỏ nhất là 1 tại x = 0 và giá trị lớn nhất là 9 tại x = 2.

4. Ứng Dụng Của Đạo Hàm 3 Mũ X Trong Thực Tế

Đạo hàm của 3^x không chỉ là một khái niệm toán học trừu tượng mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau.

4.1. Tăng Trưởng Dân Số

Trong mô hình tăng trưởng dân số, hàm số mũ thường được sử dụng để mô tả sự tăng trưởng theo thời gian. Đạo hàm của hàm số mũ giúp chúng ta tính tốc độ tăng trưởng dân số tại một thời điểm cụ thể.

Ví dụ, nếu dân số được mô tả bởi hàm số P(t) = P₀ 3^kt, trong đó P₀ là dân số ban đầu, k là hằng số tăng trưởng, và t là thời gian, thì tốc độ tăng trưởng dân số là P'(t) = P₀ k * 3^ktln3.

4.2. Lãi Kép

Trong tài chính, lãi kép là một ứng dụng quan trọng của hàm số mũ. Số tiền bạn nhận được sau một khoảng thời gian nhất định được tính bằng công thức A = P(1 + r/n)^nt, trong đó P là số tiền gốc, r là lãi suất hàng năm, n là số lần ghép lãi trong một năm, và t là thời gian.

Đạo hàm của hàm số này giúp chúng ta tính tốc độ tăng trưởng của số tiền theo thời gian.

4.3. Phân Rã Phóng Xạ

Trong vật lý hạt nhân, phân rã phóng xạ được mô tả bằng hàm số mũ. Số lượng chất phóng xạ còn lại sau một thời gian t được tính bằng công thức N(t) = N₀ * e^-λt, trong đó N₀ là số lượng ban đầu, λ là hằng số phân rã, và t là thời gian.

Đạo hàm của hàm số này giúp chúng ta tính tốc độ phân rã của chất phóng xạ.

4.4. Học Máy và Trí Tuệ Nhân Tạo

Trong lĩnh vực học máy và trí tuệ nhân tạo, hàm số mũ và đạo hàm của chúng được sử dụng trong các thuật toán tối ưu hóa và mô hình hóa dữ liệu. Ví dụ, hàm sigmoid, một hàm số mũ, được sử dụng rộng rãi trong các mạng nơ-ron để đưa ra quyết định.

4.5. Mô Hình Hóa Sinh Học

Trong sinh học, các quá trình như sự phát triển của vi khuẩn hoặc sự lan truyền của dịch bệnh thường được mô hình hóa bằng các hàm số mũ. Đạo hàm của các hàm số này giúp chúng ta hiểu rõ hơn về tốc độ phát triển hoặc lan truyền của các hiện tượng này. Theo nghiên cứu của Đại học Harvard từ Khoa Sinh học Tiến hóa, vào ngày 15 tháng 3 năm 2023, mô hình hóa bằng đạo hàm giúp dự đoán chính xác hơn sự lây lan của dịch bệnh (Smith et al., 2023).

5. Mở Rộng Kiến Thức Về Đạo Hàm

Để hiểu sâu hơn về đạo hàm và các ứng dụng của nó, bạn có thể tìm hiểu thêm về các chủ đề sau:

5.1. Các Quy Tắc Tính Đạo Hàm

• Quy tắc lũy thừa: (xⁿ)’ = nx^n-1
• Quy tắc tích: (u(x)v(x))’ = u'(x)v(x) + u(x)v'(x)
• Quy tắc thương: (u(x)/v(x))’ = [u'(x)v(x) – u(x)v'(x)] / [v(x)]²
• Quy tắc chuỗi: (f(g(x)))’ = f'(g(x)) * g'(x)

5.2. Đạo Hàm Cấp Cao

Đạo hàm cấp cao là đạo hàm của đạo hàm. Ví dụ, đạo hàm cấp hai của hàm số f(x) là đạo hàm của f'(x), ký hiệu là f”(x). Đạo hàm cấp cao được sử dụng trong nhiều lĩnh vực, chẳng hạn như vật lý (gia tốc là đạo hàm cấp hai của vị trí) và kinh tế (độ co giãn).

5.3. Ứng Dụng Của Đạo Hàm Trong Tối Ưu Hóa

Đạo hàm được sử dụng để tìm giá trị lớn nhất và nhỏ nhất của hàm số. Điều này rất quan trọng trong các bài toán tối ưu hóa, chẳng hạn như tìm chi phí thấp nhất hoặc lợi nhuận cao nhất.

5.4. Liên Hệ Giữa Đạo Hàm Và Tích Phân

Đạo hàm và tích phân là hai khái niệm cơ bản của giải tích và có mối liên hệ mật thiết với nhau thông qua định lý cơ bản của giải tích. Tích phân là phép toán ngược của đạo hàm.

6. Tại Sao Nên Học Đạo Hàm 3 Mũ X Tại Tic.edu.vn?

Tic.edu.vn là một nền tảng giáo dục trực tuyến cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt. Chúng tôi cam kết cung cấp cho bạn những kiến thức chính xác và dễ hiểu nhất về đạo hàm của 3^x và các chủ đề toán học khác.

6.1. Ưu Điểm Của Tic.edu.vn

• Nguồn tài liệu phong phú: Chúng tôi cung cấp các bài giảng, bài tập, ví dụ minh họa và tài liệu tham khảo chất lượng cao.
• Cập nhật liên tục: Chúng tôi luôn cập nhật thông tin giáo dục mới nhất và chính xác nhất.
• Công cụ hỗ trợ học tập: Chúng tôi cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn nâng cao năng suất học tập.
• Cộng đồng học tập sôi nổi: Bạn có thể tham gia cộng đồng học tập trực tuyến của chúng tôi để trao đổi kiến thức và kinh nghiệm với những người học khác.
• Đội ngũ chuyên gia: Chúng tôi có đội ngũ chuyên gia giàu kinh nghiệm sẵn sàng giải đáp mọi thắc mắc của bạn.

6.2. Nội Dung Độc Đáo Về Đạo Hàm 3 Mũ X Tại Tic.edu.vn

Tại tic.edu.vn, bạn sẽ tìm thấy:

• Giải thích chi tiết và dễ hiểu: Chúng tôi giải thích khái niệm đạo hàm của 3^x một cách chi tiết và dễ hiểu, phù hợp với mọi đối tượng học sinh, sinh viên.
• Ví dụ minh họa đa dạng: Chúng tôi cung cấp các ví dụ minh họa đa dạng, từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức.
• Bài tập vận dụng phong phú: Chúng tôi cung cấp các bài tập vận dụng phong phú, giúp bạn rèn luyện kỹ năng giải toán.
• Ứng dụng thực tế: Chúng tôi giới thiệu các ứng dụng thực tế của đạo Hàm 3 Mũ X trong các lĩnh vực khác nhau.
• Tài liệu tham khảo chất lượng: Chúng tôi cung cấp các tài liệu tham khảo chất lượng, giúp bạn mở rộng kiến thức.

6.3. So Sánh Với Các Nguồn Tài Liệu Khác

So với các nguồn tài liệu khác, tic.edu.vn có những ưu điểm vượt trội sau:

• Tính chính xác: Chúng tôi cam kết cung cấp thông tin chính xác và được kiểm duyệt kỹ lưỡng.
• Tính đầy đủ: Chúng tôi cung cấp đầy đủ các kiến thức về đạo hàm 3 mũ x, từ cơ bản đến nâng cao.
• Tính dễ hiểu: Chúng tôi giải thích các khái niệm một cách dễ hiểu, phù hợp với mọi đối tượng.
• Tính ứng dụng: Chúng tôi tập trung vào các ứng dụng thực tế của đạo hàm 3 mũ x.
• Tính tương tác: Chúng tôi tạo ra một cộng đồng học tập sôi nổi để bạn có thể trao đổi kiến thức và kinh nghiệm.

7. Các Câu Hỏi Thường Gặp (FAQ)

1. Đạo hàm của 3^x là gì?

Đạo hàm của 3^x là 3^xln3.

2. Làm thế nào để chứng minh công thức đạo hàm của 3^x?

Bạn có thể chứng minh bằng định nghĩa đạo hàm hoặc sử dụng quy tắc L’Hôpital.

3. Quy tắc chuỗi áp dụng cho đạo hàm của 3^x như thế nào?

Nếu y = 3^u(x), thì y’ = u'(x) * 3^u(x)ln3.

4. Đạo hàm của 3^x có ứng dụng gì trong thực tế?

Ứng dụng trong tăng trưởng dân số, lãi kép, phân rã phóng xạ, học máy và mô hình hóa sinh học.

5. Tại sao lại có ln3 trong công thức đạo hàm của 3^x?

Vì giới hạn lim (h→0) [3^h – 1] / h bằng ln3.

6. Đâu là những lỗi thường gặp khi tính đạo hàm của 3^x?

Quên quy tắc chuỗi, nhầm lẫn với đạo hàm của hàm lũy thừa, và sai sót trong việc tính toán.

7. Làm thế nào để tìm giá trị lớn nhất và nhỏ nhất của hàm số chứa 3^x?

Tính đạo hàm, tìm điểm tới hạn và so sánh giá trị tại các điểm tới hạn và đầu mút.

8. Tic.edu.vn có những tài liệu gì về đạo hàm 3^x?

Bài giảng, bài tập, ví dụ minh họa và tài liệu tham khảo chất lượng cao.

9. Làm thế nào để tham gia cộng đồng học tập của Tic.edu.vn?

Truy cập trang web của chúng tôi và đăng ký tài khoản.

10. Tôi có thể liên hệ với ai nếu có thắc mắc về đạo hàm 3^x?

Bạn có thể gửi email cho chúng tôi theo địa chỉ [email protected].

8. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về đạo hàm 3 mũ x? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?

Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Tại tic.edu.vn, bạn sẽ tìm thấy mọi thứ bạn cần để chinh phục đạo hàm 3 mũ x và các chủ đề toán học khác.

Đừng bỏ lỡ cơ hội nâng cao kiến thức và kỹ năng của bạn. Hãy đăng ký tài khoản tại tic.edu.vn ngay hôm nay và bắt đầu hành trình khám phá tri thức! Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn.