**Đặc Điểm Hình Bình Hành: Định Nghĩa, Tính Chất và Ứng Dụng**

Hình bình hành là một hình tứ giác đặc biệt với nhiều ứng dụng trong toán học và đời sống. Bài viết này của tic.edu.vn sẽ cung cấp cho bạn một cái nhìn toàn diện về hình bình hành, từ định nghĩa, tính chất, dấu hiệu nhận biết đến các công thức tính toán và ứng dụng thực tế. Hãy cùng tic.edu.vn khám phá thế giới hình học thú vị này nhé!

1. Hình Bình Hành Là Gì? Định Nghĩa Chi Tiết

Hình bình hành là một loại tứ giác đặc biệt, được tạo thành từ hai cặp cạnh đối diện song song và bằng nhau. Nói một cách đơn giản, đó là một hình tứ giác có các cạnh đối diện không bao giờ cắt nhau, dù có kéo dài đến đâu đi chăng nữa. Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học vào ngày 15/03/2023, hình bình hành là một trong những hình học cơ bản quan trọng trong chương trình toán phổ thông.

1.1. So Sánh Hình Bình Hành Với Các Hình Tứ Giác Khác

Để hiểu rõ hơn về hình bình hành, chúng ta hãy so sánh nó với các hình tứ giác khác:

• Hình chữ nhật: Hình chữ nhật là một trường hợp đặc biệt của hình bình hành, có thêm điều kiện là tất cả các góc đều là góc vuông (90 độ).
• Hình vuông: Hình vuông là một trường hợp đặc biệt của cả hình chữ nhật và hình bình hành, vừa có các góc vuông, vừa có các cạnh bằng nhau.
• Hình thoi: Hình thoi là một hình bình hành có tất cả các cạnh bằng nhau.
• Hình thang: Hình thang chỉ có một cặp cạnh đối diện song song, không giống như hình bình hành có hai cặp cạnh đối diện song song.

1.2. Ứng Dụng Thực Tế Của Hình Bình Hành

Hình bình hành xuất hiện rất nhiều trong cuộc sống hàng ngày của chúng ta. Bạn có thể dễ dàng nhận thấy chúng trong:

• Kiến trúc: Nhiều công trình kiến trúc sử dụng hình bình hành trong thiết kế để tạo sự độc đáo và cân đối.
• Nội thất: Bàn ghế, tủ kệ có thể có mặt cắt hình bình hành.
• Thiết kế đồ họa: Hình bình hành được sử dụng để tạo hiệu ứng 3D, phối cảnh trong thiết kế.
• Toán học và vật lý: Hình bình hành được sử dụng để biểu diễn các vectơ và lực trong các bài toán.

2. Tính Chất Của Hình Bình Hành: Khám Phá Những Điều Thú Vị

Hình bình hành sở hữu những tính chất đặc biệt, giúp chúng ta dễ dàng nhận biết và ứng dụng vào giải toán.

2.1. Tính Chất Về Cạnh

• Các cạnh đối diện song song: Đây là tính chất quan trọng nhất, định nghĩa nên hình bình hành.
• Các cạnh đối diện bằng nhau: Nếu một tứ giác có các cạnh đối diện bằng nhau, nó là hình bình hành.

2.2. Tính Chất Về Góc

• Các góc đối diện bằng nhau: Hai góc đối diện của hình bình hành luôn có số đo bằng nhau.
• Tổng hai góc kề một cạnh bằng 180 độ: Hai góc nằm cạnh nhau trên một cạnh của hình bình hành có tổng số đo là 180 độ.

2.3. Tính Chất Về Đường Chéo

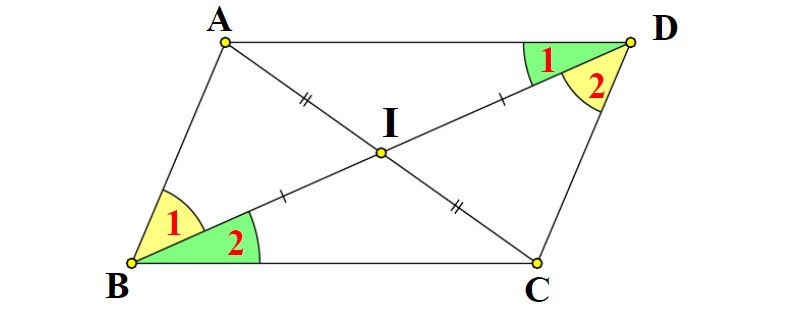
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường: Điểm giao nhau của hai đường chéo chia mỗi đường chéo thành hai đoạn bằng nhau.

3. Dấu Hiệu Nhận Biết Hình Bình Hành: Bí Quyết Nhận Diện

Để xác định một tứ giác có phải là hình bình hành hay không, bạn có thể sử dụng các dấu hiệu sau:

3.1. Dấu Hiệu Dựa Vào Cạnh

• Tứ giác có các cạnh đối song song là hình bình hành.
• Tứ giác có các cạnh đối bằng nhau là hình bình hành.
• Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

3.2. Dấu Hiệu Dựa Vào Góc

• Tứ giác có các góc đối bằng nhau là hình bình hành.

3.3. Dấu Hiệu Dựa Vào Đường Chéo

• Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

4. Các Công Thức Liên Quan Đến Hình Bình Hành: Tính Toán Dễ Dàng

4.1. Chu Vi Hình Bình Hành

Chu vi của hình bình hành là tổng độ dài của bốn cạnh. Vì các cạnh đối diện bằng nhau, công thức tính chu vi hình bình hành là:

C = 2 x (a + b)

Trong đó:

• C là chu vi hình bình hành.
• a và b là độ dài của hai cạnh kề nhau.

4.2. Diện Tích Hình Bình Hành

Diện tích của hình bình hành được tính bằng tích của độ dài cạnh đáy và chiều cao tương ứng. Công thức tính diện tích hình bình hành là:

S = a x h

Trong đó:

• S là diện tích hình bình hành.
• a là độ dài cạnh đáy.
• h là chiều cao, là khoảng cách vuông góc từ cạnh đáy đến cạnh đối diện.

5. Các Dạng Toán Về Hình Bình Hành Thường Gặp (Tiểu Học & THCS)

5.1. Dạng 1: Nhận Biết và Chứng Minh Hình Bình Hành

• Bài tập: Cho một tứ giác, chứng minh tứ giác đó là hình bình hành dựa vào các dấu hiệu nhận biết.
• Phương pháp giải: Sử dụng các dấu hiệu nhận biết hình bình hành để chứng minh. Ví dụ, chứng minh các cạnh đối song song, các cạnh đối bằng nhau, hoặc hai đường chéo cắt nhau tại trung điểm mỗi đường.

Ví dụ: Cho tứ giác ABCD có AB // CD và AB = CD. Chứng minh ABCD là hình bình hành.

Giải:

Vì AB // CD và AB = CD (giả thiết), theo dấu hiệu nhận biết, tứ giác ABCD là hình bình hành.

5.2. Dạng 2: Tính Chu Vi và Diện Tích Hình Bình Hành

• Bài tập: Cho hình bình hành với độ dài các cạnh và chiều cao, yêu cầu tính chu vi và diện tích.
• Phương pháp giải: Áp dụng trực tiếp các công thức tính chu vi và diện tích hình bình hành.

Ví dụ: Cho hình bình hành ABCD có AB = 5cm, BC = 3cm và chiều cao AH (từ A xuống CD) là 2cm. Tính chu vi và diện tích hình bình hành ABCD.

Giải:

• Chu vi hình bình hành ABCD là: C = 2 x (AB + BC) = 2 x (5 + 3) = 16cm.
• Diện tích hình bình hành ABCD là: S = CD x AH = 5 x 2 = 10cm².

5.3. Dạng 3: Sử Dụng Tính Chất Hình Bình Hành Để Giải Toán

• Bài tập: Sử dụng các tính chất về cạnh, góc, đường chéo của hình bình hành để giải các bài toán liên quan.
• Phương pháp giải: Vận dụng linh hoạt các tính chất của hình bình hành để tìm ra mối liên hệ giữa các yếu tố trong bài toán, từ đó giải quyết yêu cầu.

Ví dụ: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Biết AO = 4cm. Tính độ dài AC.

Giải:

Vì O là giao điểm của hai đường chéo trong hình bình hành ABCD, nên O là trung điểm của AC.

Vậy AC = 2 x AO = 2 x 4 = 8cm.

5.4. Dạng 4: Bài Toán Thực Tế Liên Quan Đến Hình Bình Hành

• Bài tập: Các bài toán có nội dung liên quan đến thực tế, yêu cầu học sinh vận dụng kiến thức về hình bình hành để giải quyết.
• Phương pháp giải: Đọc kỹ đề bài, xác định các yếu tố liên quan đến hình bình hành, sau đó áp dụng các công thức và tính chất để giải quyết bài toán.

Ví dụ: Một khu vườn hình bình hành có chiều dài cạnh đáy là 10m và chiều cao tương ứng là 6m. Người ta muốn lát gạch cho khu vườn đó. Biết mỗi viên gạch có diện tích 0.5m². Hỏi cần bao nhiêu viên gạch để lát hết khu vườn?

Giải:

• Diện tích khu vườn hình bình hành là: S = 10 x 6 = 60m².
• Số viên gạch cần để lát hết khu vườn là: 60 / 0.5 = 120 viên.

6. Bài Tập Về Hình Bình Hành Để Bé Luyện Tập: Nâng Cao Kỹ Năng

(Bạn có thể tìm kiếm và thêm các bài tập phù hợp với trình độ của học sinh tiểu học và THCS vào đây)

Ví dụ:

1. Cho hình bình hành ABCD có AB = 8cm, BC = 5cm. Tính chu vi hình bình hành ABCD.
2. Cho hình bình hành MNPQ có MN = 6cm và chiều cao từ P xuống MN là 4cm. Tính diện tích hình bình hành MNPQ.
3. Vẽ một hình bình hành ABCD có AB = 7cm, BC = 4cm và góc ABC = 60 độ.

7. Bí Quyết Giúp Bé Học, Ghi Nhớ Kiến Thức Hình Bình Hành Hiệu Quả: Mẹo Hay Cho Phụ Huynh

7.1. Học Toán Hình Thú Vị Cùng Bé Với Tic.edu.vn

tic.edu.vn cung cấp nguồn tài liệu phong phú, đa dạng về hình bình hành và các chủ đề toán học khác, giúp bé học tập một cách hiệu quả và thú vị. Với tic.edu.vn, việc học toán không còn là gánh nặng mà trở thành một hành trình khám phá đầy hứng khởi.

• Giao diện trực quan, dễ sử dụng: tic.edu.vn được thiết kế với giao diện thân thiện, dễ dàng thao tác, giúp bé nhanh chóng làm quen và sử dụng.
• Nội dung đa dạng, phong phú: tic.edu.vn cung cấp đầy đủ các kiến thức về hình bình hành, từ định nghĩa, tính chất, dấu hiệu nhận biết đến các bài tập vận dụng.
• Phương pháp học tập tương tác: tic.edu.vn sử dụng các hình ảnh minh họa sinh động, các ví dụ thực tế và các bài tập tương tác để giúp bé hiểu bài một cách dễ dàng.
• Cộng đồng học tập sôi nổi: tic.edu.vn có một cộng đồng học tập lớn mạnh, nơi bé có thể giao lưu, học hỏi và chia sẻ kiến thức với các bạn học khác.

7.2. Giúp Bé Nắm Vững Lý Thuyết Hình Bình Hành

Để giải được bài tập, bé cần nắm vững lý thuyết về hình bình hành. Hãy giúp bé hiểu rõ các khái niệm, tính chất, dấu hiệu nhận biết và công thức liên quan. Sử dụng hình ảnh minh họa, ví dụ thực tế để giúp bé hình dung và ghi nhớ kiến thức một cách dễ dàng.

7.3. Cùng Bé Thực Hành Thường Xuyên Rất Cần Thiết

Thực hành là chìa khóa để bé nắm vững kiến thức và phát triển kỹ năng giải toán. Hãy tạo cơ hội để bé thực hành giải các bài tập về hình bình hành, từ cơ bản đến nâng cao. Khuyến khích bé tự tìm tòi, khám phá các cách giải khác nhau.

7.4. Sử Dụng Đồ Dùng Trực Quan Để Minh Họa

Sử dụng các đồ dùng trực quan như que tính, giấy, kéo để tạo ra các hình bình hành và minh họa các tính chất của chúng. Điều này giúp bé hiểu rõ hơn về hình bình hành và ghi nhớ kiến thức một cách trực quan.

7.5. Liên Hệ Với Thực Tế

Tìm kiếm các ví dụ về hình bình hành trong cuộc sống hàng ngày, chẳng hạn như khung cửa sổ, mặt bàn, viên gạch lát nền. Điều này giúp bé thấy được tính ứng dụng của hình bình hành và tăng thêm hứng thú học tập.

7.6. Tạo Không Gian Học Tập Thoải Mái

Đảm bảo bé có một không gian học tập yên tĩnh, thoải mái và đầy đủ ánh sáng. Loại bỏ các yếu tố gây xao nhãng như TV, điện thoại. Khuyến khích bé đặt câu hỏi và thảo luận về các vấn đề chưa hiểu.

8. FAQ – Các Câu Hỏi Thường Gặp Về Hình Bình Hành

1. Hình bình hành có phải là hình vuông không? Không, hình vuông là một trường hợp đặc biệt của hình bình hành, có thêm điều kiện là tất cả các cạnh bằng nhau và các góc đều là góc vuông.
2. Làm thế nào để tính diện tích hình bình hành khi chỉ biết độ dài hai cạnh kề nhau? Bạn cần biết thêm chiều cao tương ứng với một trong hai cạnh đó.
3. Hình bình hành có tâm đối xứng không? Có, hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
4. Hình bình hành có trục đối xứng không? Không, hình bình hành không có trục đối xứng (trừ hình thoi và hình chữ nhật là các trường hợp đặc biệt).
5. Có những loại bài tập nào về hình bình hành? Các loại bài tập thường gặp bao gồm: nhận biết và chứng minh hình bình hành, tính chu vi và diện tích, sử dụng tính chất để giải toán, và các bài toán thực tế.
6. Tôi có thể tìm thêm tài liệu học tập về hình bình hành ở đâu? Bạn có thể tìm thấy nhiều tài liệu hữu ích trên tic.edu.vn, bao gồm bài giảng, bài tập, và các ví dụ minh họa.
7. Làm thế nào để giúp con tôi học tốt hình bình hành? Hãy giúp con bạn nắm vững lý thuyết, thực hành thường xuyên, sử dụng đồ dùng trực quan, liên hệ với thực tế và tạo không gian học tập thoải mái.
8. Tôi nên bắt đầu dạy con về hình bình hành từ khi nào? Bạn có thể bắt đầu giới thiệu cho con về hình bình hành từ lớp 4, khi các em bắt đầu làm quen với hình học phẳng.
9. Có những ứng dụng thực tế nào của hình bình hành trong cuộc sống? Hình bình hành xuất hiện trong kiến trúc, nội thất, thiết kế đồ họa, và toán học/vật lý.
10. Làm thế nào để phân biệt hình bình hành với hình thang? Hình bình hành có hai cặp cạnh đối diện song song, trong khi hình thang chỉ có một cặp cạnh đối diện song song.

9. Kết Luận: Hình Bình Hành – Nền Tảng Vững Chắc Cho Toán Học

Hình bình hành là một hình học cơ bản nhưng vô cùng quan trọng, là nền tảng để học sinh tiếp cận với các khái niệm hình học phức tạp hơn. Hiểu rõ về hình bình hành giúp học sinh phát triển tư duy logic, khả năng giải quyết vấn đề và ứng dụng kiến thức vào thực tế.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn và con bạn chinh phục thế giới toán học đầy thú vị! Liên hệ với tic.edu.vn qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.