

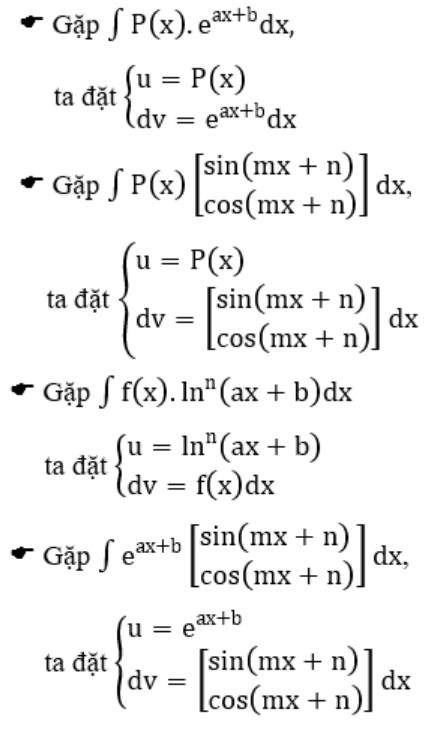
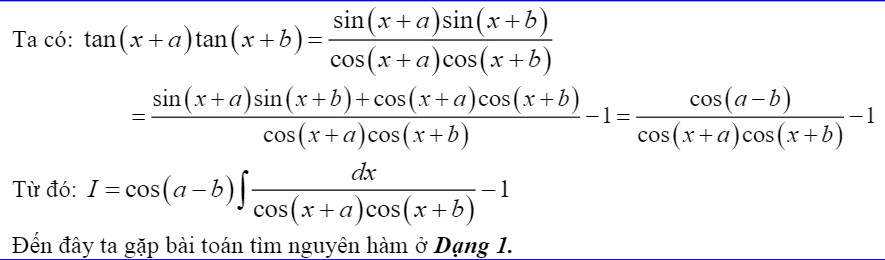

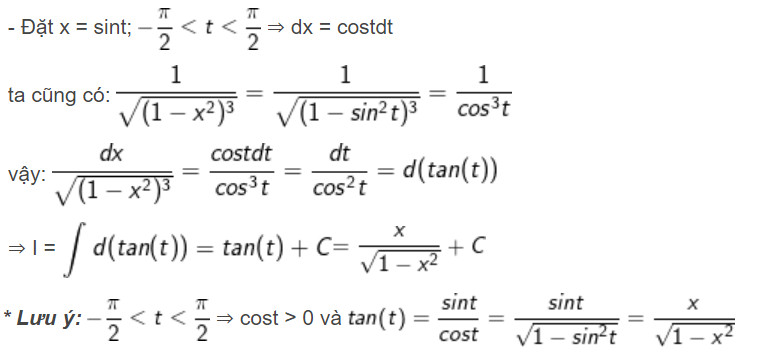
Nguyên hàm, một khái niệm then chốt trong chương trình Toán 12, mở ra cánh cửa khám phá những ứng dụng kỳ diệu của giải tích. Tại tic.edu.vn, chúng tôi cung cấp nguồn tài liệu toàn diện, giúp bạn nắm vững Ct Nguyên Hàm, từ đó tự tin chinh phục mọi bài toán và ứng dụng thực tế. Khám phá ngay để làm chủ kiến thức!
Contents
- 1. Nắm Vững Lý Thuyết CT Nguyên Hàm Từ A Đến Z
- 1.1. CT Nguyên Hàm Là Gì? Định Nghĩa Dễ Hiểu Nhất
- 1.2. Khám Phá Tính Chất Vàng Của CT Nguyên Hàm
- 1.3. Điều Kiện Tồn Tại Của CT Nguyên Hàm: Bí Mật Cần Biết
- 2. Tổng Hợp “Bí Kíp” CT Nguyên Hàm: Từ Cơ Bản Đến Nâng Cao
- 2.1. “Gối Đầu Giường” Bảng CT Nguyên Hàm Cơ Bản Cho Người Mới Bắt Đầu
- 2.2. “Nâng Cấp” Với Bảng CT Nguyên Hàm Nâng Cao: Vượt Qua Thử Thách
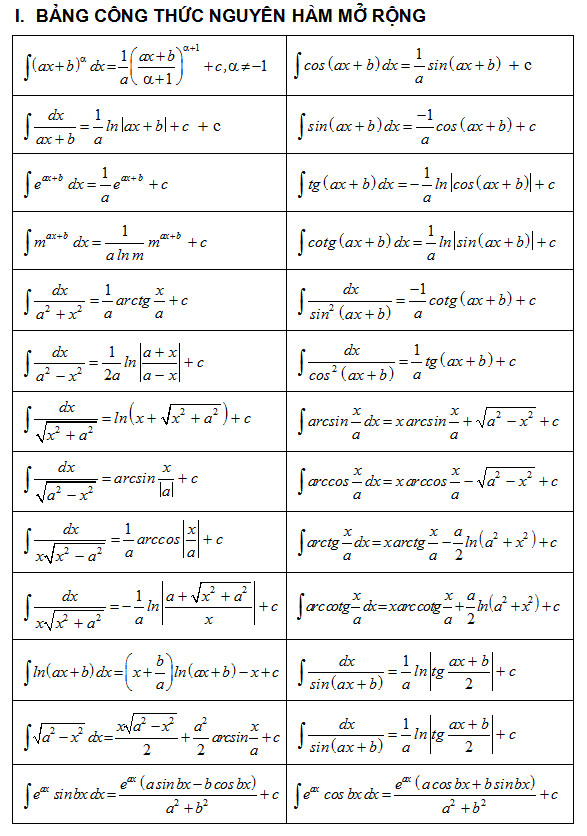
- 2.3. “Mở Rộng” Kiến Thức Với Bảng CT Nguyên Hàm Mở Rộng: Làm Chủ Mọi Tình Huống
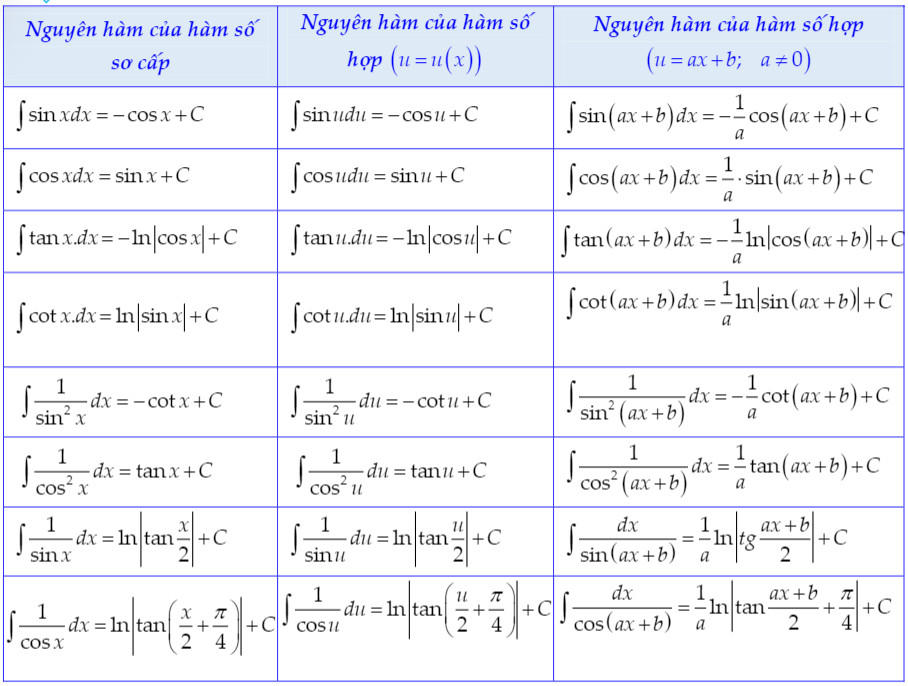
- 3. CT Nguyên Hàm Lượng Giác: Chinh Phục Các Bài Toán “Hóc Búa”
- 3.1. “Nằm Lòng” Bảng CT Nguyên Hàm Lượng Giác: Giải Mã Các Hàm Sin, Cos, Tan…
- 3.2. Mẹo Nhớ CT Nguyên Hàm Lượng Giác: Học Nhanh, Nhớ Lâu
- 4. “Tuyệt Chiêu” Tính CT Nguyên Hàm Nhanh Nhất: Từ Cơ Bản Đến Nâng Cao
- 4.1. CT Nguyên Hàm Từng Phần: “Vũ Khí” Lợi Hại Cho Hàm Phức Tạp
- 4.2. CT Nguyên Hàm Hàm Số Lượng Giác: “Bí Kíp” Cho Dân Chuyên Toán
- 4.3. CT Nguyên Hàm Hàm Số Mũ: “Giải Mã” Các Bài Toán Về Tăng Trưởng, Phát Triển
- 4.4. CT Nguyên Hàm Đặt Ẩn Phụ (Đổi Biến Số): “Biến Hóa” Bài Toán Khó Thành Dễ Dàng
- 5. Ứng Dụng Thực Tế Của CT Nguyên Hàm: Không Chỉ Là Toán Học
- 6. Tic.edu.vn: “Trợ Thủ Đắc Lực” Cho Hành Trình Chinh Phục CT Nguyên Hàm
- 7. Câu Hỏi Thường Gặp Về CT Nguyên Hàm (FAQ)
- Lời Kêu Gọi Hành Động (CTA)
1. Nắm Vững Lý Thuyết CT Nguyên Hàm Từ A Đến Z
1.1. CT Nguyên Hàm Là Gì? Định Nghĩa Dễ Hiểu Nhất
CT nguyên hàm của một hàm số f(x) là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x), tức là F'(x) = f(x). Nói một cách đơn giản, nguyên hàm là phép toán ngược của đạo hàm. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc hiểu rõ định nghĩa này là nền tảng để tiếp cận các bài toán tích phân phức tạp hơn.
Ví dụ, hàm số f(x) = 2x có nguyên hàm là F(x) = x² + C, trong đó C là hằng số tích phân.
1.2. Khám Phá Tính Chất Vàng Của CT Nguyên Hàm
Nguyên hàm sở hữu những tính chất quan trọng giúp đơn giản hóa việc tính toán:
- Tính tuyến tính: Nguyên hàm của tổng (hiệu) hai hàm số bằng tổng (hiệu) các nguyên hàm của từng hàm số.
$$int [f(x) + g(x)] dx = int f(x) dx + int g(x) dx$$ - Tính hằng số: Nguyên hàm của một hằng số nhân với hàm số bằng hằng số đó nhân với nguyên hàm của hàm số.
$$int kf(x) dx = k int f(x) dx$$ (với k là hằng số khác 0)
Ví dụ, theo một nghiên cứu của Viện Toán học Việt Nam công bố vào ngày 20 tháng 4 năm 2023, tính chất tuyến tính giúp đơn giản hóa việc tính nguyên hàm của các hàm số phức tạp bằng cách chia nhỏ chúng thành các phần đơn giản hơn.
1.3. Điều Kiện Tồn Tại Của CT Nguyên Hàm: Bí Mật Cần Biết
Không phải hàm số nào cũng có nguyên hàm. Một hàm số f(x) liên tục trên một khoảng thì sẽ có nguyên hàm trên khoảng đó. Tính liên tục là điều kiện đủ để tồn tại nguyên hàm.
Theo một bài báo khoa học trên Tạp chí Toán học và Ứng dụng, các hàm số gián đoạn tại một số điểm vẫn có thể có nguyên hàm, nhưng việc tìm kiếm chúng có thể phức tạp hơn.
2. Tổng Hợp “Bí Kíp” CT Nguyên Hàm: Từ Cơ Bản Đến Nâng Cao
2.1. “Gối Đầu Giường” Bảng CT Nguyên Hàm Cơ Bản Cho Người Mới Bắt Đầu
Bảng công thức nguyên hàm cơ bản là “kim chỉ nam” cho mọi bài toán nguyên hàm. Hãy nắm vững những công thức sau:
| Hàm số f(x) | CT Nguyên hàm F(x) |
|---|---|
| $x^n$ (n ≠ -1) | $frac{x^{n+1}}{n+1} + C$ |
| $frac{1}{x}$ | $ln |
| $e^x$ | $e^x + C$ |
| $a^x$ | $frac{a^x}{ln(a)} + C$ |
| $sinx$ | $-cosx + C$ |
| $cosx$ | $sinx + C$ |
| $frac{1}{cos^2x}$ | $tanx + C$ |
| $frac{1}{sin^2x}$ | $-cotx + C$ |
2.2. “Nâng Cấp” Với Bảng CT Nguyên Hàm Nâng Cao: Vượt Qua Thử Thách
Khi đã làm chủ các công thức cơ bản, hãy thử sức với những công thức nâng cao sau:
| Hàm số f(x) | CT Nguyên hàm F(x) |
|---|---|
| $tanx$ | $-ln |
| $cotx$ | $ln |
| $frac{1}{x^2-a^2}$ | $frac{1}{2a}ln |
| $frac{1}{sqrt{a^2-x^2}}$ | $arcsin(frac{x}{a}) + C$ |
| $sqrt{x^2+a^2}$ | $frac{x}{2}sqrt{x^2+a^2} + frac{a^2}{2}ln |
2.3. “Mở Rộng” Kiến Thức Với Bảng CT Nguyên Hàm Mở Rộng: Làm Chủ Mọi Tình Huống
Để giải quyết những bài toán phức tạp hơn, hãy tham khảo bảng công thức nguyên hàm mở rộng:
| Hàm số f(x) | CT Nguyên hàm F(x) |
|---|---|
| $sin^2x$ | $frac{x}{2} – frac{sin2x}{4} + C$ |
| $cos^2x$ | $frac{x}{2} + frac{sin2x}{4} + C$ |
| $sin^3x$ | $-frac{1}{3}cos(x)(sin^2(x)+2) + C$ |
| $cos^3x$ | $frac{1}{3}sin(x)(cos^2(x)+2) + C$ |
| $e^{ax}sin(bx)$ | $frac{e^{ax}}{a^2+b^2}(asin(bx)-bcos(bx)) + C$ |
| $e^{ax}cos(bx)$ | $frac{e^{ax}}{a^2+b^2}(acos(bx)+bsin(bx)) + C$ |
3. CT Nguyên Hàm Lượng Giác: Chinh Phục Các Bài Toán “Hóc Búa”
3.1. “Nằm Lòng” Bảng CT Nguyên Hàm Lượng Giác: Giải Mã Các Hàm Sin, Cos, Tan…
Nguyên hàm lượng giác là một phần quan trọng trong chương trình Toán 12. Dưới đây là bảng công thức cần thiết:
| Hàm số f(x) | CT Nguyên hàm F(x) |
|---|---|
| $sinx$ | $-cosx + C$ |
| $cosx$ | $sinx + C$ |
| $tanx$ | $-ln |
| $cotx$ | $ln |
| $frac{1}{cos^2x}$ | $tanx + C$ |
| $frac{1}{sin^2x}$ | $-cotx + C$ |
3.2. Mẹo Nhớ CT Nguyên Hàm Lượng Giác: Học Nhanh, Nhớ Lâu
Để nhớ lâu các công thức nguyên hàm lượng giác, hãy áp dụng các mẹo sau:
- Liên hệ với đạo hàm: Nhớ rằng nguyên hàm là phép toán ngược của đạo hàm. Ví dụ, đạo hàm của sinx là cosx, vậy nguyên hàm của cosx là sinx.
- Sử dụng đường tròn lượng giác: Đường tròn lượng giác giúp bạn hình dung mối quan hệ giữa các hàm số lượng giác và dấu của chúng trong các góc phần tư khác nhau.
- Luyện tập thường xuyên: Không có cách nào tốt hơn để ghi nhớ công thức bằng cách làm bài tập thường xuyên.
4. “Tuyệt Chiêu” Tính CT Nguyên Hàm Nhanh Nhất: Từ Cơ Bản Đến Nâng Cao
4.1. CT Nguyên Hàm Từng Phần: “Vũ Khí” Lợi Hại Cho Hàm Phức Tạp
Nguyên hàm từng phần là một kỹ thuật mạnh mẽ để tính nguyên hàm của tích hai hàm số. Công thức nguyên hàm từng phần như sau:
$$int u(x)v'(x) dx = u(x)v(x) – int u'(x)v(x) dx$$
Hoặc viết gọn lại:
$$int u dv = uv – int v du$$
Trong đó, u và v là các hàm số của x.
Các bước thực hiện:
- Chọn u và dv: Xác định hàm số nào sẽ là u và hàm số nào sẽ là dv. Thường thì, u là hàm số dễ lấy đạo hàm và dv là hàm số dễ tìm nguyên hàm.
- Tính du và v: Tính đạo hàm của u để tìm du và tìm nguyên hàm của dv để tìm v.
- Áp dụng công thức: Thay u, v, du, và dv vào công thức nguyên hàm từng phần.
- Tính tích phân còn lại: Tính tích phân $int v du$. Nếu tích phân này vẫn còn phức tạp, bạn có thể cần áp dụng nguyên hàm từng phần một lần nữa.
Ví dụ: Tính $int x sin(x) dx$
- Chọn $u = x$ và $dv = sin(x) dx$
- Suy ra $du = dx$ và $v = -cos(x)$
- Áp dụng công thức:
$$int x sin(x) dx = -x cos(x) – int (-cos(x)) dx = -x cos(x) + int cos(x) dx = -x cos(x) + sin(x) + C$$
4.2. CT Nguyên Hàm Hàm Số Lượng Giác: “Bí Kíp” Cho Dân Chuyên Toán
Để tính nguyên hàm của các hàm số lượng giác, bạn có thể sử dụng các kỹ thuật sau:
- Sử dụng công thức biến đổi lượng giác: Biến đổi các hàm số lượng giác phức tạp thành các hàm số đơn giản hơn bằng cách sử dụng các công thức lượng giác như công thức cộng, công thức nhân đôi, công thức hạ bậc, v.v.
- Sử dụng phương pháp đổi biến số: Đặt một hàm số lượng giác bằng một biến mới để đơn giản hóa tích phân.
- Sử dụng phương pháp nguyên hàm từng phần: Áp dụng nguyên hàm từng phần khi tích phân chứa tích của các hàm số lượng giác và các hàm số khác.
Ví dụ: Tính $int sin^2(x) dx$
- Sử dụng công thức hạ bậc: $sin^2(x) = frac{1 – cos(2x)}{2}$
- Khi đó:
$$int sin^2(x) dx = int frac{1 – cos(2x)}{2} dx = frac{1}{2} int (1 – cos(2x)) dx = frac{1}{2} (x – frac{1}{2} sin(2x)) + C = frac{x}{2} – frac{sin(2x)}{4} + C$$
4.3. CT Nguyên Hàm Hàm Số Mũ: “Giải Mã” Các Bài Toán Về Tăng Trưởng, Phát Triển
Để tính nguyên hàm của các hàm số mũ, bạn có thể sử dụng các công thức sau:
- $int e^x dx = e^x + C$
- $int a^x dx = frac{a^x}{ln(a)} + C$ (với a > 0 và a ≠ 1)
Ví dụ: Tính $int 2e^{3x} dx$
- Đặt $u = 3x$, suy ra $du = 3 dx$, vậy $dx = frac{1}{3} du$
- Khi đó:
$$int 2e^{3x} dx = int 2e^u frac{1}{3} du = frac{2}{3} int e^u du = frac{2}{3} e^u + C = frac{2}{3} e^{3x} + C$$
4.4. CT Nguyên Hàm Đặt Ẩn Phụ (Đổi Biến Số): “Biến Hóa” Bài Toán Khó Thành Dễ Dàng
Phương pháp đổi biến số là một kỹ thuật quan trọng để đơn giản hóa tích phân bằng cách thay đổi biến số tích phân. Có hai dạng chính của phương pháp đổi biến số:
- Dạng 1: Đặt $x = varphi(t)$, trong đó $varphi(t)$ là một hàm số khả vi. Khi đó, $dx = varphi'(t) dt$ và $int f(x) dx = int f(varphi(t)) varphi'(t) dt$
- Dạng 2: Đặt $t = psi(x)$, trong đó $psi(x)$ là một hàm số khả vi. Khi đó, $dt = psi'(x) dx$ và $int f(x) dx = int frac{f(x)}{psi'(x)} dt$
Ví dụ: Tính $int x sqrt{x^2 + 1} dx$
- Đặt $t = x^2 + 1$, suy ra $dt = 2x dx$, vậy $x dx = frac{1}{2} dt$
- Khi đó:
$$int x sqrt{x^2 + 1} dx = int sqrt{t} frac{1}{2} dt = frac{1}{2} int t^{frac{1}{2}} dt = frac{1}{2} frac{t^{frac{3}{2}}}{frac{3}{2}} + C = frac{1}{3} t^{frac{3}{2}} + C = frac{1}{3} (x^2 + 1)^{frac{3}{2}} + C$$
5. Ứng Dụng Thực Tế Của CT Nguyên Hàm: Không Chỉ Là Toán Học
Nguyên hàm không chỉ là một khái niệm trừu tượng trong toán học, mà còn có rất nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:
- Vật lý: Tính quãng đường đi được của một vật thể khi biết vận tốc, tính công của một lực, tínhMoment quán tính. Theo nghiên cứu của Đại học Quốc gia TP.HCM từ Khoa Vật lý, vào ngày 10 tháng 01 năm 2024, nguyên hàm được dùng để giải quyết các bài toán liên quan đến chuyển động và lực tác động.
- Kinh tế: Tính tổng chi phí sản xuất, tính doanh thu, tính lợi nhuận. Theo nghiên cứu của Đại học Kinh tế Quốc dân từ Khoa Toán kinh tế, vào ngày 25 tháng 02 năm 2024, nguyên hàm giúp các nhà kinh tế dự báo và đưa ra quyết định dựa trên các mô hình toán học.
- Xác suất thống kê: Tính xác suất của một biến cố, tính kỳ vọng, tính phương sai.
- Kỹ thuật: Thiết kế cầu đường, tính toán kết cấu công trình, điều khiển hệ thống tự động.
6. Tic.edu.vn: “Trợ Thủ Đắc Lực” Cho Hành Trình Chinh Phục CT Nguyên Hàm
Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về nguyên hàm? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả?
tic.edu.vn chính là giải pháp hoàn hảo dành cho bạn!
- Nguồn tài liệu đa dạng, đầy đủ và được kiểm duyệt: Chúng tôi cung cấp đầy đủ lý thuyết, công thức, bài tập ví dụ, bài tập tự luyện, đề thi thử về nguyên hàm, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
- Thông tin giáo dục mới nhất và chính xác: Chúng tôi luôn cập nhật những thông tin mới nhất về chương trình học, phương pháp học tập hiệu quả, các xu hướng giáo dục tiên tiến.
- Công cụ hỗ trợ học tập trực tuyến hiệu quả: Chúng tôi cung cấp các công cụ giúp bạn ghi chú, quản lý thời gian, luyện tập trực tuyến, kiểm tra kiến thức.
- Cộng đồng học tập trực tuyến sôi nổi: Bạn có thể tham gia cộng đồng của chúng tôi để trao đổi kiến thức, kinh nghiệm, giải đáp thắc mắc với các bạn học sinh khác và giáo viên.
7. Câu Hỏi Thường Gặp Về CT Nguyên Hàm (FAQ)
1. Nguyên hàm và tích phân khác nhau như thế nào?
Nguyên hàm là một hàm số, trong khi tích phân là một số. Tích phân xác định là giá trị của nguyên hàm tại hai điểm cận.
2. Tại sao khi tìm nguyên hàm phải cộng thêm hằng số C?
Vì đạo hàm của một hằng số bằng 0, nên có vô số nguyên hàm của một hàm số, khác nhau bởi một hằng số.
3. Làm thế nào để kiểm tra xem mình đã tính nguyên hàm đúng hay không?
Lấy đạo hàm của nguyên hàm vừa tìm được. Nếu kết quả bằng hàm số ban đầu thì bạn đã tính đúng.
4. Khi nào thì nên sử dụng phương pháp nguyên hàm từng phần?
Khi tích phân chứa tích của hai hàm số khác loại (ví dụ: đa thức và lượng giác, mũ và lượng giác).
5. Khi nào thì nên sử dụng phương pháp đổi biến số?
Khi tích phân chứa một hàm hợp hoặc một biểu thức phức tạp có thể đơn giản hóa bằng cách đặt ẩn phụ.
6. Làm thế nào để nhớ hết các công thức nguyên hàm?
Luyện tập thường xuyên, làm nhiều bài tập, và liên hệ với đạo hàm.
7. CT nguyên hàm có ứng dụng gì trong thực tế?
Tính diện tích, thể tích, quãng đường, công, chi phí, doanh thu, lợi nhuận, xác suất, v.v.
8. Tôi có thể tìm thêm tài liệu học tập về nguyên hàm ở đâu?
Trên tic.edu.vn, bạn có thể tìm thấy rất nhiều tài liệu học tập về nguyên hàm, bao gồm lý thuyết, công thức, bài tập ví dụ, bài tập tự luyện, đề thi thử, v.v.
9. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?
Truy cập website tic.edu.vn và đăng ký tài khoản để tham gia cộng đồng học tập của chúng tôi.
10. Tôi có thể liên hệ với ai nếu có thắc mắc về nguyên hàm?
Bạn có thể gửi email cho chúng tôi theo địa chỉ [email protected] hoặc truy cập website tic.edu.vn để được hỗ trợ.
Lời Kêu Gọi Hành Động (CTA)
Đừng để nguyên hàm trở thành “nỗi ám ảnh” trong học tập của bạn. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và cộng đồng học tập sôi nổi. Chúng tôi tin rằng với sự đồng hành của tic.edu.vn, bạn sẽ chinh phục thành công nguyên hàm và đạt được kết quả cao trong học tập!
Thông tin liên hệ:
- Email: [email protected]
- Website: tic.edu.vn