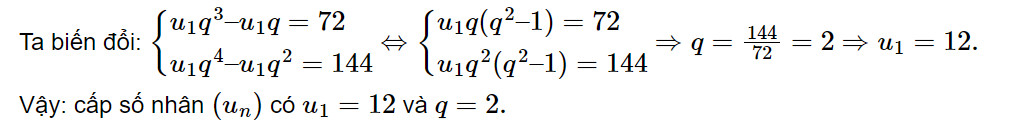
**CT Cấp Số Nhân: Định Nghĩa, Ứng Dụng và Bài Tập Chi Tiết**

Ct Cấp Số Nhân là một chủ đề quan trọng trong chương trình toán học phổ thông, đặc biệt đối với học sinh THPT và những ai quan tâm đến lĩnh vực tài chính, kinh tế. Tại tic.edu.vn, chúng tôi cung cấp tài liệu đầy đủ, chi tiết về CT cấp số nhân, giúp bạn nắm vững kiến thức và ứng dụng hiệu quả. CT cấp số nhân không chỉ là một khái niệm toán học, mà còn là công cụ hữu ích trong nhiều lĩnh vực thực tế như tính lãi kép, dự báo tăng trưởng, và phân tích chuỗi số.

1. CT Cấp Số Nhân Là Gì? Định Nghĩa và Ví Dụ Minh Họa

CT cấp số nhân (CSN) là một dãy số, hữu hạn hoặc vô hạn, trong đó mỗi số hạng, kể từ số hạng thứ hai, đều bằng tích của số hạng đứng ngay trước nó với một số không đổi, gọi là công bội. Hiểu một cách đơn giản, mỗi số hạng trong CSN được tạo ra bằng cách nhân số hạng trước đó với một giá trị cố định.

Định nghĩa: Dãy số (u_n) là một CT cấp số nhân nếu và chỉ nếu tồn tại một số q (công bội) sao cho u_n = u_n-1 q với mọi n ≥ 2 và n thuộc tập số tự nhiên khác 0 (N).

Ví dụ:

• Dãy số 2, 4, 8, 16, 32,… là một CT cấp số nhân với số hạng đầu u₁ = 2 và công bội q = 2.
• Dãy số 5, 15, 45, 135, 405,… là một CT cấp số nhân với số hạng đầu u₁ = 5 và công bội q = 3.
• Dãy số 1, -2, 4, -8, 16,… là một CT cấp số nhân với số hạng đầu u₁ = 1 và công bội q = -2.

Lưu ý:

• Công bội q có thể là số dương, số âm hoặc bằng 0.
• Nếu q = 1, CT cấp số nhân trở thành một dãy số không đổi (tất cả các số hạng đều bằng nhau).
• Nếu q = 0 và số hạng đầu u₁ khác 0, tất cả các số hạng sau số hạng đầu đều bằng 0.

1.1. Phân biệt CT Cấp Số Nhân và Cấp Số Cộng

Để phân biệt CT cấp số nhân và cấp số cộng (CSC), cần nhớ rõ định nghĩa của từng loại. CSC là dãy số mà mỗi số hạng (kể từ số hạng thứ hai) bằng tổng của số hạng đứng trước nó với một số không đổi (công sai). Trong khi đó, CT cấp số nhân là dãy số mà mỗi số hạng (kể từ số hạng thứ hai) bằng tích của số hạng đứng trước nó với một số không đổi (công bội).

Ví dụ:

• Dãy số 1, 3, 5, 7, 9,… là một cấp số cộng với công sai d = 2.
• Dãy số 2, 6, 18, 54, 162,… là một CT cấp số nhân với công bội q = 3.

2. Công Bội q Của CT Cấp Số Nhân: Cách Xác Định và Ứng Dụng

Công bội q là một yếu tố then chốt để xác định và làm việc với CT cấp số nhân. Nó quyết định sự tăng trưởng hoặc suy giảm của dãy số.

Công thức tính công bội:

q = u_n+1 / u_n (với mọi n ≥ 1)

Ví dụ:

• Cho CT cấp số nhân có u₁ = 3 và u₂ = 9. Tính công bội q.

  q = u₂ / u₁ = 9 / 3 = 3

• Cho CT cấp số nhân có u₃ = 8 và u₄ = 16. Tính công bội q.

  q = u₄ / u₃ = 16 / 8 = 2

Ứng dụng của công bội:

• Xác định tính chất của CT cấp số nhân (tăng, giảm, không đổi).
• Tìm các số hạng còn thiếu trong CT cấp số nhân.
• Tính tổng của CT cấp số nhân.
• Giải các bài toán liên quan đến lãi kép, tăng trưởng dân số, v.v.

2.1. Các Trường Hợp Đặc Biệt Của Công Bội

• q > 1: CT cấp số nhân tăng (các số hạng ngày càng lớn hơn).
• 0 < q < 1: CT cấp số nhân giảm (các số hạng ngày càng nhỏ hơn).
• q < 0: CT cấp số nhân có các số hạng xen kẽ dấu (âm và dương).
• q = 1: CT cấp số nhân là dãy số không đổi.
• q = 0: CT cấp số nhân có tất cả các số hạng sau số hạng đầu tiên đều bằng 0.

3. Tính Chất Quan Trọng Của CT Cấp Số Nhân: Nắm Vững Để Giải Bài Tập

CT cấp số nhân có một số tính chất quan trọng, giúp giải quyết các bài toán liên quan một cách hiệu quả.

3.1. Tính chất 1: Bình phương của một số hạng

Trong một CT cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và số hạng cuối, nếu CT cấp số nhân là hữu hạn) bằng tích của hai số hạng đứng kề nó.

u_k² = u_k-1 * u_k+1 (với mọi k ≥ 2)

3.2. Tính chất 2: Số hạng tổng quát

Nếu CT cấp số nhân có số hạng đầu u₁ và công bội q, thì số hạng tổng quát u_n được tính bằng công thức:

u_n = u₁ * q^n-1

Ví dụ: Cho CT cấp số nhân (u_n) với u₁ = 2 và q = 3. Tìm u₅.

u₅ = u₁ q^5-1 = 2 3⁴ = 2 * 81 = 162

3.3. Tính chất 3: Tổng n số hạng đầu

Tổng n số hạng đầu tiên của CT cấp số nhân (S_n) được tính bằng công thức:

S_n = u₁ * (1 – qⁿ) / (1 – q) (khi q ≠ 1)

S_n = n * u₁ (khi q = 1)

Ví dụ: Tính tổng 5 số hạng đầu tiên của CT cấp số nhân 2, 4, 8, 16, 32.

u₁ = 2, q = 2, n = 5

S₅ = 2 (1 – 2⁵) / (1 – 2) = 2 (1 – 32) / (-1) = 2 * (-31) / (-1) = 62

3.4. Lưu Ý Quan Trọng Khi Sử Dụng Các Tính Chất

• Luôn kiểm tra điều kiện của công bội q (q ≠ 1) trước khi áp dụng công thức tính tổng.
• Khi q = 1, CT cấp số nhân trở thành dãy số không đổi, công thức tính tổng sẽ khác.
• Nắm vững các tính chất giúp giải nhanh các bài toán trắc nghiệm và tự luận.

4. Tổng Hợp Các Công Thức Tính CT Cấp Số Nhân Cơ Bản: Giải Nhanh Bài Tập

Để giải quyết các bài toán về CT cấp số nhân một cách nhanh chóng và chính xác, việc nắm vững các công thức là vô cùng quan trọng. Dưới đây là tổng hợp các công thức cơ bản và thường dùng nhất.

4.1. Dạng 1: Nhận Biết CT Cấp Số Nhân

Phương pháp:

1. Tính tỉ số q = u_n+1 / u_n với mọi n ≥ 1.

2. Kết luận:

   • Nếu q là một hằng số (không đổi), thì dãy (u_n) là CT cấp số nhân.
   • Nếu q thay đổi theo n, thì dãy (u_n) không phải là CT cấp số nhân.

Ví dụ:

• Dãy số 2, 6, 18, 54,… có phải là CT cấp số nhân không?

  q = 6/2 = 18/6 = 54/18 = 3 (hằng số)

  Vậy dãy số này là CT cấp số nhân với công bội q = 3.

• Dãy số 1, 4, 9, 16,… có phải là CT cấp số nhân không?

  q₁ = 4/1 = 4, q₂ = 9/4 = 2.25

  Vì q₁ ≠ q₂, nên dãy số này không phải là CT cấp số nhân.

4.2. Dạng 2: Tìm Công Bội q

Phương pháp: Sử dụng công thức q = u_n+1 / u_n hoặc các tính chất của CT cấp số nhân để biến đổi và tìm q.

Ví dụ:

• Cho CT cấp số nhân (u_n) có u₁ = 2 và u₂ = 4. Tìm q.

  q = u₂ / u₁ = 4 / 2 = 2

• Cho CT cấp số nhân (u_n) có u₁ = 3 và u₂ = -6. Tìm q.

  q = u₂ / u₁ = -6 / 3 = -2

4.3. Dạng 3: Tìm Số Hạng Của CT Cấp Số Nhân

Phương pháp: Sử dụng công thức số hạng tổng quát: u_n = u₁ * q^n-1

Ví dụ:

• Tìm u₁ và q của CT cấp số nhân, biết:

  u₄ – u₂ = 72

  u₅ – u₃ = 144

  Giải:

  u₁q³ – u₁q = 72

  u₁q⁴ – u₁q² = 144

  => u₁q(q² – 1) = 72

  u₁q²(q² – 1) = 144

  => q = 144/72 = 2 => u₁ = 12

  Vậy CT cấp số nhân có u₁ = 12 và q = 2.

4.4. Dạng 4: Tính Tổng n Số Hạng Đầu Tiên

Phương pháp: Sử dụng công thức:

• S_n = u₁ * (1 – qⁿ) / (1 – q) (nếu q ≠ 1)
• S_n = n * u₁ (nếu q = 1)

Ví dụ: Tính tổng S = 2 + 6 + 18 + … + 13122

(u_n) có u₁ = 2 và q = 3.

13122 = u_n = u₁q^n-1 = 2 * 3^n-1 => n = 9

S = S₉ = u₁ (q⁹ – 1) / (q – 1) = 2 (3⁹ – 1) / (3 – 1) = 19682

4.5. Dạng 5: Tìm CT Cấp Số Nhân

Phương pháp: Xác định các yếu tố cơ bản của CT cấp số nhân như số hạng đầu u₁ và công bội q, sau đó suy ra công thức tổng quát.

Ví dụ: Tìm CT cấp số nhân (u_n), biết:

u₁(1 + q⁴) = 82/11

u₁(1 + q + q² + q³ + q⁴) = 11

Giải:

u₁q(1 + q + q²) = 32/11

u₁(1 + q⁴) = 82/11

=> (1 + q⁴) / (q(1 + q + q²)) = 82/39

=> q = 3 hoặc q = 1/3

Khi đó, u₁ = 81/11 hoặc u₁ = 1/11

5. CT Cấp Số Nhân Lùi Vô Hạn: Khái Niệm và Ứng Dụng

CT cấp số nhân lùi vô hạn là một trường hợp đặc biệt của CT cấp số nhân, trong đó công bội q thỏa mãn điều kiện -1 < q < 1.

5.1. Định Nghĩa CT Cấp Số Nhân Lùi Vô Hạn

CT cấp số nhân (u_n) được gọi là lùi vô hạn nếu công bội q của nó thỏa mãn điều kiện -1 < q < 1. Điều này có nghĩa là các số hạng của CT cấp số nhân sẽ ngày càng nhỏ hơn về giá trị tuyệt đối và tiến dần đến 0.

Ví dụ:

• 1/2, 1/4, 1/8, 1/16,… (q = 1/2)
• 1, -1/3, 1/9, -1/27,… (q = -1/3)

5.2. Tổng Của CT Cấp Số Nhân Lùi Vô Hạn

Một trong những ứng dụng quan trọng nhất của CT cấp số nhân lùi vô hạn là tính tổng của nó. Tổng S của CT cấp số nhân lùi vô hạn được tính theo công thức:

S = u₁ / (1 – q)

Ví dụ: Tính tổng S = 1 – 1/3 + 1/9 – 1/27 + …

Đây là tổng của CT cấp số nhân lùi vô hạn với u₁ = 1 và q = -1/3.

S = 1 / (1 – (-1/3)) = 1 / (4/3) = 3/4

5.3. Ứng Dụng Của CT Cấp Số Nhân Lùi Vô Hạn

CT cấp số nhân lùi vô hạn có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:

• Biểu diễn số thập phân vô hạn tuần hoàn: Ví dụ, số 0.777… có thể được biểu diễn dưới dạng tổng của CT cấp số nhân lùi vô hạn.
• Tính diện tích và thể tích: Trong hình học, CT cấp số nhân lùi vô hạn có thể được sử dụng để tính diện tích của các hình fractal hoặc thể tích của các vật thể có cấu trúc lặp lại.
• Phân tích tín hiệu: Trong kỹ thuật, CT cấp số nhân lùi vô hạn được sử dụng để phân tích và xử lý tín hiệu.

Ví dụ: Biểu diễn số thập phân vô hạn tuần hoàn 0.777… dưới dạng phân số.

0. 777… = 0.7 + 0.07 + 0.007 + … = 7/10 + 7/10² + 7/10³ + …

Đây là tổng của CT cấp số nhân lùi vô hạn với u₁ = 7/10 và q = 1/10.

S = (7/10) / (1 – 1/10) = (7/10) / (9/10) = 7/9

Vậy 0.777… = 7/9

6. Bài Tập CT Cấp Số Nhân và Phương Pháp Giải Chi Tiết: Luyện Tập Để Thành Thạo

Để nắm vững kiến thức về CT cấp số nhân, việc luyện tập giải các bài tập là vô cùng quan trọng. Dưới đây là một số bài tập điển hình và phương pháp giải chi tiết.

Câu 1: Cho CT cấp số nhân (u_n) có công bội q.

a) Biết u₁ = 2, u₆ = 486. Tìm q.

b) Biết q = 2/3, u₄ = 8/21. Tính u₁.

c) Biết u₁ = 3, q = -2. Xác định số 192 là số hạng thứ mấy trong CT cấp số nhân?

Lời giải:

Áp dụng công thức u_n = u₁ * q^n-1

a) u₆ = u₁ * q⁵ => q⁵ = u₆ / u₁ = 486 / 2 = 243 => q = 3

b) u₄ = u₁ * q³ => u₁ = u₄ / q³ = (8/21) / (2/3)³ = 9/7

c) 192 = 3 * (-2)^n-1 => (-2)^n-1 = 64 => n – 1 = 6 => n = 7

Vậy số 192 là số hạng thứ 7.

Câu 2: Tìm các số hạng của CT cấp số nhân (u_n) biết CT cấp số nhân gồm có 5 số hạng và:

a) u₃ = 3, u₅ = 27

b) u₄ – u₂ = 25, u₃ – u₁ = 50

Lời giải:

a) u₃ = u₁ q² => 3 = u₁ q² (1)

u₅ = u₁ q⁴ => 27 = u₁ q⁴ (2)

Từ (1) và (2) => q² = (u₁ q⁴) / (u₁ q²) = 9 => q = ±3

• Với q = 3 => u₁ = 1/3. CT cấp số nhân là: 1/3, 1, 3, 9, 27
• Với q = -3 => u₁ = -1/3. CT cấp số nhân là: -1/3, 1, -3, 9, -27

b) u₄ – u₂ = 25 => u₁q³ – u₁q = 25 (1)

u₃ – u₁ = 50 => u₁q² – u₁ = 50 (2)

Từ (1) và (2) => u₁q(q² – 1) = 25

u₁(q² – 1) = 50

=> q = 1/2 => u₁ = -200/3

Vậy CT cấp số nhân là: -200/3, -100/3, -50/3, -25/3, -25/6

Câu 3: Tìm CT cấp số nhân có sáu số hạng, biết rằng tổng của 5 số hạng đầu là 31 và tổng của 5 số hạng sau là 62.

Lời giải:

u₁ + u₂ + u₃ + u₄ + u₅ = 31

=> u₁q + u₂q + u₃q + u₄q + u₅q = 31q

=> u₂ + u₃ + u₄ + u₅ + u₆ = 31q (1)

u₂ + u₃ + u₄ + u₅ + u₆ = 62 (2)

Từ (1) và (2) => 31q = 62 => q = 2

Vì S₅ = 31 = u₁(1 – 2⁵) / (1 – 2) => u₁ = 1

Vậy CT cấp số nhân là: 1, 2, 4, 8, 16, 32

7. Ứng Dụng Thực Tế Của CT Cấp Số Nhân: Không Chỉ Là Toán Học

CT cấp số nhân không chỉ là một khái niệm trừu tượng trong toán học, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau. Dưới đây là một số ví dụ điển hình:

• Tính lãi kép: Lãi kép là một hình thức tính lãi mà tiền lãi được cộng vào vốn gốc để tạo ra một vốn gốc mới cho kỳ tính lãi tiếp theo. CT cấp số nhân được sử dụng để tính số tiền lãi và vốn gốc sau một khoảng thời gian nhất định.
• Tăng trưởng dân số: CT cấp số nhân có thể được sử dụng để dự báo tăng trưởng dân số dựa trên tỷ lệ tăng trưởng hàng năm.
• Giá trị khấu hao tài sản: CT cấp số nhân được sử dụng để tính giá trị còn lại của một tài sản sau một khoảng thời gian sử dụng, dựa trên tỷ lệ khấu hao hàng năm.
• Phân tích tài chính: CT cấp số nhân được sử dụng để phân tích các chuỗi số trong tài chính, chẳng hạn như dòng tiền, doanh thu, và lợi nhuận.
• Khoa học máy tính: CT cấp số nhân được sử dụng trong các thuật toán tìm kiếm và sắp xếp dữ liệu.

Ví dụ: Tỉ lệ tăng dân số của một tỉnh là 1.4%. Biết rằng hiện tại số dân của tỉnh là 1.8 triệu người. Hỏi sau 5 năm và 10 năm nữa, số dân của tỉnh là bao nhiêu?

Gọi số dân hiện tại của tỉnh là N = 1.8 triệu người.

Sau một năm, dân số tăng thêm 1.4%N, vậy số dân năm sau là N + 1.4%N = 1.014N.

Số dân của tỉnh sau mỗi năm lập thành một CT cấp số nhân: N, (1.014)N, (1.014)²N,…

• Sau 5 năm, số dân của tỉnh là (1.014)⁵ * 1.8 ≈ 1.9 triệu người.
• Sau 10 năm, số dân của tỉnh là (1.014)¹⁰ * 1.8 ≈ 2.1 triệu người.

8. Mẹo Hay Ghi Nhớ Công Thức CT Cấp Số Nhân: Học Dễ, Nhớ Lâu

Ghi nhớ các công thức CT cấp số nhân có thể là một thách thức đối với nhiều người. Tuy nhiên, có một số mẹo hay giúp bạn học dễ hơn và nhớ lâu hơn:

• Hiểu rõ bản chất: Thay vì học thuộc lòng, hãy cố gắng hiểu rõ bản chất của từng công thức. Ví dụ, công thức số hạng tổng quát u_n = u₁ * q^n-1 cho thấy rằng mỗi số hạng trong CT cấp số nhân được tạo ra bằng cách nhân số hạng đầu tiên với công bội (n-1) lần.
• Liên hệ với thực tế: Tìm các ví dụ thực tế để liên hệ với các công thức. Ví dụ, lãi kép là một ứng dụng tuyệt vời để minh họa cho CT cấp số nhân.
• Sử dụng sơ đồ tư duy: Vẽ sơ đồ tư duy để hệ thống hóa các công thức và mối liên hệ giữa chúng.
• Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các công thức và cách áp dụng chúng.
• Tạo ra các câu chuyện hoặc hình ảnh hài hước: Sử dụng các câu chuyện hoặc hình ảnh hài hước để liên kết với các công thức. Ví dụ, bạn có thể tưởng tượng một con thỏ (u₁) đang sinh sản theo cấp số nhân (q) để nhớ công thức số hạng tổng quát.

9. Tài Liệu Tham Khảo CT Cấp Số Nhân Tại tic.edu.vn: Học Mọi Lúc, Mọi Nơi

Tại tic.edu.vn, chúng tôi cung cấp một nguồn tài liệu phong phú và đa dạng về CT cấp số nhân, bao gồm:

• Bài giảng chi tiết: Các bài giảng được trình bày một cách rõ ràng, dễ hiểu, với nhiều ví dụ minh họa và bài tập thực hành.
• Bài tập tự luyện: Các bài tập được chia thành nhiều mức độ khó khác nhau, giúp bạn luyện tập và nâng cao kỹ năng giải toán.
• Đề thi thử: Các đề thi thử được biên soạn theo cấu trúc đề thi THPT quốc gia, giúp bạn làm quen với hình thức thi và đánh giá năng lực của mình.
• Công cụ hỗ trợ: Các công cụ tính toán trực tuyến giúp bạn kiểm tra kết quả và tiết kiệm thời gian làm bài.
• Diễn đàn trao đổi: Diễn đàn là nơi bạn có thể đặt câu hỏi, thảo luận với các bạn học khác và nhận được sự hỗ trợ từ đội ngũ giáo viên của tic.edu.vn.

Chúng tôi cam kết cung cấp cho bạn những tài liệu chất lượng nhất, được cập nhật thường xuyên và phù hợp với chương trình học mới nhất.

10. FAQ: Giải Đáp Thắc Mắc Về CT Cấp Số Nhân

Dưới đây là một số câu hỏi thường gặp về CT cấp số nhân, cùng với câu trả lời chi tiết:

1. CT cấp số nhân là gì?

   CT cấp số nhân là một dãy số, hữu hạn hoặc vô hạn, trong đó mỗi số hạng, kể từ số hạng thứ hai, đều bằng tích của số hạng đứng ngay trước nó với một số không đổi (công bội).

2. Công bội q của CT cấp số nhân là gì?

   Công bội q là số không đổi mà mỗi số hạng trong CT cấp số nhân được nhân với để tạo ra số hạng tiếp theo.

3. Làm thế nào để xác định một dãy số có phải là CT cấp số nhân hay không?

   Tính tỉ số giữa hai số hạng liên tiếp bất kỳ trong dãy số. Nếu tỉ số này là một hằng số (không đổi), thì dãy số đó là CT cấp số nhân.

4. Công thức số hạng tổng quát của CT cấp số nhân là gì?

   u_n = u₁ * q^n-1, trong đó u_n là số hạng thứ n, u₁ là số hạng đầu tiên và q là công bội.

5. Công thức tính tổng n số hạng đầu tiên của CT cấp số nhân là gì?

   S_n = u₁ * (1 – qⁿ) / (1 – q) (nếu q ≠ 1)

   S_n = n * u₁ (nếu q = 1)

6. CT cấp số nhân lùi vô hạn là gì?

   CT cấp số nhân lùi vô hạn là CT cấp số nhân có công bội q thỏa mãn điều kiện -1 < q < 1.

7. Công thức tính tổng của CT cấp số nhân lùi vô hạn là gì?

   S = u₁ / (1 – q)

8. CT cấp số nhân có những ứng dụng thực tế nào?

   CT cấp số nhân có nhiều ứng dụng trong các lĩnh vực như tính lãi kép, tăng trưởng dân số, giá trị khấu hao tài sản, phân tích tài chính, khoa học máy tính,…

9. Tôi có thể tìm thêm tài liệu về CT cấp số nhân ở đâu?

   Bạn có thể tìm thêm tài liệu về CT cấp số nhân tại tic.edu.vn, bao gồm bài giảng chi tiết, bài tập tự luyện, đề thi thử, công cụ hỗ trợ và diễn đàn trao đổi.

10. Làm thế nào để ghi nhớ các công thức CT cấp số nhân một cách hiệu quả?

    Hiểu rõ bản chất, liên hệ với thực tế, sử dụng sơ đồ tư duy, luyện tập thường xuyên và tạo ra các câu chuyện hoặc hình ảnh hài hước.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin, hoặc cần công cụ hỗ trợ học tập hiệu quả? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, đa dạng, được kiểm duyệt kỹ lưỡng, cùng với các công cụ hỗ trợ học tập trực tuyến và cộng đồng học tập sôi nổi. Đừng bỏ lỡ cơ hội nâng cao kiến thức và kỹ năng của bạn! Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để biết thêm chi tiết.

Nội dung được cung cấp trên trang web tic.edu.vn chỉ mang tính chất tham khảo và không thay thế cho lời khuyên chuyên môn từ các chuyên gia giáo dục hoặc cố vấn tài chính. Việc áp dụng các kiến thức và công cụ được cung cấp trên trang web vào thực tế cần được thực hiện một cách cẩn trọng và có sự cân nhắc kỹ lưỡng.

Bài viết này đã cung cấp một cái nhìn tổng quan về CT cấp số nhân, từ định nghĩa, tính chất, công thức, đến ứng dụng thực tế và các mẹo học tập hiệu quả. Hy vọng rằng bài viết này sẽ giúp bạn nắm vững kiến thức về CT cấp số nhân và đạt được thành công trong học tập và công việc.