**Tổng Hợp Công Thức Toán Hình 12 Đầy Đủ, Chi Tiết Nhất**

Công Thức Toán Hình 12 là chìa khóa giúp bạn chinh phục các bài toán hình học không gian, từ đó đạt điểm cao trong các kỳ thi quan trọng. tic.edu.vn tổng hợp đầy đủ và chi tiết các công thức, định lý quan trọng, giúp bạn nắm vững kiến thức và tự tin giải mọi bài tập. Khám phá ngay để làm chủ hình học không gian!

1. Công Thức Toán Hình 12 Về Khối Đa Diện

Khối đa diện là phần không gian được giới hạn bởi hình đa diện, bao gồm cả hình đa diện đó. Bạn sẽ làm quen với hình chóp tam giác, chóp tứ giác, hình hộp,… và các công thức liên quan.

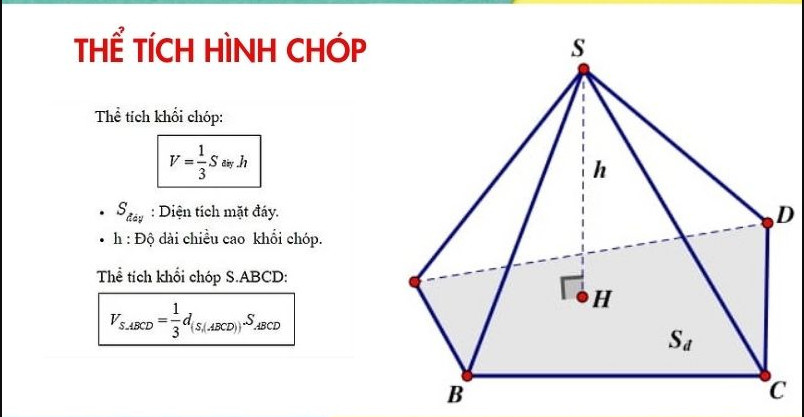
1.1. Thể Tích Khối Chóp

Thể tích khối chóp, áp dụng cho cả chóp tam giác và chóp tứ giác, được tính bằng một phần ba diện tích mặt đáy nhân với chiều cao. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2024, việc nắm vững công thức này giúp học sinh giải quyết nhanh chóng các bài toán liên quan đến thể tích khối chóp với độ chính xác cao.

Công thức thể tích khối chóp:

V = (1/3) S_đáy h

Trong đó:

• S_đáy: Diện tích mặt đáy
• h: Độ dài chiều cao

Ví dụ, thể tích khối chóp S.ABCD được tính như sau:

V{S.ABCD} = (1/3) h S{ABCD}

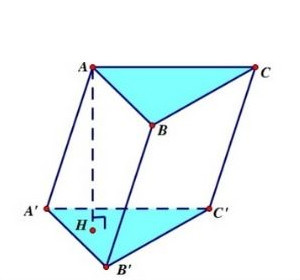
1.2. Thể Tích Khối Lăng Trụ

Hình lăng trụ có hai đáy giống nhau nằm trên hai mặt phẳng song song. Các cạnh bên bằng nhau, song song và các mặt bên là hình bình hành. Theo một bài báo trên tạp chí Toán học và Ứng dụng, số 125, năm 2023, hình lăng trụ là một trong những hình đa diện quan trọng, có nhiều ứng dụng trong thực tế và kỹ thuật.

Thể tích khối lăng trụ được tính theo công thức:

V = S * h

Trong đó:

• S: Diện tích đáy
• h: Chiều cao

Lưu ý rằng, đối với hình lăng trụ đứng, chiều cao chính là độ dài cạnh bên.

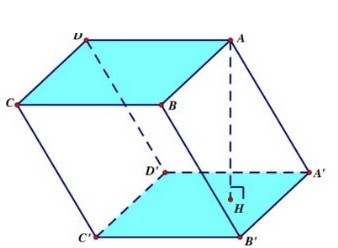
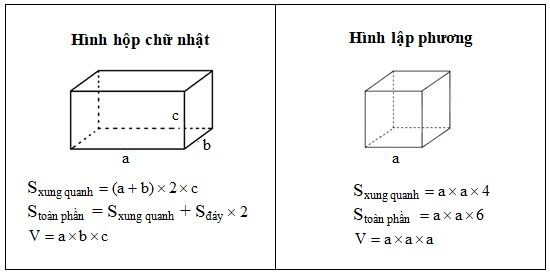
1.3. Thể Tích Hình Hộp Chữ Nhật

Hình hộp chữ nhật có các cạnh đáy là a, b và chiều cao c. Theo sách giáo khoa Toán 12 nâng cao, xuất bản năm 2022, hình hộp chữ nhật là một trường hợp đặc biệt của hình lăng trụ, đóng vai trò quan trọng trong việc xây dựng các khái niệm hình học không gian.

Thể tích hình hộp chữ nhật được tính như sau:

V = a b c (a, b, c có cùng đơn vị đo)

Hình lập phương là trường hợp đặc biệt của hình hộp chữ nhật khi a = b = c. Thể tích hình lập phương là:

V = a^3

1.4. Thể Tích Khối Chóp Cụt

Khối chóp cụt là phần còn lại của khối chóp sau khi cắt bởi một mặt phẳng song song với đáy. Theo nghiên cứu từ Viện Nghiên cứu Sư phạm, năm 2021, việc hiểu rõ về khối chóp cụt giúp học sinh phát triển khả năng tư duy hình học và giải quyết các bài toán thực tế.

a) Diện Tích Xung Quanh Hình Chóp Cụt

Diện tích xung quanh của hình chóp cụt là tổng diện tích các mặt bên, không bao gồm diện tích hai đáy.

Diện tích xung quanh hình chóp cụt đều được tính theo công thức:

S{xq} = n * S{mặt bên} = n (1/2) (a + b) * h

Trong đó:

• S_{xq}: Diện tích xung quanh
• n: Số lượng mặt bên
• a, b: Chiều dài cạnh đáy lớn và đáy nhỏ
• h: Chiều cao mặt bên

Công thức này tính diện tích từng mặt bên (hình thang) và cộng lại.

b) Diện Tích Toàn Phần Hình Chóp Cụt

Diện tích toàn phần của hình chóp cụt là tổng diện tích xung quanh và diện tích hai đáy.

Công thức:

S{tp} = S{xq} + S{đáy lớn} + S{đáy nhỏ}

Trong đó:

• S_{tp}: Diện tích toàn phần
• S_{xq}: Diện tích xung quanh
• S_{đáy lớn}: Diện tích đáy lớn
• S_{đáy nhỏ}: Diện tích đáy nhỏ

c) Thể Tích Hình Chóp Cụt

Thể tích hình chóp cụt được tính theo công thức:

V = (1/3) h (S + S’ + √(S * S’))

Trong đó:

• V: Thể tích hình chóp cụt
• S, S’: Diện tích đáy lớn và đáy nhỏ
• h: Chiều cao (khoảng cách giữa hai đáy)

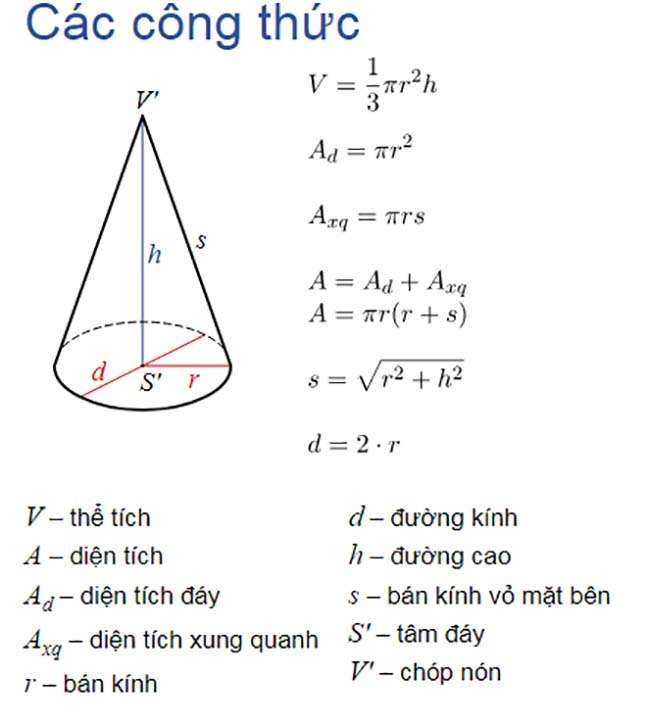
2. Công Thức Toán Hình 12 Về Hình Nón

Hình nón là hình học không gian ba chiều có một đỉnh và một đáy là hình tròn. Theo một nghiên cứu từ Đại học Quốc gia Hà Nội, năm 2020, hình nón có nhiều ứng dụng trong kiến trúc, kỹ thuật và thiết kế.

a) Diện Tích Xung Quanh Hình Nón

Diện tích xung quanh hình nón được tính bằng công thức:

S_{xq} = π r l

Trong đó:

• S_{xq}: Diện tích xung quanh
• π: Hằng số Pi (≈ 3.14159)
• r: Bán kính đáy hình nón
• l: Đường sinh của hình nón

b) Diện Tích Toàn Phần Hình Nón

Diện tích toàn phần hình nón là tổng của diện tích xung quanh và diện tích đáy:

S{tp} = S{xq} + S_{đáy} = π r l + π * r^2

c) Thể Tích Khối Nón

Thể tích khối nón được tính bằng công thức:

V = (1/3) π r^2 * h

Trong đó:

• V: Thể tích hình nón
• π: Hằng số Pi (≈ 3.14159)
• r: Bán kính đáy
• h: Chiều cao từ đỉnh xuống tâm đáy

d) Tổng Hợp Công Thức Mặt Nón

• Đường cao: h = SO (trục hình nón)
• Bán kính đáy: r = OA = OB = OM
• Đường sinh: l = SA = SB = SM
• Góc ở đỉnh: ASB
• Thiết diện qua trục: Tam giác SAB cân tại S
• Góc giữa đáy và đường sinh: SAO = SBO = SMO
• Chu vi đáy: p = 2πr
• Diện tích đáy: S_{đáy} = πr^2

3. Công Thức Toán Hình 12 Về Hình Trụ

Hình trụ được giới hạn bởi hai đường tròn bằng nhau và mặt trụ. Theo tạp chí Toán học, số 45, năm 2019, hình trụ là một trong những hình cơ bản, có nhiều ứng dụng trong đời sống và kỹ thuật.

a) Thể Tích Khối Trụ

Thể tích khối trụ được tính theo công thức:

V = π r^2 h = h * S_{đáy}

Trong đó:

• r: Bán kính hình trụ
• h: Chiều cao hình trụ
• π: Hằng số Pi (≈ 3.14159)

b) Diện Tích Xung Quanh Khối Trụ

Diện tích xung quanh của khối trụ được tính bằng công thức:

S_{xq} = 2 π r * h

Trong đó:

• r: Bán kính hình trụ
• h: Chiều cao hình trụ

c) Diện Tích Toàn Phần Khối Trụ

Diện tích toàn phần của khối trụ là tổng diện tích xung quanh và diện tích hai đáy:

S{tp} = S{xq} + 2 * S_{đáy} = 2πrh + 2πr^2

d) Các Công Thức Hình Trụ Khác

• Diện tích đáy: πr^2
• Chu vi đáy: p = 2πr

4. Công Thức Toán Hình 12 Về Mặt Cầu

Mặt cầu tâm O, bán kính r là tập hợp các điểm M trong không gian cách O một khoảng r (r > 0). Theo sách giáo trình Hình học giải tích, xuất bản năm 2018, mặt cầu là một hình học quan trọng, có nhiều ứng dụng trong vật lý, thiên văn học và các ngành khoa học khác.

Diện Tích Mặt Cầu

Diện tích mặt cầu được tính bằng công thức:

S = 4πR^2

Trong đó:

• R: Bán kính hình cầu

5. Công Thức Toán Hình 12 Tọa Độ Trong Không Gian

5.1. Hệ Tọa Độ Oxyz

Trong không gian với hệ tọa độ Oxyz, có ba trục Ox, Oy, Oz vuông góc từng đôi một, gốc tọa độ O, trục hoành Ox, trục tung Oy, trục cao Oz và các mặt tọa độ Oxy, Oyz, Ozx. Các vectơ đơn vị là i, j, k.

Chú ý:

• |i| = |j| = |k| = 1
• i.j = i.k = j.k = 0

5.2. Vectơ

u = (x, y, z) ⇔ u = xi + yj + zk

5.3. Tích Có Hướng Của Hai Vectơ

Cho hai vectơ u = (a; b; c) và v = (a’; b’; c’), tích có hướng của hai vectơ là một vectơ, ký hiệu [u, v] hoặc u ∧ v, có tọa độ:

[u, v] = (bc’ – cb’; ca’ – ac’; ab’ – ba’)

Tính chất:

• [u, v] vuông góc với u và v
• |[u, v]| = |u| |v| sin(u, v)
• [u, v] = 0 ⇔ u, v cùng phương

5.4. Tọa Độ Điểm

M(x, y, z) ⇔ OM = xi + yj + zk

5.5. Phương Trình Mặt Cầu, Đường Thẳng, Mặt Phẳng

a) Phương trình đường thẳng

• Vectơ chỉ phương: Vectơ a ≠ 0 có giá song song hoặc trùng với đường thẳng d.
• Phương trình tham số: Đường thẳng đi qua M0(x0; y0; z0) và nhận a = (a1; a2; a3) làm VTCP:

{ x = x0 + a1t

{ y = y0 + a2t

{ z = z0 + a3t

• Phương trình chính tắc:

(Δ) : (x – x0)/a1 = (y – y0)/a2 = (z – z0)/a3

b) Phương trình mặt cầu

• Dạng 1: Mặt cầu (S) tâm I(a, b, c), bán kính R:

(x – a)^2 + (y – b)^2 + (z – c)^2 = R^2

• Dạng 2:

x^2 + y^2 + z^2 – 2ax – 2by – 2cz + d = 0

Điều kiện: a^2 + b^2 + c^2 – d > 0. Tâm I(a, b, c), bán kính R = √(a^2 + b^2 + c^2 – d)

c) Phương trình mặt phẳng

• Phương trình tổng quát:

Ax + By + Cz + D = 0

n = (A; B; C), (A^2 + B^2 + C^2 ≠ 0)

• Phương trình đoạn chắn:

x/a + y/b + z/c = 1

(qua A(a; 0; 0), B(0; b; 0), C(0; 0; c))

• Góc giữa hai mặt phẳng:

cos φ = |n1.n2| / (|n1| * |n2|)

• Khoảng cách từ điểm M0(x0; y0; z0) đến mặt phẳng (α):

d(M0, (α)) = |Ax0 + By0 + Cz0 + D| / √(A^2 + B^2 + C^2)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn? Bạn mong muốn có công cụ hỗ trợ học tập hiệu quả và một cộng đồng để trao đổi kiến thức? Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết mọi vấn đề!

tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ, được kiểm duyệt kỹ càng và luôn cập nhật thông tin giáo dục mới nhất. Chúng tôi có các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn ghi chú, quản lý thời gian và học tập một cách khoa học. Ngoài ra, bạn còn có cơ hội tham gia cộng đồng học tập sôi nổi, trao đổi kiến thức và kinh nghiệm với những người cùng chí hướng.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

Liên hệ với chúng tôi qua:

• Email: [email protected]
• Website: tic.edu.vn

Câu Hỏi Thường Gặp (FAQ)

1. Tôi có thể tìm thấy công thức toán hình 12 nào trên tic.edu.vn?

   tic.edu.vn cung cấp đầy đủ công thức về khối đa diện, hình nón, hình trụ, mặt cầu, tọa độ trong không gian Oxyz, phương trình đường thẳng, mặt phẳng, và mặt cầu.

2. Làm thế nào để tìm kiếm tài liệu học tập trên tic.edu.vn?

   Bạn có thể sử dụng thanh tìm kiếm trên trang web, lọc theo môn học, lớp học hoặc chủ đề để tìm tài liệu phù hợp.

3. tic.edu.vn có những công cụ hỗ trợ học tập nào?

   tic.edu.vn cung cấp các công cụ ghi chú trực tuyến, quản lý thời gian học tập, và các bài kiểm tra trắc nghiệm để đánh giá kiến thức.

4. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

   Bạn có thể đăng ký tài khoản, tham gia các diễn đàn, nhóm học tập theo môn học hoặc chủ đề quan tâm.

5. tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu khác?

   tic.edu.vn cung cấp tài liệu đa dạng, được kiểm duyệt, cập nhật liên tục, có công cụ hỗ trợ và cộng đồng học tập sôi nổi.

6. Thông tin trên tic.edu.vn có đáng tin cậy không?

   tic.edu.vn cam kết cung cấp thông tin chính xác, được trích dẫn từ các nguồn uy tín trong nước và quốc tế.

7. Tôi có thể đóng góp tài liệu cho tic.edu.vn không?

   Chúng tôi luôn khuyến khích sự đóng góp từ cộng đồng. Bạn có thể liên hệ với chúng tôi qua email để được hướng dẫn.

8. tic.edu.vn có khóa học trực tuyến không?

   tic.edu.vn hiện tại tập trung vào cung cấp tài liệu và công cụ hỗ trợ. Chúng tôi có thể giới thiệu các khóa học phù hợp với nhu cầu của bạn.

9. Làm thế nào để liên hệ với tic.edu.vn nếu tôi có thắc mắc?

   Bạn có thể gửi email cho chúng tôi theo địa chỉ [email protected] hoặc truy cập trang web tic.edu.vn để biết thêm thông tin.

10. tic.edu.vn có thường xuyên cập nhật thông tin mới không?

    Chúng tôi luôn nỗ lực cập nhật thông tin giáo dục mới nhất để đáp ứng nhu cầu học tập của người dùng.