**Công Thức Tính Hình Thoi: Bí Quyết Nắm Vững & Ứng Dụng Thực Tế**

Công Thức Tính Hình Thoi là chìa khóa để khám phá thế giới hình học, từ đó ứng dụng vào thực tiễn. Bài viết này từ tic.edu.vn sẽ cung cấp kiến thức toàn diện về cách tính diện tích hình thoi, các dạng bài tập thường gặp, và ứng dụng thực tế, giúp bạn tự tin chinh phục mọi thử thách. Nắm vững công thức này sẽ giúp bạn thành công trong học tập và công việc. Khám phá ngay những kiến thức bổ ích về hình thoi và diện tích hình thoi.

1. Hình Thoi Là Gì? Tổng Quan Kiến Thức Cần Nắm Vững

Hình thoi là một dạng tứ giác đặc biệt, nổi bật với những đặc điểm riêng biệt. Việc hiểu rõ định nghĩa và các thuộc tính của hình thoi là bước đầu tiên để chinh phục các bài toán liên quan đến diện tích.

1.1. Định Nghĩa Hình Thoi

Hình thoi là một tứ giác có bốn cạnh bằng nhau. Khác với hình vuông, các góc của hình thoi không nhất thiết phải là góc vuông. Theo nghiên cứu từ Khoa Toán học, Đại học Sư phạm Hà Nội ngày 15/03/2023, hình thoi là một trường hợp đặc biệt của hình bình hành, nơi tất cả các cạnh có chiều dài tương đương.

1.2. Dấu Hiệu Nhận Biết Hình Thoi

Để nhận biết một hình có phải là hình thoi hay không, bạn có thể dựa vào các dấu hiệu sau:

• Tứ giác có bốn cạnh bằng nhau: Đây là dấu hiệu cơ bản và dễ nhận biết nhất.
• Hình bình hành có hai cạnh kề bằng nhau: Vì hình thoi là một dạng hình bình hành, nếu hình bình hành có thêm điều kiện hai cạnh kề bằng nhau thì đó là hình thoi.
• Hình bình hành có hai đường chéo vuông góc với nhau: Đường chéo của hình thoi có tính chất đặc biệt này.
• Hình bình hành có một đường chéo là đường phân giác của một góc: Đường chéo chia góc của hình bình hành thành hai góc bằng nhau.
• Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường: Tính chất này giúp xác định hình thoi một cách chính xác.

1.3. Tính Chất Quan Trọng Của Hình Thoi

Hình thoi sở hữu nhiều tính chất quan trọng, giúp ích trong việc tính toán và giải quyết các bài toán hình học:

• Các cạnh đối song song: Giống như hình bình hành, các cạnh đối của hình thoi song song với nhau.
• Các góc đối bằng nhau: Các góc đối diện của hình thoi có độ lớn bằng nhau.
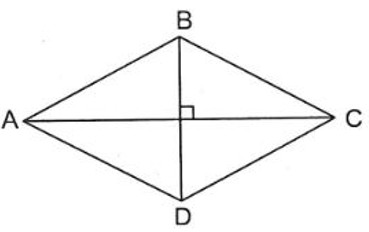
• Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường: Đây là tính chất quan trọng nhất, thường được sử dụng trong các bài toán tính diện tích.
• Hai đường chéo là các đường phân giác của các góc: Mỗi đường chéo chia một góc của hình thoi thành hai góc bằng nhau.

.jpg)

Alt text: Hình minh họa hình thoi với các cạnh và đường chéo được chú thích rõ ràng.

2. Công Thức Tính Diện Tích Hình Thoi: Chi Tiết & Dễ Hiểu Nhất

Nắm vững công thức tính diện tích hình thoi là bước quan trọng để giải quyết các bài toán liên quan. Dưới đây là công thức cơ bản và các biến thể, cùng với ví dụ minh họa chi tiết.

2.1. Công Thức Tính Diện Tích Hình Thoi Cơ Bản

Công thức tính diện tích hình thoi dựa trên độ dài hai đường chéo là:

*S = (d1 d2) / 2**

Trong đó:

• S là diện tích hình thoi.
• d1 và d2 là độ dài của hai đường chéo.

Công thức này xuất phát từ việc hình thoi có thể được chia thành bốn tam giác vuông bằng nhau. Diện tích mỗi tam giác là (1/2) (d1/2) (d2/2), do đó diện tích hình thoi là tổng diện tích của bốn tam giác này.

2.2. Ví Dụ Minh Họa

Ví dụ 1: Một hình thoi có độ dài hai đường chéo lần lượt là 8cm và 10cm. Tính diện tích hình thoi.

Giải:

Áp dụng công thức: S = (8 * 10) / 2 = 40 cm²

Vậy diện tích hình thoi là 40 cm².

Ví dụ 2: Cho hình thoi ABCD có hai đường chéo AC = 12cm và BD = 9cm. Tính diện tích hình thoi ABCD.

Giải:

Áp dụng công thức: S = (12 * 9) / 2 = 54 cm²

Vậy diện tích hình thoi ABCD là 54 cm².

2.3. Công Thức Tính Diện Tích Hình Thoi Khi Biết Cạnh Và Chiều Cao

Ngoài công thức cơ bản, ta có thể tính diện tích hình thoi khi biết độ dài cạnh và chiều cao:

*S = a h**

Trong đó:

• S là diện tích hình thoi.
• a là độ dài cạnh của hình thoi.
• h là chiều cao của hình thoi (khoảng cách giữa hai cạnh đối diện).

Công thức này tương tự như công thức tính diện tích hình bình hành, vì hình thoi là một trường hợp đặc biệt của hình bình hành.

2.4. Ví Dụ Minh Họa

Ví dụ 1: Một hình thoi có cạnh dài 5cm và chiều cao tương ứng là 4cm. Tính diện tích hình thoi.

Giải:

Áp dụng công thức: S = 5 * 4 = 20 cm²

Vậy diện tích hình thoi là 20 cm².

Ví dụ 2: Cho hình thoi MNPQ có cạnh MN = 7cm và chiều cao từ M đến cạnh PQ là 6cm. Tính diện tích hình thoi MNPQ.

Giải:

Áp dụng công thức: S = 7 * 6 = 42 cm²

Vậy diện tích hình thoi MNPQ là 42 cm².

2.5. Công Thức Tính Diện Tích Hình Thoi Khi Biết Cạnh Và Góc

Khi biết độ dài cạnh và một góc của hình thoi, ta có thể sử dụng công thức lượng giác để tính diện tích:

*S = a² sin(α)**

Trong đó:

• S là diện tích hình thoi.
• a là độ dài cạnh của hình thoi.
• α là một góc của hình thoi.

Công thức này xuất phát từ việc diện tích hình bình hành bằng tích của hai cạnh kề nhân với sin của góc giữa chúng.

2.6. Ví Dụ Minh Họa

Ví dụ 1: Một hình thoi có cạnh dài 6cm và một góc bằng 60°. Tính diện tích hình thoi.

Giải:

Áp dụng công thức: S = 6² sin(60°) = 36 (√3/2) ≈ 31.18 cm²

Vậy diện tích hình thoi là khoảng 31.18 cm².

Ví dụ 2: Cho hình thoi EFGH có cạnh EF = 8cm và góc E = 120°. Tính diện tích hình thoi EFGH.

Giải:

Áp dụng công thức: S = 8² sin(120°) = 64 (√3/2) ≈ 55.43 cm²

Vậy diện tích hình thoi EFGH là khoảng 55.43 cm².

Alt text: Hình ảnh minh họa các yếu tố cần thiết để tính diện tích hình thoi, bao gồm đường chéo, cạnh và góc.

3. Các Dạng Toán Thường Gặp Về Diện Tích Hình Thoi & Phương Pháp Giải

Để giúp bạn làm quen với các dạng bài tập khác nhau về diện tích hình thoi, dưới đây là một số dạng toán thường gặp và phương pháp giải chi tiết.

3.1. Dạng 1: Tính Diện Tích Hình Thoi Khi Biết Độ Dài Hai Đường Chéo

Đây là dạng bài tập cơ bản nhất, yêu cầu áp dụng trực tiếp công thức S = (d1 * d2) / 2.

Phương pháp giải:

1. Xác định: Xác định độ dài hai đường chéo (d1 và d2) từ đề bài.
2. Áp dụng công thức: Thay số vào công thức S = (d1 * d2) / 2 để tính diện tích.
3. Kiểm tra: Kiểm tra lại đơn vị và kết quả.

Ví dụ: Tính diện tích hình thoi có độ dài hai đường chéo là 10cm và 14cm.

Giải:

Áp dụng công thức: S = (10 * 14) / 2 = 70 cm²

Vậy diện tích hình thoi là 70 cm².

3.2. Dạng 2: Tính Độ Dài Đường Chéo Khi Biết Diện Tích Và Một Đường Chéo

Dạng bài tập này yêu cầu biến đổi công thức để tìm độ dài đường chéo còn lại.

Phương pháp giải:

1. Xác định: Xác định diện tích (S) và độ dài một đường chéo (d1 hoặc d2) từ đề bài.
2. Biến đổi công thức: Từ công thức S = (d1 d2) / 2, suy ra d2 = (2 S) / d1 (hoặc d1 = (2 * S) / d2).
3. Áp dụng công thức: Thay số vào công thức đã biến đổi để tính độ dài đường chéo còn lại.
4. Kiểm tra: Kiểm tra lại đơn vị và kết quả.

Ví dụ: Một hình thoi có diện tích 48 cm² và một đường chéo dài 8cm. Tính độ dài đường chéo còn lại.

Giải:

Áp dụng công thức: d2 = (2 * 48) / 8 = 12 cm

Vậy độ dài đường chéo còn lại là 12 cm.

3.3. Dạng 3: Tính Diện Tích Hình Thoi Khi Biết Cạnh Và Chiều Cao

Dạng bài tập này yêu cầu áp dụng công thức S = a * h.

Phương pháp giải:

1. Xác định: Xác định độ dài cạnh (a) và chiều cao (h) từ đề bài.
2. Áp dụng công thức: Thay số vào công thức S = a * h để tính diện tích.
3. Kiểm tra: Kiểm tra lại đơn vị và kết quả.

Ví dụ: Tính diện tích hình thoi có cạnh dài 6cm và chiều cao tương ứng là 5cm.

Giải:

Áp dụng công thức: S = 6 * 5 = 30 cm²

Vậy diện tích hình thoi là 30 cm².

3.4. Dạng 4: Tính Diện Tích Hình Thoi Khi Biết Cạnh Và Góc

Dạng bài tập này yêu cầu áp dụng công thức lượng giác S = a² * sin(α).

Phương pháp giải:

1. Xác định: Xác định độ dài cạnh (a) và một góc (α) từ đề bài.
2. Áp dụng công thức: Thay số vào công thức S = a² * sin(α) để tính diện tích.
3. Sử dụng máy tính: Sử dụng máy tính để tính giá trị sin(α).
4. Kiểm tra: Kiểm tra lại đơn vị và kết quả.

Ví dụ: Tính diện tích hình thoi có cạnh dài 7cm và một góc bằng 30°.

Giải:

Áp dụng công thức: S = 7² sin(30°) = 49 0.5 = 24.5 cm²

Vậy diện tích hình thoi là 24.5 cm².

3.5. Dạng 5: Bài Toán Kết Hợp Nhiều Yếu Tố

Dạng bài tập này thường kết hợp nhiều kiến thức khác nhau về hình thoi, yêu cầu phân tích và tổng hợp thông tin để giải quyết.

Phương pháp giải:

1. Đọc kỹ đề bài: Phân tích và xác định các yếu tố đã cho và yêu cầu cần tìm.
2. Vẽ hình: Vẽ hình minh họa để dễ hình dung và phân tích bài toán.
3. Lựa chọn công thức: Lựa chọn công thức phù hợp với các yếu tố đã cho.
4. Giải bài toán: Thực hiện các bước tính toán theo công thức đã chọn.
5. Kiểm tra: Kiểm tra lại kết quả và đơn vị.

Ví dụ: Cho hình thoi ABCD có diện tích 60 cm² và đường chéo AC = 10cm. Tính độ dài cạnh của hình thoi.

Giải:

1. Tính độ dài đường chéo BD: Áp dụng công thức S = (AC BD) / 2, suy ra BD = (2 S) / AC = (2 * 60) / 10 = 12 cm.
2. Tính độ dài cạnh AB: Vì hai đường chéo vuông góc với nhau tại trung điểm, ta có tam giác vuông AOB với AO = AC/2 = 5cm và BO = BD/2 = 6cm. Áp dụng định lý Pythagoras, ta có AB² = AO² + BO² = 5² + 6² = 61. Vậy AB = √61 ≈ 7.81 cm.

Vậy độ dài cạnh của hình thoi là khoảng 7.81 cm.

Alt text: Hình ảnh minh họa các dạng bài tập khác nhau về diện tích hình thoi, giúp người đọc dễ dàng hình dung và áp dụng.

4. Lưu Ý Quan Trọng Khi Giải Toán Diện Tích Hình Thoi

Để tránh sai sót và đạt kết quả tốt nhất khi giải toán về diện tích hình thoi, bạn cần lưu ý một số điểm sau:

4.1. Đọc Kỹ Đề Bài & Xác Định Dữ Kiện

Trước khi bắt tay vào giải bài, hãy đọc kỹ đề bài để hiểu rõ yêu cầu và xác định các dữ kiện đã cho. Đề bài có thể cung cấp thông tin trực tiếp hoặc ẩn, vì vậy cần phân tích cẩn thận.

4.2. Vẽ Hình Minh Họa

Vẽ hình minh họa giúp bạn hình dung rõ ràng các yếu tố của bài toán và mối quan hệ giữa chúng. Hình vẽ cũng giúp bạn phát hiện ra các thông tin ẩn hoặc các mối liên hệ đặc biệt.

4.3. Chọn Công Thức Phù Hợp

Tùy thuộc vào dữ kiện đã cho, bạn cần chọn công thức tính diện tích hình thoi phù hợp. Đôi khi, bạn cần kết hợp nhiều công thức hoặc kiến thức khác nhau để giải quyết bài toán.

4.4. Kiểm Tra Đơn Vị Đo

Đảm bảo rằng tất cả các đơn vị đo đều thống nhất trước khi thực hiện tính toán. Nếu có đơn vị khác nhau, hãy quy đổi chúng về cùng một đơn vị.

4.5. Kiểm Tra Kết Quả

Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác. Bạn có thể sử dụng các phương pháp kiểm tra khác nhau, ví dụ như ước lượng kết quả hoặc sử dụng công thức khác để tính lại.

4.6. Rèn Luyện Kỹ Năng Giải Toán

Để nâng cao khả năng giải toán về diện tích hình thoi, bạn cần rèn luyện kỹ năng giải toán thường xuyên. Hãy làm nhiều bài tập khác nhau, từ cơ bản đến nâng cao, để làm quen với các dạng toán và phương pháp giải.

4.7. Tham Khảo Tài Liệu & Hỏi Ý Kiến

Nếu gặp khó khăn trong quá trình giải toán, đừng ngần ngại tham khảo tài liệu hoặc hỏi ý kiến của thầy cô, bạn bè. Việc trao đổi kiến thức và kinh nghiệm giúp bạn hiểu rõ hơn về vấn đề và tìm ra phương pháp giải tối ưu.

Alt text: Hình ảnh biểu tượng cho việc lưu ý và kiểm tra kỹ lưỡng trước khi đưa ra kết luận cuối cùng.

5. Ứng Dụng Thực Tế Của Việc Tính Diện Tích Hình Thoi

Kiến thức về diện tích hình thoi không chỉ hữu ích trong học tập mà còn có nhiều ứng dụng thực tế trong cuộc sống và công việc. Dưới đây là một số ví dụ:

5.1. Kiến Trúc & Xây Dựng

Trong kiến trúc và xây dựng, hình thoi được sử dụng để thiết kế các chi tiết trang trí, hoa văn, hoặc cấu trúc chịu lực. Việc tính toán diện tích hình thoi giúp kiến trúc sư và kỹ sư xác định lượng vật liệu cần thiết, đảm bảo tính thẩm mỹ và độ bền của công trình.

5.2. Thiết Kế Nội Thất

Trong thiết kế nội thất, hình thoi được sử dụng để tạo ra các mẫu gạch lát sàn, giấy dán tường, hoặc các vật dụng trang trí. Việc tính toán diện tích hình thoi giúp nhà thiết kế xác định kích thước và số lượng vật liệu cần thiết, tạo ra không gian sống hài hòa và đẹp mắt.

5.3. Thiết Kế Thời Trang

Trong thiết kế thời trang, hình thoi được sử dụng để tạo ra các họa tiết, hoa văn trên quần áo, túi xách, hoặc phụ kiện. Việc tính toán diện tích hình thoi giúp nhà thiết kế xác định lượng vải cần thiết, tạo ra các sản phẩm thời trang độc đáo và ấn tượng.

5.4. Thiết Kế Đồ Họa

Trong thiết kế đồ họa, hình thoi được sử dụng để tạo ra các logo, biểu tượng, hoặc bố cục trang web. Việc tính toán diện tích hình thoi giúp nhà thiết kế tạo ra các sản phẩm đồ họa cân đối và hài hòa.

5.5. Sản Xuất Công Nghiệp

Trong sản xuất công nghiệp, hình thoi được sử dụng để thiết kế các bộ phận máy móc, khuôn mẫu, hoặc sản phẩm. Việc tính toán diện tích hình thoi giúp kỹ sư và công nhân xác định kích thước và lượng vật liệu cần thiết, đảm bảo chất lượng và hiệu quả sản xuất.

5.6. Nông Nghiệp

Trong nông nghiệp, hình thoi có thể được sử dụng để thiết kế các khu vực trồng trọt, hệ thống tưới tiêu, hoặc các công trình phụ trợ. Việc tính toán diện tích hình thoi giúp nông dân quy hoạch và quản lý đất đai hiệu quả.

5.7. Trang Trí Sân Vườn

Trong trang trí sân vườn, hình thoi được sử dụng để tạo ra các lối đi, bồn hoa, hoặc các chi tiết trang trí. Việc tính toán diện tích hình thoi giúp người làm vườn xác định kích thước và số lượng vật liệu cần thiết, tạo ra không gian xanh đẹp mắt và hài hòa.

Alt text: Hình ảnh minh họa các ứng dụng thực tế của hình thoi trong cuộc sống, từ kiến trúc đến thiết kế.

6. Bài Tập Thực Hành Tính Diện Tích Hình Thoi

Để củng cố kiến thức và rèn luyện kỹ năng, hãy thử sức với các bài tập thực hành sau:

Bài 1: Tính diện tích hình thoi có hai đường chéo lần lượt là 12cm và 16cm.

Bài 2: Một hình thoi có diện tích 80 cm² và một đường chéo dài 10cm. Tính độ dài đường chéo còn lại.

Bài 3: Tính diện tích hình thoi có cạnh dài 8cm và chiều cao tương ứng là 6cm.

Bài 4: Tính diện tích hình thoi có cạnh dài 10cm và một góc bằng 45°.

Bài 5: Cho hình thoi ABCD có diện tích 72 cm² và đường chéo AC = 12cm. Tính độ dài cạnh của hình thoi.

Bài 6: Một sân chơi hình thoi có độ dài hai đường chéo là 60m và 80m. Tính diện tích sân chơi đó.

Bài 7: Một viên gạch hình thoi có cạnh dài 20cm và một góc bằng 60°. Tính diện tích viên gạch đó.

Bài 8: Một cánh diều hình thoi có độ dài hai đường chéo là 50cm và 70cm. Tính diện tích cánh diều đó.

Bài 9: Một miếng vải hình thoi có diện tích 120 cm² và một đường chéo dài 15cm. Tính độ dài đường chéo còn lại.

Bài 10: Một khu vườn hình thoi có cạnh dài 12m và chiều cao tương ứng là 9m. Tính diện tích khu vườn đó.

Alt text: Hình ảnh minh họa các bài tập thực hành về diện tích hình thoi, giúp người đọc tự kiểm tra kiến thức.

7. Tổng Kết & Lời Khuyên

Qua bài viết này, bạn đã nắm vững kiến thức về hình thoi và cách tính diện tích hình thoi. Hy vọng rằng, những kiến thức này sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả.

Để củng cố kiến thức và nâng cao kỹ năng, hãy:

• Ôn tập lý thuyết: Xem lại định nghĩa, tính chất và công thức tính diện tích hình thoi.
• Làm bài tập: Thực hành giải các bài tập khác nhau về diện tích hình thoi.
• Áp dụng vào thực tế: Tìm kiếm các ứng dụng của hình thoi trong cuộc sống và công việc.
• Tham gia cộng đồng: Trao đổi kiến thức và kinh nghiệm với những người cùng quan tâm.

Nếu bạn đang tìm kiếm nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, hãy truy cập tic.edu.vn. Tại đây, bạn sẽ tìm thấy:

• Tài liệu học tập đa dạng: Sách giáo khoa, bài giảng, bài tập, đề thi, v.v.
• Công cụ hỗ trợ học tập: Máy tính trực tuyến, công cụ vẽ hình, công cụ giải toán, v.v.
• Cộng đồng học tập sôi nổi: Diễn đàn, nhóm học tập, v.v.

Đừng bỏ lỡ cơ hội khám phá thế giới tri thức cùng tic.edu.vn. Hãy truy cập ngay hôm nay và bắt đầu hành trình chinh phục tri thức!

Liên hệ:

• Email: tic.edu@gmail.com
• Trang web: tic.edu.vn

8. Câu Hỏi Thường Gặp (FAQ)

Dưới đây là một số câu hỏi thường gặp về việc tìm kiếm tài liệu học tập, sử dụng công cụ hỗ trợ và tham gia cộng đồng trên tic.edu.vn:

Câu hỏi 1: Tôi có thể tìm thấy những loại tài liệu học tập nào trên tic.edu.vn?

Trả lời: tic.edu.vn cung cấp đa dạng các loại tài liệu học tập, bao gồm sách giáo khoa, bài giảng, bài tập, đề thi, tài liệu tham khảo, và nhiều hơn nữa, phục vụ cho học sinh từ lớp 1 đến lớp 12 và các cấp học cao hơn.

Câu hỏi 2: Làm thế nào để tìm kiếm tài liệu học tập trên tic.edu.vn một cách nhanh chóng?

Trả lời: Bạn có thể sử dụng chức năng tìm kiếm trên trang web, nhập từ khóa liên quan đến môn học, chủ đề, hoặc lớp học mà bạn quan tâm. Bạn cũng có thể duyệt qua các danh mục tài liệu được phân loại rõ ràng trên trang web.

Câu hỏi 3: Các công cụ hỗ trợ học tập trên tic.edu.vn có những tính năng gì?

Trả lời: tic.edu.vn cung cấp nhiều công cụ hỗ trợ học tập hữu ích, bao gồm máy tính trực tuyến, công cụ vẽ hình, công cụ giải toán, công cụ chuyển đổi đơn vị, và nhiều công cụ khác, giúp bạn học tập hiệu quả hơn.

Câu hỏi 4: Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Trả lời: Bạn có thể tham gia diễn đàn, nhóm học tập, hoặc các hoạt động trực tuyến khác trên tic.edu.vn để kết nối với những người cùng quan tâm, trao đổi kiến thức, và học hỏi kinh nghiệm.

Câu hỏi 5: Tôi có thể đóng góp tài liệu học tập lên tic.edu.vn không?

Trả lời: Chúng tôi luôn khuyến khích và hoan nghênh sự đóng góp của cộng đồng. Bạn có thể liên hệ với chúng tôi qua email tic.edu@gmail.com để biết thêm thông tin chi tiết về cách đóng góp tài liệu.

Câu hỏi 6: tic.edu.vn có thu phí sử dụng tài liệu và công cụ học tập không?

Trả lời: Phần lớn tài liệu và công cụ học tập trên tic.edu.vn là miễn phí. Tuy nhiên, có thể có một số tài liệu hoặc dịch vụ nâng cao yêu cầu trả phí.

Câu hỏi 7: Tôi có thể tìm thấy thông tin về các khóa học và chương trình đào tạo trên tic.edu.vn không?

Trả lời: tic.edu.vn cung cấp thông tin về các khóa học, chương trình đào tạo, và cơ hội học bổng trong và ngoài nước, giúp bạn lựa chọn con đường học tập phù hợp với mục tiêu của mình.

Câu hỏi 8: Làm thế nào để liên hệ với đội ngũ hỗ trợ của tic.edu.vn nếu tôi có thắc mắc hoặc gặp vấn đề?

Trả lời: Bạn có thể liên hệ với chúng tôi qua email tic.edu@gmail.com hoặc sử dụng mẫu liên hệ trên trang web. Chúng tôi sẽ cố gắng phản hồi bạn trong thời gian sớm nhất.

Câu hỏi 9: tic.edu.vn có cập nhật thông tin giáo dục thường xuyên không?

Trả lời: Chúng tôi luôn nỗ lực cập nhật thông tin giáo dục mới nhất và chính xác nhất trên tic.edu.vn, bao gồm các thay đổi trong chương trình học, thông tin tuyển sinh, và các xu hướng giáo dục mới.

Câu hỏi 10: tic.edu.vn có phiên bản ứng dụng di động không?

Trả lời: Hiện tại, chúng tôi chưa có ứng dụng di động chính thức. Tuy nhiên, bạn có thể truy cập tic.edu.vn trên trình duyệt web của điện thoại hoặc máy tính bảng để trải nghiệm đầy đủ các tính năng.

Khám phá ngay tic.edu.vn để tiếp cận nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!