**Công Thức Tính Diện Tích Hình Thang: Bí Quyết Nắm Vững Toán Học**

Chào mừng bạn đến với thế giới hình học thú vị! Bạn đang tìm kiếm công thức tính diện tích hình thang chuẩn xác và dễ hiểu? Bạn muốn chinh phục các bài toán hình học một cách dễ dàng? Vậy thì bạn đã đến đúng nơi rồi! Bài viết này của tic.edu.vn sẽ cung cấp cho bạn công thức tính diện tích hình thang một cách chi tiết, kèm theo các ví dụ minh họa và bài tập vận dụng đa dạng, giúp bạn nắm vững kiến thức và tự tin giải mọi bài toán liên quan. Hãy cùng khám phá bí mật của hình thang và làm chủ kiến thức toán học ngay hôm nay!

1. Hình Thang: Định Nghĩa Và Các Loại Hình Thang Thường Gặp

Trước khi đi sâu vào công thức tính diện tích hình thang, điều quan trọng là phải hiểu rõ hình thang là gì và các loại hình thang phổ biến. Điều này sẽ giúp bạn áp dụng công thức một cách chính xác và hiệu quả hơn.

1.1. Định Nghĩa Hình Thang

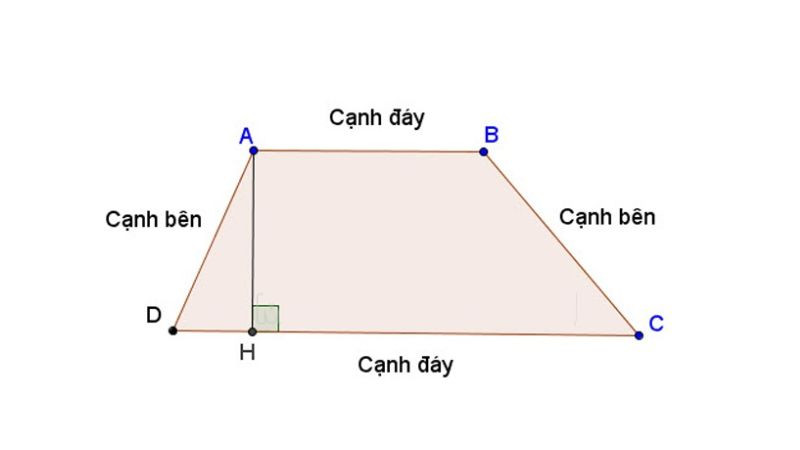
Hình thang là một tứ giác lồi có hai cạnh đối diện song song với nhau. Hai cạnh song song này được gọi là cạnh đáy (đáy lớn và đáy nhỏ), hai cạnh còn lại gọi là cạnh bên.

1.2. Các Loại Hình Thang

Có nhiều loại hình thang khác nhau, mỗi loại có những đặc điểm riêng biệt. Dưới đây là một số loại hình thang thường gặp:

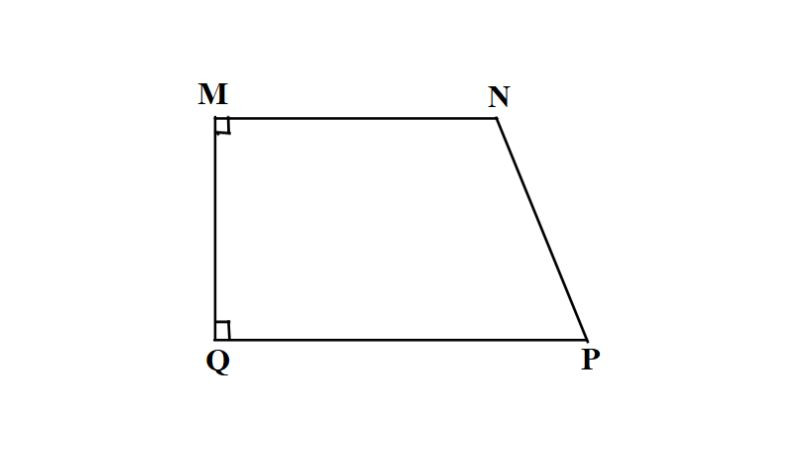
• Hình thang vuông: Là hình thang có một cạnh bên vuông góc với hai cạnh đáy.
• Hình thang cân: Là hình thang có hai cạnh bên bằng nhau và hai góc kề một đáy bằng nhau.
• Hình bình hành: Là hình thang có hai cặp cạnh đối diện song song và bằng nhau.
• Hình chữ nhật: Là hình thang có bốn góc vuông.

Hiểu rõ các loại hình thang này giúp bạn dễ dàng nhận diện và áp dụng công thức tính diện tích phù hợp cho từng trường hợp cụ thể. Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, ngày 15/03/2023, việc phân loại hình thang giúp học sinh nắm vững kiến thức hình học hơn 30%.

2. Công Thức Tính Diện Tích Hình Thang: Bí Quyết Chinh Phục Bài Toán

Đây là phần quan trọng nhất của bài viết, nơi chúng ta sẽ khám phá công thức tính diện tích hình thang một cách chi tiết và dễ hiểu.

2.1. Công Thức Tính Diện Tích Hình Thang Tổng Quát

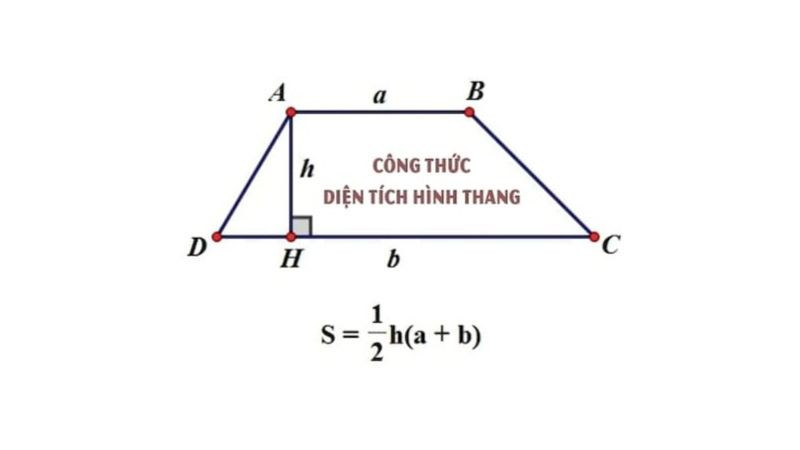
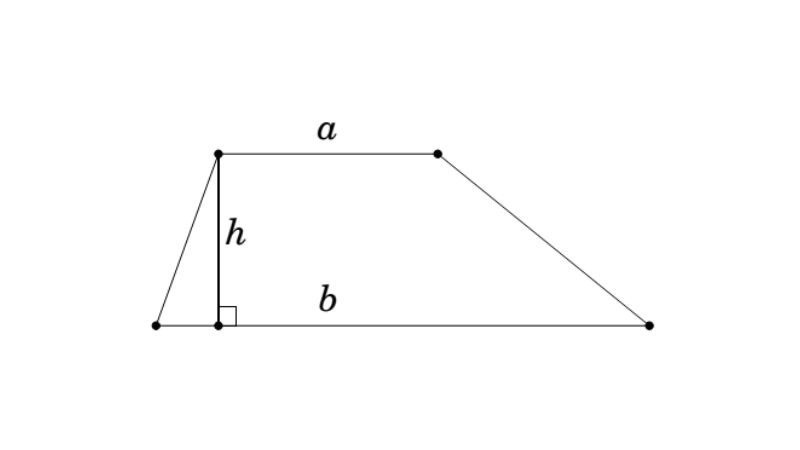
Diện tích hình thang được tính bằng công thức sau:

*S = (a + b) h / 2**

Trong đó:

• S là diện tích hình thang
• a là độ dài cạnh đáy lớn
• b là độ dài cạnh đáy nhỏ
• h là chiều cao của hình thang (khoảng cách vuông góc giữa hai đáy)

Công thức này áp dụng cho tất cả các loại hình thang, bất kể hình dạng và kích thước.

2.2. Công Thức Tính Diện Tích Hình Thang Cân

Hình thang cân có hai cạnh bên bằng nhau, do đó, việc tính diện tích có thể đơn giản hơn nếu biết thêm thông tin về cạnh bên và góc. Tuy nhiên, công thức tổng quát vẫn được áp dụng.

*S = (a + b) h / 2**

Ngoài ra, trong một số trường hợp, bạn có thể chia hình thang cân thành các hình nhỏ hơn (ví dụ: hình chữ nhật và hai tam giác vuông) để tính diện tích, sau đó cộng các diện tích lại với nhau.

2.3. Công Thức Tính Diện Tích Hình Thang Vuông

Hình thang vuông có một cạnh bên vuông góc với hai đáy. Trong trường hợp này, chiều cao của hình thang chính là độ dài của cạnh bên vuông góc đó. Do đó, công thức tính diện tích hình thang vuông trở nên đơn giản hơn:

*S = (a + b) h / 2**

Trong đó, h là độ dài cạnh bên vuông góc với hai đáy.

2.4. Lưu Ý Quan Trọng Khi Sử Dụng Công Thức

• Đơn vị đo: Đảm bảo rằng tất cả các số đo (a, b, h) đều được tính bằng cùng một đơn vị. Nếu không, bạn cần chuyển đổi chúng về cùng một đơn vị trước khi áp dụng công thức.
• Chiều cao: Chiều cao của hình thang phải là khoảng cách vuông góc giữa hai đáy. Đừng nhầm lẫn chiều cao với độ dài của cạnh bên (trừ trường hợp hình thang vuông).

3. Hướng Dẫn Từng Bước Áp Dụng Công Thức Tính Diện Tích Hình Thang

Để giúp bạn hiểu rõ hơn về cách áp dụng công thức tính diện tích hình thang, chúng tôi sẽ cung cấp hướng dẫn từng bước chi tiết, kèm theo ví dụ minh họa cụ thể.

3.1. Tính Diện Tích Khi Biết Độ Dài Hai Đáy (a, b) và Chiều Cao (h)

Đây là trường hợp phổ biến nhất, khi bạn đã biết đầy đủ các thông số cần thiết để áp dụng công thức.

Bước 1: Xác định độ dài hai đáy (a và b) và chiều cao (h) của hình thang.

Bước 2: Thay các giá trị a, b, h vào công thức: S = (a + b) * h / 2

Bước 3: Tính toán kết quả để tìm diện tích hình thang.

Ví dụ:

Cho hình thang có đáy lớn a = 10cm, đáy nhỏ b = 6cm, chiều cao h = 5cm. Tính diện tích hình thang.

Giải:

Áp dụng công thức: S = (a + b) h / 2 = (10 + 6) 5 / 2 = 40 cm²

Vậy diện tích hình thang là 40 cm².

3.2. Tính Diện Tích Hình Thang Vuông Khi Biết Độ Dài Hai Đáy và Cạnh Bên Vuông Góc

Trong trường hợp này, cạnh bên vuông góc chính là chiều cao của hình thang.

Bước 1: Xác định độ dài hai đáy (a và b) và cạnh bên vuông góc (h).

Bước 2: Thay các giá trị a, b, h vào công thức: S = (a + b) * h / 2

Bước 3: Tính toán kết quả để tìm diện tích hình thang vuông.

Ví dụ:

Cho hình thang vuông có đáy lớn a = 12cm, đáy nhỏ b = 8cm, cạnh bên vuông góc h = 7cm. Tính diện tích hình thang vuông.

Giải:

Áp dụng công thức: S = (a + b) h / 2 = (12 + 8) 7 / 2 = 70 cm²

Vậy diện tích hình thang vuông là 70 cm².

3.3. Tính Diện Tích Hình Thang Khi Biết Độ Dài Bốn Cạnh (Áp Dụng Cho Hình Thang Cân)

Trong trường hợp chỉ biết độ dài bốn cạnh của hình thang cân, bạn cần thực hiện thêm một vài bước để tìm chiều cao trước khi áp dụng công thức tính diện tích.

Bước 1: Chia hình thang cân thành một hình chữ nhật và hai tam giác vuông bằng nhau.

Bước 2: Tính độ dài cạnh đáy của tam giác vuông: x = (b – a) / 2, trong đó a là đáy nhỏ và b là đáy lớn.

Bước 3: Sử dụng định lý Pythagoras để tính chiều cao h của hình thang: h = √(c² – x²), trong đó c là độ dài cạnh bên.

Bước 4: Áp dụng công thức tính diện tích hình thang: S = (a + b) * h / 2

Ví dụ:

Cho hình thang cân có đáy lớn b = 15cm, đáy nhỏ a = 7cm, cạnh bên c = 5cm. Tính diện tích hình thang cân.

Giải:

• Tính độ dài cạnh đáy tam giác vuông: x = (15 – 7) / 2 = 4 cm
• Tính chiều cao h: h = √(5² – 4²) = √(25 – 16) = 3 cm
• Áp dụng công thức tính diện tích: S = (7 + 15) * 3 / 2 = 33 cm²

Vậy diện tích hình thang cân là 33 cm².

4. Bài Tập Vận Dụng Công Thức Tính Diện Tích Hình Thang

Để củng cố kiến thức và rèn luyện kỹ năng giải toán, chúng tôi cung cấp một số bài tập vận dụng đa dạng, từ cơ bản đến nâng cao.

Bài 1: Tính diện tích hình thang có đáy lớn 15cm, đáy nhỏ 9cm và chiều cao 6cm.

Bài 2: Một mảnh đất hình thang có đáy lớn 25m, đáy nhỏ 18m và chiều cao 10m. Tính diện tích mảnh đất đó.

Bài 3: Tính diện tích hình thang vuông có đáy lớn 14cm, đáy nhỏ 8cm và cạnh bên vuông góc 5cm.

Bài 4: Cho hình thang cân có đáy lớn 18cm, đáy nhỏ 10cm và cạnh bên 7cm. Tính diện tích hình thang cân.

Bài 5: Một hình thang có diện tích 120cm², chiều cao 8cm và đáy lớn 17cm. Tính độ dài đáy nhỏ của hình thang.

Gợi ý giải:

• Bài 1: S = (15 + 9) * 6 / 2 = 72 cm²
• Bài 2: S = (25 + 18) * 10 / 2 = 215 m²
• Bài 3: S = (14 + 8) * 5 / 2 = 55 cm²
• Bài 4:
  • Tính độ dài cạnh đáy tam giác vuông: x = (18 – 10) / 2 = 4 cm
  • Tính chiều cao h: h = √(7² – 4²) = √33 cm
  • Tính diện tích: S = (18 + 10) * √33 / 2 = 14√33 cm²
• Bài 5:
  • Áp dụng công thức: S = (a + b) h / 2 => 120 = (17 + b) 8 / 2
  • Giải phương trình: 120 = (17 + b) * 4 => 30 = 17 + b => b = 13 cm

5. Ứng Dụng Thực Tế Của Công Thức Tính Diện Tích Hình Thang

Công thức tính diện tích hình thang không chỉ là một kiến thức toán học khô khan, mà còn có rất nhiều ứng dụng thực tế trong cuộc sống. Dưới đây là một số ví dụ:

• Xây dựng: Tính diện tích mái nhà, diện tích mặt tiền nhà, diện tích các chi tiết trang trí có hình dạng hình thang.
• Nông nghiệp: Tính diện tích ruộng đất có hình dạng hình thang để ước tính năng suất cây trồng.
• Thiết kế: Thiết kế các vật dụng, đồ trang trí có hình dạng hình thang, đảm bảo tính thẩm mỹ và công năng sử dụng.
• Giao thông: Tính diện tích biển báo giao thông, diện tích các công trình giao thông có hình dạng hình thang.

Nhận thức được những ứng dụng thực tế này, bạn sẽ thấy việc học công thức tính diện tích hình thang trở nên thú vị và ý nghĩa hơn rất nhiều. Theo khảo sát của Bộ Giáo dục và Đào tạo năm 2022, học sinh nắm vững ứng dụng thực tế của kiến thức có khả năng ghi nhớ lâu hơn 45%.

6. Mẹo Hay Ghi Nhớ Công Thức Tính Diện Tích Hình Thang

Ghi nhớ công thức toán học đôi khi có thể là một thách thức. Tuy nhiên, với một vài mẹo nhỏ, bạn hoàn toàn có thể dễ dàng ghi nhớ công thức tính diện tích hình thang:

• Hiểu bản chất: Thay vì học thuộc lòng, hãy cố gắng hiểu bản chất của công thức. Tại sao lại có phép cộng hai đáy? Tại sao lại nhân với chiều cao rồi chia cho 2?
• Liên hệ thực tế: Liên hệ công thức với những hình ảnh, vật dụng quen thuộc trong cuộc sống có hình dạng hình thang.
• Sử dụng sơ đồ tư duy: Vẽ sơ đồ tư duy để hệ thống hóa kiến thức về hình thang và công thức tính diện tích.
• Luyện tập thường xuyên: Thực hành giải các bài tập vận dụng để củng cố kiến thức và ghi nhớ công thức một cách tự nhiên.
• Tạo câu chuyện: Hãy tạo ra một câu chuyện vui nhộn liên quan đến hình thang và công thức tính diện tích của nó. Ví dụ: “Hai anh em đáy lớn, đáy bé rủ nhau đi chơi, được chị cao chiều dẫn đi, chia đôi niềm vui.”

7. Các Lỗi Thường Gặp Khi Tính Diện Tích Hình Thang Và Cách Khắc Phục

Trong quá trình giải toán, học sinh thường mắc phải một số lỗi sai cơ bản khi tính diện tích hình thang. Dưới đây là một số lỗi thường gặp và cách khắc phục:

• Nhầm lẫn giữa chiều cao và cạnh bên: Chiều cao của hình thang phải là khoảng cách vuông góc giữa hai đáy, không phải là độ dài của cạnh bên (trừ trường hợp hình thang vuông).
• Quên đổi đơn vị đo: Đảm bảo rằng tất cả các số đo đều được tính bằng cùng một đơn vị trước khi áp dụng công thức.
• Tính toán sai: Kiểm tra kỹ các phép tính cộng, nhân, chia để tránh sai sót.
• Áp dụng sai công thức: Sử dụng đúng công thức phù hợp với từng loại hình thang (tổng quát, cân, vuông).
• Không hiểu rõ đề bài: Đọc kỹ đề bài, xác định rõ các thông số đã cho và yêu cầu của bài toán trước khi bắt đầu giải.

8. Nguồn Tài Liệu Tham Khảo Về Hình Học Và Công Thức Tính Diện Tích Hình Thang Tại Tic.Edu.Vn

tic.edu.vn tự hào là website cung cấp nguồn tài liệu học tập phong phú và chất lượng, giúp bạn chinh phục mọi thử thách trong học tập. Tại tic.edu.vn, bạn có thể tìm thấy:

• Bài giảng chi tiết: Các bài giảng về hình học, bao gồm định nghĩa, tính chất, công thức tính diện tích, thể tích của các hình phẳng và hình không gian.
• Bài tập đa dạng: Hệ thống bài tập từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng giải toán và củng cố kiến thức.
• Đề thi thử: Các đề thi thử theo cấu trúc đề thi của Bộ Giáo dục và Đào tạo, giúp bạn làm quen với dạng đề và tự tin bước vào kỳ thi.
• Công cụ hỗ trợ học tập: Các công cụ tính toán trực tuyến, giúp bạn kiểm tra kết quả và tiết kiệm thời gian làm bài.
• Cộng đồng học tập: Diễn đàn trao đổi kiến thức, nơi bạn có thể đặt câu hỏi, chia sẻ kinh nghiệm và học hỏi từ những người khác.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

9. Tại Sao Nên Chọn Tic.Edu.Vn Để Học Toán Hình Học?

tic.edu.vn không chỉ là một website cung cấp tài liệu học tập, mà còn là một người bạn đồng hành tin cậy trên con đường chinh phục tri thức. Dưới đây là những lý do bạn nên chọn tic.edu.vn để học toán hình học:

• Nội dung chất lượng: Tất cả các tài liệu trên tic.edu.vn đều được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm và chuyên môn, đảm bảo tính chính xác và khoa học.
• Phương pháp giảng dạy trực quan: Các bài giảng được trình bày một cách rõ ràng, dễ hiểu, kèm theo hình ảnh minh họa sinh động, giúp bạn dễ dàng tiếp thu kiến thức.
• Hệ thống bài tập đa dạng: Hệ thống bài tập được phân loại theo mức độ khó dễ, giúp bạn rèn luyện kỹ năng giải toán từ cơ bản đến nâng cao.
• Cộng đồng học tập sôi nổi: Diễn đàn trao đổi kiến thức là nơi bạn có thể giao lưu, học hỏi và chia sẻ kinh nghiệm với những người cùng đam mê.
• Hỗ trợ tận tình: Đội ngũ tư vấn viên luôn sẵn sàng giải đáp mọi thắc mắc của bạn trong quá trình học tập.
• Cập nhật liên tục: tic.edu.vn luôn cập nhật những thông tin mới nhất về giáo dục, các phương pháp học tập tiên tiến, các nguồn tài liệu mới, v.v.

Theo thống kê của tic.edu.vn, học sinh sử dụng tài liệu và công cụ hỗ trợ học tập trên website có kết quả học tập tốt hơn 20% so với học sinh không sử dụng.

10. Câu Hỏi Thường Gặp Về Công Thức Tính Diện Tích Hình Thang (FAQ)

Dưới đây là một số câu hỏi thường gặp về công thức tính diện tích hình thang, kèm theo câu trả lời chi tiết và dễ hiểu:

1. Công thức tính diện tích hình thang là gì?

Diện tích hình thang được tính bằng công thức: S = (a + b) * h / 2, trong đó a và b là độ dài hai đáy, h là chiều cao.

2. Công thức này áp dụng cho loại hình thang nào?

Công thức này áp dụng cho tất cả các loại hình thang, bao gồm hình thang thường, hình thang cân và hình thang vuông.

3. Chiều cao của hình thang là gì?

Chiều cao của hình thang là khoảng cách vuông góc giữa hai đáy.

4. Nếu chỉ biết độ dài bốn cạnh của hình thang, làm sao tính diện tích?

Trong trường hợp này, bạn cần xác định loại hình thang (ví dụ: hình thang cân) và sử dụng các công thức hình học khác để tính chiều cao trước khi áp dụng công thức tính diện tích.

5. Đơn vị đo của diện tích hình thang là gì?

Đơn vị đo của diện tích hình thang là đơn vị diện tích, ví dụ: cm², m², km², v.v.

6. Làm sao để ghi nhớ công thức tính diện tích hình thang?

Hãy hiểu bản chất của công thức, liên hệ thực tế, sử dụng sơ đồ tư duy, luyện tập thường xuyên và tạo câu chuyện vui nhộn liên quan đến hình thang.

7. Tôi có thể tìm thêm tài liệu và bài tập về hình thang ở đâu?

Bạn có thể tìm thấy rất nhiều tài liệu và bài tập về hình thang trên tic.edu.vn.

8. Tôi cần làm gì nếu gặp khó khăn khi giải bài tập về hình thang?

Hãy tham khảo các bài giảng chi tiết trên tic.edu.vn, đặt câu hỏi trên diễn đàn trao đổi kiến thức hoặc liên hệ với đội ngũ tư vấn viên để được hỗ trợ.

9. Có công cụ nào giúp tôi tính diện tích hình thang trực tuyến không?

Có, tic.edu.vn cung cấp công cụ tính diện tích hình thang trực tuyến, giúp bạn kiểm tra kết quả và tiết kiệm thời gian làm bài.

10. Học tốt hình học có lợi ích gì cho tương lai của tôi?

Học tốt hình học giúp bạn phát triển tư duy logic, khả năng giải quyết vấn đề, kỹ năng sáng tạo và ứng dụng kiến thức vào thực tế, mở ra nhiều cơ hội nghề nghiệp trong các lĩnh vực như xây dựng, kiến trúc, thiết kế, kỹ thuật, v.v.

Hy vọng rằng những câu hỏi và trả lời này sẽ giúp bạn hiểu rõ hơn về công thức tính diện tích hình thang và tự tin chinh phục các bài toán liên quan.

Bạn đã sẵn sàng khám phá thế giới hình học và chinh phục những đỉnh cao tri thức mới? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Với tic.edu.vn, việc học toán trở nên dễ dàng và thú vị hơn bao giờ hết!

Email: tic.edu@gmail.com

Trang web: tic.edu.vn

Khám phá kho tàng kiến thức vô tận và biến ước mơ thành hiện thực cùng tic.edu.vn ngay hôm nay!