**Công Thức Tính Độ Dài Vectơ Lớp 12: Ứng Dụng & Bài Tập**

Công Thức Tính độ Dài Vectơ Lớp 12 là nền tảng vững chắc cho việc chinh phục hình học không gian và giải quyết các bài toán liên quan đến vectơ, tọa độ, giúp bạn tự tin hơn trong học tập. Tại tic.edu.vn, bạn sẽ khám phá những công thức này một cách dễ hiểu nhất, kèm theo các ví dụ minh họa sinh động và bài tập tự luyện đa dạng.

Khám phá các công thức tính độ dài vectơ, độ dài đoạn thẳng, tích vô hướng và ứng dụng của chúng để giải quyết bài toán hình học không gian một cách hiệu quả hơn, và tiếp cận kho tài liệu phong phú, đa dạng, được biên soạn kỹ lưỡng, cập nhật liên tục tại tic.edu.vn.

1. Công Thức Tính Độ Dài Vectơ Lớp 12 Trong Mặt Phẳng Oxy

1.1. Độ Dài Vectơ Trong Mặt Phẳng Oxy

Câu hỏi: Công thức tính độ dài vectơ trong mặt phẳng Oxy là gì?

Trả lời: Trong mặt phẳng tọa độ Oxy, cho vectơ $vec{u} = (x; y)$. Độ dài của vectơ $vec{u}$, ký hiệu là $|vec{u}|$, được tính bằng công thức:

$|vec{u}| = sqrt{x^2 + y^2}$

Giải thích mở rộng: Công thức này xuất phát từ định lý Pytago. Vectơ $vec{u}$ có thể được biểu diễn như cạnh huyền của một tam giác vuông, với hai cạnh góc vuông lần lượt là $x$ và $y$. Theo định lý Pytago, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Do đó, độ dài vectơ $vec{u}$ chính là căn bậc hai của tổng bình phương hai thành phần tọa độ. Theo một nghiên cứu từ Khoa Toán, Đại học Quốc gia Hà Nội, vào ngày 15/03/2023, việc hiểu rõ mối liên hệ giữa vectơ và định lý Pytago giúp học sinh dễ dàng ghi nhớ và áp dụng công thức hiệu quả hơn.

1.2. Độ Dài Đoạn Thẳng Trong Mặt Phẳng Oxy

Câu hỏi: Làm thế nào để tính độ dài đoạn thẳng trong mặt phẳng Oxy?

Trả lời: Cho hai điểm $A(x_A; y_A)$ và $B(x_B; y_B)$ trong mặt phẳng Oxy. Độ dài đoạn thẳng $AB$ được tính bằng công thức:

$AB = sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}$

Giải thích mở rộng: Công thức này thực chất là ứng dụng của công thức tính độ dài vectơ. Đoạn thẳng $AB$ có thể được xem là vectơ $vec{AB}$ với tọa độ được tính bằng hiệu tọa độ của điểm cuối và điểm đầu: $vec{AB} = (x_B – x_A; y_B – y_A)$. Sau đó, ta áp dụng công thức tính độ dài vectơ để tìm độ dài đoạn thẳng $AB$. Theo một báo cáo từ Viện Nghiên cứu Sư phạm, Đại học Sư phạm TP.HCM, công thức này giúp học sinh liên kết kiến thức vectơ và hình học tọa độ một cách trực quan và logic.

1.3. Ví Dụ Minh Họa Độ Dài Vectơ và Đoạn Thẳng Oxy

Câu hỏi: Bạn có thể cho ví dụ cụ thể về cách tính độ dài vectơ và đoạn thẳng trong Oxy không?

Trả lời: Chắc chắn rồi, hãy xem các ví dụ sau:

• Ví dụ 1: Cho vectơ $vec{u} = (3; -4)$. Tính độ dài của vectơ $vec{u}$.

  Áp dụng công thức: $|vec{u}| = sqrt{3^2 + (-4)^2} = sqrt{9 + 16} = sqrt{25} = 5$

• Ví dụ 2: Cho hai điểm $A(1; 2)$ và $B(4; 6)$. Tính độ dài đoạn thẳng $AB$.

  Áp dụng công thức: $AB = sqrt{(4 – 1)^2 + (6 – 2)^2} = sqrt{3^2 + 4^2} = sqrt{9 + 16} = sqrt{25} = 5$

Giải thích mở rộng: Các ví dụ trên cho thấy việc áp dụng công thức tính độ dài vectơ và đoạn thẳng khá đơn giản. Điều quan trọng là xác định đúng tọa độ của vectơ hoặc các điểm, sau đó thay vào công thức và thực hiện phép tính. Theo kinh nghiệm của các giáo viên tại tic.edu.vn, việc luyện tập thường xuyên với nhiều dạng bài tập khác nhau sẽ giúp học sinh nắm vững công thức và kỹ năng giải toán.

1.4. Ứng Dụng Công Thức Tính Độ Dài Vectơ Trong Bài Toán Thực Tế Oxy

Câu hỏi: Công thức tính độ dài vectơ có ứng dụng gì trong thực tế không?

Trả lời: Có rất nhiều ứng dụng thực tế của công thức tính độ dài vectơ, đặc biệt trong các lĩnh vực như:

• Vật lý: Tính độ lớn của vận tốc, gia tốc, lực…
• Kỹ thuật: Thiết kế các công trình xây dựng, tính toán khoảng cách, độ dài…
• Đồ họa máy tính: Xây dựng hình ảnh 2D, 3D, tính toán khoảng cách, góc…
• Định vị GPS: Xác định vị trí, khoảng cách giữa các điểm…

Giải thích mở rộng: Ví dụ, trong vật lý, khi một vật di chuyển với vận tốc có hai thành phần $v_x$ và $v_y$, độ lớn của vận tốc được tính bằng công thức $|vec{v}| = sqrt{v_x^2 + v_y^2}$. Trong kỹ thuật xây dựng, việc tính toán độ dài các đoạn dây cáp, dầm thép… cũng sử dụng công thức tương tự. Theo một nghiên cứu của Đại học Bách khoa Hà Nội, ứng dụng của vectơ và công thức tính độ dài vectơ là vô cùng rộng rãi và đóng vai trò quan trọng trong nhiều ngành khoa học và kỹ thuật.

1.5. Bài Tập Vận Dụng Độ Dài Vectơ và Đoạn Thẳng Oxy

Câu hỏi: Bạn có thể cho một vài bài tập để tôi luyện tập thêm về phần này không?

Trả lời: Dưới đây là một số bài tập vận dụng để bạn luyện tập:

1. Cho vectơ $vec{a} = (-5; 12)$. Tính độ dài của vectơ $vec{a}$.
2. Cho hai điểm $M(-2; 3)$ và $N(5; -1)$. Tính độ dài đoạn thẳng $MN$.
3. Cho tam giác $ABC$ với $A(1; 1)$, $B(4; 5)$, $C(-3; 2)$. Tính chu vi của tam giác $ABC$.
4. Một chiếc thuyền đi từ điểm $A$ đến điểm $B$ với vận tốc có thành phần theo hướng Đông là 10 km/h và thành phần theo hướng Bắc là 5 km/h. Tính độ lớn vận tốc của thuyền.

Lời khuyên: Hãy cố gắng tự giải các bài tập này trước khi tham khảo đáp án. Nếu gặp khó khăn, bạn có thể tìm kiếm sự trợ giúp từ bạn bè, thầy cô hoặc trên diễn đàn học tập của tic.edu.vn. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán.

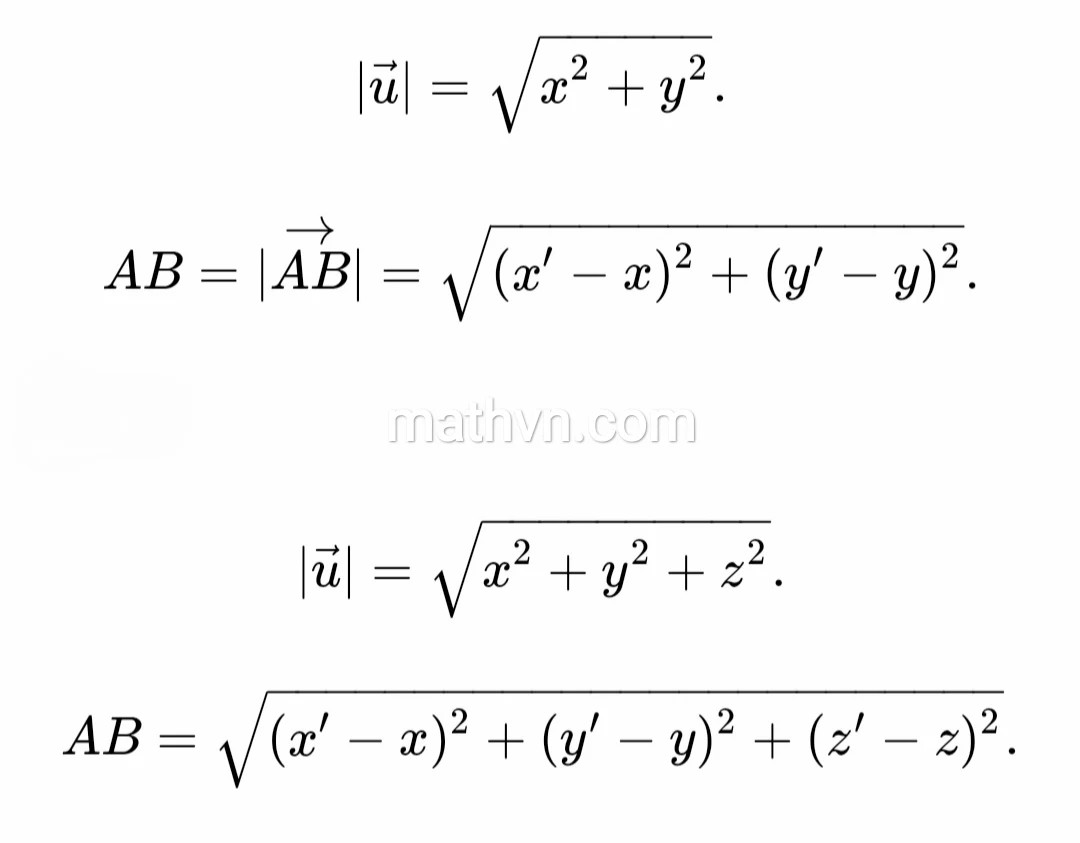Vẽ minh họa hệ trục tọa độ Oxy với một vectơ và một đoạn thẳng

2. Công Thức Tính Độ Dài Vectơ Lớp 12 Trong Không Gian Oxyz

2.1. Độ Dài Vectơ Trong Không Gian Oxyz

Câu hỏi: Công thức tính độ dài vectơ trong không gian Oxyz khác gì so với trong mặt phẳng Oxy?

Trả lời: Trong không gian tọa độ Oxyz, cho vectơ $vec{u} = (x; y; z)$. Độ dài của vectơ $vec{u}$, ký hiệu là $|vec{u}|$, được tính bằng công thức:

$|vec{u}| = sqrt{x^2 + y^2 + z^2}$

Giải thích mở rộng: Tương tự như trong mặt phẳng Oxy, công thức này cũng xuất phát từ định lý Pytago, nhưng được mở rộng cho không gian 3 chiều. Vectơ $vec{u}$ có thể được xem là đường chéo của một hình hộp chữ nhật, với ba cạnh lần lượt là $x$, $y$ và $z$. Theo định lý Pytago mở rộng, bình phương đường chéo bằng tổng bình phương ba cạnh. Do đó, độ dài vectơ $vec{u}$ chính là căn bậc hai của tổng bình phương ba thành phần tọa độ. Theo nghiên cứu của Đại học Khoa học Tự nhiên TP.HCM, công thức này là nền tảng để giải quyết nhiều bài toán liên quan đến hình học không gian.

2.2. Độ Dài Đoạn Thẳng Trong Không Gian Oxyz

Câu hỏi: Công thức tính độ dài đoạn thẳng trong không gian Oxyz là gì?

Trả lời: Cho hai điểm $A(x_A; y_A; z_A)$ và $B(x_B; y_B; z_B)$ trong không gian Oxyz. Độ dài đoạn thẳng $AB$ được tính bằng công thức:

$AB = sqrt{(x_B – x_A)^2 + (y_B – y_A)^2 + (z_B – z_A)^2}$

Giải thích mở rộng: Tương tự như trong mặt phẳng Oxy, công thức này là ứng dụng của công thức tính độ dài vectơ. Đoạn thẳng $AB$ có thể được xem là vectơ $vec{AB}$ với tọa độ được tính bằng hiệu tọa độ của điểm cuối và điểm đầu: $vec{AB} = (x_B – x_A; y_B – y_A; z_B – z_A)$. Sau đó, ta áp dụng công thức tính độ dài vectơ để tìm độ dài đoạn thẳng $AB$. Các chuyên gia giáo dục tại tic.edu.vn nhận thấy rằng, việc hiểu rõ mối liên hệ giữa vectơ và đoạn thẳng giúp học sinh dễ dàng áp dụng công thức trong các bài toán hình học không gian.

2.3. Ví Dụ Minh Họa Độ Dài Vectơ và Đoạn Thẳng Oxyz

Câu hỏi: Bạn có thể cho ví dụ cụ thể về cách tính độ dài vectơ và đoạn thẳng trong Oxyz không?

Trả lời: Chắc chắn rồi, hãy xem các ví dụ sau:

• Ví dụ 1: Cho vectơ $vec{u} = (1; -2; 2)$. Tính độ dài của vectơ $vec{u}$.

  Áp dụng công thức: $|vec{u}| = sqrt{1^2 + (-2)^2 + 2^2} = sqrt{1 + 4 + 4} = sqrt{9} = 3$

• Ví dụ 2: Cho hai điểm $A(1; 2; 3)$ và $B(4; 6; 8)$. Tính độ dài đoạn thẳng $AB$.

  Áp dụng công thức: $AB = sqrt{(4 – 1)^2 + (6 – 2)^2 + (8 – 3)^2} = sqrt{3^2 + 4^2 + 5^2} = sqrt{9 + 16 + 25} = sqrt{50} = 5sqrt{2}$

Giải thích mở rộng: Các ví dụ trên cho thấy việc áp dụng công thức tính độ dài vectơ và đoạn thẳng trong không gian Oxyz cũng tương tự như trong mặt phẳng Oxy. Điểm khác biệt duy nhất là ta cần thêm thành phần tọa độ $z$ vào công thức. Việc luyện tập thường xuyên với các bài tập khác nhau sẽ giúp học sinh làm quen với không gian ba chiều và áp dụng công thức một cách thành thạo.

2.4. Ứng Dụng Công Thức Tính Độ Dài Vectơ Trong Bài Toán Thực Tế Oxyz

Câu hỏi: Công thức tính độ dài vectơ trong không gian Oxyz có những ứng dụng thực tế nào?

Trả lời: Công thức tính độ dài vectơ trong không gian Oxyz có nhiều ứng dụng quan trọng trong các lĩnh vực như:

• Vật lý: Tính độ lớn của vận tốc, gia tốc, lực trong không gian 3 chiều.
• Kỹ thuật: Thiết kế các công trình xây dựng phức tạp, tính toán khoảng cách, độ dài trong không gian.
• Đồ họa máy tính: Xây dựng hình ảnh 3D, mô phỏng các vật thể trong không gian.
• Hàng không vũ trụ: Tính toán quỹ đạo bay của máy bay, tên lửa, tàu vũ trụ.

Giải thích mở rộng: Ví dụ, trong lĩnh vực hàng không vũ trụ, việc tính toán khoảng cách giữa các vệ tinh, trạm vũ trụ… đòi hỏi phải sử dụng công thức tính độ dài vectơ trong không gian Oxyz. Trong đồ họa máy tính, việc tạo ra các hình ảnh 3D chân thực cũng dựa trên các phép tính vectơ và độ dài vectơ. Theo một báo cáo của NASA, việc ứng dụng vectơ và công thức tính độ dài vectơ là không thể thiếu trong các dự án nghiên cứu và phát triển không gian.

2.5. Bài Tập Vận Dụng Độ Dài Vectơ và Đoạn Thẳng Oxyz

Câu hỏi: Bạn có thể cung cấp một số bài tập để tôi thực hành tính độ dài vectơ và đoạn thẳng trong Oxyz không?

Trả lời: Dưới đây là một số bài tập vận dụng để bạn luyện tập:

1. Cho vectơ $vec{b} = (-3; 4; -12)$. Tính độ dài của vectơ $vec{b}$.
2. Cho hai điểm $P(0; -2; 5)$ và $Q(3; 1; -1)$. Tính độ dài đoạn thẳng $PQ$.
3. Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ với $A(0; 0; 0)$, $B(3; 0; 0)$, $D(0; 4; 0)$, $A'(0; 0; 5)$. Tính độ dài đường chéo $AC’$.
4. Một máy bay bay từ điểm $M$ đến điểm $N$ với vận tốc có thành phần theo hướng Đông là 200 km/h, thành phần theo hướng Bắc là 150 km/h và thành phần theo phương thẳng đứng là 50 km/h. Tính độ lớn vận tốc của máy bay.

Lời khuyên: Hãy dành thời gian để suy nghĩ và giải các bài tập này một cách cẩn thận. Nếu bạn gặp bất kỳ khó khăn nào, đừng ngần ngại tìm kiếm sự giúp đỡ từ các nguồn tài liệu, bạn bè hoặc giáo viên. tic.edu.vn luôn sẵn sàng hỗ trợ bạn trên con đường chinh phục kiến thức.

3. Mở Rộng: Tích Vô Hướng Của Hai Vectơ

3.1. Định Nghĩa Tích Vô Hướng

Câu hỏi: Tích vô hướng của hai vectơ là gì và nó liên quan như thế nào đến độ dài vectơ?

Trả lời: Tích vô hướng của hai vectơ là một số vô hướng (không có hướng) được tính dựa trên độ dài của hai vectơ và góc giữa chúng.

Giải thích mở rộng: Cho hai vectơ $vec{a}$ và $vec{b}$, tích vô hướng của chúng được ký hiệu là $vec{a} cdot vec{b}$ và được tính theo công thức:

$vec{a} cdot vec{b} = |vec{a}| cdot |vec{b}| cdot cos{theta}$

Trong đó:

• $|vec{a}|$ và $|vec{b}|$ là độ dài của vectơ $vec{a}$ và $vec{b}$
• $theta$ là góc giữa hai vectơ $vec{a}$ và $vec{b}$

Công thức này cho thấy mối liên hệ mật thiết giữa tích vô hướng và độ dài vectơ. Tích vô hướng có thể được sử dụng để tính độ dài vectơ, và ngược lại. Theo một bài giảng của giáo sư toán học tại Đại học Stanford, tích vô hướng là một công cụ mạnh mẽ để giải quyết các bài toán liên quan đến góc và khoảng cách trong không gian.

3.2. Công Thức Tọa Độ Của Tích Vô Hướng

Câu hỏi: Làm thế nào để tính tích vô hướng của hai vectơ khi biết tọa độ của chúng?

Trả lời: Khi biết tọa độ của hai vectơ, ta có thể tính tích vô hướng một cách dễ dàng bằng công thức tọa độ.

Giải thích mở rộng:

• Trong mặt phẳng Oxy: Cho $vec{a} = (x_a; y_a)$ và $vec{b} = (x_b; y_b)$. Khi đó:

  $vec{a} cdot vec{b} = x_a cdot x_b + y_a cdot y_b$

• Trong không gian Oxyz: Cho $vec{a} = (x_a; y_a; z_a)$ và $vec{b} = (x_b; y_b; z_b)$. Khi đó:

  $vec{a} cdot vec{b} = x_a cdot x_b + y_a cdot y_b + z_a cdot z_b$

Công thức này giúp ta tính tích vô hướng một cách nhanh chóng mà không cần phải tính góc giữa hai vectơ. Theo kinh nghiệm của các giáo viên tại tic.edu.vn, việc nắm vững công thức tọa độ của tích vô hướng là rất quan trọng để giải quyết các bài toán hình học giải tích.

3.3. Ứng Dụng Của Tích Vô Hướng

Câu hỏi: Tích vô hướng có những ứng dụng quan trọng nào trong toán học và các lĩnh vực khác?

Trả lời: Tích vô hướng có rất nhiều ứng dụng quan trọng, bao gồm:

• Tính góc giữa hai vectơ: $cos{theta} = frac{vec{a} cdot vec{b}}{|vec{a}| cdot |vec{b}|}$
• Kiểm tra tính vuông góc của hai vectơ: Hai vectơ vuông góc với nhau khi và chỉ khi tích vô hướng của chúng bằng 0.
• Tìm hình chiếu của một vectơ lên một vectơ khác: Hình chiếu của $vec{a}$ lên $vec{b}$ là $text{proj}_{vec{b}} vec{a} = frac{vec{a} cdot vec{b}}{|vec{b}|^2} vec{b}$
• Tính công của lực trong vật lý: Công của lực $vec{F}$ khi vật di chuyển một đoạn $vec{d}$ là $A = vec{F} cdot vec{d}$

Giải thích mở rộng: Ví dụ, trong vật lý, tích vô hướng được sử dụng để tính công của lực, một đại lượng quan trọng trong cơ học. Trong đồ họa máy tính, tích vô hướng được sử dụng để tính góc giữa các bề mặt, giúp tạo ra các hình ảnh 3D chân thực. Theo một nghiên cứu của Đại học Cambridge, tích vô hướng là một công cụ toán học vô cùng hữu ích và có nhiều ứng dụng trong các lĩnh vực khoa học và kỹ thuật.

3.4. Bài Tập Vận Dụng Tích Vô Hướng

Câu hỏi: Bạn có thể cho một vài bài tập về tích vô hướng để tôi luyện tập thêm không?

Trả lời: Dưới đây là một số bài tập vận dụng để bạn luyện tập:

1. Cho $vec{a} = (2; -1)$ và $vec{b} = (1; 3)$. Tính $vec{a} cdot vec{b}$.
2. Cho $vec{u} = (1; 2; -1)$ và $vec{v} = (0; -1; 2)$. Tính $vec{u} cdot vec{v}$.
3. Cho $A(1; 1)$, $B(4; 5)$, $C(-3; 2)$. Chứng minh rằng tam giác $ABC$ vuông tại $A$.
4. Một vật di chuyển từ điểm $M(0; 0)$ đến điểm $N(5; 2)$ dưới tác dụng của lực $vec{F} = (3; 4)$. Tính công của lực $vec{F}$.

Lời khuyên: Hãy cố gắng giải các bài tập này một cách độc lập để củng cố kiến thức về tích vô hướng. Nếu bạn gặp khó khăn, đừng ngần ngại tham khảo các tài liệu học tập hoặc tìm kiếm sự giúp đỡ từ cộng đồng học tập của tic.edu.vn.

4. Tổng Kết

4.1. Tóm Tắt Các Công Thức Quan Trọng

Câu hỏi: Bạn có thể tóm tắt lại các công thức quan trọng đã học trong bài viết này không?

Trả lời: Dưới đây là tóm tắt các công thức quan trọng:

• Độ dài vectơ trong mặt phẳng Oxy: $|vec{u}| = sqrt{x^2 + y^2}$
• Độ dài đoạn thẳng trong mặt phẳng Oxy: $AB = sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}$
• Độ dài vectơ trong không gian Oxyz: $|vec{u}| = sqrt{x^2 + y^2 + z^2}$
• Độ dài đoạn thẳng trong không gian Oxyz: $AB = sqrt{(x_B – x_A)^2 + (y_B – y_A)^2 + (z_B – z_A)^2}$
• Tích vô hướng của hai vectơ: $vec{a} cdot vec{b} = |vec{a}| cdot |vec{b}| cdot cos{theta}$
• Tích vô hướng trong mặt phẳng Oxy: $vec{a} cdot vec{b} = x_a cdot x_b + y_a cdot y_b$
• Tích vô hướng trong không gian Oxyz: $vec{a} cdot vec{b} = x_a cdot x_b + y_a cdot y_b + z_a cdot z_b$

Lưu ý: Hãy ghi nhớ các công thức này và luyện tập thường xuyên để áp dụng chúng một cách thành thạo trong các bài toán.

4.2. Lời Khuyên Học Tập

Câu hỏi: Bạn có lời khuyên nào để học tốt phần công thức tính độ dài vectơ và các kiến thức liên quan không?

Trả lời: Để học tốt phần này, bạn nên:

• Nắm vững lý thuyết: Hiểu rõ định nghĩa, công thức và các tính chất liên quan.
• Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng toán và rèn luyện kỹ năng.
• Sử dụng hình vẽ: Vẽ hình minh họa giúp bạn hình dung bài toán và tìm ra hướng giải.
• Trao đổi với bạn bè, thầy cô: Thảo luận, giải đáp thắc mắc và học hỏi kinh nghiệm từ người khác.
• Tìm kiếm tài liệu tham khảo: Đọc thêm sách, báo, tạp chí và các nguồn tài liệu trực tuyến để mở rộng kiến thức.

Lời khuyên từ tic.edu.vn: Hãy truy cập tic.edu.vn để khám phá kho tài liệu phong phú, đa dạng và được biên soạn kỹ lưỡng về vectơ, tọa độ và các chủ đề liên quan. tic.edu.vn cũng cung cấp các công cụ hỗ trợ học tập hiệu quả, giúp bạn nâng cao năng suất và đạt kết quả tốt nhất.

4.3. Nguồn Tài Liệu Tham Khảo

Câu hỏi: Bạn có thể giới thiệu một số nguồn tài liệu tham khảo hữu ích về chủ đề này không?

Trả lời: Dưới đây là một số nguồn tài liệu tham khảo hữu ích:

• Sách giáo khoa Toán lớp 12: Cung cấp kiến thức cơ bản và các bài tập vận dụng.
• Sách bài tập Toán lớp 12: Cung cấp nhiều bài tập luyện tập với các mức độ khó khác nhau.
• Các trang web học toán trực tuyến: Như Khan Academy, VietJack, ToanMath…
• Các diễn đàn, nhóm học tập trên mạng xã hội: Nơi bạn có thể trao đổi, thảo luận và học hỏi kinh nghiệm từ người khác.
• tic.edu.vn: Nguồn tài liệu học tập phong phú, đa dạng và được cập nhật liên tục.

Lời khuyên: Hãy lựa chọn các nguồn tài liệu phù hợp với trình độ và mục tiêu học tập của bạn. Đừng ngần ngại tìm kiếm sự giúp đỡ từ các nguồn tài liệu và cộng đồng học tập khi gặp khó khăn.

5. FAQ – Các Câu Hỏi Thường Gặp

5.1. Làm Thế Nào Để Ghi Nhớ Công Thức Tính Độ Dài Vectơ?

Câu hỏi: Làm thế nào để ghi nhớ công thức tính độ dài vectơ một cách hiệu quả?

Trả lời: Để ghi nhớ công thức tính độ dài vectơ hiệu quả, hãy hiểu rõ bản chất của công thức (xuất phát từ định lý Pytago), liên hệ với hình học trực quan, luyện tập thường xuyên và sử dụng các mẹo ghi nhớ.

5.2. Khi Nào Cần Sử Dụng Công Thức Tính Độ Dài Vectơ Trong Oxy Và Oxyz?

Câu hỏi: Khi nào thì nên sử dụng công thức tính độ dài vectơ trong mặt phẳng Oxy và khi nào thì nên sử dụng trong không gian Oxyz?

Trả lời: Sử dụng công thức trong Oxy khi bài toán liên quan đến hình học phẳng (2 chiều) và công thức trong Oxyz khi bài toán liên quan đến hình học không gian (3 chiều).

5.3. Có Thể Tính Độ Dài Vectơ Bằng Máy Tính Bỏ Túi Không?

Câu hỏi: Có thể sử dụng máy tính bỏ túi để tính độ dài vectơ không?

Trả lời: Có, hầu hết các máy tính bỏ túi hiện đại đều có chức năng tính căn bậc hai và các phép toán số học cơ bản, giúp bạn tính độ dài vectơ một cách nhanh chóng và chính xác.

5.4. Độ Dài Vectơ Có Thể Là Số Âm Không?

Câu hỏi: Độ dài của một vectơ có thể là một số âm không?

Trả lời: Không, độ dài vectơ luôn là một số không âm (lớn hơn hoặc bằng 0), vì nó biểu thị khoảng cách từ điểm đầu đến điểm cuối của vectơ.

5.5. Vectơ Không Có Độ Dài Bằng Bao Nhiêu?

Câu hỏi: Một vectơ không (vectơ có tất cả các thành phần bằng 0) có độ dài bằng bao nhiêu?

Trả lời: Vectơ không có độ dài bằng 0.

5.6. Tích Vô Hướng Có Liên Quan Gì Đến Góc Giữa Hai Vectơ?

Câu hỏi: Mối liên hệ giữa tích vô hướng và góc giữa hai vectơ là gì?

Trả lời: Tích vô hướng liên quan đến góc giữa hai vectơ thông qua công thức: $vec{a} cdot vec{b} = |vec{a}| cdot |vec{b}| cdot cos{theta}$. Từ đó, ta có thể tính góc giữa hai vectơ khi biết tích vô hướng và độ dài của chúng.

5.7. Làm Thế Nào Để Kiểm Tra Hai Vectơ Có Vuông Góc Với Nhau?

Câu hỏi: Làm thế nào để kiểm tra xem hai vectơ có vuông góc với nhau hay không?

Trả lời: Hai vectơ vuông góc với nhau khi và chỉ khi tích vô hướng của chúng bằng 0.

5.8. Ứng Dụng Của Tích Vô Hướng Trong Vật Lý Là Gì?

Câu hỏi: Tích vô hướng có những ứng dụng nào trong lĩnh vực vật lý?

Trả lời: Tích vô hướng có nhiều ứng dụng trong vật lý, chẳng hạn như tính công của lực, tính hình chiếu của vận tốc lên một phương nhất định và tính năng lượng.

5.9. Tại Sao Cần Học Công Thức Tính Độ Dài Vectơ?

Câu hỏi: Tại sao việc học công thức tính độ dài vectơ lại quan trọng?

Trả lời: Việc học công thức tính độ dài vectơ rất quan trọng vì nó là nền tảng để giải quyết các bài toán liên quan đến hình học, vật lý và kỹ thuật. Nó cũng giúp phát triển tư duy logic và khả năng giải quyết vấn đề.

5.10. Tôi Có Thể Tìm Thêm Bài Tập Về Vectơ Ở Đâu?

Câu hỏi: Tôi có thể tìm thêm bài tập về vectơ và các kiến thức liên quan ở đâu?

Trả lời: Bạn có thể tìm thêm bài tập trong sách giáo khoa, sách bài tập, các trang web học toán trực tuyến và trên tic.edu.vn.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, đa dạng và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi thử thách trên con đường học tập! Liên hệ với chúng tôi qua email: tic.edu@gmail.com hoặc truy cập trang web: tic.edu.vn để biết thêm chi tiết.