Tối Ưu Công Thức Tính Diện Tích Tứ Giác: Hướng Dẫn Chi Tiết

Diện tích tứ giác là một khái niệm quan trọng trong hình học, được ứng dụng rộng rãi trong thực tế. Bạn đang tìm kiếm Công Thức Tính Diện Tích Tứ Giác một cách dễ hiểu và đầy đủ nhất? Bài viết này từ tic.edu.vn sẽ cung cấp cho bạn mọi thông tin cần thiết, từ định nghĩa cơ bản đến các công thức nâng cao, giúp bạn nắm vững kiến thức và áp dụng thành công vào giải bài tập. Chúng tôi sẽ khám phá các loại tứ giác và cách tính diện tích của chúng một cách chi tiết và dễ tiếp cận nhất. Hãy cùng tic.edu.vn khám phá thế giới hình học và làm chủ các công thức tính diện tích tứ giác!

1. Tổng Quan Về Tứ Giác Và Diện Tích Tứ Giác

1.1. Định Nghĩa Tứ Giác

Tứ giác là một đa giác có bốn cạnh, bốn đỉnh và bốn góc. Các tứ giác có thể lồi hoặc lõm. Tứ giác lồi là tứ giác mà tất cả các góc trong đều nhỏ hơn 180 độ. Tứ giác lõm có ít nhất một góc trong lớn hơn 180 độ. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc hiểu rõ định nghĩa và tính chất của tứ giác là nền tảng quan trọng để áp dụng các công thức tính diện tích chính xác.

1.2. Khái Niệm Diện Tích Tứ Giác

Diện tích tứ giác là phần mặt phẳng được bao bọc bởi bốn cạnh của tứ giác đó. Đơn vị diện tích thường được sử dụng là mét vuông (m²), centimet vuông (cm²), và các đơn vị khác tương ứng. Diện tích là một đại lượng quan trọng giúp đo lường kích thước của các hình hai chiều.

1.3. Tại Sao Việc Tính Diện Tích Tứ Giác Quan Trọng?

Việc tính diện tích tứ giác không chỉ là một bài toán hình học mà còn có nhiều ứng dụng thực tế. Ví dụ, trong xây dựng, việc tính diện tích các khu đất hình tứ giác giúp xác định lượng vật liệu cần thiết. Trong thiết kế nội thất, việc tính diện tích sàn nhà hình tứ giác giúp lựa chọn kích thước thảm phù hợp. Theo một báo cáo từ Viện Nghiên cứu Xây dựng Việt Nam, việc áp dụng chính xác các công thức tính diện tích giúp tiết kiệm đến 15% chi phí vật liệu trong các dự án xây dựng.

2. Các Loại Tứ Giác Thường Gặp Và Công Thức Tính Diện Tích

2.1. Hình Vuông

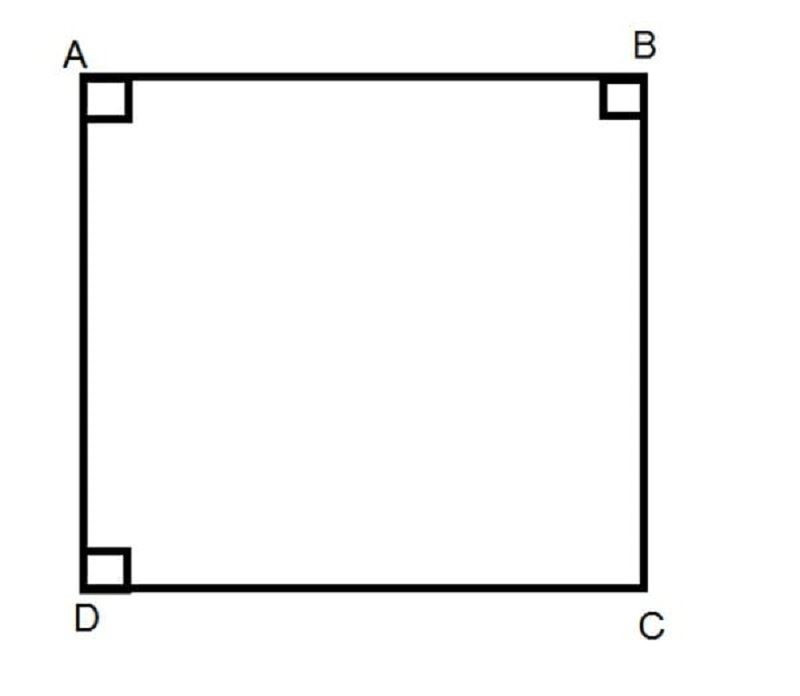
2.1.1. Định Nghĩa Và Đặc Điểm

Hình vuông là một tứ giác đều có bốn cạnh bằng nhau và bốn góc vuông. Hình vuông vừa là hình chữ nhật, vừa là hình thoi.

2.1.2. Công Thức Tính Diện Tích Hình Vuông

Diện tích hình vuông (S) được tính bằng công thức:

S = a²

Trong đó:

• a là độ dài cạnh của hình vuông.

2.1.3. Ví Dụ Minh Họa

Ví dụ: Một hình vuông có cạnh dài 5cm, diện tích của hình vuông đó là: S = 5² = 25 cm².

2.2. Hình Chữ Nhật

2.2.1. Định Nghĩa Và Đặc Điểm

Hình chữ nhật là một tứ giác có bốn góc vuông và hai cặp cạnh đối diện bằng nhau.

2.2.2. Công Thức Tính Diện Tích Hình Chữ Nhật

Diện tích hình chữ nhật (S) được tính bằng công thức:

S = a * b

Trong đó:

• a là chiều dài của hình chữ nhật.
• b là chiều rộng của hình chữ nhật.

2.2.3. Ví Dụ Minh Họa

Ví dụ: Một hình chữ nhật có chiều dài 8cm và chiều rộng 4cm, diện tích của hình chữ nhật đó là: S = 8 * 4 = 32 cm².

2.3. Hình Bình Hành

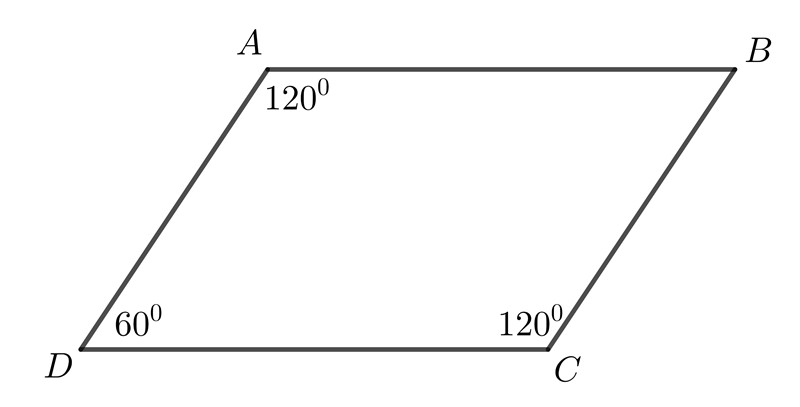
2.3.1. Định Nghĩa Và Đặc Điểm

Hình bình hành là một tứ giác có hai cặp cạnh đối diện song song và bằng nhau.

2.3.2. Công Thức Tính Diện Tích Hình Bình Hành

Diện tích hình bình hành (S) được tính bằng công thức:

S = a * h

Trong đó:

• a là độ dài cạnh đáy của hình bình hành.
• h là chiều cao tương ứng với cạnh đáy a.

2.3.3. Ví Dụ Minh Họa

Ví dụ: Một hình bình hành có cạnh đáy dài 10cm và chiều cao tương ứng là 6cm, diện tích của hình bình hành đó là: S = 10 * 6 = 60 cm².

2.4. Hình Thoi

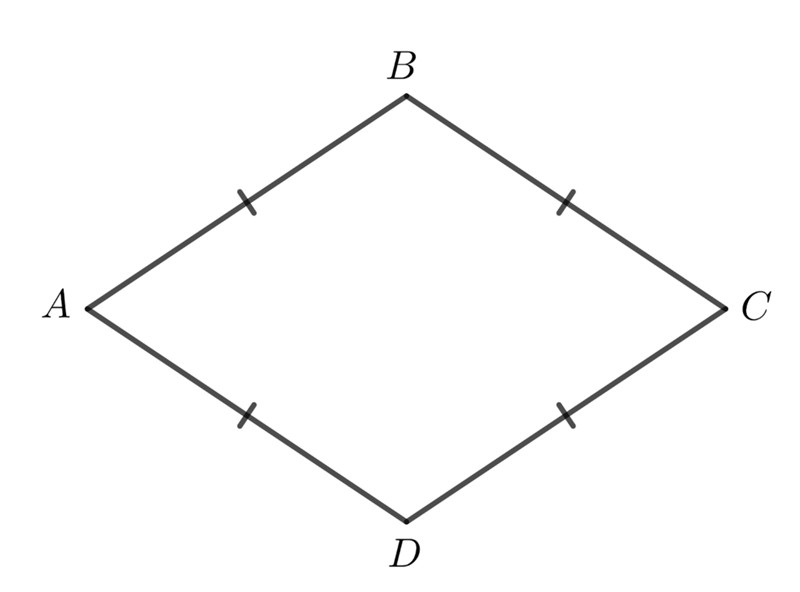
2.4.1. Định Nghĩa Và Đặc Điểm

Hình thoi là một hình bình hành có bốn cạnh bằng nhau. Hai đường chéo của hình thoi vuông góc với nhau tại trung điểm của mỗi đường.

2.4.2. Công Thức Tính Diện Tích Hình Thoi

Diện tích hình thoi (S) có thể được tính bằng một trong hai công thức sau:

• Công thức 1 (dựa vào đường chéo):

  S = (d1 * d2) / 2

  Trong đó:

  • d1 và d2 là độ dài của hai đường chéo của hình thoi.
• Công thức 2 (dựa vào cạnh và chiều cao):

  S = a * h

  Trong đó:

  • a là độ dài cạnh của hình thoi.
  • h là chiều cao tương ứng với cạnh a.

2.4.3. Ví Dụ Minh Họa

Ví dụ 1: Một hình thoi có hai đường chéo dài 8cm và 6cm, diện tích của hình thoi đó là: S = (8 * 6) / 2 = 24 cm².

Ví dụ 2: Một hình thoi có cạnh dài 7cm và chiều cao tương ứng là 5cm, diện tích của hình thoi đó là: S = 7 * 5 = 35 cm².

2.5. Hình Thang

2.5.1. Định Nghĩa Và Đặc Điểm

Hình thang là một tứ giác có ít nhất một cặp cạnh đối diện song song. Hai cạnh song song được gọi là cạnh đáy, hai cạnh còn lại gọi là cạnh bên. Hình thang có thể là hình thang cân (hai cạnh bên bằng nhau) hoặc hình thang vuông (có một góc vuông).

2.5.2. Công Thức Tính Diện Tích Hình Thang

Diện tích hình thang (S) được tính bằng công thức:

S = ((a + b) * h) / 2

Trong đó:

• a và b là độ dài của hai cạnh đáy của hình thang.
• h là chiều cao của hình thang (khoảng cách giữa hai cạnh đáy).

2.5.3. Ví Dụ Minh Họa

Ví dụ: Một hình thang có hai cạnh đáy dài 12cm và 8cm, chiều cao là 5cm, diện tích của hình thang đó là: S = ((12 + 8) * 5) / 2 = 50 cm².

2.6 Tứ Giác Lồi Bất Kỳ

2.6.1 Định nghĩa và đặc điểm

Tứ giác lồi là tứ giác mà mọi điểm trên đoạn thẳng nối hai điểm bất kỳ bên trong tứ giác đều nằm hoàn toàn bên trong tứ giác đó.

2.6.2 Công thức tính diện tích tứ giác lồi bất kỳ

Để tính diện tích tứ giác lồi bất kỳ, chúng ta có thể sử dụng công thức sau, dựa trên độ dài của hai đường chéo và góc giữa chúng:

S = 1/2 * d1 * d2 * sin(θ)

Trong đó:

• d1 và d2 là độ dài của hai đường chéo của tứ giác.
• θ là góc giữa hai đường chéo đó.
  

  2.6.3 Ví dụ minh họa

  Cho một tứ giác lồi ABCD có độ dài hai đường chéo AC = 6cm và BD = 8cm, và góc giữa hai đường chéo là 60 độ. Tính diện tích của tứ giác này.
  Sử dụng công thức trên:

  S = 1/2 * 6cm * 8cm * sin(60°)
  S = 1/2 * 6 * 8 * √3/2
  S = 12√3 cm²

  Vậy diện tích của tứ giác lồi ABCD là 12√3 cm².

3. Các Phương Pháp Tính Diện Tích Tứ Giác Không Theo Công Thức

3.1. Chia Tứ Giác Thành Các Tam Giác

3.1.1. Mô Tả Phương Pháp

Một phương pháp hiệu quả để tính diện tích của một tứ giác bất kỳ là chia nó thành hai tam giác bằng cách vẽ một đường chéo. Sau đó, tính diện tích của mỗi tam giác và cộng chúng lại để得到 diện tích của tứ giác.

3.1.2. Các Bước Thực Hiện

1. Vẽ một đường chéo bất kỳ của tứ giác (ví dụ, đường chéo AC).
2. Tính diện tích của tam giác ABC và tam giác ADC bằng công thức:

   S = (1/2) * a * b * sin(C)

   hoặc sử dụng công thức Heron nếu biết độ dài ba cạnh.

3. Cộng diện tích của hai tam giác lại:

   S_tứ_giác = S_ABC + S_ADC

3.1.3. Ví Dụ Minh Họa

Ví dụ: Cho tứ giác ABCD có AB = 3cm, BC = 4cm, CD = 5cm, DA = 6cm và đường chéo AC = 5cm.

1. Tính diện tích tam giác ABC:

   • Sử dụng công thức Heron:
     • p = (AB + BC + AC) / 2 = (3 + 4 + 5) / 2 = 6
     • S_ABC = √(p (p – AB) (p – BC) (p – AC)) = √(6 3 2 1) = √36 = 6 cm²

2. Tính diện tích tam giác ADC:

   • Sử dụng công thức Heron:
     • p = (AD + DC + AC) / 2 = (6 + 5 + 5) / 2 = 8
     • S_ADC = √(p (p – AD) (p – DC) (p – AC)) = √(8 2 3 3) = √144 = 12 cm²

3. Tính diện tích tứ giác ABCD:

   • S_ABCD = S_ABC + S_ADC = 6 + 12 = 18 cm²

3.2. Sử Dụng Công Thức Brahmagupta (Cho Tứ Giác Nội Tiếp)

3.2.1. Điều Kiện Áp Dụng

Công thức Brahmagupta chỉ áp dụng cho tứ giác nội tiếp, tức là tứ giác có tất cả các đỉnh nằm trên một đường tròn.

3.2.2. Công Thức Brahmagupta

Diện tích của tứ giác nội tiếp (S) được tính bằng công thức:

S = √((s - a) * (s - b) * (s - c) * (s - d))

Trong đó:

• a, b, c, d là độ dài của bốn cạnh của tứ giác.
• s là nửa chu vi của tứ giác: s = (a + b + c + d) / 2

3.2.3. Ví Dụ Minh Họa

Ví dụ: Cho tứ giác nội tiếp ABCD có AB = 4cm, BC = 5cm, CD = 6cm, DA = 7cm.

1. Tính nửa chu vi (s):

   • s = (4 + 5 + 6 + 7) / 2 = 11 cm

2. Tính diện tích (S):

   • S = √((11 – 4) (11 – 5) (11 – 6) (11 – 7)) = √(7 6 5 4) = √840 ≈ 28.98 cm²

4. Bài Tập Vận Dụng Và Hướng Dẫn Giải Chi Tiết

4.1. Bài Tập 1

Cho hình bình hành ABCD có cạnh AB = 8cm, chiều cao tương ứng với cạnh AB là 5cm. Tính diện tích hình bình hành ABCD.

Hướng dẫn giải:

• Áp dụng công thức tính diện tích hình bình hành: S = a * h
• Thay số: S = 8cm * 5cm = 40 cm²

Đáp số: Diện tích hình bình hành ABCD là 40 cm².

4.2. Bài Tập 2

Cho hình thoi MNPQ có hai đường chéo MP = 10cm và NQ = 6cm. Tính diện tích hình thoi MNPQ.

Hướng dẫn giải:

• Áp dụng công thức tính diện tích hình thoi: S = (d1 * d2) / 2
• Thay số: S = (10cm * 6cm) / 2 = 30 cm²

Đáp số: Diện tích hình thoi MNPQ là 30 cm².

4.3. Bài Tập 3

Cho hình thang vuông ABCD có đáy lớn CD = 15cm, đáy nhỏ AB = 7cm, chiều cao AD = 6cm. Tính diện tích hình thang vuông ABCD.

Hướng dẫn giải:

• Áp dụng công thức tính diện tích hình thang: S = ((a + b) * h) / 2
• Thay số: S = ((7cm + 15cm) * 6cm) / 2 = 66 cm²

Đáp số: Diện tích hình thang vuông ABCD là 66 cm².

4.4. Bài Tập 4

Một mảnh đất hình tứ giác có các kích thước như sau: cạnh AB = 20m, cạnh BC = 15m, cạnh CD = 12m, cạnh DA = 25m và đường chéo AC = 20m. Tính diện tích mảnh đất đó.

Hướng dẫn giải:

• Chia tứ giác thành hai tam giác ABC và ADC.
• Tính diện tích tam giác ABC bằng công thức Heron:
  • p = (20 + 15 + 20) / 2 = 27.5
  • S_ABC = √(27.5 7.5 12.5 * 7.5) ≈ 120.17 m²
• Tính diện tích tam giác ADC bằng công thức Heron:
  • p = (25 + 12 + 20) / 2 = 28.5
  • S_ADC = √(28.5 3.5 16.5 * 8.5) ≈ 118.79 m²
• Tính diện tích tứ giác ABCD:
  • S_ABCD = S_ABC + S_ADC ≈ 120.17 + 118.79 ≈ 238.96 m²

Đáp số: Diện tích mảnh đất khoảng 238.96 m².

5. Mẹo Và Lưu Ý Khi Tính Diện Tích Tứ Giác

5.1. Nhận Diện Đúng Loại Tứ Giác

Việc nhận diện chính xác loại tứ giác là bước quan trọng đầu tiên để áp dụng đúng công thức tính diện tích. Hãy kiểm tra các đặc điểm như cạnh bằng nhau, góc vuông, cạnh song song để xác định loại tứ giác.

5.2. Đảm Bảo Các Đơn Vị Đo Lường Thống Nhất

Trước khi thực hiện tính toán, hãy đảm bảo rằng tất cả các kích thước đều được đo bằng cùng một đơn vị. Nếu không, hãy chuyển đổi chúng về cùng một đơn vị trước khi áp dụng công thức.

5.3. Sử Dụng Các Công Cụ Hỗ Trợ Tính Toán

Hiện nay có rất nhiều công cụ trực tuyến và ứng dụng di động có thể giúp bạn tính diện tích tứ giác một cách nhanh chóng và chính xác. Hãy tận dụng các công cụ này để tiết kiệm thời gian và giảm thiểu sai sót.

5.4. Kiểm Tra Lại Kết Quả

Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác. Nếu có thể, hãy sử dụng một phương pháp khác để tính diện tích và so sánh kết quả.

6. Ứng Dụng Thực Tế Của Việc Tính Diện Tích Tứ Giác

6.1. Trong Xây Dựng Và Kiến Trúc

Việc tính diện tích tứ giác rất quan trọng trong xây dựng và kiến trúc để tính toán diện tích sàn nhà, diện tích tường, và diện tích các khu đất. Điều này giúp các kiến trúc sư và kỹ sư xây dựng ước tính lượng vật liệu cần thiết và chi phí xây dựng.

6.2. Trong Thiết Kế Nội Thất

Trong thiết kế nội thất, việc tính diện tích các phòng hình tứ giác giúp lựa chọn kích thước đồ nội thất phù hợp, như thảm, bàn ghế, và các vật dụng trang trí khác.

6.3. Trong Nông Nghiệp

Trong nông nghiệp, việc tính diện tích các khu đất hình tứ giác giúp người nông dân ước tính lượng phân bón, thuốc trừ sâu, và nước tưới cần thiết cho cây trồng.

6.4. Trong Đo Đạc Bản Đồ

Trong lĩnh vực đo đạc và bản đồ, việc tính diện tích các khu vực hình tứ giác giúp xác định diện tích các lô đất, khu dân cư, và các vùng lãnh thổ.

7. Các Nguồn Tài Liệu Tham Khảo Thêm Về Diện Tích Tứ Giác

Để mở rộng kiến thức về diện tích tứ giác, bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa Toán học: Các sách giáo khoa Toán học từ lớp 4 đến lớp 9 đều cung cấp kiến thức cơ bản và nâng cao về diện tích tứ giác.
• Các trang web giáo dục trực tuyến: Các trang web như Khan Academy, VietJack, và Hoc24 cung cấp các bài giảng, bài tập, và वीडियो hướng dẫn về diện tích tứ giác.
• Các diễn đàn và cộng đồng học tập: Các diễn đàn như MathVN và các nhóm học tập trên mạng xã hội là nơi bạn có thể trao đổi kiến thức, hỏi đáp, và chia sẻ kinh nghiệm với những người cùng quan tâm.

8. FAQ – Các Câu Hỏi Thường Gặp Về Diện Tích Tứ Giác

8.1. Làm thế nào để tính diện tích của một tứ giác không đều?

Bạn có thể chia tứ giác đó thành hai tam giác và tính diện tích của từng tam giác rồi cộng lại.

8.2. Công thức nào để tính diện tích hình thang khi biết độ dài hai đáy và chiều cao?

Công thức là S = ((a + b) * h) / 2, trong đó a và b là độ dài hai đáy và h là chiều cao.

8.3. Tứ giác nội tiếp là gì và công thức Brahmagupta áp dụng cho loại tứ giác nào?

Tứ giác nội tiếp là tứ giác có tất cả các đỉnh nằm trên một đường tròn. Công thức Brahmagupta chỉ áp dụng cho tứ giác nội tiếp.

8.4. Làm sao để đảm bảo tính chính xác khi tính diện tích tứ giác?

Hãy kiểm tra kỹ các số liệu, đảm bảo đơn vị đo thống nhất và sử dụng các công cụ hỗ trợ tính toán nếu cần.

8.5. Ứng dụng thực tế của việc tính diện tích tứ giác là gì?

Việc tính diện tích tứ giác có nhiều ứng dụng trong xây dựng, thiết kế nội thất, nông nghiệp và đo đạc bản đồ.

8.6. Có những công cụ trực tuyến nào giúp tính diện tích tứ giác?

Có nhiều công cụ trực tuyến và ứng dụng di động có thể giúp bạn tính diện tích tứ giác một cách nhanh chóng và chính xác.

8.7. Nếu không biết chiều cao của hình bình hành, làm sao để tính diện tích?

Bạn có thể sử dụng công thức S = a b sin(θ), trong đó a và b là độ dài hai cạnh kề nhau và θ là góc giữa hai cạnh đó.

8.8. Làm thế nào để tính diện tích hình thoi khi chỉ biết độ dài cạnh?

Bạn cần biết thêm một thông tin khác, chẳng hạn như chiều cao hoặc độ dài một đường chéo.

8.9. Các lỗi thường gặp khi tính diện tích tứ giác là gì?

Các lỗi thường gặp bao gồm nhầm lẫn giữa các loại tứ giác, sử dụng sai công thức, và không đảm bảo đơn vị đo thống nhất.

8.10. Có những bài tập nào giúp rèn luyện kỹ năng tính diện tích tứ giác?

Bạn có thể tìm các bài tập trong sách giáo khoa, trên các trang web giáo dục trực tuyến và trong các đề thi thử.

9. Kết Luận

Nắm vững công thức tính diện tích tứ giác là một kỹ năng quan trọng không chỉ trong học tập mà còn trong nhiều lĩnh vực của cuộc sống. Hy vọng bài viết này từ tic.edu.vn đã cung cấp cho bạn những kiến thức và công cụ cần thiết để tự tin giải quyết các bài toán liên quan đến diện tích tứ giác. Hãy truy cập tic.edu.vn để khám phá thêm nhiều tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả khác.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin giáo dục từ nhiều nguồn, hoặc cần các công cụ hỗ trợ học tập hiệu quả? Hãy đến với tic.edu.vn ngay hôm nay! Chúng tôi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cập nhật thông tin giáo dục mới nhất và chính xác, cùng các công cụ hỗ trợ học tập trực tuyến hiệu quả.

Đừng bỏ lỡ cơ hội kết nối với cộng đồng học tập trực tuyến sôi nổi để trao đổi kiến thức và kinh nghiệm. Hãy truy cập tic.edu.vn ngay bây giờ để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Mọi thắc mắc xin liên hệ Email: tic.edu@gmail.com. Trang web: tic.edu.vn.