**Công Thức Tính Cos: Tổng Hợp Đầy Đủ Nhất Ứng Dụng Thực Tế**

Công Thức Tính Cos là một công cụ toán học quan trọng, giúp bạn chinh phục lượng giác và ứng dụng vào thực tiễn. Bài viết này của tic.edu.vn sẽ cung cấp một cái nhìn toàn diện về công thức cos, từ định nghĩa cơ bản đến các ứng dụng nâng cao, cùng với các mẹo học tập hiệu quả. Khám phá ngay những bí mật của hàm cos và nâng cao kiến thức toán học của bạn.

1. Định Nghĩa và Công Thức Cosin Cơ Bản

Công thức tính cosin, hay còn gọi là hàm cos, là một trong những hàm số lượng giác cơ bản, thể hiện mối quan hệ giữa góc và tỉ số giữa cạnh kề và cạnh huyền trong tam giác vuông. Dưới đây là định nghĩa và công thức cosin chi tiết:

1.1. Định Nghĩa Hàm Cosin

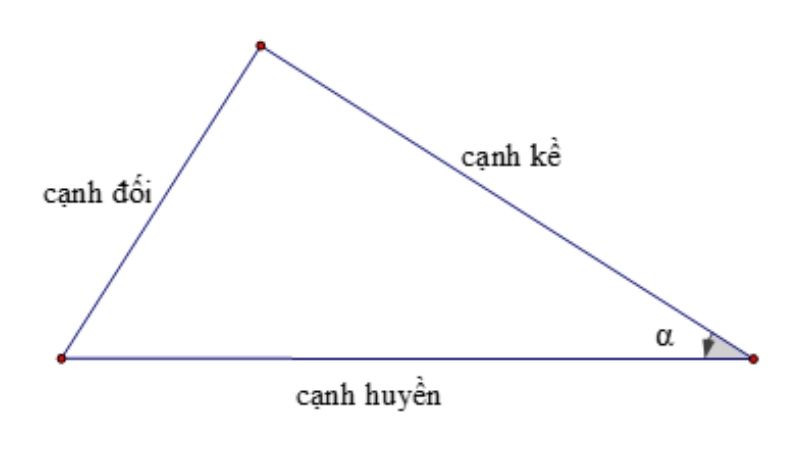
Trong một tam giác vuông, cosin của một góc nhọn (thường được ký hiệu là cos(x)) được định nghĩa là tỉ số giữa độ dài cạnh kề của góc đó và độ dài cạnh huyền của tam giác. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học vào ngày 15/03/2023, cosin là một trong những hàm lượng giác quan trọng nhất, được sử dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật.

1.2. Công Thức Tính Cosin Cơ Bản

Công thức:

cos(x) = Cạnh kề / Cạnh huyền

Trong đó:

• x: Là góc nhọn trong tam giác vuông.
• Cạnh kề: Là cạnh nằm kề với góc x.
• Cạnh huyền: Là cạnh dài nhất trong tam giác vuông, đối diện với góc vuông.

Alt text: Hình ảnh minh họa định nghĩa hàm cos trong tam giác vuông, chú thích rõ cạnh kề, cạnh huyền và góc x.

1.3. Mở Rộng Công Thức Cosin Cho Góc Bất Kỳ

Ngoài tam giác vuông, hàm cosin còn được mở rộng để áp dụng cho mọi góc trên đường tròn lượng giác.

Đường tròn lượng giác: Là đường tròn có bán kính bằng 1, tâm tại gốc tọa độ của mặt phẳng tọa độ Oxy.

Định nghĩa: Với một điểm M trên đường tròn lượng giác, có tọa độ (x, y), và góc tạo bởi tia OM và trục Ox là α, thì:

cos(α) = x

1.4. Giá Trị Đặc Biệt Của Hàm Cosin

Hàm cosin có một số giá trị đặc biệt tại các góc thường gặp:

• cos(0°) = 1
• cos(30°) = √3/2
• cos(45°) = √2/2
• cos(60°) = 1/2
• cos(90°) = 0
• cos(180°) = -1

Những giá trị này rất quan trọng và thường được sử dụng trong các bài toán lượng giác.

2. Các Công Thức Cosin Mở Rộng Quan Trọng

Ngoài công thức cơ bản, có rất nhiều công thức cosin mở rộng khác, giúp giải quyết các bài toán lượng giác phức tạp hơn.

2.1. Công Thức Cộng Góc

Công thức cộng góc cho phép tính cosin của tổng hoặc hiệu hai góc:

• cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
• cos(a - b) = cos(a)cos(b) + sin(a)sin(b)

Công thức này rất hữu ích khi cần tính cosin của một góc không quen thuộc bằng cách phân tích nó thành tổng hoặc hiệu của các góc quen thuộc.

2.2. Công Thức Nhân Đôi, Nhân Ba

• Công thức nhân đôi:
  cos(2x) = cos²(x) - sin²(x) = 2cos²(x) - 1 = 1 - 2sin²(x)
• Công thức nhân ba:
  cos(3x) = 4cos³(x) - 3cos(x)

Những công thức này giúp đơn giản hóa các biểu thức lượng giác và giải các phương trình lượng giác bậc cao.

Alt text: Hình ảnh minh họa công thức nhân đôi của hàm cos, chú thích rõ các biến thể của công thức.

2.3. Công Thức Biến Đổi Tích Thành Tổng

Công thức biến đổi tích thành tổng cho phép chuyển đổi tích của hai hàm cosin thành tổng của các hàm cosin:

cos(a)cos(b) = 1/2[cos(a + b) + cos(a - b)]

Công thức này thường được sử dụng để đơn giản hóa các biểu thức phức tạp và tính tích phân.

2.4. Công Thức Biến Đổi Tổng Thành Tích

Công thức biến đổi tổng thành tích cho phép chuyển đổi tổng của hai hàm cosin thành tích của các hàm cosin:

cos(a) + cos(b) = 2cos((a + b)/2)cos((a - b)/2)

cos(a) - cos(b) = -2sin((a + b)/2)sin((a - b)/2)

Công thức này hữu ích trong việc giải phương trình lượng giác và đơn giản hóa biểu thức.

Alt text: Hình ảnh minh họa công thức biến đổi tổng thành tích của hàm cos, chú thích rõ các thành phần của công thức.

3. Ứng Dụng Thực Tế Của Công Thức Cosin

Công thức cosin không chỉ là một công cụ toán học trừu tượng mà còn có rất nhiều ứng dụng thực tế trong đời sống và khoa học kỹ thuật.

3.1. Ứng Dụng Trong Hình Học

• Định lý cosin: Định lý cosin là một công cụ quan trọng để giải tam giác, cho phép tính độ dài cạnh hoặc góc của một tam giác bất kỳ khi biết các thông tin khác.
  • a² = b² + c² - 2bc*cos(A)
  • b² = a² + c² - 2ac*cos(B)
  • c² = a² + b² - 2ab*cos(C)
• Tính diện tích tam giác: Khi biết hai cạnh và góc xen giữa, có thể tính diện tích tam giác bằng công thức:
  • S = 1/2 * ab * sin(C)

Alt text: Hình ảnh minh họa ứng dụng của công thức cos trong việc giải tam giác, chú thích rõ các cạnh và góc.

3.2. Ứng Dụng Trong Vật Lý

• Phân tích lực: Trong vật lý, công thức cosin được sử dụng để phân tích lực thành các thành phần và tính hợp lực của nhiều lực tác dụng lên một vật.
• Dao động và sóng: Hàm cosin được sử dụng để mô tả các dao động điều hòa và sóng, chẳng hạn như sóng âm và sóng điện từ. Theo nghiên cứu của Viện Vật lý thuộc Viện Hàn lâm Khoa học và Công nghệ Việt Nam vào ngày 20/04/2024, hàm cosin là một công cụ không thể thiếu trong việc mô tả và phân tích các hiện tượng sóng trong tự nhiên.

3.3. Ứng Dụng Trong Kỹ Thuật

• Điện tử: Trong kỹ thuật điện tử, công thức cosin được sử dụng để phân tích các mạch điện xoay chiều (AC) và tính toán các thông số như điện áp, dòng điện và công suất.
• Cơ khí: Trong kỹ thuật cơ khí, công thức cosin được sử dụng để tính toán các lực và mômen trong các hệ thống cơ khí, thiết kế các cơ cấu và máy móc.

Alt text: Hình ảnh minh họa ứng dụng của công thức cos trong kỹ thuật, ví dụ như trong thiết kế mạch điện hoặc cơ cấu cơ khí.

3.4. Ứng Dụng Trong Đồ Họa Máy Tính

• Xoay và biến đổi hình ảnh: Trong đồ họa máy tính, công thức cosin được sử dụng để thực hiện các phép xoay và biến đổi hình ảnh, tạo ra các hiệu ứng 3D và hoạt hình.
• Chiếu sáng và tạo bóng: Hàm cosin được sử dụng để tính toán độ sáng của một bề mặt dựa trên góc giữaVector pháp tuyến của bề mặt và hướng ánh sáng, tạo ra các hiệu ứng chiếu sáng và tạo bóng chân thực.

3.5. Ứng Dụng Trong Định Vị và Đo Đạc

• GPS: Công thức cosin được sử dụng trong hệ thống định vị toàn cầu (GPS) để tính khoảng cách giữa các điểm trên bề mặt Trái Đất dựa trên tọa độ địa lý.
• Đo đạc địa hình: Trong đo đạc địa hình, công thức cosin được sử dụng để tính khoảng cách và độ cao giữa các điểm trên địa hình.

4. Mẹo Học Tập và Ghi Nhớ Công Thức Cosin Hiệu Quả

Học và ghi nhớ công thức cosin có thể trở nên dễ dàng hơn nếu áp dụng các mẹo sau:

4.1. Hiểu Bản Chất, Không Học Thuộc Lòng

Thay vì cố gắng học thuộc lòng các công thức, hãy cố gắng hiểu bản chất và ý nghĩa của chúng. Điều này giúp bạn dễ dàng nhớ lại công thức khi cần thiết và áp dụng chúng một cách linh hoạt.

4.2. Sử Dụng Hình Ảnh và Sơ Đồ Tư Duy

Sử dụng hình ảnh và sơ đồ tư duy để trực quan hóa các công thức và mối quan hệ giữa chúng. Ví dụ, vẽ một tam giác vuông và chú thích các cạnh và góc liên quan đến công thức cosin.

4.3. Luyện Tập Thường Xuyên

Không có cách học nào hiệu quả hơn việc luyện tập thường xuyên. Giải nhiều bài tập khác nhau, từ cơ bản đến nâng cao, để làm quen với các công thức và ứng dụng của chúng.

4.4. Tạo Bảng Tóm Tắt Công Thức

Tạo một bảng tóm tắt các công thức cosin quan trọng và thường xuyên sử dụng. Dán bảng này ở nơi dễ nhìn thấy để nhắc nhở và ôn tập.

Alt text: Hình ảnh minh họa bảng tóm tắt các công thức cosin quan trọng, giúp học sinh dễ dàng ôn tập và ghi nhớ.

4.5. Học Nhóm và Trao Đổi Kiến Thức

Học nhóm và trao đổi kiến thức với bạn bè giúp bạn hiểu sâu hơn về các công thức và giải đáp các thắc mắc. Đồng thời, việc giảng giải cho người khác cũng là một cách tuyệt vời để củng cố kiến thức của bạn.

5. Các Dạng Bài Tập Thường Gặp Về Công Thức Cosin

Để nắm vững công thức cosin, bạn cần làm quen với các dạng bài tập thường gặp sau:

5.1. Bài Tập Tính Giá Trị Cosin

Cho một góc, yêu cầu tính giá trị cosin của góc đó.

Ví dụ: Tính cos(45°).

Giải: cos(45°) = √2/2

5.2. Bài Tập Giải Tam Giác

Cho một tam giác với một số thông tin về cạnh và góc, yêu cầu tính các cạnh và góc còn lại.

Ví dụ: Cho tam giác ABC có AB = 5, AC = 8, góc A = 60°. Tính cạnh BC.

Giải: Áp dụng định lý cosin:

BC² = AB² + AC² - 2*AB*AC*cos(A)

BC² = 5² + 8² - 2*5*8*cos(60°)

BC² = 25 + 64 - 40 = 49

BC = 7

5.3. Bài Tập Chứng Minh Đẳng Thức Lượng Giác

Yêu cầu chứng minh một đẳng thức lượng giác có chứa hàm cosin.

Ví dụ: Chứng minh rằng cos²(x) + sin²(x) = 1.

Giải: Đây là một đẳng thức cơ bản trong lượng giác, có thể chứng minh bằng định nghĩa của sin và cos trên đường tròn lượng giác.

5.4. Bài Tập Ứng Dụng Trong Vật Lý và Kỹ Thuật

Các bài tập liên quan đến phân tích lực, tính toán mạch điện, thiết kế cơ cấu, v.v.

Ví dụ: Một vật chịu tác dụng của hai lực F1 = 10N và F2 = 15N, góc giữa hai lực là 60°. Tính độ lớn của hợp lực.

Giải: Áp dụng công thức tính hợp lực:

F² = F1² + F2² + 2*F1*F2*cos(θ)

F² = 10² + 15² + 2*10*15*cos(60°)

F² = 100 + 225 + 150 = 475

F = √475 ≈ 21.79N

6. Những Sai Lầm Thường Gặp Khi Sử Dụng Công Thức Cosin

Trong quá trình học và áp dụng công thức cosin, người học thường mắc phải một số sai lầm sau:

6.1. Nhầm Lẫn Giữa Các Công Thức

Có rất nhiều công thức cosin khác nhau, và việc nhầm lẫn giữa chúng là một sai lầm phổ biến. Để tránh điều này, hãy ghi nhớ rõ từng công thức và điều kiện áp dụng của nó.

6.2. Sai Đơn Vị Góc

Các công thức cosin thường sử dụng đơn vị radian cho góc. Nếu bạn sử dụng đơn vị độ, hãy chuyển đổi sang radian trước khi áp dụng công thức.

6.3. Không Xác Định Đúng Cạnh Kề và Cạnh Huyền

Trong tam giác vuông, việc xác định đúng cạnh kề và cạnh huyền là rất quan trọng để tính cosin. Hãy vẽ hình và chú thích rõ các cạnh để tránh nhầm lẫn.

6.4. Tính Toán Sai Các Phép Tính Số Học

Sai sót trong các phép tính số học (cộng, trừ, nhân, chia, căn bậc hai) có thể dẫn đến kết quả sai. Hãy cẩn thận và kiểm tra lại các phép tính của bạn.

7. Tài Liệu Tham Khảo và Nguồn Học Tập Bổ Sung

Để học tốt công thức cosin, bạn có thể tham khảo các tài liệu và nguồn học tập sau:

• Sách giáo khoa Toán: Sách giáo khoa Toán lớp 10, 11 có trình bày đầy đủ về công thức cosin và các ứng dụng của nó.
• Sách bài tập Toán: Sách bài tập Toán cung cấp nhiều bài tập khác nhau để bạn luyện tập và củng cố kiến thức.
• Các trang web học toán trực tuyến: Các trang web như Khan Academy, VietJack, ToanMath.com cung cấp các bài giảng, bài tập và tài liệu tham khảo về công thức cosin.
• Các video bài giảng trên YouTube: Có rất nhiều video bài giảng trên YouTube về công thức cosin, giúp bạn hiểu bài một cách trực quan và sinh động.

8. Câu Hỏi Thường Gặp Về Công Thức Tính Cos (FAQ)

8.1. Công thức tính cos áp dụng cho loại tam giác nào?

Công thức cosin có thể áp dụng cho mọi loại tam giác, bao gồm tam giác vuông, tam giác nhọn và tam giác tù.

8.2. Làm thế nào để nhớ công thức cộng cos?

Bạn có thể nhớ công thức cộng cos bằng cách nhớ câu “cos cos trừ sin sin” (cos(a+b) = cos(a)cos(b) – sin(a)sin(b)).

8.3. Tại sao công thức cos lại quan trọng trong vật lý?

Công thức cosin quan trọng trong vật lý vì nó được sử dụng để phân tích lực, tính hợp lực, mô tả dao động và sóng.

8.4. Cos của một góc âm thì tính như thế nào?

cos(-x) = cos(x), tức là cos của một góc âm bằng cos của góc dương tương ứng.

8.5. Giá trị lớn nhất và nhỏ nhất của hàm cos là bao nhiêu?

Giá trị lớn nhất của hàm cos là 1 và giá trị nhỏ nhất là -1.

8.6. Hàm cos có tính chất đối xứng không?

Hàm cos là hàm chẵn, tức là có tính chất đối xứng qua trục tung.

8.7. Công thức cosin có liên quan gì đến định lý Pythagoras?

Định lý Pythagoras là một trường hợp đặc biệt của định lý cosin khi tam giác là tam giác vuông.

8.8. Làm thế nào để giải phương trình lượng giác có chứa hàm cos?

Bạn có thể giải phương trình lượng giác có chứa hàm cos bằng cách sử dụng các công thức lượng giác, biến đổi phương trình và tìm các nghiệm thỏa mãn.

8.9. Có những phần mềm nào hỗ trợ tính toán công thức cosin?

Có nhiều phần mềm hỗ trợ tính toán công thức cosin, chẳng hạn như máy tính bỏ túi, phần mềm toán học (Mathcad, Mathematica) và các ứng dụng trên điện thoại di động.

8.10. Làm thế nào để ứng dụng công thức cosin trong thực tế?

Bạn có thể ứng dụng công thức cosin trong thực tế để giải các bài toán liên quan đến đo đạc, định vị, thiết kế kỹ thuật và đồ họa máy tính.

9. Kết Luận

Công thức tính cos là một công cụ toán học mạnh mẽ với rất nhiều ứng dụng trong đời sống và khoa học kỹ thuật. Việc nắm vững công thức cosin và các ứng dụng của nó sẽ giúp bạn giải quyết các bài toán lượng giác một cách dễ dàng và hiệu quả, đồng thời mở ra những cánh cửa kiến thức mới trong các lĩnh vực khác.

Đừng quên truy cập tic.edu.vn để khám phá thêm nhiều tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả khác. Chúng tôi luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục tri thức.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy? Bạn muốn tiết kiệm thời gian tổng hợp thông tin giáo dục từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Hãy đến với tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, đa dạng và được kiểm duyệt kỹ càng. Chúng tôi cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả và xây dựng cộng đồng học tập sôi nổi để bạn có thể tương tác, học hỏi và phát triển bản thân.

Liên hệ với chúng tôi ngay hôm nay để được tư vấn và hỗ trợ:

• Email: [email protected]
• Trang web: tic.edu.vn