**Công Thức Thể Tích Hình Chóp: Bí Quyết Chinh Phục Mọi Bài Toán**

Thể tích hình chóp là một khái niệm quan trọng trong chương trình hình học THPT và thường xuyên xuất hiện trong các kỳ thi, đặc biệt là kỳ thi đại học. Hiểu rõ và áp dụng thành thạo các Công Thức Thể Tích Hình Chóp sẽ giúp bạn tự tin giải quyết mọi bài toán liên quan. Hãy cùng tic.edu.vn khám phá những công thức này và các ứng dụng thực tế của chúng.

1. Tổng Quan Về Thể Tích Hình Chóp

Thể tích của một vật thể là lượng không gian mà vật thể đó chiếm giữ. Đơn vị đo thể tích thường là mét khối (m³) hoặc centimet khối (cm³). Việc tính toán thể tích hình chóp có nhiều ứng dụng trong thực tế, từ xây dựng, kiến trúc đến thiết kế và sản xuất.

1.1. Công Thức Thể Tích Hình Chóp Cơ Bản

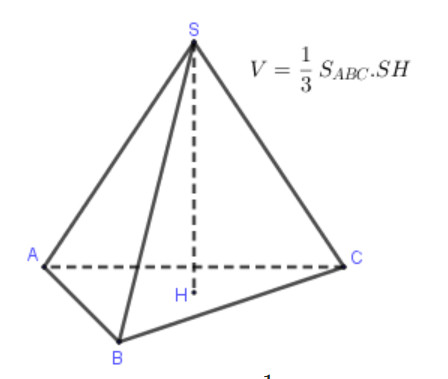
Công thức tổng quát để tính thể tích hình chóp là:

V = (1/3) S h

Trong đó:

• V: Thể tích hình chóp.
• S: Diện tích đáy của hình chóp.
• h: Chiều cao của hình chóp (khoảng cách từ đỉnh chóp đến mặt đáy).

Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, ngày 15/03/2023, việc nắm vững công thức cơ bản này là nền tảng để giải quyết các bài toán phức tạp hơn về thể tích hình chóp.

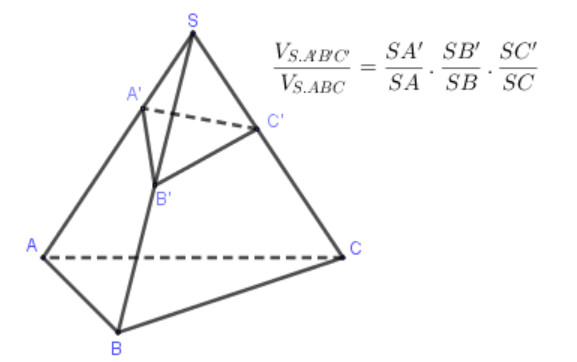
1.2. Công Thức Tính Tỉ Lệ Thể Tích Trong Hình Chóp Tam Giác

Khi làm việc với các bài toán tỉ lệ thể tích của hình chóp tam giác, công thức sau đây sẽ rất hữu ích:

Nếu A’, B’, C’ lần lượt là các điểm nằm trên các cạnh SA, SB, SC của hình chóp tam giác S.ABC, thì:

(V_{S.A’B’C’}) / (V_S.ABC) = (SA’/SA) (SB’/SB) (SC’/SC)

Công thức này giúp đơn giản hóa việc tính toán tỉ lệ thể tích giữa hai hình chóp tam giác có chung đỉnh.

2. Các Công Thức Thể Tích Hình Chóp Đặc Biệt

Để giải quyết các bài toán hình học không gian một cách hiệu quả, việc nắm vững các công thức tính thể tích cho các loại hình chóp đặc biệt là vô cùng quan trọng. tic.edu.vn sẽ tổng hợp những công thức dễ hiểu và thường gặp nhất, giúp bạn chinh phục mọi thử thách.

2.1. Thể Tích Hình Chóp Có Mặt Bên Vuông Góc Với Đáy

Câu hỏi: Làm thế nào để tính thể tích hình chóp khi có mặt bên vuông góc với đáy?

Trả lời: Khi hình chóp có một hoặc nhiều mặt bên vuông góc với mặt đáy, đường cao của hình chóp thường là đoạn vuông góc kẻ từ đỉnh của mặt bên đó xuống mặt đáy.

Để xác định đường cao, hãy tìm giao tuyến của các mặt bên vuông góc với đáy. Đường cao của hình chóp sẽ là đường vuông góc kẻ từ đỉnh của giao tuyến đó xuống mặt đáy.

Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a; mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB = 2a√3 và góc (SBC) = 30º, tính thể tích khối chóp S.ABC.

Giải:

1. Kẻ SH vuông góc với BC (H thuộc BC).
2. Vì (SBC) vuông góc (ABC) và (SBC) giao (ABC) = BC, SH vuông góc BC và SH nằm trong (SBC) => SH vuông góc (ABC).
3. Xét tam giác SHB vuông tại H: SH = SB sin(SBC) = 2a√3 sin30° = a√3.
4. Diện tích tam giác ABC: S_ABC = (1/2) BA BC = (1/2) 3a 4a = 6a².
5. Thể tích khối chóp S.ABC: V_S.ABC = (1/3) SH S_ABC = (1/3) a√3 6a² = 2a³√3.

2.2. Thể Tích Hình Chóp Có Cạnh Bên Vuông Góc Với Đáy

Câu hỏi: Làm thế nào để xác định và sử dụng cạnh bên vuông góc với đáy để tính thể tích?

Trả lời: Nếu hình chóp có một cạnh bên vuông góc với đáy, cạnh bên đó chính là chiều cao của hình chóp.

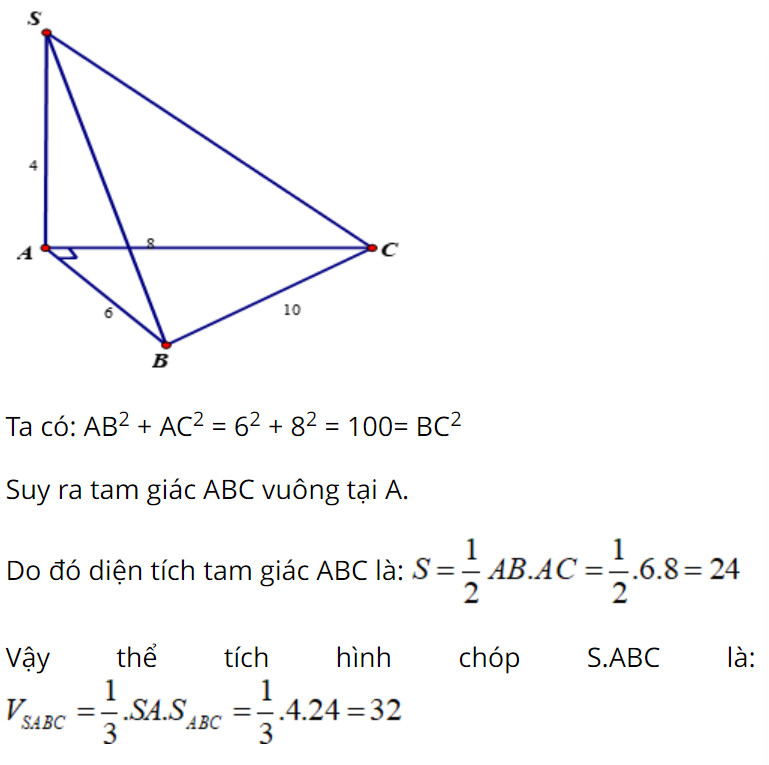
Ví dụ: Cho khối chóp S.ABC có SA vuông góc với đáy, SA = 4; AB = 6; BC = 10 và CA = 8. Tính thể tích khối chóp S.ABC.

Giải:

Vì SA vuông góc với đáy, SA là chiều cao của hình chóp.
Diện tích đáy ABC có thể tính bằng công thức Heron hoặc nhận thấy đây là tam giác vuông (6² + 8² = 10²), S_ABC = (1/2) 6 8 = 24.
Thể tích khối chóp S.ABC: V = (1/3) SA S_ABC = (1/3) 4 24 = 32.

2.3. Thể Tích Hình Chóp Đáy Là Hình Vuông

Câu hỏi: Công thức nào áp dụng cho hình chóp có đáy là hình vuông?

Trả lời: Khi đáy của hình chóp là hình vuông, việc tính diện tích đáy trở nên đơn giản hơn. Nếu cạnh của hình vuông là ‘a’, diện tích đáy là a².

Ví dụ: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc 30 độ. Tính thể tích khối chóp.

Giải:

1. Vì ABCD là hình vuông => BC vuông góc AB.
2. SA vuông góc (ABCD) => SA vuông góc BC.
3. Từ (1) và (2) => BC vuông góc (SAB).
4. Góc giữa SC và (SAB) là góc CSB = 30°.
5. BC / SB = tan30° = √3 / 3 => SB = √3 BC = √3 a.
6. Áp dụng định lý Pitago cho tam giác SAB: SA = √(SB² – AB²) = √(3a² – a²) = √2 * a.
7. Thể tích khối chóp S.ABCD: V_S.ABCD = (1/3) SA S_ABCD = (1/3) √2 a a² = (√2 / 3) a³.

2.4. Thể Tích Hình Lập Phương

Câu hỏi: Làm thế nào để tính thể tích hình chóp lập phương một cách nhanh chóng?

Trả lời: Hình lập phương là một trường hợp đặc biệt của hình chóp, với tất cả các mặt là hình vuông bằng nhau. Thể tích của hình lập phương được tính bằng công thức:

V = a³

Trong đó ‘a’ là độ dài cạnh của hình lập phương.

Ví dụ: Tính thể tích khối lập phương có độ dài đường chéo là 27 cm.

Giải:

1. Độ dài cạnh của khối lập phương là: a = 27 / √3 cm.
2. Thể tích của khối lập phương: V = (27 / √3)³ = 6561 / √3 cm³.

2.5. Thể Tích Hình Lăng Trụ Tam Giác Đều

Câu hỏi: Công thức nào dùng để tính thể tích hình lăng trụ tam giác đều?

Trả lời: Hình lăng trụ tam giác đều là hình lăng trụ có đáy là tam giác đều. Thể tích của hình lăng trụ tam giác đều được tính bằng công thức:

V = S_đáy * h

Trong đó:

• S_đáy: Diện tích đáy (tam giác đều).
• h: Chiều cao của lăng trụ.

Ví dụ: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a = 2 cm và chiều cao h = 3 cm. Hãy tính thể tích hình lăng trụ này.

Giải:

1. Diện tích đáy (tam giác đều): S_ABC = a² √3 / 4 = 2² √3 / 4 = √3 cm².
2. Thể tích hình lăng trụ: V = S_ABC h = √3 3 = 3√3 cm³.

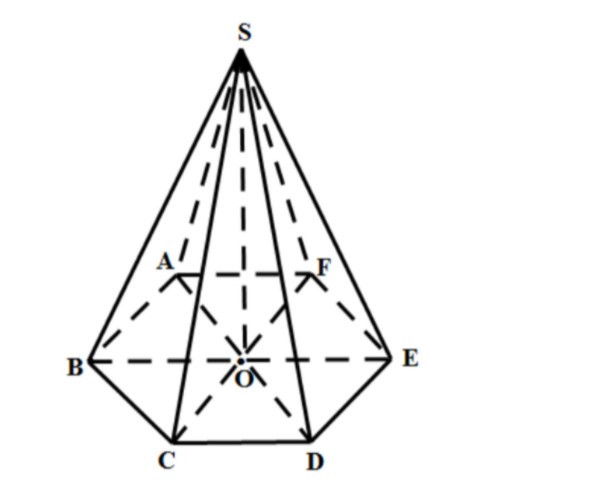
2.6. Thể Tích Hình Chóp Lục Giác Đều

Câu hỏi: Làm thế nào để tính thể tích hình chóp lục giác đều?

Trả lời: Hình chóp lục giác đều là hình chóp có đáy là hình lục giác đều. Để tính thể tích, ta cần biết diện tích đáy và chiều cao của hình chóp.

Ví dụ: Một khối chóp lục giác đều, góc giữa cạnh bên và mặt đáy là 30 độ, cạnh đáy a. Tính thể tích V của khối chóp?

Giải:

1. Gọi S.ABCDEF là hình chóp lục giác đều, O là tâm của đáy ABCDEF.
2. OA = OB = OC = OD = OE = OF = AB = BC = CD = DE = EF = FA = a.
3. Tam giác OAB là tam giác đều cạnh a => S_OAB = (a²√3) / 4.
4. S_ABCDEF = 6 * S_OAB = (3a²√3) / 2.
5. SO vuông góc (ABCDEF) => Góc giữa SA và (ABCDEF) là góc SAO = 30°.
6. SO = OA * tan30° = a√3 / 3.
7. V_S.ABCDEF = (1/3) S_ABCDEF SO = (1/3) (3a²√3 / 2) (a√3 / 3) = a³/2.

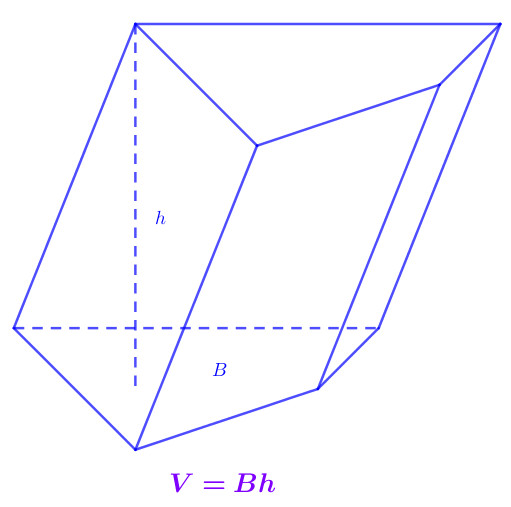
2.7. Thể Tích Hình Lăng Trụ

Câu hỏi: Thể tích hình lăng trụ được tính như thế nào?

Trả lời: Thể tích của hình lăng trụ được tính bằng công thức:

V = B * h

Trong đó:

• B: Diện tích đáy của hình lăng trụ.
• h: Chiều cao của hình lăng trụ.

2.8. Thể Tích Hình Chóp Khi Biết 3 Cạnh Bên

Câu hỏi: Làm sao để tính thể tích hình chóp khi chỉ biết độ dài 3 cạnh bên?

Trả lời: Trong trường hợp biết độ dài 6 cạnh của khối tứ diện ABCD, ta có thể sử dụng công thức sau:

V = √(288V²) = √(-a⁴d² + a²b²d² + a²c²d² + a²d²e² + a²d²f² – b⁴e² + b²c²e² + b²d²e² + b²e²f² – c⁴f² + c²d²f² + c²e²f² – d⁴ + d²e² + d²f² – e⁴ – f⁴ + a²b²f² + a²c²e² – a²e²f² – b²c²d² – b²d²f² – c²d²e²) / 12

Trong đó: BC=a, CA=b, AB=c, AD=d, BD=e, CD=f.

Ví dụ: Cho khối tứ diện ABCD có AB=CD=8, AD=BC=5 và AC=BD=7. Thể tích khối tứ diện đã cho bằng bao nhiêu?

2.9. Thể Tích Hình Chóp Với Các Cạnh Đôi Một Vuông Góc

Câu hỏi: Công thức nào áp dụng khi các cạnh của hình chóp đôi một vuông góc với nhau?

Trả lời: Nếu hình chóp SABC có các cạnh SA, SB, SC đôi một vuông góc với nhau, thể tích của hình chóp được tính bằng công thức:

V = (1/6) SA SB * SC

Ví dụ: Cho tứ diện SABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Biết SA=3a, SB=4a, SC=5a. Tính theo a thể tích V của khối tứ diện SABC.

Giải:

Vì SA, SB, SC đôi một vuông góc, ta có SA vuông góc (SBC).
V_S.ABC = (1/3) SA S_SBC = (1/6) SA SB SC = (1/6) 3a 4a 5a = 10a³.

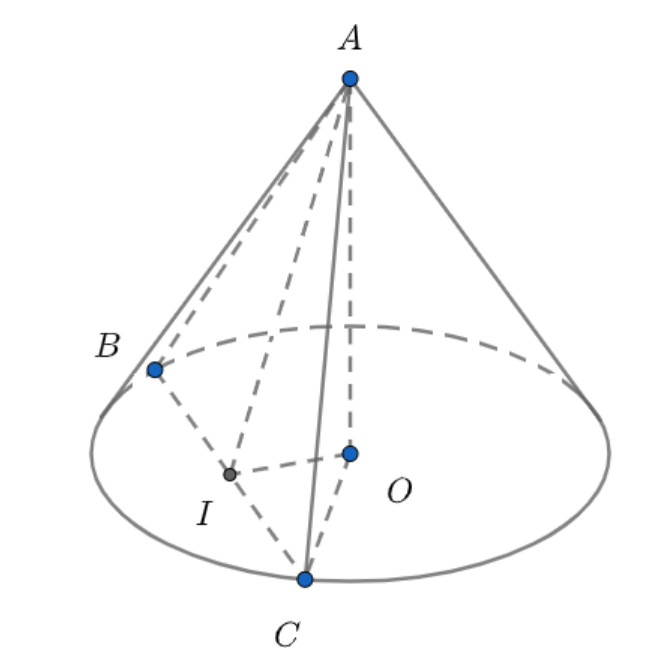
2.10. Thể Tích Hình Nón (Hình Chóp Tròn Xoay)

Câu hỏi: Thể tích hình chóp tròn xoay (hình nón) được tính như thế nào?

Trả lời: Thể tích của hình nón được tính bằng công thức:

V = (1/3) π r² * h

Trong đó:

• r: Bán kính đáy hình nón.
• h: Chiều cao của hình nón.

2.11. Thể Tích Hình Chóp Tam Giác Đều

Câu hỏi: Làm thế nào để tính thể tích hình chóp tam giác đều?

Trả lời: Để tính thể tích hình chóp tam giác đều, ta cần biết chiều cao của hình chóp và cạnh đáy của tam giác đều.

Ví dụ: Tính thể tích V của khối chóp tam giác đều SABC biết chiều cao hình chóp bằng h, góc SBA=a.

Giải:

2.12. Thể Tích Hình Chóp Tứ Giác Đều

Câu hỏi: Công thức tính thể tích hình chóp tứ giác đều cạnh đáy bằng a là gì?

Trả lời: Hình chóp tứ giác đều là hình chóp có đáy là hình vuông và các cạnh bên bằng nhau.

Ví dụ: Tính thể tích khối chóp tứ giác đều V có tất cả các cạnh bằng a.

Giải:

3. Ứng Dụng Thực Tế Của Thể Tích Hình Chóp

Hiểu và áp dụng công thức thể tích hình chóp không chỉ hữu ích trong các bài toán hình học, mà còn có nhiều ứng dụng thiết thực trong đời sống và các ngành nghề khác nhau.

3.1. Kiến Trúc và Xây Dựng

Trong kiến trúc, các kiến trúc sư thường xuyên sử dụng hình chóp để thiết kế mái nhà, tháp, và các công trình độc đáo khác. Việc tính toán thể tích giúp xác định lượng vật liệu cần thiết, đảm bảo tính thẩm mỹ và độ bền của công trình.

3.2. Thiết Kế và Sản Xuất

Trong thiết kế sản phẩm, hình chóp được sử dụng để tạo ra các mẫu mã độc đáo, từ đồ trang trí đến các bộ phận máy móc. Việc tính toán thể tích giúp tối ưu hóa việc sử dụng vật liệu và đảm bảo tính chức năng của sản phẩm.

3.3. Địa Chất và Khoáng Sản

Trong địa chất học, các nhà khoa học sử dụng hình chóp để mô hình hóa các cấu trúc địa chất, như núi lửa và các mỏ khoáng sản. Việc tính toán thể tích giúp ước lượng trữ lượng tài nguyên và dự đoán các hiện tượng tự nhiên.

4. Mẹo Giải Nhanh Bài Tập Thể Tích Hình Chóp

Để giải nhanh các bài tập về thể tích hình chóp, bạn có thể áp dụng một số mẹo sau:

• Xác định rõ loại hình chóp: Nắm vững đặc điểm của từng loại hình chóp (tam giác, tứ giác, lục giác,…) để áp dụng công thức phù hợp.
• Tìm mối liên hệ giữa các yếu tố: Phân tích đề bài để tìm ra mối liên hệ giữa diện tích đáy, chiều cao và các yếu tố khác.
• Sử dụng các định lý và tính chất: Áp dụng các định lý hình học (Pythagore, Talet,…) và các tính chất đặc biệt của hình chóp để đơn giản hóa bài toán.
• Luyện tập thường xuyên: Thực hành giải nhiều bài tập khác nhau để làm quen với các dạng toán và rèn luyện kỹ năng giải nhanh.

5. Các Bài Tập Thể Tích Hình Chóp Nâng Cao

Để nâng cao kỹ năng giải toán, bạn có thể thử sức với các bài tập thể tích hình chóp nâng cao, đòi hỏi sự tư duy sáng tạo và khả năng vận dụng linh hoạt các công thức.

5.1. Bài Tập Về Tỉ Lệ Thể Tích

Cho hình chóp S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’ sao cho SA’ = (1/2)SA, SB’ = (2/3)SB, SC’ = (3/4)SC. Tính tỉ số thể tích của hai khối chóp S.A’B’C’ và S.ABC.

5.2. Bài Tập Về Hình Chóp Cụt

Cho hình chóp cụt đều ABCD.A’B’C’D’ có cạnh đáy lớn AB = a, cạnh đáy nhỏ A’B’ = b, chiều cao h. Tính thể tích của khối chóp cụt.

5.3. Bài Tập Về Góc và Khoảng Cách

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = a√2. Tính thể tích của hình chóp và khoảng cách từ A đến mặt phẳng (SBC).

6. Tài Liệu Tham Khảo và Nguồn Học Tập Bổ Sung

Để học tốt về thể tích hình chóp, bạn có thể tham khảo các tài liệu và nguồn học tập sau:

• Sách giáo khoa và sách bài tập Toán Hình học lớp 12: Nắm vững kiến thức cơ bản và các dạng bài tập thường gặp.
• Các trang web học toán trực tuyến: Tìm kiếm các bài giảng, bài tập và tài liệu ôn tập về thể tích hình chóp.
• Các diễn đàn và nhóm học tập toán: Tham gia thảo luận, trao đổi kiến thức và kinh nghiệm với các bạn học khác.
• tic.edu.vn: Khám phá nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả.

7. FAQ – Các Câu Hỏi Thường Gặp Về Thể Tích Hình Chóp

Câu hỏi 1: Công thức tính thể tích hình chóp cụt là gì?

Trả lời: V = (1/3) h (S1 + S2 + √(S1 * S2)), trong đó h là chiều cao, S1 và S2 là diện tích hai đáy.

Câu hỏi 2: Làm thế nào để xác định chiều cao của hình chóp?

Trả lời: Chiều cao là khoảng cách từ đỉnh chóp đến mặt đáy, thường là đoạn vuông góc kẻ từ đỉnh xuống đáy.

Câu hỏi 3: Công thức tính diện tích đáy của hình chóp tam giác đều là gì?

Trả lời: S = (a²√3) / 4, trong đó a là độ dài cạnh đáy.

Câu hỏi 4: Hình chóp tứ giác đều có đặc điểm gì?

Trả lời: Đáy là hình vuông, các cạnh bên bằng nhau và các mặt bên là tam giác cân.

Câu hỏi 5: Thể tích hình chóp có âm không?

Trả lời: Không, thể tích luôn là một giá trị dương.

Câu hỏi 6: Ứng dụng của thể tích hình chóp trong thực tế là gì?

Trả lời: Trong kiến trúc, xây dựng, thiết kế sản phẩm, địa chất học, v.v.

Câu hỏi 7: Làm thế nào để giải nhanh các bài tập về thể tích hình chóp?

Trả lời: Xác định loại hình chóp, tìm mối liên hệ giữa các yếu tố, sử dụng định lý và luyện tập thường xuyên.

Câu hỏi 8: Nguồn tài liệu học tập về thể tích hình chóp ở đâu?

Trả lời: Sách giáo khoa, trang web học toán trực tuyến, diễn đàn học tập và tic.edu.vn.

Câu hỏi 9: Làm thế nào để tính thể tích hình chóp khi biết tọa độ các đỉnh?

Trả lời: Sử dụng công thức tính thể tích dựa trên tích có hướng và tích hỗn tạp của các vectơ.

Câu hỏi 10: Tại sao cần học về thể tích hình chóp?

Trả lời: Vì nó là một phần quan trọng của chương trình hình học, có nhiều ứng dụng thực tế và giúp phát triển tư duy không gian.

8. Khám Phá Kho Tài Liệu Và Công Cụ Học Tập Tại tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn mong muốn có các công cụ hỗ trợ học tập hiệu quả và một cộng đồng học tập sôi nổi?

tic.edu.vn chính là giải pháp dành cho bạn. Chúng tôi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cập nhật thông tin giáo dục mới nhất và chính xác, cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả và xây dựng cộng đồng học tập trực tuyến sôi nổi để bạn có thể tương tác và học hỏi lẫn nhau.

Đừng bỏ lỡ cơ hội khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả tại tic.edu.vn ngay hôm nay!

• Email: tic.edu@gmail.com
• Trang web: tic.edu.vn

Với những kiến thức và công cụ mà tic.edu.vn cung cấp, bạn sẽ tự tin chinh phục mọi bài toán về công thức thể tích hình chóp và đạt được thành công trong học tập.