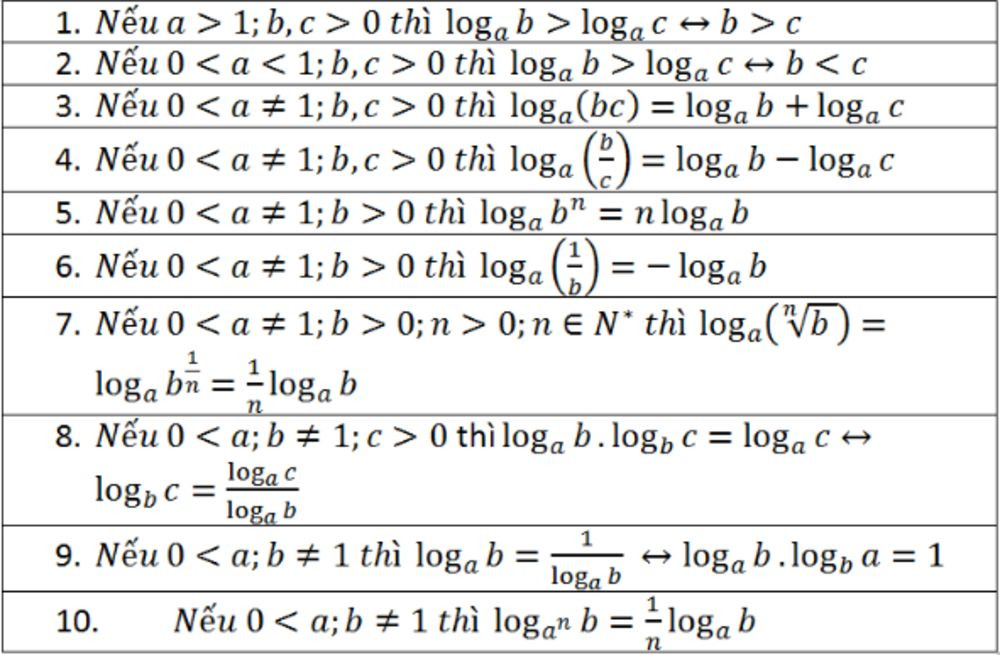
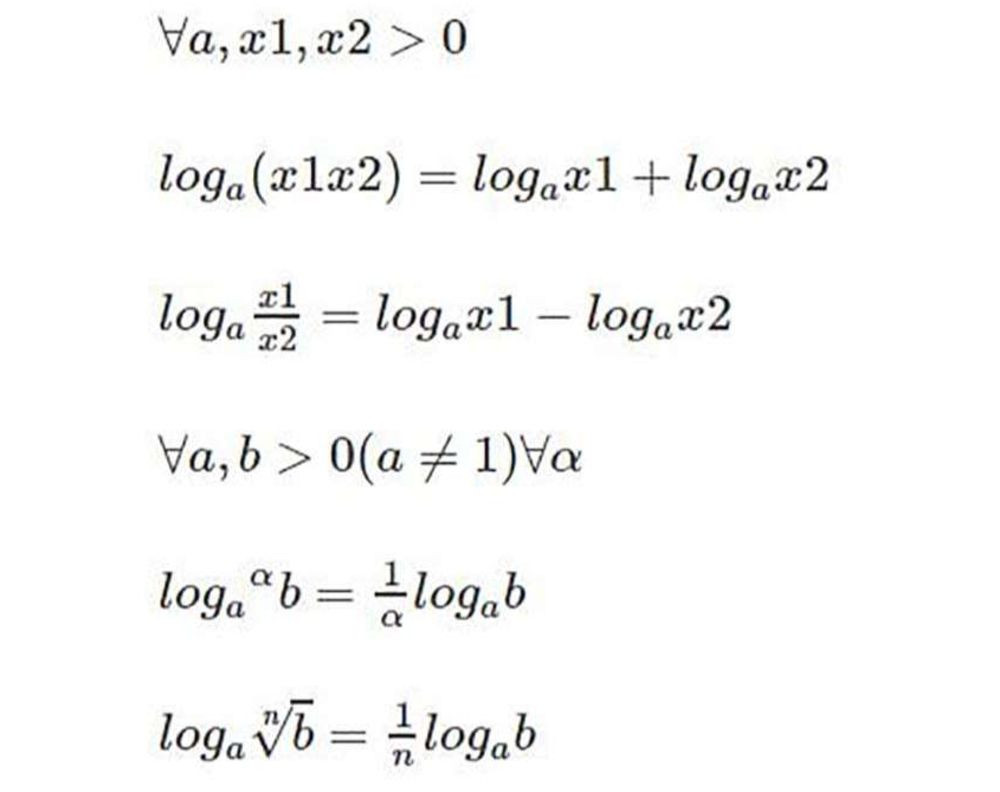
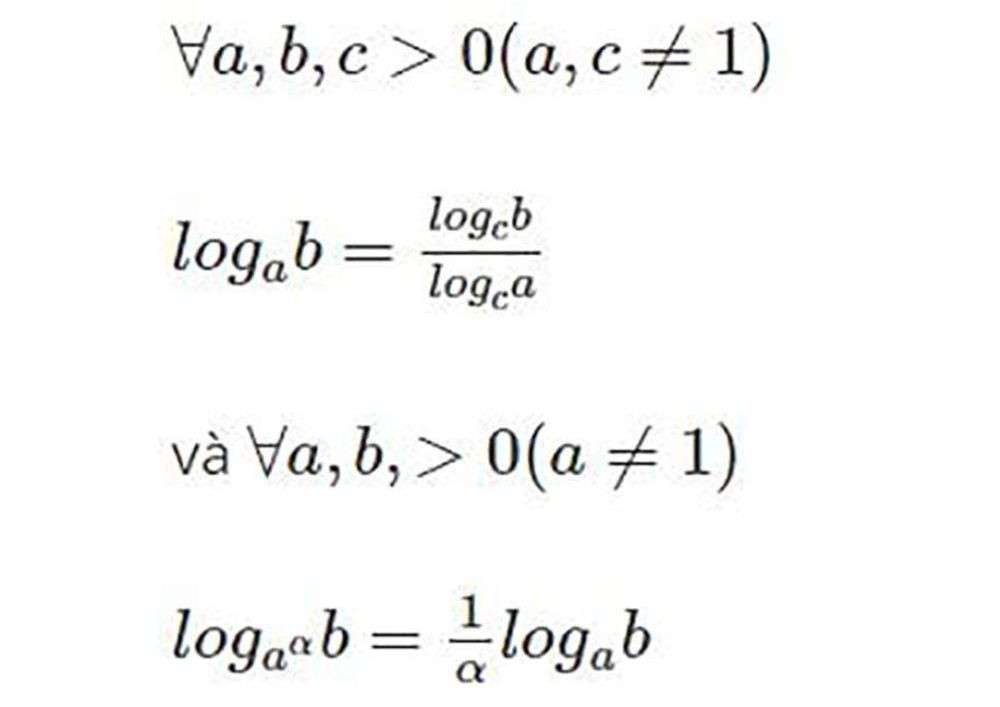
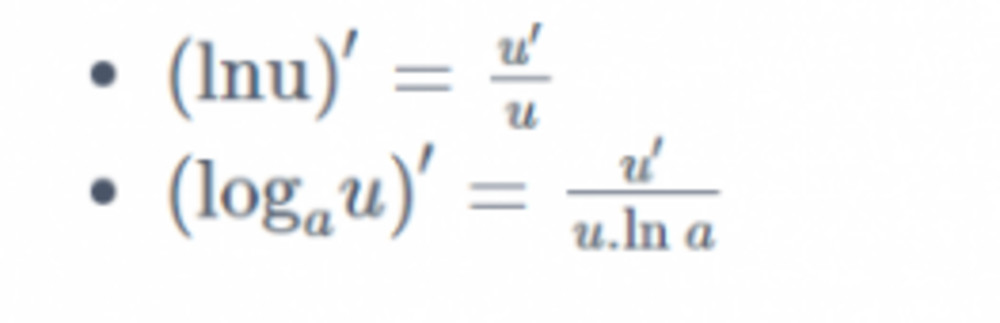
**Công Thức Logarit: Bí Quyết Chinh Phục Toán Học, Ứng Dụng Thực Tế**

Công Thức Logarit là chìa khóa mở cánh cửa thế giới toán học và ứng dụng thực tiễn, giúp bạn giải quyết các bài toán phức tạp một cách dễ dàng. Hãy cùng tic.edu.vn khám phá bí mật của logarit và làm chủ công cụ mạnh mẽ này.

1. Logarit Là Gì? Khám Phá Bản Chất Của Logarit

Logarit là phép toán nghịch đảo của lũy thừa, giúp tìm số mũ cần thiết để đạt được một giá trị cụ thể. Nói một cách đơn giản, logarit trả lời cho câu hỏi: “Cơ số a phải được nâng lên lũy thừa bao nhiêu để được b?”.

Ví dụ: log₂8 = 3 vì 2³ = 8.

1.1. Định Nghĩa Logarit

Cho hai số dương a và b, với a ≠ 1. Logarit cơ số a của b, ký hiệu là logₐb, là số mũ mà a phải được nâng lên để bằng b.

Công thức:

logₐb = x ⇔ aˣ = b

Trong đó:

• a là cơ số (a > 0, a ≠ 1)
• b là số bị logarit (b > 0)
• x là logarit cơ số a của b

1.2. Ví Dụ Minh Họa

• log₁₀100 = 2 vì 10² = 100
• log₃9 = 2 vì 3² = 9
• log₂16 = 4 vì 2⁴ = 16
• log₅125 = 3 vì 5³ = 125
• log₄64 = 3 vì 4³ = 64

1.3. Ứng Dụng Thực Tế Của Logarit

Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, logarit không chỉ là một khái niệm toán học trừu tượng mà còn có vô số ứng dụng thực tế trong nhiều lĩnh vực khác nhau:

• Khoa học: Tính độ pH trong hóa học, đo độ lớn của động đất (thang Richter) trong địa chất học.
• Kỹ thuật: Xử lý tín hiệu, thiết kế mạch điện, phân tích dữ liệu.
• Tài chính: Tính lãi kép, phân tích tăng trưởng đầu tư.
• Âm nhạc: Xác định các khoảng âm nhạc, điều chỉnh âm thanh.
• Tin học: Phân tích độ phức tạp của thuật toán, lưu trữ và xử lý dữ liệu.

Alt: Bảng tính chất logarit với cơ số và đối số dương

2. Các Công Thức Logarit Quan Trọng: Nắm Vững Để Giải Toán

Việc nắm vững các công thức logarit là yếu tố then chốt để giải quyết các bài toán liên quan. Dưới đây là tổng hợp đầy đủ và chi tiết các công thức logarit cần thiết:

2.1. Công Thức Logarit Cơ Bản

• logₐ1 = 0 (Logarit của 1 luôn bằng 0)
• logₐa = 1 (Logarit của cơ số bằng chính nó luôn bằng 1)
• a^(logₐb) = b (Công thức cơ bản về mối liên hệ giữa logarit và lũy thừa)
• logₐ(a^b) = b (Công thức cơ bản về mối liên hệ giữa logarit và lũy thừa)

2.2. Công Thức Logarit Của Một Tích

Logarit của một tích bằng tổng các logarit của từng thừa số.

logₐ(xy) = logₐx + logₐy

Ví dụ: log₂(8*4) = log₂8 + log₂4 = 3 + 2 = 5

2.3. Công Thức Logarit Của Một Thương

Logarit của một thương bằng hiệu các logarit của số bị chia và số chia.

logₐ(x/y) = logₐx – logₐy

Ví dụ: log₅(25/5) = log₅25 – log₅5 = 2 – 1 = 1

2.4. Công Thức Logarit Của Một Lũy Thừa

Logarit của một lũy thừa bằng tích của số mũ và logarit của cơ số.

logₐ(xⁿ) = n*logₐx

Ví dụ: log₂(4³) = 3log₂4 = 32 = 6

2.5. Công Thức Đổi Cơ Số Logarit

Công thức đổi cơ số cho phép chuyển đổi logarit từ cơ số này sang cơ số khác.

logₐb = (logₓb) / (logₓa)

Trong đó x là một cơ số mới tùy ý (x > 0, x ≠ 1).

Hệ quả:

• logₐb = 1 / (logьa)
• logₐb * logьc = logₐc

Ví dụ: log₂8 = (log₁₀8) / (log₁₀2) ≈ 0.903 / 0.301 ≈ 3

2.6. Các Công Thức Logarit Đặc Biệt

• Logarit thập phân: Là logarit cơ số 10, ký hiệu là log₁₀x hoặc lgx.
• Logarit tự nhiên (hay logarit Nepe): Là logarit cơ số e (e ≈ 2.71828), ký hiệu là logₑx hoặc lnx.

Alt: Bảng công thức logarit đầy đủ và chi tiết

3. Bảng Tổng Hợp Công Thức Logarit: Tra Cứu Nhanh Chóng, Tiện Lợi

Để giúp bạn dễ dàng tra cứu và áp dụng các công thức logarit, tic.edu.vn xin cung cấp bảng tổng hợp đầy đủ và chi tiết nhất:

Công Thức	Điều Kiện	Ví Dụ
logₐ1 = 0	a > 0, a ≠ 1	log₂1 = 0
logₐa = 1	a > 0, a ≠ 1	log₅5 = 1
a^(logₐb) = b	a > 0, a ≠ 1, b > 0	2^(log₂8) = 8
logₐ(a^b) = b	a > 0, a ≠ 1	log₂(2³) = 3
logₐ(xy) = logₐx + logₐy	a > 0, a ≠ 1, x > 0, y > 0	log₂(4*2) = log₂4 + log₂2 = 2 + 1 = 3
logₐ(x/y) = logₐx – logₐy	a > 0, a ≠ 1, x > 0, y > 0	log₅(25/5) = log₅25 – log₅5 = 2 – 1 = 1
logₐ(xⁿ) = n*logₐx	a > 0, a ≠ 1, x > 0	log₂(4³) = 3log₂4 = 32 = 6
logₐb = (logₓb) / (logₓa)	a > 0, a ≠ 1, b > 0, x > 0, x ≠ 1	log₂8 = (log₁₀8) / (log₁₀2) ≈ 3
logₐb = 1 / (logьa)	a > 0, a ≠ 1, b > 0, b ≠ 1	log₂8 = 1 / (log₈2)
logₐb * logьc = logₐc	a > 0, a ≠ 1, b > 0, b ≠ 1, c > 0	log₂4 * log₄16 = log₂16 = 4

4. Công Thức Lũy Thừa Logarit: Mở Rộng Khả Năng Giải Toán

Công thức lũy thừa logarit là một công cụ hữu ích để đơn giản hóa và giải quyết các bài toán phức tạp liên quan đến lũy thừa và logarit.

4.1. Công Thức Cơ Bản

a^(logₐb) = b

Công thức này cho thấy mối quan hệ nghịch đảo giữa lũy thừa và logarit. Nếu bạn nâng cơ số a lên lũy thừa là logarit cơ số a của b, kết quả sẽ là b.

Ví dụ: 5^(log₅25) = 25

4.2. Các Biến Thể Của Công Thức

• e^(lnx) = x (Với e là cơ số của logarit tự nhiên và lnx là logarit tự nhiên của x)
• 10^(logx) = x (Với logx là logarit thập phân của x)

4.3. Ứng Dụng Của Công Thức Lũy Thừa Logarit

• Giải phương trình: Công thức lũy thừa logarit được sử dụng để giải các phương trình mũ và logarit phức tạp.
• Đơn giản hóa biểu thức: Giúp đơn giản hóa các biểu thức chứa cả lũy thừa và logarit.
• Chứng minh đẳng thức: Được sử dụng để chứng minh các đẳng thức liên quan đến lũy thừa và logarit.

Alt: Bảng công thức lũy thừa logarit đầy đủ

5. Công Thức Logarit Với Các Phép Toán: Cộng, Trừ, Nhân, Chia

Logarit có mối liên hệ chặt chẽ với các phép toán cơ bản, giúp chúng ta đơn giản hóa các biểu thức phức tạp.

5.1. Logarit Của Một Tích

logₐ(xy) = logₐx + logₐy

Ví dụ: log₂(4*8) = log₂4 + log₂8 = 2 + 3 = 5

5.2. Logarit Của Một Thương

logₐ(x/y) = logₐx – logₐy

Ví dụ: log₅(125/5) = log₅125 – log₅5 = 3 – 1 = 2

5.3. Lưu Ý

Không có công thức logarit cho tổng hoặc hiệu của hai số. Tức là, logₐ(x + y) ≠ logₐx + logₐy và logₐ(x – y) ≠ logₐx – logₐy.

Alt: Bảng công thức logarit với các phép toán cộng, trừ, nhân, chia

6. Công Thức Phép Đổi Cơ Số: Chuyển Đổi Linh Hoạt Giữa Các Cơ Số

Công thức đổi cơ số là một công cụ mạnh mẽ cho phép chuyển đổi logarit từ cơ số này sang cơ số khác một cách dễ dàng.

6.1. Công Thức Tổng Quát

logₐb = (logₓb) / (logₓa)

Trong đó:

• a là cơ số ban đầu
• b là số bị logarit
• x là cơ số mới (x > 0, x ≠ 1)

6.2. Hệ Quả Quan Trọng

• logₐb = 1 / (logьa) (Đảo ngược cơ số và số bị logarit)
• logₐb * logьc = logₐc (Quy tắc chuỗi)

6.3. Ứng Dụng Của Công Thức Đổi Cơ Số

• Tính toán logarit với cơ số không quen thuộc: Chuyển đổi về cơ số 10 hoặc cơ số e để sử dụng máy tính.
• Đơn giản hóa biểu thức: Giúp đơn giản hóa các biểu thức chứa logarit với nhiều cơ số khác nhau.
• Giải phương trình: Được sử dụng để giải các phương trình logarit phức tạp.

Alt: Bảng công thức phép đổi cơ số logarit

7. Công Thức Đạo Hàm Logarit: Chinh Phục Giải Tích

Đạo hàm logarit là một công cụ quan trọng trong giải tích, giúp tìm đạo hàm của các hàm số phức tạp chứa logarit.

7.1. Đạo Hàm Logarit Hàm Cơ Bản

• (lnx)’ = 1/x (Đạo hàm của logarit tự nhiên của x)
• (logₐx)’ = 1/(x*lna) (Đạo hàm của logarit cơ số a của x)

7.2. Đạo Hàm Logarit Hàm Hợp

Nếu u(x) là một hàm số của x, thì:

• (ln(u(x)))’ = u'(x) / u(x)
• (logₐ(u(x)))’ = u'(x) / (u(x)*lna)

7.3. Ứng Dụng Của Đạo Hàm Logarit

• Tìm cực trị của hàm số: Đạo hàm logarit giúp tìm các điểm cực trị của các hàm số chứa logarit.
• Khảo sát hàm số: Được sử dụng để khảo sát sự biến thiên và vẽ đồ thị của hàm số.
• Giải phương trình vi phân: Đạo hàm logarit xuất hiện trong nhiều bài toán liên quan đến phương trình vi phân.

Alt: Bảng công thức đạo hàm logarit hàm cơ bản và hàm hợp

8. Quy Tắc Tính Logarit: Nắm Vững Để Giải Nhanh Bài Tập

Để giải quyết các bài toán logarit một cách nhanh chóng và chính xác, bạn cần nắm vững các quy tắc sau:

8.1. Quy Tắc Logarit Của Lũy Thừa

logₐ(b^α) = α*logₐb

Ví dụ: log₂(8²) = 2log₂8 = 23 = 6

8.2. Quy Tắc Logarit Của Một Tích

logₐ(bc) = logₐb + logₐc

Ví dụ: log₂(4*8) = log₂4 + log₂8 = 2 + 3 = 5

8.3. Quy Tắc Sử Dụng Bảng Logarit

• Đưa về cơ số 10: Chuyển đổi logarit về cơ số 10 (logarit thập phân) để sử dụng bảng logarit.
• Tra bảng và tính toán: Sử dụng bảng logarit để tìm giá trị logarit của các số, sau đó thực hiện các phép tính cần thiết.

9. Cách Tìm Logarit: Hướng Dẫn Chi Tiết Từ Cơ Bản Đến Nâng Cao

Việc tìm logarit có thể thực hiện bằng nhiều cách khác nhau, tùy thuộc vào độ phức tạp của bài toán.

9.1. Tìm Logarit Nhanh

• Tìm giá trị ô đúng: Xác định giao điểm của hàng và cột tương ứng trong bảng logarit.
• Chọn đúng bảng: Sử dụng bảng logarit thập phân (cơ số 10) hoặc bảng logarit tự nhiên (cơ số e) tùy theo yêu cầu của bài toán.
• Tìm phần nguyên: Đếm số chữ số của số bị logarit, trừ đi 1 để tìm phần nguyên của logarit.
• Tìm phần thập phân: Sử dụng bảng logarit để tìm phần thập phân (mantissa) của logarit.

9.2. Tìm Logarit Nâng Cao

• Hiểu rõ định nghĩa logarit: Nắm vững khái niệm logarit và mối quan hệ với lũy thừa.
• Xác định đặc tính của số: Phân tích số bị logarit để áp dụng các công thức và quy tắc phù hợp.
• Sử dụng bảng logarit cẩn thận: Tra cứu bảng logarit một cách chính xác, chú ý đến hàng và cột tương ứng.
• Thêm đặc tính với mantissa: Kết hợp phần nguyên (đặc tính) và phần thập phân (mantissa) để có kết quả logarit cuối cùng.

10. Lưu Ý Khi Học Công Thức Logarit: Bí Quyết Ghi Nhớ Lâu Dài

Để học và ghi nhớ công thức logarit một cách hiệu quả, bạn cần lưu ý những điều sau:

• Phân biệt hàm mũ và logarit: Hiểu rõ sự khác biệt giữa phương trình mũ và phương trình logarit.
• Ghi nhớ thành phần của công thức: Nhận biết các thành phần cơ bản của công thức logarit (cơ số, số bị logarit, logarit).
• Phân biệt các loại logarit: Nắm vững sự khác nhau giữa logarit thập phân, logarit tự nhiên, logarit nhị phân, v.v.
• Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các công thức và quy tắc logarit.
• Trao đổi và tham khảo ý kiến: Thảo luận với bạn bè, thầy cô giáo để hiểu sâu hơn về logarit.
• Tham khảo tài liệu uy tín: Tìm kiếm thông tin trên các website, diễn đàn, sách giáo khoa uy tín.

Alt: Những lưu ý quan trọng khi học công thức logarit

11. Bài Tập Vận Dụng Công Thức Logarit: Rèn Luyện Kỹ Năng Giải Toán

Để củng cố kiến thức và rèn luyện kỹ năng giải toán logarit, hãy cùng tic.edu.vn giải các bài tập sau:

11.1. Dạng 1: So Sánh Các Biểu Thức Chứa Logarit

Bài tập: So sánh các biểu thức sau:

• A = ln5
• B = ln3 + ln2

Hướng dẫn giải:

1. Sử dụng tính chất logarit: B = ln(3*2) = ln6
2. So sánh: Vì 5 < 6 nên ln5 < ln6, suy ra A < B.

11.2. Dạng 2: Biểu Diễn Logarit Qua Các Logarit Đã Cho

Bài tập: Cho log₂3 = a, log₂5 = b. Hãy biểu diễn log₂45 theo a và b.

Hướng dẫn giải:

1. Phân tích: 45 = 3² * 5
2. Sử dụng tính chất logarit: log₂45 = log₂(3² 5) = log₂(3²) + log₂5 = 2log₂3 + log₂5 = 2a + b

11.3. Dạng 3: Rút Gọn Biểu Thức Logarit

Bài tập: Rút gọn biểu thức: A = log₃(9x) – log₃x

Hướng dẫn giải:

1. Sử dụng tính chất logarit: A = log₃9 + log₃x – log₃x = log₃9 = 2

12. FAQ: Giải Đáp Thắc Mắc Về Công Thức Logarit

Dưới đây là một số câu hỏi thường gặp về công thức logarit và giải đáp chi tiết từ tic.edu.vn:

1. Logarit dùng để làm gì?
   • Logarit được sử dụng để giải các bài toán liên quan đến lũy thừa, đo độ lớn của động đất, tính độ pH, v.v.
2. Có mấy loại logarit?
   • Có nhiều loại logarit khác nhau, phổ biến nhất là logarit thập phân (cơ số 10) và logarit tự nhiên (cơ số e).
3. Làm sao để nhớ công thức logarit?
   • Bạn nên hiểu rõ bản chất của logarit, luyện tập thường xuyên và sử dụng bảng tổng hợp công thức để tra cứu khi cần thiết.
4. Công thức đổi cơ số logarit dùng để làm gì?
   • Công thức đổi cơ số giúp chuyển đổi logarit từ cơ số này sang cơ số khác, giúp tính toán và đơn giản hóa biểu thức.
5. Đạo hàm logarit được ứng dụng như thế nào?
   • Đạo hàm logarit được sử dụng để tìm cực trị của hàm số, khảo sát hàm số và giải phương trình vi phân.
6. Có thể tìm tài liệu học tập về logarit ở đâu?
   • Bạn có thể tìm tài liệu học tập về logarit trên tic.edu.vn, sách giáo khoa, website giáo dục uy tín, v.v.
7. tic.edu.vn có những công cụ hỗ trợ học tập nào về logarit?
   • tic.edu.vn cung cấp các bài viết tổng hợp công thức, bài tập vận dụng, công cụ tính toán logarit trực tuyến và cộng đồng hỗ trợ học tập.
8. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?
   • Bạn có thể truy cập tic.edu.vn, đăng ký tài khoản và tham gia vào các diễn đàn, nhóm học tập để trao đổi kiến thức và kinh nghiệm.
9. tic.edu.vn có những khóa học nào về logarit?
   • tic.edu.vn liên tục cập nhật các khóa học về logarit từ cơ bản đến nâng cao, phù hợp với nhiều đối tượng học viên.
10. Tôi có thể liên hệ với tic.edu.vn để được tư vấn về logarit như thế nào?
    • Bạn có thể liên hệ với tic.edu.vn qua email: [email protected] hoặc truy cập website: tic.edu.vn để được hỗ trợ.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kiến thức và kỹ năng giải toán logarit? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu phong phú, công cụ hỗ trợ hiệu quả và cộng đồng học tập sôi nổi. Đừng bỏ lỡ cơ hội chinh phục toán học và mở rộng cánh cửa tri thức! Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập website: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.