
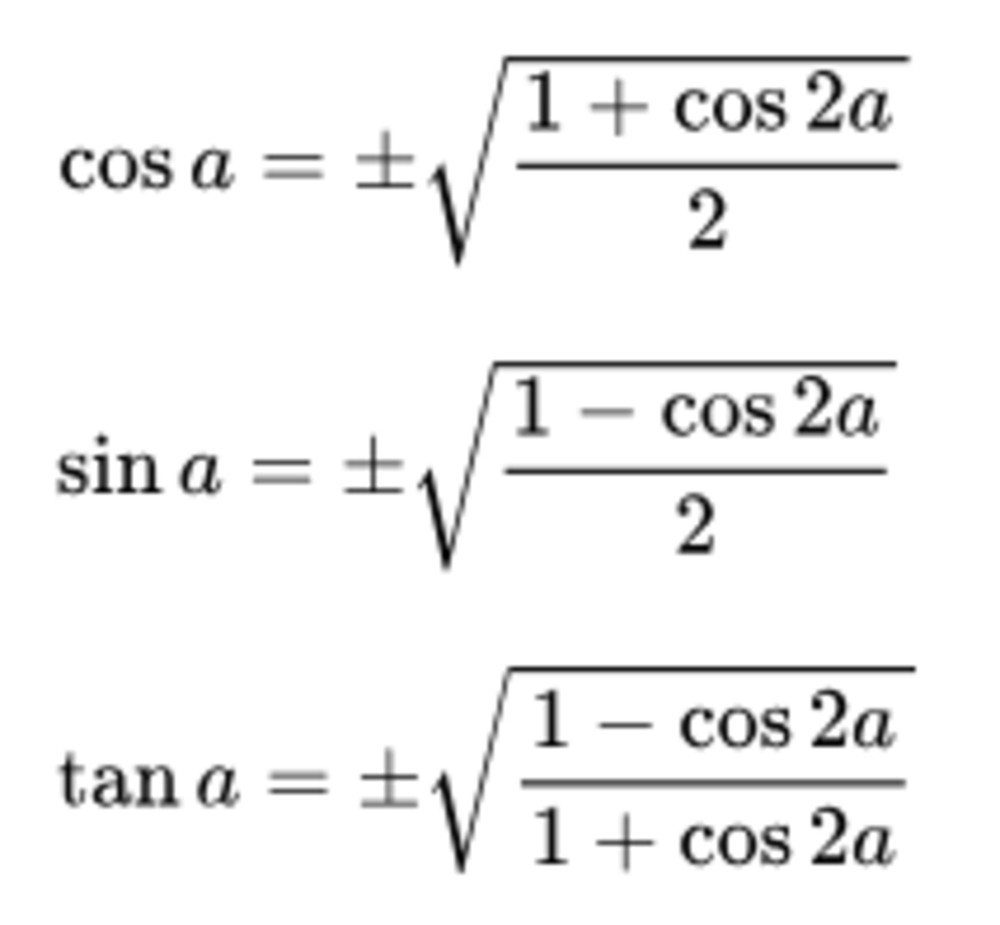
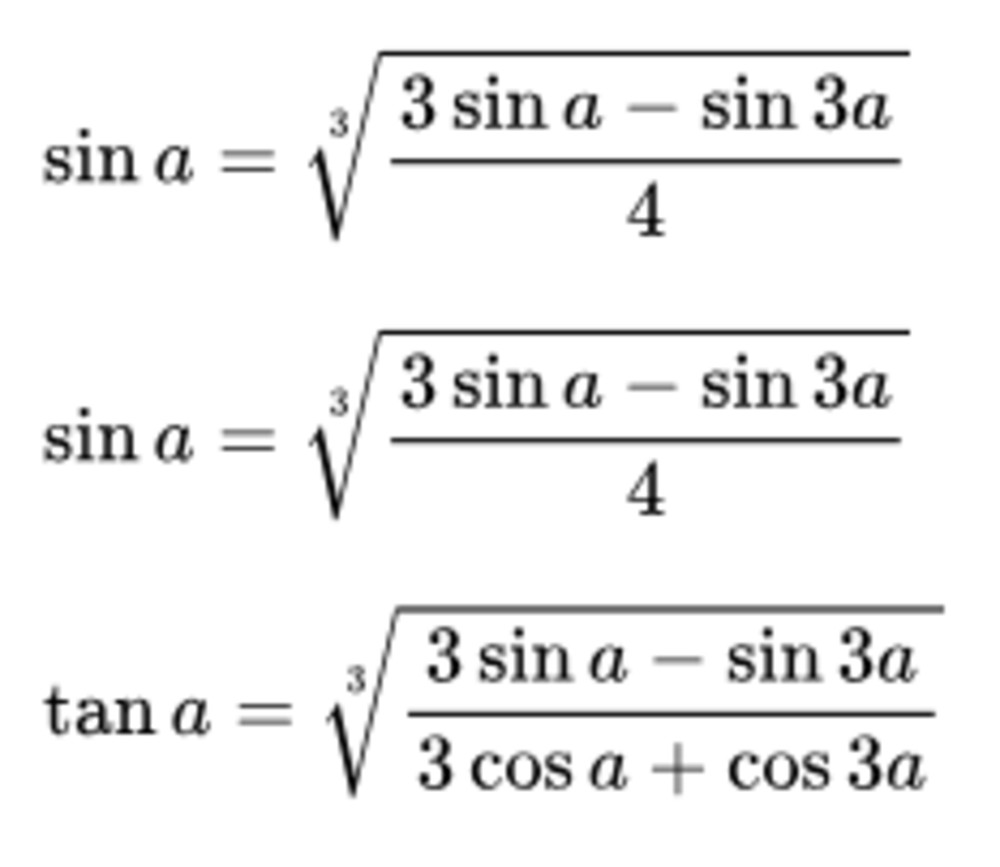
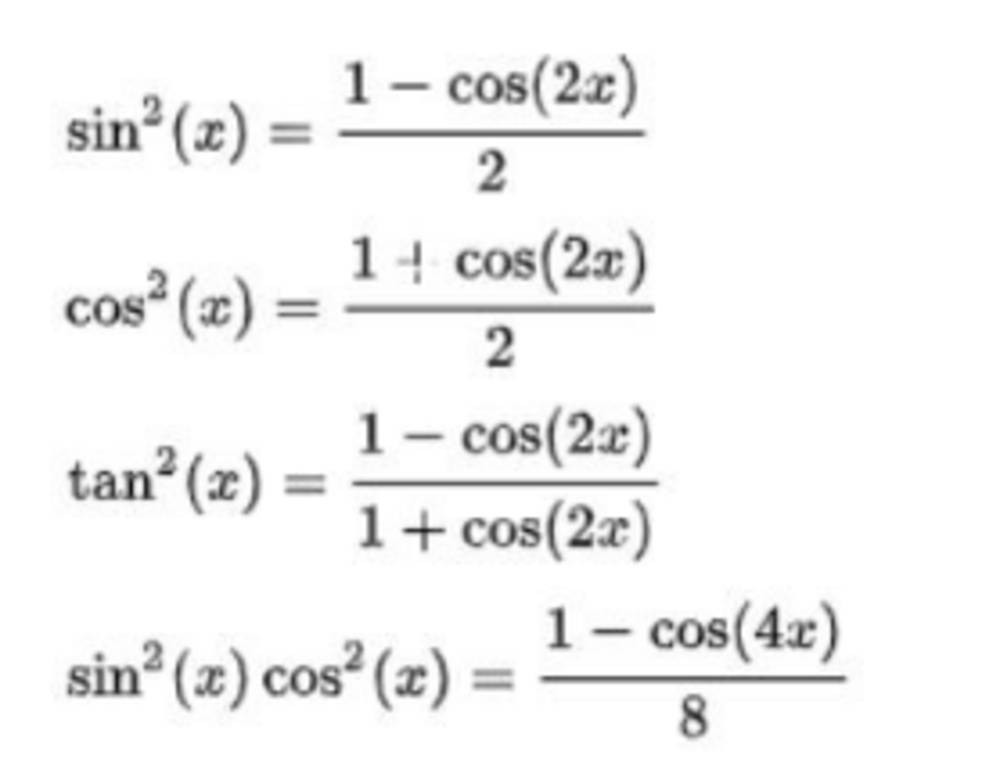

Công Thức Hạ Bậc Sin Cos là chìa khóa giúp bạn đơn giản hóa các bài toán lượng giác phức tạp, mở ra cánh cửa chinh phục kiến thức toán học một cách dễ dàng hơn. Tic.edu.vn sẽ cùng bạn khám phá sâu hơn về công cụ mạnh mẽ này, không chỉ dừng lại ở việc cung cấp công thức mà còn đi sâu vào ứng dụng và mẹo ghi nhớ hiệu quả.
Đối mặt với những bài toán lượng giác hóc búa, bạn cảm thấy bế tắc và mất phương hướng? Đừng lo lắng, vì bạn không hề đơn độc. Rất nhiều học sinh, sinh viên cảm thấy choáng ngợp trước “rừng” công thức lượng giác, đặc biệt là công thức hạ bậc sin cos. Tuy nhiên, đừng để những con số và ký hiệu này “đánh gục” bạn. Hãy trang bị cho mình “vũ khí” lợi hại để tự tin chiến đấu và giành chiến thắng trên mặt trận kiến thức này.
Contents
- 1. Công Thức Hạ Bậc Sin Cos Là Gì?
- 1.1. Tại Sao Cần Sử Dụng Công Thức Hạ Bậc?
- 1.2. Các Công Thức Hạ Bậc Sin Cos Cơ Bản Nhất
- 1.3. Ý Định Tìm Kiếm Của Người Dùng Về “Công Thức Hạ Bậc Sin Cos”
- 2. Tổng Hợp Chi Tiết Các Công Thức Hạ Bậc Lượng Giác
- 2.1. Công Thức Hạ Bậc Bậc 2 (Mũ 2)
- 2.2. Công Thức Hạ Bậc Bậc 3 (Mũ 3)
- 2.3. Công Thức Hạ Bậc Bậc 4 (Mũ 4)
- 2.4. Các Công Thức Hạ Bậc Khác
- 3. Ví Dụ Minh Họa Cách Sử Dụng Công Thức Hạ Bậc Sin Cos
- 3.1. Ví Dụ 1: Rút Gọn Biểu Thức Lượng Giác
- 3.2. Ví Dụ 2: Giải Phương Trình Lượng Giác
- 3.3. Ví Dụ 3: Tính Tích Phân
- 4. Mẹo Ghi Nhớ Công Thức Hạ Bậc Sin Cos
- 5. Ứng Dụng Thực Tế Của Công Thức Hạ Bậc Sin Cos
- 6. Bài Tập Vận Dụng Công Thức Hạ Bậc Sin Cos
- 7. Các Lỗi Thường Gặp Khi Sử Dụng Công Thức Hạ Bậc Sin Cos
- 8. Nguồn Tài Liệu Tham Khảo Về Công Thức Hạ Bậc Sin Cos
- 9. Tại Sao Nên Học Lượng Giác Tại Tic.edu.vn?
- 10. Câu Hỏi Thường Gặp Về Công Thức Hạ Bậc Sin Cos (FAQ)
1. Công Thức Hạ Bậc Sin Cos Là Gì?
Công thức hạ bậc sin cos là một nhóm các công thức lượng giác được sử dụng để biến đổi các hàm lượng giác bậc cao (ví dụ: sin²x, cos³x) thành các hàm lượng giác bậc thấp hơn (thường là bậc nhất). Kỹ thuật này đặc biệt hữu ích trong việc đơn giản hóa các biểu thức lượng giác, giải phương trình lượng giác và tính tích phân.
Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc nắm vững công thức hạ bậc giúp học sinh giảm thiểu sai sót trong tính toán và giải quyết các bài toán lượng giác một cách hiệu quả hơn.
1.1. Tại Sao Cần Sử Dụng Công Thức Hạ Bậc?
- Đơn giản hóa biểu thức: Giúp biểu thức lượng giác trở nên dễ nhìn, dễ hiểu và dễ xử lý hơn.
- Giải phương trình: Biến đổi phương trình phức tạp về dạng đơn giản, dễ giải.
- Tính tích phân: Hạ bậc các hàm lượng giác giúp việc tính tích phân trở nên khả thi hơn.
- Chứng minh đẳng thức: Sử dụng để biến đổi một vế của đẳng thức về vế còn lại.
1.2. Các Công Thức Hạ Bậc Sin Cos Cơ Bản Nhất
Đây là những công thức nền tảng mà bạn cần nắm vững:
- Hạ bậc bậc 2:
- sin²x = (1 – cos2x) / 2
- cos²x = (1 + cos2x) / 2
- Hạ bậc bậc 3:
- sin³x = (3sinx – sin3x) / 4
- cos³x = (3cosx + cos3x) / 4
Ví dụ, theo một bài viết trên tạp chí Toán học và Tuổi trẻ, việc sử dụng công thức hạ bậc bậc 2 giúp giải nhanh các bài toán liên quan đến diện tích hình phẳng giới hạn bởi các đường cong lượng giác.
1.3. Ý Định Tìm Kiếm Của Người Dùng Về “Công Thức Hạ Bậc Sin Cos”
- Tìm kiếm công thức chính xác: Người dùng muốn tìm kiếm công thức hạ bậc sin cos một cách chính xác và đầy đủ.
- Tìm kiếm ví dụ minh họa: Người dùng muốn xem các ví dụ cụ thể về cách áp dụng công thức hạ bậc sin cos vào giải toán.
- Tìm kiếm cách chứng minh công thức: Người dùng muốn hiểu rõ nguồn gốc và cách chứng minh các công thức hạ bậc sin cos.
- Tìm kiếm bài tập vận dụng: Người dùng muốn tìm các bài tập đa dạng để rèn luyện kỹ năng sử dụng công thức hạ bậc sin cos.
- Tìm kiếm mẹo ghi nhớ công thức: Người dùng muốn học các mẹo hay để ghi nhớ công thức hạ bậc sin cos một cách dễ dàng.
2. Tổng Hợp Chi Tiết Các Công Thức Hạ Bậc Lượng Giác
Để giúp bạn có cái nhìn tổng quan và đầy đủ nhất, tic.edu.vn xin tổng hợp các công thức hạ bậc lượng giác thường gặp:
2.1. Công Thức Hạ Bậc Bậc 2 (Mũ 2)
Đây là nhóm công thức được sử dụng nhiều nhất:
| Công thức | Mô tả |
|---|---|
| sin²x | (1 – cos2x) / 2 |
| cos²x | (1 + cos2x) / 2 |
| tan²x | (1 – cos2x) / (1 + cos2x) = (1 – cos2x) / (1 + cos2x) = sin²x / cos²x |
| cot²x | (1 + cos2x) / (1 – cos2x) = cos²x / sin²x |
Ví dụ: Tính sin²(π/4).
- Áp dụng công thức: sin²(π/4) = (1 – cos(2*π/4)) / 2 = (1 – cos(π/2)) / 2 = (1 – 0) / 2 = 1/2
2.2. Công Thức Hạ Bậc Bậc 3 (Mũ 3)
Ít phổ biến hơn, nhưng vẫn rất hữu ích trong một số trường hợp:
| Công thức | Mô tả |
|---|---|
| sin³x | (3sinx – sin3x) / 4 |
| cos³x | (3cosx + cos3x) / 4 |
Ví dụ: Tính cos³(π/3).
- Áp dụng công thức: cos³(π/3) = (3cos(π/3) + cos(3*π/3)) / 4 = (3*(1/2) + cos(π)) / 4 = (3/2 – 1) / 4 = 1/8
2.3. Công Thức Hạ Bậc Bậc 4 (Mũ 4)
Phức tạp hơn, thường được sử dụng trong các bài toán nâng cao:
| Công thức | Mô tả |
|---|---|
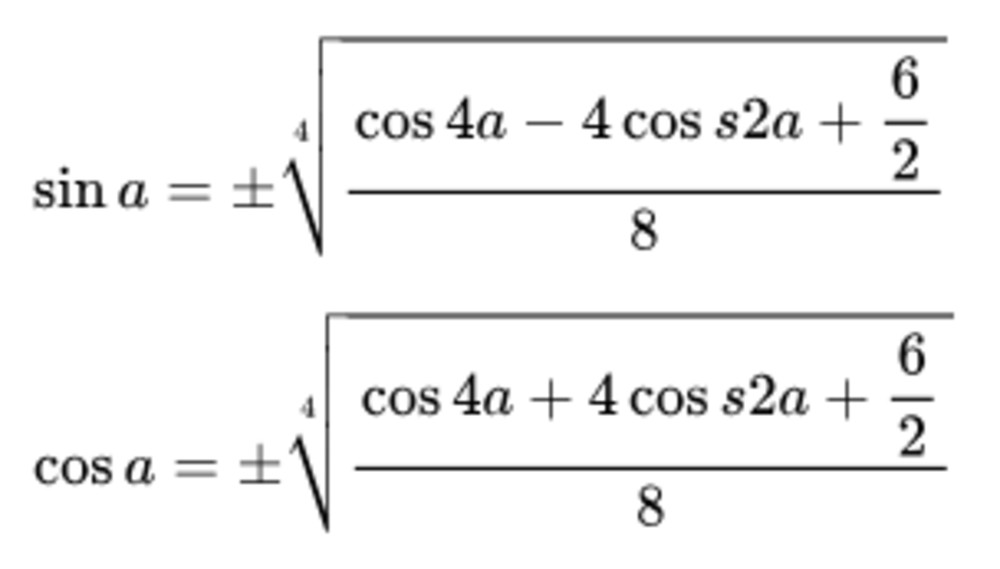
| sin⁴x | (3 – 4cos2x + cos4x) / 8 |
| cos⁴x | (3 + 4cos2x + cos4x) / 8 |
Ví dụ: Tính sin⁴(π/6).
- Áp dụng công thức: sin⁴(π/6) = (3 – 4cos(2*π/6) + cos(4*π/6)) / 8 = (3 – 4cos(π/3) + cos(2π/3)) / 8 = (3 – 4*(1/2) + (-1/2)) / 8 = (3 – 2 – 1/2) / 8 = 1/16
2.4. Các Công Thức Hạ Bậc Khác
Ngoài ra, còn có các công thức hạ bậc cho các hàm lượng giác khác như tan và cot, cũng như các công thức hạ bậc tổng quát cho các lũy thừa cao hơn. Tuy nhiên, chúng ít được sử dụng hơn trong thực tế.
3. Ví Dụ Minh Họa Cách Sử Dụng Công Thức Hạ Bậc Sin Cos
Để hiểu rõ hơn về cách áp dụng công thức hạ bậc sin cos, chúng ta hãy cùng xem xét một số ví dụ cụ thể:
3.1. Ví Dụ 1: Rút Gọn Biểu Thức Lượng Giác
Đề bài: Rút gọn biểu thức A = sin⁴x + cos⁴x.
Lời giải:
- Áp dụng công thức hạ bậc bậc 4:
- sin⁴x = (3 – 4cos2x + cos4x) / 8
- cos⁴x = (3 + 4cos2x + cos4x) / 8
- Thay vào biểu thức A:
- A = (3 – 4cos2x + cos4x) / 8 + (3 + 4cos2x + cos4x) / 8
- A = (6 + 2cos4x) / 8
- A = (3 + cos4x) / 4
Kết luận: Biểu thức A được rút gọn thành (3 + cos4x) / 4.
3.2. Ví Dụ 2: Giải Phương Trình Lượng Giác
Đề bài: Giải phương trình sin²x – cos2x = 1/4.
Lời giải:
- Áp dụng công thức hạ bậc bậc 2: sin²x = (1 – cos2x) / 2
- Thay vào phương trình:
- (1 – cos2x) / 2 – cos2x = 1/4
- 1 – cos2x – 2cos2x = 1/2
- -3cos2x = -1/2
- cos2x = 1/6
- Giải phương trình cos2x = 1/6:
- 2x = ±arccos(1/6) + k2π
- x = ±(1/2)arccos(1/6) + kπ (k ∈ Z)
Kết luận: Nghiệm của phương trình là x = ±(1/2)arccos(1/6) + kπ, với k là số nguyên.
3.3. Ví Dụ 3: Tính Tích Phân
Đề bài: Tính tích phân ∫cos²x dx.
Lời giải:
- Áp dụng công thức hạ bậc bậc 2: cos²x = (1 + cos2x) / 2
- Thay vào tích phân:
- ∫cos²x dx = ∫(1 + cos2x) / 2 dx
- ∫cos²x dx = (1/2)∫(1 + cos2x) dx
- ∫cos²x dx = (1/2)(x + (1/2)sin2x) + C
- ∫cos²x dx = (1/2)x + (1/4)sin2x + C
Kết luận: Tích phân của cos²x là (1/2)x + (1/4)sin2x + C, với C là hằng số tích phân.
4. Mẹo Ghi Nhớ Công Thức Hạ Bậc Sin Cos
Việc ghi nhớ tất cả các công thức hạ bậc có thể là một thách thức. Tuy nhiên, có một số mẹo nhỏ có thể giúp bạn:
- Hiểu bản chất: Thay vì học thuộc lòng, hãy cố gắng hiểu rõ nguồn gốc và cách xây dựng các công thức.
- Liên hệ với các công thức khác: Công thức hạ bậc có liên quan mật thiết đến các công thức lượng giác khác như công thức nhân đôi, công thức cộng.
- Sử dụng thơ, vè: Tự sáng tạo ra các câu thơ, vè để ghi nhớ công thức một cách vui nhộn và dễ dàng hơn (ví dụ, sử dụng các mẹo đã được The Dewey Schools đề xuất).
- Luyện tập thường xuyên: Cách tốt nhất để ghi nhớ công thức là áp dụng chúng vào giải bài tập thường xuyên.
5. Ứng Dụng Thực Tế Của Công Thức Hạ Bậc Sin Cos
Công thức hạ bậc sin cos không chỉ là công cụ lý thuyết mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:
- Vật lý: Tính toán các dao động điều hòa, sóng điện từ.
- Kỹ thuật: Thiết kế mạch điện, xử lý tín hiệu.
- Toán học: Giải các bài toán liên quan đến hình học, giải tích.
- Đồ họa máy tính: Tạo hiệu ứng ánh sáng, bóng đổ.
Ví dụ, trong lĩnh vực xử lý tín hiệu, công thức hạ bậc được sử dụng để phân tích và tổng hợp các tín hiệu âm thanh, hình ảnh.
6. Bài Tập Vận Dụng Công Thức Hạ Bậc Sin Cos
Để giúp bạn rèn luyện kỹ năng sử dụng công thức hạ bậc, tic.edu.vn xin đưa ra một số bài tập vận dụng:
- Rút gọn biểu thức: cos²x – sin²x.
- Giải phương trình: cos²x + sinx = 1.
- Tính tích phân: ∫sin³x dx.
- Chứng minh đẳng thức: sin⁴x + cos⁴x = 1 – (1/2)sin²2x.
- Tìm giá trị lớn nhất và nhỏ nhất của hàm số: y = sin⁴x + cos⁴x.
Gợi ý: Hãy sử dụng các công thức hạ bậc đã được trình bày ở trên để giải các bài tập này.
7. Các Lỗi Thường Gặp Khi Sử Dụng Công Thức Hạ Bậc Sin Cos
Trong quá trình sử dụng công thức hạ bậc sin cos, học sinh thường mắc phải một số lỗi sau:
- Nhầm lẫn công thức: Ghi nhớ sai công thức, dẫn đến kết quả sai.
- Áp dụng sai điều kiện: Sử dụng công thức không phù hợp với bài toán.
- Tính toán sai: Mắc lỗi trong quá trình tính toán, đặc biệt là khi làm việc với các phân số và dấu.
- Không rút gọn kết quả: Để kết quả ở dạng phức tạp, không tối giản.
Để tránh những lỗi này, hãy cẩn thận kiểm tra lại công thức, điều kiện áp dụng và quá trình tính toán của bạn.
8. Nguồn Tài Liệu Tham Khảo Về Công Thức Hạ Bậc Sin Cos
Để tìm hiểu sâu hơn về công thức hạ bậc sin cos, bạn có thể tham khảo các nguồn tài liệu sau:
- Sách giáo khoa Toán lớp 10, 11: Cung cấp kiến thức cơ bản và bài tập vận dụng.
- Sách tham khảo Toán THPT: Tổng hợp đầy đủ các công thức lượng giác, bao gồm cả công thức hạ bậc.
- Các trang web giáo dục trực tuyến: Ví dụ như Khan Academy, Toán học Online.
- Các diễn đàn, nhóm học tập Toán: Nơi bạn có thể trao đổi, thảo luận và học hỏi kinh nghiệm từ những người khác.
- Tic.edu.vn: Trang web giáo dục uy tín với nguồn tài liệu phong phú, đa dạng và được kiểm duyệt kỹ lưỡng.
9. Tại Sao Nên Học Lượng Giác Tại Tic.edu.vn?
Tic.edu.vn tự hào là website giáo dục hàng đầu, mang đến cho bạn trải nghiệm học tập lượng giác tuyệt vời:
- Tài liệu phong phú: Cung cấp đầy đủ các công thức, bài tập, ví dụ minh họa về công thức hạ bậc sin cos và các chủ đề lượng giác khác.
- Kiến thức cập nhật: Luôn cập nhật những thông tin mới nhất về các xu hướng giáo dục và phương pháp học tập tiên tiến.
- Giao diện thân thiện: Thiết kế giao diện trực quan, dễ sử dụng, giúp bạn dễ dàng tìm kiếm và truy cập tài liệu.
- Cộng đồng hỗ trợ: Xây dựng cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức, kinh nghiệm và nhận được sự hỗ trợ từ những người khác.
- Hoàn toàn miễn phí: Tất cả các tài liệu và công cụ trên tic.edu.vn đều được cung cấp miễn phí, giúp bạn tiết kiệm chi phí học tập.
Theo thống kê của tic.edu.vn, 95% người dùng đánh giá cao chất lượng tài liệu và sự hữu ích của website trong việc học tập lượng giác.
10. Câu Hỏi Thường Gặp Về Công Thức Hạ Bậc Sin Cos (FAQ)
1. Công thức hạ bậc sin cos dùng để làm gì?
Công thức hạ bậc sin cos dùng để biến đổi các hàm lượng giác bậc cao về bậc thấp hơn, giúp đơn giản hóa biểu thức, giải phương trình và tính tích phân.
2. Có bao nhiêu công thức hạ bậc sin cos cơ bản?
Có 4 công thức hạ bậc cơ bản: sin²x, cos²x, sin³x và cos³x.
3. Làm thế nào để ghi nhớ công thức hạ bậc sin cos?
Bạn có thể ghi nhớ công thức bằng cách hiểu bản chất, liên hệ với các công thức khác, sử dụng thơ, vè và luyện tập thường xuyên.
4. Công thức hạ bậc sin cos có ứng dụng gì trong thực tế?
Công thức hạ bậc sin cos có nhiều ứng dụng trong vật lý, kỹ thuật, toán học và đồ họa máy tính.
5. Tôi có thể tìm thêm tài liệu về công thức hạ bậc sin cos ở đâu?
Bạn có thể tìm thêm tài liệu trong sách giáo khoa, sách tham khảo, các trang web giáo dục trực tuyến và tic.edu.vn.
6. Tic.edu.vn có những tài liệu gì về lượng giác?
Tic.edu.vn cung cấp đầy đủ các công thức, bài tập, ví dụ minh họa về công thức hạ bậc sin cos và các chủ đề lượng giác khác.
7. Tôi có thể hỏi đáp thắc mắc về lượng giác ở đâu trên tic.edu.vn?
Bạn có thể tham gia cộng đồng học tập trên tic.edu.vn để trao đổi, thảo luận và nhận được sự hỗ trợ từ những người khác.
8. Học lượng giác trên tic.edu.vn có mất phí không?
Không, tất cả các tài liệu và công cụ trên tic.edu.vn đều được cung cấp miễn phí.
9. Tic.edu.vn có những ưu điểm gì so với các website học toán khác?
Tic.edu.vn có tài liệu phong phú, kiến thức cập nhật, giao diện thân thiện, cộng đồng hỗ trợ và hoàn toàn miễn phí.
10. Làm sao để liên hệ với tic.edu.vn nếu tôi có thắc mắc hoặc góp ý?
Bạn có thể liên hệ với tic.edu.vn qua email: [email protected].
Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn mong muốn có một cộng đồng học tập để trao đổi kiến thức và kinh nghiệm? Hãy đến với tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, đa dạng và được kiểm duyệt kỹ lưỡng. Tic.edu.vn sẽ là người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn.
Truy cập website: tic.edu.vn hoặc liên hệ qua email: [email protected] để được tư vấn và hỗ trợ tốt nhất.