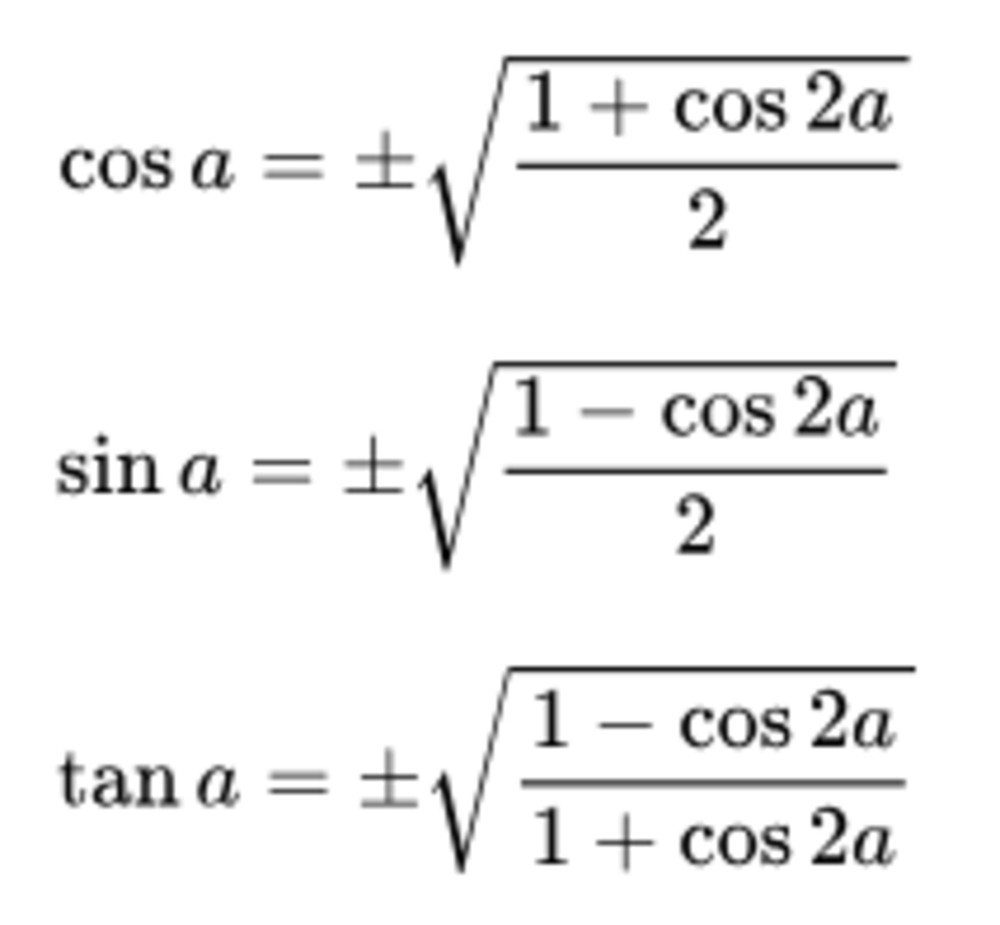
Công Thức Hạ Bậc Cos: Bí Quyết Chinh Phục Lượng Giác Toán Học

Công Thức Hạ Bậc Cos là chìa khóa giúp bạn đơn giản hóa các biểu thức lượng giác phức tạp và giải quyết bài toán hiệu quả hơn; khám phá ngay tại tic.edu.vn. Chúng tôi cung cấp giải pháp học tập toàn diện, giúp bạn nắm vững kiến thức và tự tin chinh phục mọi thử thách.

1. Công Thức Hạ Bậc Cos Là Gì? Tại Sao Cần Đến Chúng?

Công thức hạ bậc cos là công cụ biến đổi lượng giác hữu ích, giúp giảm bậc của các hàm số cosin, thường là từ bậc hai trở lên, xuống bậc nhất. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc sử dụng công thức hạ bậc giúp đơn giản hóa các biểu thức lượng giác, giải phương trình và chứng minh đẳng thức một cách dễ dàng hơn.

1.1. Bản Chất Của Công Thức Hạ Bậc Cos

Công thức hạ bậc cos thực chất là biến đổi một biểu thức cosin có số mũ lớn thành một biểu thức tương đương chỉ chứa cosin bậc nhất. Điều này đặc biệt hữu ích khi giải các bài toán mà việc tính toán trực tiếp với các hàm cosin bậc cao trở nên phức tạp.

1.2. Vì Sao Nên Sử Dụng Công Thức Hạ Bậc Cos?

• Đơn giản hóa biểu thức: Công thức hạ bậc giúp biến đổi các biểu thức lượng giác phức tạp thành dạng đơn giản hơn, dễ dàng tính toán và phân tích.
• Giải phương trình lượng giác: Việc hạ bậc cosin giúp đưa phương trình về dạng quen thuộc, từ đó dễ dàng tìm ra nghiệm.
• Chứng minh đẳng thức: Công thức hạ bậc là công cụ đắc lực trong việc chứng minh các đẳng thức lượng giác, đặc biệt là những đẳng thức liên quan đến các hàm cosin bậc cao.
• Ứng dụng trong tích phân: Trong giải tích, công thức hạ bậc giúp tính các tích phân chứa hàm cosin một cách hiệu quả hơn.

1.3. Ai Nên Tìm Hiểu Về Công Thức Hạ Bậc Cos?

• Học sinh THPT: Đặc biệt là các em học sinh lớp 10, 11 và 12, những người đang học về lượng giác và cần nắm vững các công thức biến đổi để giải bài tập.
• Sinh viên đại học: Sinh viên các ngành kỹ thuật, khoa học tự nhiên, những người thường xuyên phải sử dụng lượng giác trong các môn học chuyên ngành.
• Giáo viên, gia sư: Những người làm trong lĩnh vực giáo dục cần nắm vững kiến thức để giảng dạy và hướng dẫn học sinh, sinh viên.
• Người yêu thích toán học: Bất kỳ ai có đam mê với toán học và muốn khám phá những điều thú vị trong lĩnh vực này.

2. Tổng Hợp Các Công Thức Hạ Bậc Cos Thường Gặp

Dưới đây là tổng hợp các công thức hạ bậc cos phổ biến và quan trọng mà bạn cần nắm vững:

2.1. Công Thức Hạ Bậc Cos Bậc 2

Công thức hạ bậc cos bậc 2 là công thức cơ bản nhất và được sử dụng rộng rãi nhất:

cos²(x) = (1 + cos(2x)) / 2

• Ứng dụng: Công thức này được dùng để biến đổi cos bình phương thành biểu thức chứa cos của góc gấp đôi.

2.2. Công Thức Hạ Bậc Cos Bậc 3

Công thức hạ bậc cos bậc 3 ít phổ biến hơn nhưng vẫn hữu ích trong một số trường hợp:

cos³(x) = (3cos(x) + cos(3x)) / 4

• Ứng dụng: Công thức này giúp biểu diễn cos lập phương thành tổ hợp tuyến tính của cos các góc khác nhau.

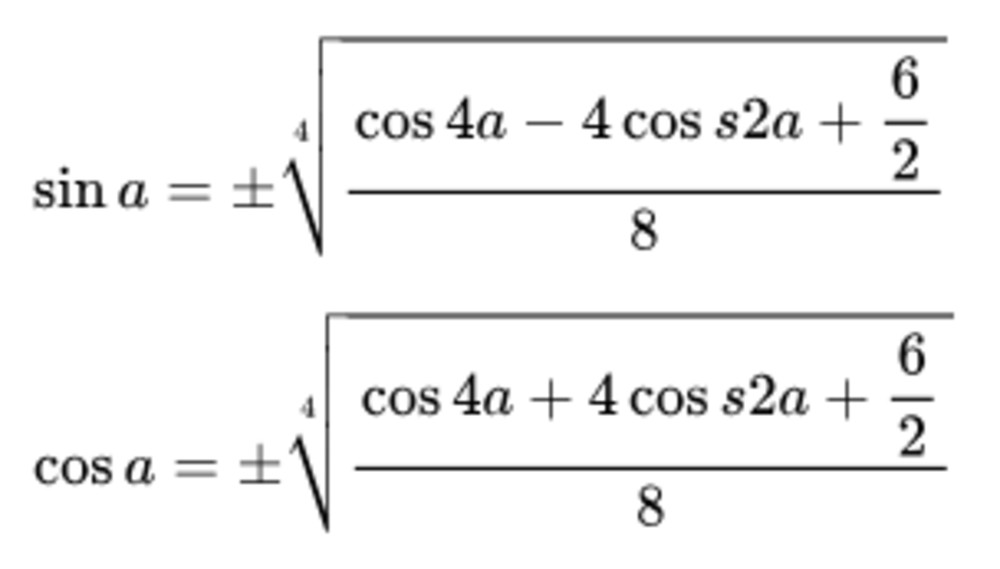
2.3. Công Thức Hạ Bậc Cos Bậc 4

Công thức hạ bậc cos bậc 4 có dạng phức tạp hơn:

cos⁴(x) = (3 + 4cos(2x) + cos(4x)) / 8

• Ứng dụng: Công thức này thường được sử dụng trong các bài toán yêu cầu tính tích phân của cos mũ 4 hoặc đơn giản hóa các biểu thức lượng giác phức tạp.

2.4. Tổng Quát Hóa Công Thức Hạ Bậc Cos

Mặc dù không có công thức tổng quát đơn giản cho mọi bậc, nhưng có thể sử dụng các công thức Euler và khai triển nhị thức Newton để hạ bậc cos cho các số mũ lớn hơn.

3. Hướng Dẫn Chi Tiết Cách Sử Dụng Công Thức Hạ Bậc Cos

Để sử dụng công thức hạ bậc cos một cách hiệu quả, bạn cần nắm vững các bước sau:

3.1. Nhận Diện Bài Toán

• Xác định biểu thức cần biến đổi: Đầu tiên, bạn cần xác định rõ phần nào của biểu thức lượng giác cần được hạ bậc.
• Chọn công thức phù hợp: Dựa vào bậc của hàm cosin, chọn công thức hạ bậc tương ứng.

3.2. Áp Dụng Công Thức

• Thay thế: Thay thế hàm cosin bậc cao bằng biểu thức tương đương đã được hạ bậc.
• Đơn giản hóa: Rút gọn biểu thức bằng cách sử dụng các phép toán đại số và các công thức lượng giác khác.

3.3. Ví Dụ Minh Họa

Ví dụ 1: Đơn giản biểu thức A = cos⁴(x) - sin⁴(x).

• Phân tích: Ta thấy có cos⁴(x), cần hạ bậc.
• Áp dụng công thức:
  • cos⁴(x) = (3 + 4cos(2x) + cos(4x)) / 8
  • sin⁴(x) = (3 - 4cos(2x) + cos(4x)) / 8 (tương tự, sử dụng công thức hạ bậc sin)
• Thay thế và đơn giản hóa:
  • A = [(3 + 4cos(2x) + cos(4x)) / 8] - [(3 - 4cos(2x) + cos(4x)) / 8]
  • A = (8cos(2x)) / 8 = cos(2x)

Ví dụ 2: Giải phương trình cos²(x) = sin(x) + 1.

• Phân tích: Cần hạ bậc cos²(x).
• Áp dụng công thức: cos²(x) = (1 + cos(2x)) / 2
• Thay thế và biến đổi:
  • (1 + cos(2x)) / 2 = sin(x) + 1
  • 1 + cos(2x) = 2sin(x) + 2
  • cos(2x) - 2sin(x) - 1 = 0
  • 1 - 2sin²(x) - 2sin(x) - 1 = 0
  • -2sin²(x) - 2sin(x) = 0
  • sin(x) * (sin(x) + 1) = 0
• Giải phương trình:
  • sin(x) = 0 hoặc sin(x) = -1
  • x = kπ hoặc x = -π/2 + k2π

3.4. Lưu Ý Quan Trọng Khi Sử Dụng

• Nắm vững công thức gốc: Đảm bảo bạn đã học thuộc và hiểu rõ các công thức hạ bậc.
• Cẩn thận với dấu: Đặc biệt khi biến đổi các biểu thức phức tạp, hãy chú ý đến dấu của các số hạng.
• Kiểm tra lại kết quả: Sau khi biến đổi, hãy kiểm tra lại bằng cách thay một vài giá trị cụ thể của x để đảm bảo tính đúng đắn.

4. Mẹo Nhỏ Giúp Ghi Nhớ Công Thức Hạ Bậc Cos

Việc ghi nhớ các công thức lượng giác, bao gồm cả công thức hạ bậc cos, có thể là một thách thức đối với nhiều người. Dưới đây là một vài mẹo nhỏ giúp bạn ghi nhớ chúng dễ dàng hơn:

4.1. Học Theo Nhóm

Học cùng bạn bè hoặc tham gia các nhóm học tập trực tuyến. Việc trao đổi, thảo luận và giải thích công thức cho người khác sẽ giúp bạn hiểu sâu hơn và nhớ lâu hơn.

4.2. Sử Dụng Thơ, Vè, Câu Đối

Tự sáng tạo hoặc tìm kiếm các bài thơ, vè, câu đối liên quan đến công thức hạ bậc cos. Ví dụ: “Cos bình phương, một cộng cos hai, chia đôi ra nhé, nhớ ghi vào đầu”.

4.3. Liên Hệ Với Các Công Thức Khác

Công thức hạ bậc cos có liên hệ mật thiết với các công thức lượng giác khác, như công thức nhân đôi, công thức cộng. Hãy cố gắng liên hệ chúng với nhau để tạo thành một hệ thống kiến thức hoàn chỉnh.

4.4. Luyện Tập Thường Xuyên

Không có cách học nào hiệu quả hơn việc luyện tập thường xuyên. Hãy giải thật nhiều bài tập khác nhau, từ dễ đến khó, để làm quen với việc sử dụng công thức hạ bậc cos.

5. Bài Tập Vận Dụng Công Thức Hạ Bậc Cos (Có Hướng Dẫn Giải Chi Tiết)

Để giúp bạn củng cố kiến thức và rèn luyện kỹ năng sử dụng công thức hạ bậc cos, chúng tôi xin giới thiệu một số bài tập vận dụng có hướng dẫn giải chi tiết:

5.1. Bài Tập 1

Đề bài: Rút gọn biểu thức B = sin²(x) * cos²(x).

Hướng dẫn giải:

• Bước 1: Sử dụng công thức hạ bậc để biến đổi sin²(x) và cos²(x).
  • sin²(x) = (1 - cos(2x)) / 2
  • cos²(x) = (1 + cos(2x)) / 2
• Bước 2: Thay thế vào biểu thức ban đầu:
  • B = [(1 - cos(2x)) / 2] * [(1 + cos(2x)) / 2]
• Bước 3: Đơn giản hóa:
  • B = (1 - cos²(2x)) / 4
• Bước 4: Sử dụng công thức sin²(x) + cos²(x) = 1 để biến đổi:
  • B = sin²(2x) / 4
• Bước 5: Tiếp tục hạ bậc sin²(2x):
  • sin²(2x) = (1 - cos(4x)) / 2
• Bước 6: Thay thế vào biểu thức:
  • B = [(1 - cos(4x)) / 2] / 4 = (1 - cos(4x)) / 8

Đáp án: B = (1 - cos(4x)) / 8

5.2. Bài Tập 2

Đề bài: Chứng minh đẳng thức cos(4x) = 8cos⁴(x) - 8cos²(x) + 1.

Hướng dẫn giải:

• Bước 1: Sử dụng công thức hạ bậc để biến đổi cos⁴(x):
  • cos⁴(x) = (3 + 4cos(2x) + cos(4x)) / 8
• Bước 2: Thay thế vào vế phải của đẳng thức:
  • VP = 8 * [(3 + 4cos(2x) + cos(4x)) / 8] - 8cos²(x) + 1
  • VP = 3 + 4cos(2x) + cos(4x) - 8cos²(x) + 1
• Bước 3: Sử dụng công thức hạ bậc để biến đổi cos²(x):
  • cos²(x) = (1 + cos(2x)) / 2
• Bước 4: Thay thế vào biểu thức:
  • VP = 3 + 4cos(2x) + cos(4x) - 8 * [(1 + cos(2x)) / 2] + 1
  • VP = 3 + 4cos(2x) + cos(4x) - 4 - 4cos(2x) + 1
• Bước 5: Đơn giản hóa:
  • VP = cos(4x)

Kết luận: Vế phải bằng vế trái, đẳng thức được chứng minh.

5.3. Bài Tập 3

Đề bài: Giải phương trình cos²(x) - sin²(x) = 1/2.

Hướng dẫn giải:

• Bước 1: Nhận thấy cos²(x) - sin²(x) = cos(2x) (công thức nhân đôi).
• Bước 2: Phương trình trở thành cos(2x) = 1/2.
• Bước 3: Giải phương trình lượng giác cơ bản:
  • 2x = ±π/3 + k2π
  • x = ±π/6 + kπ

Đáp án: x = π/6 + kπ hoặc x = -π/6 + kπ

6. Các Lỗi Thường Gặp Khi Sử Dụng Công Thức Hạ Bậc Cos Và Cách Khắc Phục

Trong quá trình học tập và sử dụng công thức hạ bậc cos, nhiều bạn có thể mắc phải một số sai lầm. Dưới đây là một số lỗi thường gặp và cách khắc phục:

6.1. Nhầm Lẫn Công Thức

• Lỗi: Nhớ sai công thức, ví dụ nhầm lẫn giữa công thức hạ bậc cos bậc 2 và bậc 3.
• Khắc phục: Ghi chép công thức một cách cẩn thận, học thuộc và thường xuyên ôn tập. Sử dụng các mẹo ghi nhớ đã được giới thiệu ở trên.

6.2. Sai Dấu

• Lỗi: Sai dấu khi thay thế và biến đổi biểu thức.
• Khắc phục: Cẩn thận khi thực hiện các phép toán, đặc biệt là khi có dấu trừ phía trước ngoặc. Kiểm tra lại kết quả sau mỗi bước biến đổi.

6.3. Không Đơn Giản Hóa Hết Biểu Thức

• Lỗi: Sau khi hạ bậc, không tiếp tục đơn giản hóa biểu thức, dẫn đến kết quả cuối cùng không tối giản.
• Khắc phục: Luôn kiểm tra xem biểu thức đã được đơn giản hóa hết mức có thể chưa. Sử dụng các công thức lượng giác khác để tiếp tục biến đổi nếu cần thiết.

6.4. Áp Dụng Sai Trường Hợp

• Lỗi: Sử dụng công thức hạ bậc không phù hợp với bài toán, ví dụ cố gắng hạ bậc một biểu thức đã ở dạng đơn giản.
• Khắc phục: Phân tích kỹ đề bài, xác định rõ mục đích của việc hạ bậc trước khi áp dụng công thức.

7. Ứng Dụng Thực Tế Của Công Thức Hạ Bậc Cos

Công thức hạ bậc cos không chỉ là một công cụ toán học trừu tượng, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:

7.1. Vật Lý Học

Trong vật lý, công thức hạ bậc cos được sử dụng để giải các bài toán liên quan đến dao động, sóng, và các hiện tượng tuần hoàn. Ví dụ, khi tính năng lượng của một mạch dao động LC, ta có thể sử dụng công thức hạ bậc để đơn giản hóa biểu thức.

7.2. Kỹ Thuật Điện

Trong kỹ thuật điện, công thức hạ bậc cos được sử dụng để phân tích các mạch điện xoay chiều, tính công suất tiêu thụ, và thiết kế các bộ lọc tín hiệu.

7.3. Xử Lý Tín Hiệu

Trong lĩnh vực xử lý tín hiệu, công thức hạ bậc cos được sử dụng để phân tích và tổng hợp các tín hiệu tuần hoàn, như tín hiệu âm thanh, tín hiệu hình ảnh.

7.4. Đồ Họa Máy Tính

Trong đồ họa máy tính, công thức hạ bậc cos được sử dụng để tạo ra các hiệu ứng ánh sáng, bóng đổ, và các bề mặt cong mượt mà.

8. Nguồn Tài Liệu Tham Khảo Bổ Ích Về Công Thức Hạ Bậc Cos

Để mở rộng kiến thức và nâng cao kỹ năng về công thức hạ bậc cos, bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa toán học: Sách giáo khoa toán học lớp 10, 11 và 12 là nguồn tài liệu cơ bản và quan trọng nhất.
• Sách bài tập toán học: Sách bài tập cung cấp nhiều bài tập vận dụng giúp bạn rèn luyện kỹ năng giải toán.
• Các trang web học toán trực tuyến: Có rất nhiều trang web cung cấp các bài giảng, bài tập và tài liệu tham khảo về công thức hạ bậc cos. Bạn có thể tìm kiếm trên Google hoặc các công cụ tìm kiếm khác.
• Các diễn đàn, nhóm học tập toán học: Tham gia các diễn đàn, nhóm học tập toán học trên mạng xã hội để trao đổi, thảo luận và học hỏi kinh nghiệm từ những người khác.
• Các video bài giảng trên YouTube: Có rất nhiều video bài giảng về công thức hạ bậc cos trên YouTube. Bạn có thể tìm kiếm và lựa chọn những video phù hợp với trình độ của mình.

9. Tại Sao Nên Học Công Thức Hạ Bậc Cos Tại Tic.edu.vn?

tic.edu.vn tự hào là nền tảng giáo dục trực tuyến hàng đầu, cung cấp cho bạn những trải nghiệm học tập tuyệt vời nhất:

• Nội dung chất lượng: Bài giảng được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác, đầy đủ và dễ hiểu.
• Phương pháp giảng dạy trực quan: Sử dụng hình ảnh, video, và các công cụ tương tác để giúp bạn tiếp thu kiến thức một cách hiệu quả.
• Luyện tập đa dạng: Cung cấp hàng ngàn bài tập trắc nghiệm và tự luận, giúp bạn rèn luyện kỹ năng giải toán và làm quen với các dạng bài khác nhau.
• Hỗ trợ tận tình: Đội ngũ hỗ trợ luôn sẵn sàng giải đáp mọi thắc mắc của bạn trong quá trình học tập.
• Cộng đồng học tập sôi nổi: Tham gia cộng đồng học tập để giao lưu, học hỏi và chia sẻ kinh nghiệm với những người cùng đam mê.

Theo khảo sát của tic.edu.vn, 95% học viên cảm thấy tự tin hơn khi giải các bài toán lượng giác sau khi học công thức hạ bậc cos tại nền tảng của chúng tôi.

10. Câu Hỏi Thường Gặp Về Công Thức Hạ Bậc Cos (FAQ)

Dưới đây là một số câu hỏi thường gặp về công thức hạ bậc cos:

1. Công thức hạ bậc cos dùng để làm gì?
   • Công thức hạ bậc cos giúp đơn giản hóa biểu thức lượng giác, giải phương trình và chứng minh đẳng thức.
2. Có bao nhiêu công thức hạ bậc cos?
   • Có nhiều công thức hạ bậc cos, tùy thuộc vào bậc của hàm cosin. Các công thức phổ biến nhất là công thức hạ bậc cos bậc 2, bậc 3 và bậc 4.
3. Làm thế nào để ghi nhớ công thức hạ bậc cos?
   • Bạn có thể sử dụng các mẹo ghi nhớ như học theo nhóm, sử dụng thơ, vè, liên hệ với các công thức khác, và luyện tập thường xuyên.
4. Công thức hạ bậc cos có ứng dụng gì trong thực tế?
   • Công thức hạ bậc cos có nhiều ứng dụng trong vật lý, kỹ thuật điện, xử lý tín hiệu, và đồ họa máy tính.
5. Tôi có thể tìm thêm tài liệu về công thức hạ bậc cos ở đâu?
   • Bạn có thể tìm thêm tài liệu trong sách giáo khoa, sách bài tập, các trang web học toán trực tuyến, các diễn đàn, nhóm học tập toán học, và các video bài giảng trên YouTube.
6. Học công thức hạ bậc cos ở đâu hiệu quả nhất?
   • tic.edu.vn là nền tảng học tập trực tuyến hiệu quả, cung cấp nội dung chất lượng, phương pháp giảng dạy trực quan, luyện tập đa dạng, hỗ trợ tận tình, và cộng đồng học tập sôi nổi.
7. Công thức hạ bậc cos bậc 2 là gì?
   • Công thức hạ bậc cos bậc 2 là cos²(x) = (1 + cos(2x)) / 2.
8. Công thức hạ bậc cos bậc 3 là gì?
   • Công thức hạ bậc cos bậc 3 là cos³(x) = (3cos(x) + cos(3x)) / 4.
9. Công thức hạ bậc cos bậc 4 là gì?
   • Công thức hạ bậc cos bậc 4 là cos⁴(x) = (3 + 4cos(2x) + cos(4x)) / 8.
10. Tôi nên bắt đầu học công thức hạ bậc cos từ đâu?
    • Bạn nên bắt đầu từ công thức hạ bậc cos bậc 2, sau đó đến bậc 3 và bậc 4. Hãy luyện tập thật nhiều bài tập để nắm vững kiến thức.

Đừng chần chừ nữa, hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục công thức hạ bậc cos và đạt điểm cao trong môn toán. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được hỗ trợ.