**Công Thức Diện Tích Tam Giác:** Tổng Hợp Chi Tiết & Ứng Dụng

Công Thức Diện Tích Tam Giác là kiến thức toán học quan trọng, được ứng dụng rộng rãi trong giải toán và các lĩnh vực khác. Hãy cùng khám phá các công thức tính diện tích tam giác đầy đủ nhất tại tic.edu.vn, giúp bạn học tập và áp dụng hiệu quả. Bài viết này cung cấp kiến thức toàn diện, từ định nghĩa đến các dạng bài tập nâng cao, cùng những ví dụ minh họa dễ hiểu.

1. Khám Phá Thế Giới Hình Tam Giác

Trước khi đi sâu vào các công thức, chúng ta hãy cùng nhau tìm hiểu về hình tam giác, một hình học cơ bản nhưng vô cùng thú vị.

1.1. Định Nghĩa Về Hình Tam Giác

Hình tam giác là một đa giác có ba cạnh và ba đỉnh. Các cạnh nối các đỉnh tạo thành hình dạng đặc trưng của tam giác, và góc giữa các cạnh được gọi là góc của tam giác. Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc hiểu rõ định nghĩa này là nền tảng để tiếp cận các bài toán liên quan đến tam giác một cách hiệu quả.

Hình tam giác là gì?

1.2. Phân Loại Các Loại Tam Giác

Tam giác có thể được phân loại dựa trên độ dài cạnh và số đo góc, tạo nên sự đa dạng trong hình học:

• Theo cạnh:
  • Tam giác đều: Ba cạnh bằng nhau, ba góc bằng nhau (60 độ).
  • Tam giác cân: Ít nhất hai cạnh bằng nhau.
  • Tam giác thường: Ba cạnh khác nhau.
• Theo góc:
  • Tam giác nhọn: Ba góc đều nhọn (nhỏ hơn 90 độ).
  • Tam giác tù: Một góc tù (lớn hơn 90 độ).
  • Tam giác vuông: Một góc vuông (90 độ).
• Kết hợp: Tam giác vuông cân (vừa vuông, vừa cân).

1.3. Tính Chất Quan Trọng Của Tam Giác

Để giải quyết các bài toán hình học, bạn cần nắm vững các tính chất sau:

1. Tổng các góc: Tổng ba góc trong một tam giác luôn bằng 180 độ. Đây là định lý cơ bản, được sử dụng rộng rãi trong các bài toán chứng minh và tính toán.
2. Góc ngoài: Mỗi góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
3. Bất đẳng thức tam giác: Tổng độ dài hai cạnh bất kỳ luôn lớn hơn cạnh còn lại.
4. Định lý Pythagoras: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông (a² + b² = c²).
5. Đường phân giác: Đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề.
6. Đường trung tuyến: Ba đường trung tuyến của tam giác cắt nhau tại trọng tâm, điểm này chia mỗi đường trung tuyến thành hai đoạn, đoạn gần đỉnh bằng 2/3 độ dài đường trung tuyến.
7. Chu vi và diện tích: Chu vi là tổng độ dài ba cạnh. Diện tích có thể được tính bằng nhiều công thức khác nhau, tùy thuộc vào loại tam giác và thông tin đã biết.

2. Tổng Hợp Các Công Thức Diện Tích Tam Giác

Diện tích tam giác có thể được tính bằng nhiều công thức khác nhau, tùy thuộc vào thông tin đã biết. Hãy cùng tic.edu.vn khám phá những công thức này:

Tổng hợp 6 công thức tính diện tích tam giác chi tiết

2.1. Công Thức Diện Tích Tam Giác Thường

Tam giác thường là tam giác có ba cạnh với độ dài khác nhau và ba góc với số đo khác nhau.

• Công thức cơ bản:

  Diện tích tam giác thường được tính bằng nửa tích của một cạnh và chiều cao tương ứng với cạnh đó.

  Công thức: S = (1/2) a h

  Trong đó:

  • S là diện tích tam giác.
  • a là độ dài cạnh đáy.
  • h là chiều cao tương ứng với cạnh đáy a.

  Ví dụ: Tam giác ABC có cạnh BC = 8cm, chiều cao AH = 5cm. Diện tích tam giác ABC là: S = (1/2) 8 5 = 20 cm².

• Công thức Heron (khi biết ba cạnh):

  Nếu bạn biết độ dài ba cạnh của tam giác, bạn có thể sử dụng công thức Heron để tính diện tích.

  Công thức: S = √[p(p – a)(p – b)(p – c)]

  Trong đó:

  • a, b, c là độ dài ba cạnh của tam giác.
  • p là nửa chu vi của tam giác, được tính bằng: p = (a + b + c) / 2

  Ví dụ: Tam giác ABC có AB = 5cm, BC = 7cm, CA = 8cm. Nửa chu vi p = (5 + 7 + 8) / 2 = 10cm. Diện tích tam giác ABC là: S = √[10(10 – 5)(10 – 7)(10 – 8)] = √(10 5 3 * 2) = √300 ≈ 17.32 cm².

• Công thức sử dụng định lý sin (khi biết hai cạnh và góc xen giữa):

  Nếu bạn biết độ dài hai cạnh và góc xen giữa chúng, bạn có thể sử dụng công thức này để tính diện tích.

  Công thức: S = (1/2) a b * sin(C)

  Trong đó:

  • a, b là độ dài hai cạnh của tam giác.
  • C là góc xen giữa hai cạnh a và b.

  Ví dụ: Tam giác ABC có AB = 6cm, AC = 9cm, góc A = 60°. Diện tích tam giác ABC là: S = (1/2) 6 9 sin(60°) = (1/2) 6 9 (√3 / 2) ≈ 23.38 cm².

2.2. Cách Tính Diện Tích Tam Giác Vuông

Tam giác vuông là tam giác có một góc vuông (90 độ). Cạnh đối diện với góc vuông được gọi là cạnh huyền, hai cạnh còn lại là cạnh góc vuông.

Công thức tính diện tích tam giác vuông rất đơn giản:

S = (1/2) a b

Trong đó:

• a, b là độ dài hai cạnh góc vuông.

Ví dụ: Tam giác ABC vuông tại A có AB = 4cm, AC = 7cm. Diện tích tam giác ABC là: S = (1/2) 4 7 = 14 cm².

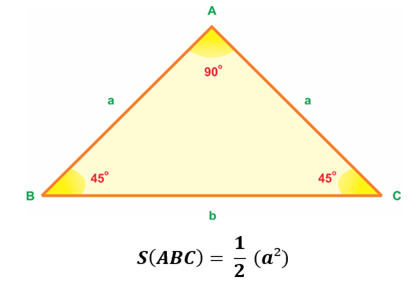
2.3. Công Thức Diện Tích Tam Giác Vuông Cân

Tam giác vuông cân là tam giác vừa vuông, vừa cân. Điều này có nghĩa là nó có một góc vuông và hai cạnh góc vuông bằng nhau.

Công thức tính diện tích tam giác vuông cân:

S = (1/2) * a²

Trong đó:

• a là độ dài cạnh góc vuông.

Công thức diện tích tam giác vuông cân đầy đủ

Ví dụ: Tam giác ABC vuông cân tại A có AB = AC = 5cm. Diện tích tam giác ABC là: S = (1/2) * 5² = 12.5 cm².

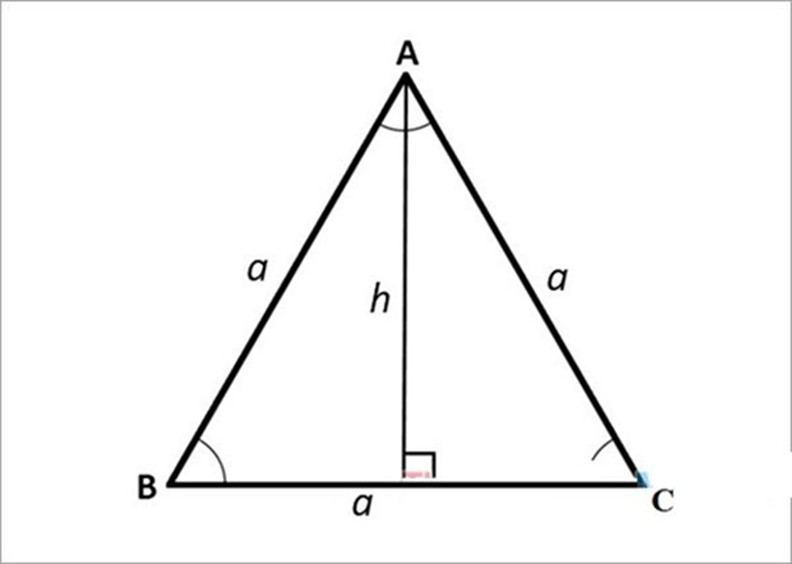
2.4. Cách Tính Diện Tích Tam Giác Cân

Tam giác cân là tam giác có hai cạnh bằng nhau. Cạnh còn lại được gọi là cạnh đáy.

Để tính diện tích tam giác cân, ta cần biết độ dài cạnh đáy và chiều cao tương ứng.

Công thức: S = (1/2) a h

Trong đó:

• a là độ dài cạnh đáy.
• h là chiều cao hạ từ đỉnh xuống cạnh đáy.

Ví dụ: Tam giác ABC cân tại A có BC = 6cm, chiều cao AH = 4cm. Diện tích tam giác ABC là: S = (1/2) 6 4 = 12 cm².

2.5. Công Thức Diện Tích Tam Giác Đều

Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (60 độ).

Công thức tính diện tích tam giác đều:

S = (√3 / 4) * a²

Trong đó:

• a là độ dài cạnh của tam giác đều.

Công thức tính diện tích tam giác đều cạnh a

Ví dụ: Tam giác ABC đều có AB = BC = CA = 4cm. Diện tích tam giác ABC là: S = (√3 / 4) * 4² = 4√3 ≈ 6.93 cm².

2.6. Công Thức Tính Diện Tích Tam Giác Trong Oxyz

Trong không gian Oxyz, tam giác được xác định bởi ba điểm không thẳng hàng. Để tính diện tích tam giác, ta sử dụng tích có hướng của hai vectơ tạo bởi ba điểm đó.

Công thức:

S = (1/2) * |[AB, AC]|

Trong đó:

• A(x₁, y₁, z₁), B(x₂, y₂, z₂), C(x₃, y₃, z₃) là tọa độ ba đỉnh của tam giác.
• AB = (x₂ – x₁, y₂ – y₁, z₂ – z₁) và AC = (x₃ – x₁, y₃ – y₁, z₃ – z₁) là hai vectơ tạo bởi ba điểm.
• [AB, AC] là tích có hướng của hai vectơ AB và AC.
• |[AB, AC]| là độ dài của vectơ tích có hướng.

Ví dụ: Cho tam giác ABC có A(1, 0, 1), B(2, 1, 3), C(0, 2, -1).

• AB = (1, 1, 2)
• AC = (-1, 2, -2)
• [AB, AC] = (-6, 0, 3)
• |[AB, AC]| = √(36 + 0 + 9) = √45 = 3√5
• S = (1/2) * 3√5 ≈ 3.35

3. Các Dạng Bài Tập Diện Tích Tam Giác Thường Gặp

Để nắm vững các công thức, hãy cùng tic.edu.vn luyện tập với các dạng bài tập thường gặp:

3.1. Bài Tập Khi Biết Cạnh Đáy Và Chiều Cao

Đây là dạng bài tập cơ bản nhất. Bạn chỉ cần áp dụng công thức S = (1/2) a h.

Ví dụ: Tam giác ABC có cạnh đáy BC = 10cm, chiều cao AH = 6cm. Tính diện tích tam giác ABC.

Lời giải: S = (1/2) 10 6 = 30 cm².

3.2. Bài Tập Khi Biết Độ Dài Ba Cạnh

Trong trường hợp này, bạn cần sử dụng công thức Heron.

Ví dụ: Tam giác ABC có AB = 5cm, BC = 6cm, CA = 7cm. Tính diện tích tam giác ABC.

Lời giải:

• p = (5 + 6 + 7) / 2 = 9cm
• S = √[9(9 – 5)(9 – 6)(9 – 7)] = √(9 4 3 * 2) = √216 ≈ 14.70 cm².

3.3. Bài Tập Với Tam Giác Đều

Bạn có thể sử dụng công thức S = (√3 / 4) * a² hoặc tìm chiều cao rồi áp dụng công thức cơ bản.

Ví dụ: Tam giác ABC đều có cạnh AB = 8cm. Tính diện tích tam giác ABC.

Lời giải:

• S = (√3 / 4) * 8² = 16√3 ≈ 27.71 cm².
• Hoặc, chiều cao h = a√3 / 2 = 8√3 / 2 = 4√3. S = (1/2) 8 4√3 = 16√3 ≈ 27.71 cm².

3.4. Bài Tập Với Tọa Độ Oxyz

Bạn cần tìm tọa độ các vectơ, tính tích có hướng và độ dài của nó.

Ví dụ: Cho tam giác ABC có A(1, 1, 1), B(2, 3, 1), C(1, 2, 2). Tính diện tích tam giác ABC.

Lời giải:

• AB = (1, 2, 0)
• AC = (0, 1, 1)
• [AB, AC] = (2, -1, 1)
• |[AB, AC]| = √(4 + 1 + 1) = √6
• S = (1/2) * √6 ≈ 1.22

3.5. Bài Tập Tìm Cạnh Khi Biết Diện Tích

Bạn cần biến đổi công thức diện tích để tìm cạnh cần thiết.

Ví dụ: Tam giác vuông ABC vuông tại A có diện tích S = 20 cm², cạnh AB = 5cm. Tính độ dài cạnh AC.

Lời giải: S = (1/2) AB AC => AC = (2 S) / AB = (2 20) / 5 = 8 cm.

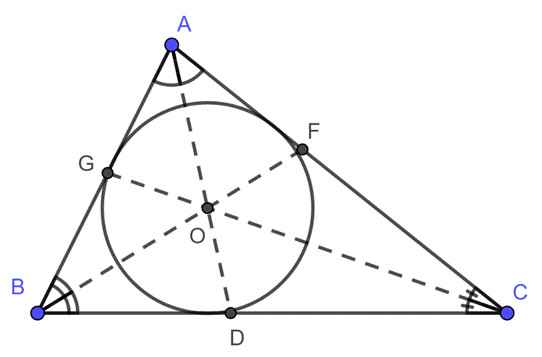
3.6. Bài Tập Với Chu Vi Và Bán Kính Đường Tròn Nội Tiếp

Sử dụng công thức S = (p * r), trong đó p là nửa chu vi và r là bán kính đường tròn nội tiếp.

Để tính diện tích tam giác khi biết chu vi (P) và bán kính đường tròn nội tiếp (r), ta sử dụng một công thức liên quan đến tam giác và đường tròn nội tiếp.

Đặt a, b và c lần lượt là ba cạnh của tam giác và R là bán kính đường tròn ngoại tiếp tam giác (được tính bằng ba đỉnh của tam giác). Ta có các mối quan hệ sau:

1. Diện tích tam giác (S) và bán kính đường tròn ngoại tiếp (R):

S = (abc) / (4R)

2. Diện tích tam giác (S) và chu vi (P):

S = (P * r) / 2

Ví dụ: Tam giác ABC có chu vi P = 24cm, bán kính đường tròn nội tiếp r = 2cm. Tính diện tích tam giác ABC.

Lời giải:

• p = P / 2 = 24 / 2 = 12cm
• S = p r = 12 2 = 24 cm².

4. Bài Tập Mẫu Với Lời Giải Chi Tiết

Để giúp bạn hiểu rõ hơn, tic.edu.vn xin giới thiệu một số bài tập điển hình:

4.1. Bài Tập 1

Tam giác ABC vuông tại A, có chiều cao AH = 4cm. Cạnh góc vuông AB = 6cm. Tính diện tích tam giác ABC.

Lời giải:

• Vì tam giác ABC vuông tại A, ta có thể sử dụng công thức S = (1/2) AB AC.
• Để tìm AC, ta sử dụng định lý Pythagoras: BC² = AB² + AC² => AC = √(BC² – AB²).
• Tuy nhiên, ta không biết BC. Thay vào đó, ta sử dụng công thức S = (1/2) AB AH.
• S = (1/2) 6 4 = 12 cm².

4.2. Bài Tập 2

Tam giác ABC có ba cạnh AB = 7cm, BC = 9cm, CA = 12cm. Tính diện tích tam giác ABC.

Lời giải:

• Sử dụng công thức Heron: p = (7 + 9 + 12) / 2 = 14cm.
• S = √[14(14 – 7)(14 – 9)(14 – 12)] = √(14 7 5 * 2) = √980 ≈ 31.30 cm².

4.3. Bài Tập 3

Tam giác ABC có chu vi P = 40cm và bán kính đường tròn nội tiếp r = 3cm. Tính diện tích tam giác ABC.

Lời giải:

• Sử dụng công thức S = p * r, với p = P / 2 = 40 / 2 = 20cm.
• S = 20 * 3 = 60 cm².

5. Câu Hỏi Thường Gặp

5.1. Làm Sao Để Tính Diện Tích Tam Giác Lớp 5?

Công thức tính diện tích tam giác lớp 5 là S = (1/2) a h, trong đó a là cạnh đáy và h là chiều cao tương ứng.

5.2. Tính Diện Tích Tam Giác Khi Biết 3 Cạnh Như Thế Nào?

Sử dụng công thức Heron: S = √[p(p – a)(p – b)(p – c)], trong đó a, b, c là độ dài ba cạnh và p là nửa chu vi.

6. Kết Luận

Với những kiến thức và công thức được tổng hợp chi tiết tại tic.edu.vn, hy vọng bạn đã nắm vững cách tính diện tích tam giác trong mọi trường hợp. Hãy luyện tập thường xuyên để nâng cao kỹ năng giải toán và áp dụng kiến thức vào thực tế. Nếu bạn gặp bất kỳ khó khăn nào, đừng ngần ngại liên hệ với chúng tôi qua email: [email protected] hoặc truy cập website: tic.edu.vn để được hỗ trợ.

Khám phá thêm nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả tại tic.edu.vn ngay hôm nay! Đừng bỏ lỡ cơ hội kết nối với cộng đồng học tập sôi nổi và nâng cao kiến thức của bạn.

Thông tin liên hệ:

• Email: [email protected]
• Trang web: tic.edu.vn