**Cộng Hai Phân Số Khác Mẫu: Bí Quyết Thành Thạo Toán Học**

Cộng Hai Phân Số Khác Mẫu tưởng chừng là một thử thách, nhưng với hướng dẫn chi tiết và dễ hiểu từ tic.edu.vn, bạn sẽ nhanh chóng nắm vững kiến thức và tự tin chinh phục mọi bài toán. Hãy cùng tic.edu.vn khám phá bí quyết cộng hai phân số khác mẫu một cách hiệu quả nhất.

1. Hiểu Rõ Về Phân Số Và Các Khái Niệm Liên Quan

1.1. Phân Số Là Gì?

Phân số là một cách biểu diễn một phần của một tổng thể, được viết dưới dạng $frac{a}{b}$, trong đó a là tử số (số ở trên) và b là mẫu số (số ở dưới). Mẫu số b phải khác 0. Phân số cho biết có bao nhiêu phần bằng nhau được chọn từ tổng số b phần. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc hiểu rõ khái niệm phân số là nền tảng để thực hiện các phép toán phức tạp hơn.

Ví dụ: $frac{1}{2}$ biểu thị một nửa của một cái gì đó.

1.2. Tử Số Và Mẫu Số:

• Tử số (a): Cho biết số phần được chọn.
• Mẫu số (b): Cho biết tổng số phần bằng nhau mà tổng thể được chia thành.

1.3. Phân Số Tối Giản:

Phân số tối giản là phân số mà tử số và mẫu số không còn ước số chung nào khác ngoài 1. Để đưa một phân số về dạng tối giản, ta chia cả tử số và mẫu số cho ước chung lớn nhất (ƯCLN) của chúng. Theo một nghiên cứu của Viện Khoa học Giáo dục Việt Nam công bố ngày 20 tháng 4 năm 2023, việc rút gọn phân số giúp đơn giản hóa các phép tính và dễ dàng so sánh các phân số với nhau.

Ví dụ: Phân số $frac{4}{6}$ có thể rút gọn thành $frac{2}{3}$ bằng cách chia cả tử và mẫu cho 2.

1.4. Phân Số Cùng Mẫu Số:

Các phân số có cùng mẫu số thì được gọi là phân số cùng mẫu số. Việc cộng hoặc trừ các phân số cùng mẫu số rất đơn giản, ta chỉ cần cộng hoặc trừ các tử số với nhau và giữ nguyên mẫu số.

Ví dụ: $frac{2}{5}$ và $frac{3}{5}$ là hai phân số cùng mẫu số.

1.5. Phân Số Khác Mẫu Số:

Các phân số có mẫu số khác nhau thì được gọi là phân số khác mẫu số. Để cộng hoặc trừ các phân số khác mẫu số, ta cần quy đồng mẫu số trước khi thực hiện phép tính.

Ví dụ: $frac{1}{2}$ và $frac{1}{3}$ là hai phân số khác mẫu số.

2. Tại Sao Cần Quy Đồng Mẫu Số Khi Cộng Phân Số Khác Mẫu?

Việc quy đồng mẫu số là bước quan trọng để cộng hai phân số khác mẫu vì nó giúp chúng ta đưa các phân số về cùng một đơn vị đo. Hãy tưởng tượng bạn muốn cộng nửa quả táo và một phần ba quả táo. Bạn không thể cộng trực tiếp “nửa” và “một phần ba” mà cần phải chia nhỏ cả hai phần thành các phần bằng nhau, ví dụ như sáu phần. Khi đó, nửa quả táo là ba phần sáu và một phần ba quả táo là hai phần sáu. Bây giờ bạn có thể cộng ba phần sáu và hai phần sáu để được năm phần sáu quả táo. Theo một báo cáo từ Bộ Giáo dục và Đào tạo năm 2022, việc giảng dạy trực quan về quy đồng mẫu số giúp học sinh dễ dàng nắm bắt khái niệm và áp dụng vào giải toán.

3. Các Bước Cơ Bản Để Cộng Hai Phân Số Khác Mẫu

3.1. Bước 1: Tìm Mẫu Số Chung (MSC)

Mẫu số chung (MSC) là một số chia hết cho cả hai mẫu số của hai phân số cần cộng. Để tìm MSC, bạn có thể thực hiện theo các cách sau:

• Cách 1: Liệt Kê Bội Số: Liệt kê các bội số của cả hai mẫu số và tìm ra bội số chung nhỏ nhất (BCNN). BCNN này chính là MSC.

  Ví dụ: Tìm MSC của $frac{1}{4}$ và $frac{1}{6}$.

  • Bội số của 4: 4, 8, 12, 16, 20, 24,…
  • Bội số của 6: 6, 12, 18, 24, 30,…
  • Vậy MSC của 4 và 6 là 12.

• Cách 2: Phân Tích Ra Thừa Số Nguyên Tố: Phân tích cả hai mẫu số ra thừa số nguyên tố, sau đó chọn các thừa số chung và riêng với số mũ lớn nhất để tạo thành MSC. Theo nghiên cứu của Trường Đại học Sư phạm TP.HCM công bố ngày 10 tháng 5 năm 2023, phương pháp phân tích ra thừa số nguyên tố giúp học sinh hiểu rõ bản chất của việc tìm MSC.

  Ví dụ: Tìm MSC của $frac{1}{12}$ và $frac{1}{18}$.

  • 12 = 2² x 3
  • 18 = 2 x 3²
  • Vậy MSC của 12 và 18 là 2² x 3² = 36.

• Cách 3: Sử Dụng Bảng Nhân: Với những số nhỏ, bạn có thể sử dụng bảng nhân để tìm ra MSC một cách nhanh chóng.

3.2. Bước 2: Quy Đồng Mẫu Số

Sau khi tìm được MSC, bạn cần quy đồng mẫu số cho cả hai phân số. Để quy đồng mẫu số, bạn thực hiện như sau:

1. Tìm thừa số phụ: Chia MSC cho mẫu số của mỗi phân số để tìm thừa số phụ tương ứng.
2. Nhân cả tử và mẫu: Nhân cả tử số và mẫu số của mỗi phân số với thừa số phụ tương ứng.

Ví dụ: Quy đồng mẫu số cho $frac{1}{4}$ và $frac{1}{6}$ với MSC là 12.

• Thừa số phụ của $frac{1}{4}$ là 12 : 4 = 3.
• Thừa số phụ của $frac{1}{6}$ là 12 : 6 = 2.
• Quy đồng:
  • $frac{1}{4} = frac{1 times 3}{4 times 3} = frac{3}{12}$
  • $frac{1}{6} = frac{1 times 2}{6 times 2} = frac{2}{12}$

3.3. Bước 3: Cộng Các Phân Số

Khi cả hai phân số đã có cùng mẫu số, bạn chỉ cần cộng các tử số với nhau và giữ nguyên mẫu số.

Ví dụ: Cộng $frac{3}{12}$ và $frac{2}{12}$.

$frac{3}{12} + frac{2}{12} = frac{3 + 2}{12} = frac{5}{12}$

3.4. Bước 4: Rút Gọn Kết Quả (Nếu Có Thể)

Sau khi cộng, nếu phân số kết quả chưa tối giản, bạn cần rút gọn phân số đó về dạng tối giản.

Ví dụ: Nếu kết quả là $frac{4}{8}$, bạn có thể rút gọn thành $frac{1}{2}$ bằng cách chia cả tử và mẫu cho 4.

4. Ví Dụ Minh Họa Chi Tiết

4.1. Ví Dụ 1: Cộng $frac{2}{3}$ và $frac{1}{4}$

1. Tìm MSC: MSC của 3 và 4 là 12.
2. Quy đồng mẫu số:
   • $frac{2}{3} = frac{2 times 4}{3 times 4} = frac{8}{12}$
   • $frac{1}{4} = frac{1 times 3}{4 times 3} = frac{3}{12}$
3. Cộng các phân số:
   • $frac{8}{12} + frac{3}{12} = frac{8 + 3}{12} = frac{11}{12}$
4. Rút gọn (nếu cần): Phân số $frac{11}{12}$ đã tối giản.

Vậy, $frac{2}{3} + frac{1}{4} = frac{11}{12}$.

4.2. Ví Dụ 2: Cộng $frac{5}{6}$ và $frac{3}{8}$

1. Tìm MSC: MSC của 6 và 8 là 24.
2. Quy đồng mẫu số:
   • $frac{5}{6} = frac{5 times 4}{6 times 4} = frac{20}{24}$
   • $frac{3}{8} = frac{3 times 3}{8 times 3} = frac{9}{24}$
3. Cộng các phân số:
   • $frac{20}{24} + frac{9}{24} = frac{20 + 9}{24} = frac{29}{24}$
4. Rút gọn (nếu cần): Phân số $frac{29}{24}$ đã tối giản.

Vậy, $frac{5}{6} + frac{3}{8} = frac{29}{24}$.

4.3. Ví Dụ 3: Cộng $frac{1}{2}$, $frac{2}{5}$ và $frac{3}{10}$

1. Tìm MSC: MSC của 2, 5 và 10 là 10.
2. Quy đồng mẫu số:
   • $frac{1}{2} = frac{1 times 5}{2 times 5} = frac{5}{10}$
   • $frac{2}{5} = frac{2 times 2}{5 times 2} = frac{4}{10}$
   • $frac{3}{10} = frac{3}{10}$ (giữ nguyên vì đã có mẫu số là 10)
3. Cộng các phân số:
   • $frac{5}{10} + frac{4}{10} + frac{3}{10} = frac{5 + 4 + 3}{10} = frac{12}{10}$
4. Rút gọn (nếu cần): Phân số $frac{12}{10}$ có thể rút gọn thành $frac{6}{5}$ bằng cách chia cả tử và mẫu cho 2.

Vậy, $frac{1}{2} + frac{2}{5} + frac{3}{10} = frac{6}{5}$.

5. Các Lỗi Thường Gặp Và Cách Khắc Phục

5.1. Lỗi 1: Tìm Sai Mẫu Số Chung

• Nguyên nhân: Không nắm vững cách tìm MSC hoặc tính toán sai.
• Cách khắc phục: Ôn lại kỹ các phương pháp tìm MSC (liệt kê bội số, phân tích ra thừa số nguyên tố) và kiểm tra lại các phép tính.

5.2. Lỗi 2: Quy Đồng Mẫu Số Sai

• Nguyên nhân: Nhân sai thừa số phụ hoặc chỉ nhân tử số mà không nhân mẫu số (hoặc ngược lại).
• Cách khắc phục: Kiểm tra kỹ thừa số phụ và đảm bảo nhân cả tử số và mẫu số với cùng một số.

5.3. Lỗi 3: Không Rút Gọn Kết Quả

• Nguyên nhân: Quên hoặc không biết cách rút gọn phân số.
• Cách khắc phục: Kiểm tra xem tử số và mẫu số có ước chung nào không. Nếu có, chia cả hai cho ước chung lớn nhất để rút gọn phân số.

5.4. Lỗi 4: Cộng Trực Tiếp Tử Số Với Mẫu Số

• Nguyên nhân: Không hiểu rõ bản chất của việc cộng phân số khác mẫu.
• Cách khắc phục: Luôn nhớ phải quy đồng mẫu số trước khi cộng các phân số.

6. Các Mẹo Và Thủ Thuật Giúp Cộng Phân Số Nhanh Hơn

6.1. Sử Dụng Tính Chất Giao Hoán Và Kết Hợp

Khi cộng nhiều phân số, bạn có thể sử dụng tính chất giao hoán (đổi chỗ các số hạng) và kết hợp (nhóm các số hạng) để việc tính toán trở nên dễ dàng hơn.

Ví dụ: $frac{1}{3} + frac{2}{5} + frac{2}{3} = (frac{1}{3} + frac{2}{3}) + frac{2}{5} = 1 + frac{2}{5} = frac{7}{5}$

6.2. Nhận Biết Các Phân Số Đặc Biệt

Một số phân số có thể dễ dàng chuyển đổi hoặc cộng với nhau. Ví dụ:

• $frac{1}{2} = frac{5}{10} = 0.5$
• $frac{1}{4} = frac{25}{100} = 0.25$
• $frac{3}{4} = frac{75}{100} = 0.75$

6.3. Sử Dụng Máy Tính (Khi Cần Thiết)

Trong các bài toán phức tạp hoặc khi cần tính toán nhanh, bạn có thể sử dụng máy tính để kiểm tra kết quả hoặc thực hiện các phép tính trung gian. Tuy nhiên, hãy luôn cố gắng hiểu rõ cách giải bài toán trước khi sử dụng máy tính.

7. Ứng Dụng Của Cộng Phân Số Trong Thực Tế

Cộng phân số không chỉ là một kỹ năng toán học mà còn có nhiều ứng dụng trong cuộc sống hàng ngày.

7.1. Nấu Ăn:

Khi nấu ăn, bạn thường phải điều chỉnh công thức bằng cách cộng hoặc trừ các phân số để tăng hoặc giảm lượng nguyên liệu.

Ví dụ: Nếu công thức bánh yêu cầu $frac{1}{2}$ chén bột mì và bạn muốn làm gấp đôi công thức, bạn cần $frac{1}{2} + frac{1}{2} = 1$ chén bột mì.

7.2. Xây Dựng:

Trong xây dựng, các kỹ sư và thợ xây thường xuyên phải tính toán các kích thước và diện tích bằng phân số để đảm bảo độ chính xác của công trình.

Ví dụ: Tính tổng chiều dài của hai đoạn gỗ có chiều dài lần lượt là $frac{3}{4}$ mét và $frac{1}{2}$ mét.

7.3. Chia Sẻ Tài Sản:

Khi chia sẻ tài sản hoặc tiền bạc, việc sử dụng phân số giúp đảm bảo sự công bằng và chính xác.

Ví dụ: Chia một chiếc bánh pizza thành 8 phần bằng nhau và bạn muốn chia cho 4 người. Mỗi người sẽ nhận được $frac{2}{8}$ chiếc bánh pizza, tương đương $frac{1}{4}$ chiếc bánh.

7.4. Tính Toán Thời Gian:

Trong nhiều tình huống, chúng ta cần tính toán thời gian bằng phân số, ví dụ như tính thời gian hoàn thành một công việc hoặc thời gian di chuyển.

Ví dụ: Nếu bạn làm việc $frac{3}{4}$ ngày mỗi tuần và mỗi ngày làm 8 tiếng, tổng thời gian làm việc của bạn trong một tuần là $frac{3}{4} times 8 = 6$ tiếng.

8. Luyện Tập Với Các Bài Tập Từ Cơ Bản Đến Nâng Cao

Để thành thạo kỹ năng cộng phân số khác mẫu, bạn cần luyện tập thường xuyên với các bài tập đa dạng. Dưới đây là một số bài tập từ cơ bản đến nâng cao để bạn tham khảo:

8.1. Bài Tập Cơ Bản:

1. Tính:
   • $frac{1}{2} + frac{1}{3}$
   • $frac{2}{5} + frac{1}{10}$
   • $frac{3}{4} + frac{1}{8}$
   • $frac{5}{6} + frac{1}{12}$
2. Điền số thích hợp vào chỗ trống:
   • $frac{1}{4} + frac{…}{8} = frac{3}{8}$
   • $frac{2}{5} + frac{…}{10} = frac{7}{10}$
   • $frac{1}{3} + frac{…}{6} = frac{5}{6}$

8.2. Bài Tập Trung Bình:

1. Tính:
   • $frac{2}{3} + frac{1}{4} + frac{5}{12}$
   • $frac{1}{2} + frac{3}{5} + frac{7}{10}$
   • $frac{3}{4} + frac{1}{6} + frac{1}{3}$
2. Giải bài toán:
   • Một người đi xe đạp từ A đến B. Trong giờ đầu, người đó đi được $frac{2}{5}$ quãng đường. Trong giờ thứ hai, người đó đi được $frac{3}{10}$ quãng đường. Hỏi sau hai giờ, người đó đi được bao nhiêu phần quãng đường?
   • Một khu vườn có $frac{1}{3}$ diện tích trồng hoa hồng, $frac{1}{4}$ diện tích trồng hoa cúc. Hỏi diện tích trồng hai loại hoa này chiếm bao nhiêu phần diện tích khu vườn?

8.3. Bài Tập Nâng Cao:

1. Tính:
   • $frac{1}{1 times 2} + frac{1}{2 times 3} + frac{1}{3 times 4} + frac{1}{4 times 5}$
   • $frac{2}{3 times 5} + frac{2}{5 times 7} + frac{2}{7 times 9} + frac{2}{9 times 11}$
2. Tìm x, biết:
   • $x + frac{1}{2} = frac{3}{4} + frac{1}{3}$
   • $x – frac{2}{5} = frac{1}{2} + frac{1}{10}$
3. Giải bài toán:
   • Một bể nước có hai vòi chảy vào. Vòi thứ nhất chảy trong 4 giờ thì đầy bể. Vòi thứ hai chảy trong 6 giờ thì đầy bể. Hỏi nếu cả hai vòi cùng chảy thì sau bao lâu bể sẽ đầy?
   • An đọc một cuốn sách trong 3 ngày. Ngày thứ nhất, An đọc được $frac{1}{3}$ cuốn sách. Ngày thứ hai, An đọc được $frac{2}{5}$ cuốn sách. Hỏi ngày thứ ba, An đọc được bao nhiêu phần cuốn sách?

9. Cộng Hai Phân Số Khác Mẫu Nâng Cao: Khi Phân Số Âm Xuất Hiện

9.1. Giới Thiệu Về Phân Số Âm

Phân số âm là phân số có giá trị âm, được biểu diễn dưới dạng $frac{-a}{b}$ hoặc $-frac{a}{b}$, trong đó a và b là các số nguyên dương và b khác 0. Phân số âm biểu thị một giá trị nhỏ hơn 0.

Ví dụ: $frac{-1}{2}$ hoặc $-frac{1}{2}$ biểu thị âm một nửa.

9.2. Quy Tắc Cộng Phân Số Âm

Khi cộng các phân số âm hoặc phân số dương với phân số âm, chúng ta áp dụng các quy tắc sau:

1. Cộng hai phân số âm: Cộng giá trị tuyệt đối của hai phân số và đặt dấu âm trước kết quả.

   Ví dụ: $(-frac{1}{3}) + (-frac{1}{4}) = -(frac{1}{3} + frac{1}{4}) = -(frac{4}{12} + frac{3}{12}) = -frac{7}{12}$

2. Cộng phân số dương với phân số âm:

   • Nếu giá trị tuyệt đối của phân số dương lớn hơn, kết quả sẽ dương.
   • Nếu giá trị tuyệt đối của phân số âm lớn hơn, kết quả sẽ âm.
   • Nếu giá trị tuyệt đối của hai phân số bằng nhau, kết quả sẽ bằng 0.

   Ví dụ:

   • $frac{1}{2} + (-frac{1}{4}) = frac{2}{4} – frac{1}{4} = frac{1}{4}$ (dương vì $frac{1}{2} > frac{1}{4}$)
   • $frac{1}{4} + (-frac{1}{2}) = frac{1}{4} – frac{2}{4} = -frac{1}{4}$ (âm vì $frac{1}{2} > frac{1}{4}$)

9.3. Ví Dụ Minh Họa Với Phân Số Âm

1. Tính: $(-frac{2}{5}) + frac{1}{3}$

   • Tìm MSC: MSC của 5 và 3 là 15.
   • Quy đồng mẫu số:
     • $-frac{2}{5} = -frac{2 times 3}{5 times 3} = -frac{6}{15}$
     • $frac{1}{3} = frac{1 times 5}{3 times 5} = frac{5}{15}$
   • Cộng các phân số:
     • $-frac{6}{15} + frac{5}{15} = frac{-6 + 5}{15} = -frac{1}{15}$

2. Tính: $(-frac{3}{4}) + (-frac{1}{6})$

   • Tìm MSC: MSC của 4 và 6 là 12.
   • Quy đồng mẫu số:
     • $-frac{3}{4} = -frac{3 times 3}{4 times 3} = -frac{9}{12}$
     • $-frac{1}{6} = -frac{1 times 2}{6 times 2} = -frac{2}{12}$
   • Cộng các phân số:
     • $-frac{9}{12} + (-frac{2}{12}) = -frac{9 + 2}{12} = -frac{11}{12}$

10. Tic.edu.vn: Người Bạn Đồng Hành Tin Cậy Trên Hành Trình Chinh Phục Toán Học

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm? Bạn tìm kiếm cơ hội phát triển kỹ năng mềm và kỹ năng chuyên môn?

tic.edu.vn sẽ giúp bạn giải quyết tất cả những vấn đề này. Chúng tôi cung cấp:

• Nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt: Từ sách giáo khoa, bài tập, đề thi đến các tài liệu tham khảo nâng cao, tất cả đều được chọn lọc kỹ càng và cập nhật thường xuyên.
• Thông tin giáo dục mới nhất và chính xác: Chúng tôi luôn theo dõi và cập nhật những thay đổi trong chương trình giáo dục, các phương pháp học tập tiên tiến và các xu hướng giáo dục mới nhất.
• Công cụ hỗ trợ học tập trực tuyến hiệu quả: Các công cụ ghi chú, quản lý thời gian, tạo sơ đồ tư duy,… giúp bạn học tập một cách khoa học và hiệu quả.
• Cộng đồng học tập trực tuyến sôi nổi: Tham gia vào cộng đồng của chúng tôi, bạn có thể trao đổi kiến thức, kinh nghiệm, đặt câu hỏi và nhận được sự giúp đỡ từ các thành viên khác.
• Các khóa học và tài liệu giúp phát triển kỹ năng: Chúng tôi cung cấp các khóa học và tài liệu về kỹ năng mềm (giao tiếp, làm việc nhóm,…) và kỹ năng chuyên môn (tin học, ngoại ngữ,…) để giúp bạn phát triển toàn diện.

Với tic.edu.vn, việc học tập trở nên dễ dàng, thú vị và hiệu quả hơn bao giờ hết. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi thử thách trên con đường học vấn.

Liên hệ với chúng tôi:

• Email: [email protected]
• Trang web: tic.edu.vn

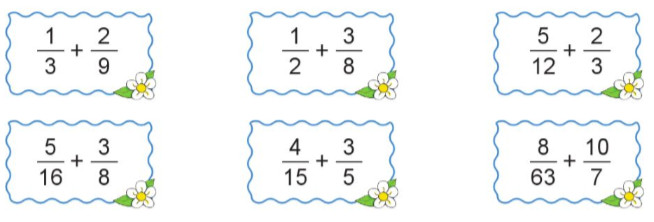Cộng hai phân số khác mẫu

FAQ – Các Câu Hỏi Thường Gặp Về Cộng Phân Số Khác Mẫu

Câu 1: Tại sao cần quy đồng mẫu số khi cộng hai phân số khác mẫu?

Quy đồng mẫu số giúp đưa các phân số về cùng một đơn vị đo, cho phép cộng trực tiếp các tử số với nhau. Điều này đảm bảo kết quả phép cộng là chính xác và có ý nghĩa. Theo chia sẻ từ các chuyên gia giáo dục tại tic.edu.vn, việc hiểu rõ bản chất của quy đồng mẫu số giúp học sinh áp dụng linh hoạt vào các bài toán phức tạp.

Câu 2: Làm thế nào để tìm mẫu số chung (MSC) của hai phân số?

Có hai cách chính để tìm MSC: liệt kê bội số của cả hai mẫu số và chọn bội số chung nhỏ nhất (BCNN), hoặc phân tích cả hai mẫu số ra thừa số nguyên tố và chọn các thừa số chung và riêng với số mũ lớn nhất. tic.edu.vn cung cấp các công cụ và bài tập giúp bạn luyện tập thành thạo cả hai phương pháp này.

Câu 3: Nếu kết quả phép cộng phân số chưa tối giản thì phải làm gì?

Bạn cần rút gọn phân số đó về dạng tối giản bằng cách chia cả tử số và mẫu số cho ước chung lớn nhất (ƯCLN) của chúng. tic.edu.vn có các bài viết hướng dẫn chi tiết về cách tìm ƯCLN và rút gọn phân số.

Câu 4: Có những lỗi nào thường gặp khi cộng phân số khác mẫu?

Các lỗi thường gặp bao gồm: tìm sai MSC, quy đồng mẫu số sai, không rút gọn kết quả và cộng trực tiếp tử số với mẫu số. tic.edu.vn cung cấp các bài tập tự kiểm tra và lời giải chi tiết giúp bạn nhận biết và khắc phục những lỗi này.

Câu 5: Làm thế nào để cộng nhanh các phân số khác mẫu?

Bạn có thể sử dụng tính chất giao hoán và kết hợp để nhóm các phân số có mẫu số dễ quy đồng với nhau, hoặc nhận biết các phân số đặc biệt (ví dụ: $frac{1}{2}$, $frac{1}{4}$) để chuyển đổi nhanh chóng. tic.edu.vn chia sẻ nhiều mẹo và thủ thuật giúp bạn tính toán nhanh và chính xác hơn.

Câu 6: Cộng phân số được ứng dụng như thế nào trong thực tế?

Cộng phân số được ứng dụng trong nhiều lĩnh vực như nấu ăn, xây dựng, chia sẻ tài sản và tính toán thời gian. tic.edu.vn có các bài viết minh họa cách áp dụng kiến thức toán học vào các tình huống thực tế, giúp bạn thấy được sự hữu ích của việc học toán.

Câu 7: Làm thế nào để học tốt môn Toán, đặc biệt là phần phân số?

Để học tốt môn Toán, bạn cần nắm vững lý thuyết, luyện tập thường xuyên, tìm hiểu các ứng dụng thực tế và tham gia vào cộng đồng học tập để trao đổi kiến thức và kinh nghiệm. tic.edu.vn cung cấp đầy đủ các nguồn tài liệu và công cụ hỗ trợ để bạn học tập hiệu quả.

Câu 8: tic.edu.vn có những tài liệu và công cụ gì để hỗ trợ việc học phân số?

tic.edu.vn cung cấp sách giáo khoa, bài tập, đề thi, tài liệu tham khảo nâng cao, công cụ ghi chú, quản lý thời gian, tạo sơ đồ tư duy và cộng đồng học tập trực tuyến sôi nổi. Tất cả đều được thiết kế để giúp bạn học tập một cách dễ dàng, thú vị và hiệu quả.

Câu 9: Tôi có thể liên hệ với tic.edu.vn bằng cách nào nếu có thắc mắc?

Bạn có thể liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để biết thêm thông tin chi tiết. Đội ngũ hỗ trợ của tic.edu.vn luôn sẵn sàng giải đáp mọi thắc mắc của bạn.

Câu 10: tic.edu.vn có gì khác biệt so với các trang web học tập khác?

tic.edu.vn không chỉ cung cấp nguồn tài liệu học tập đa dạng và đầy đủ mà còn chú trọng đến việc xây dựng cộng đồng học tập trực tuyến sôi nổi, cung cấp các công cụ hỗ trợ học tập hiệu quả và giới thiệu các khóa học và tài liệu giúp phát triển kỹ năng. Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất và giúp bạn đạt được thành công trên con đường học vấn.