**Chu Vi Hình Thang: Công Thức, Bài Tập, Mẹo Nhớ Dành Cho Mọi Học Sinh**

Chu vi hình thang là một khái niệm quan trọng trong hình học, giúp bạn giải quyết các bài toán liên quan đến đo lường và tính toán. Để giúp bạn nắm vững kiến thức này, tic.edu.vn cung cấp một hướng dẫn chi tiết về công thức tính chu vi hình thang, các dạng bài tập thường gặp và mẹo ghi nhớ hữu ích. Khám phá ngay những bí quyết giúp bạn chinh phục mọi bài toán hình thang một cách dễ dàng và hiệu quả.

1. Tổng Quan Về Chu Vi Hình Thang

Chu vi hình thang là tổng độ dài của tất cả các cạnh của nó. Việc nắm vững công thức tính chu vi sẽ giúp bạn giải quyết nhanh chóng và chính xác các bài toán liên quan đến hình thang.

1.1. Định Nghĩa Hình Thang

Hình thang là một tứ giác có ít nhất một cặp cạnh đối diện song song với nhau. Cặp cạnh song song này được gọi là cạnh đáy của hình thang, hai cạnh còn lại được gọi là cạnh bên. Theo định nghĩa của Math Open Reference, hình thang là một tứ giác lồi có hai cạnh song song.

1.2. Các Loại Hình Thang Thường Gặp

Có ba loại hình thang thường gặp là hình thang thường, hình thang vuông và hình thang cân. Mỗi loại có những đặc điểm và công thức tính chu vi riêng.

• Hình Thang Thường: Là hình thang có bốn cạnh với độ dài khác nhau và không có góc vuông.
• Hình Thang Vuông: Là hình thang có ít nhất một góc vuông (tức là một cạnh bên vuông góc với cả hai đáy).
• Hình Thang Cân: Là hình thang có hai cạnh bên bằng nhau.

2. Công Thức Tính Chu Vi Hình Thang Chi Tiết

Để tính chu vi hình thang, chúng ta sẽ xem xét từng loại hình thang cụ thể.

2.1. Công Thức Tính Chu Vi Hình Thang Thường

Chu vi hình thang thường được tính bằng cách cộng độ dài của cả bốn cạnh lại với nhau.

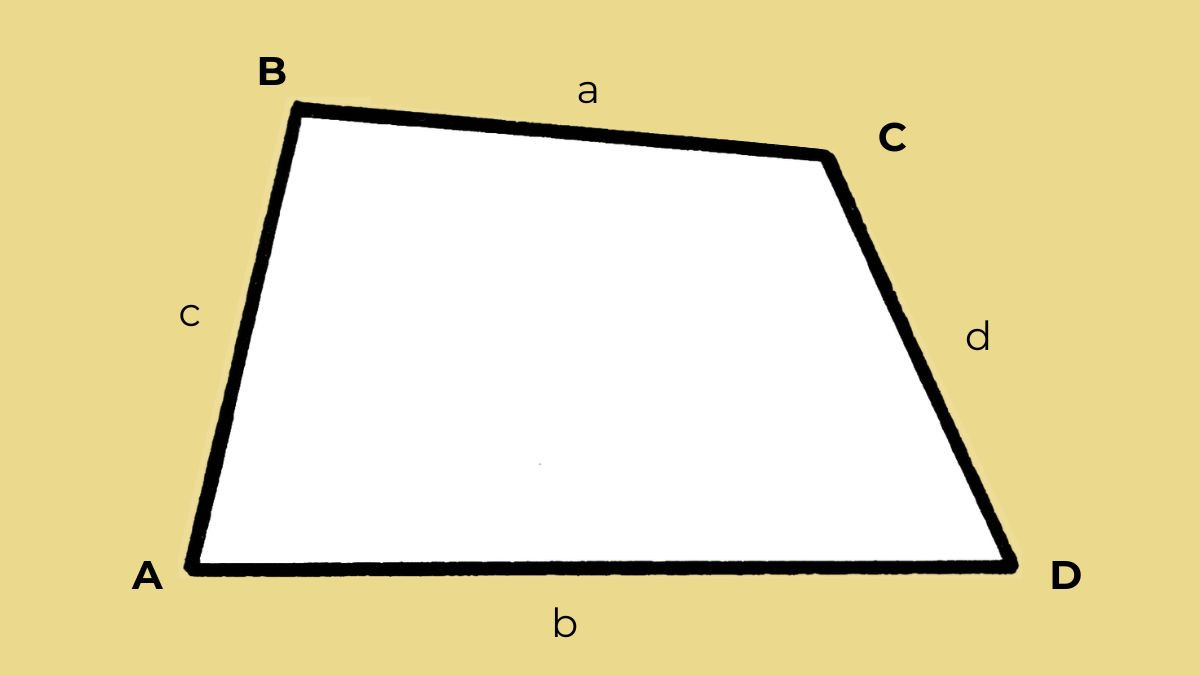
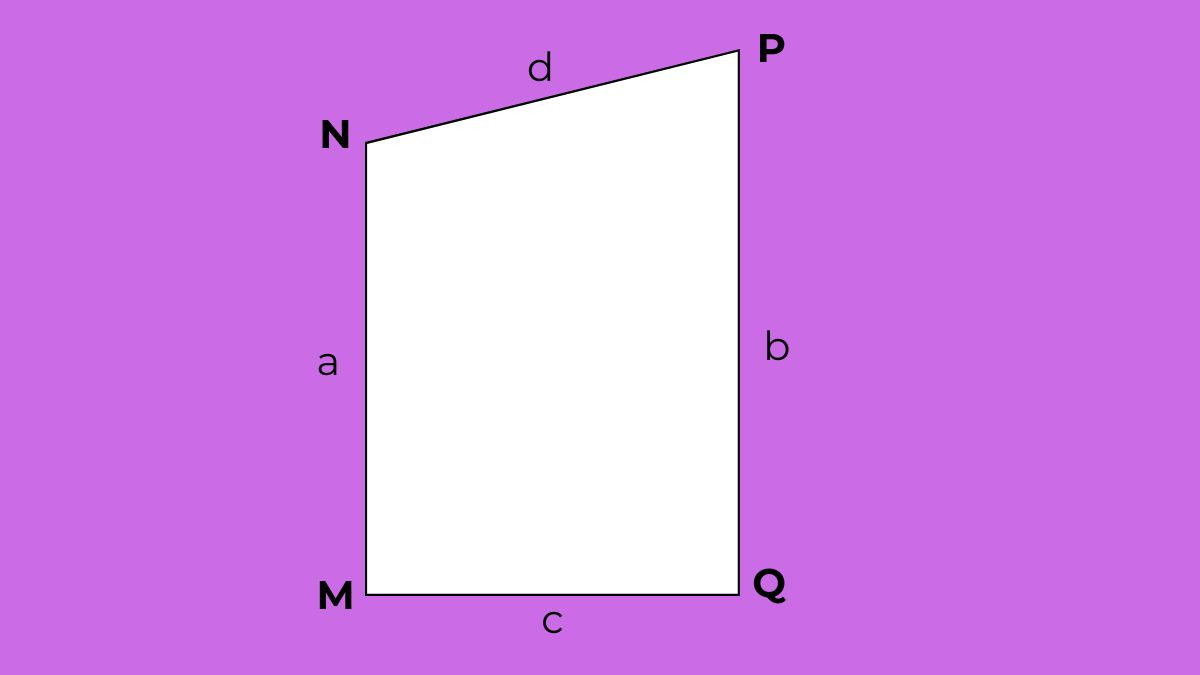
• Công Thức: P = a + b + c + d

Trong đó:

• P: Chu vi của hình thang
• a và b: Độ dài của hai cạnh đáy
• c và d: Độ dài của hai cạnh bên

Alt: Minh họa công thức tính chu vi hình thang thường với các cạnh a, b, c, d.

Ví dụ: Cho hình thang ABCD có cạnh đáy AB = 5cm, cạnh đáy CD = 8cm, cạnh bên AD = 4cm và cạnh bên BC = 6cm. Tính chu vi hình thang ABCD.

Giải:

Áp dụng công thức, ta có: P = 5 + 8 + 4 + 6 = 23cm.

2.2. Công Thức Tính Chu Vi Hình Thang Vuông

Hình thang vuông là hình thang có một cạnh bên vuông góc với cả hai cạnh đáy. Công thức tính chu vi hình thang vuông cũng tương tự như hình thang thường, bằng tổng độ dài của bốn cạnh.

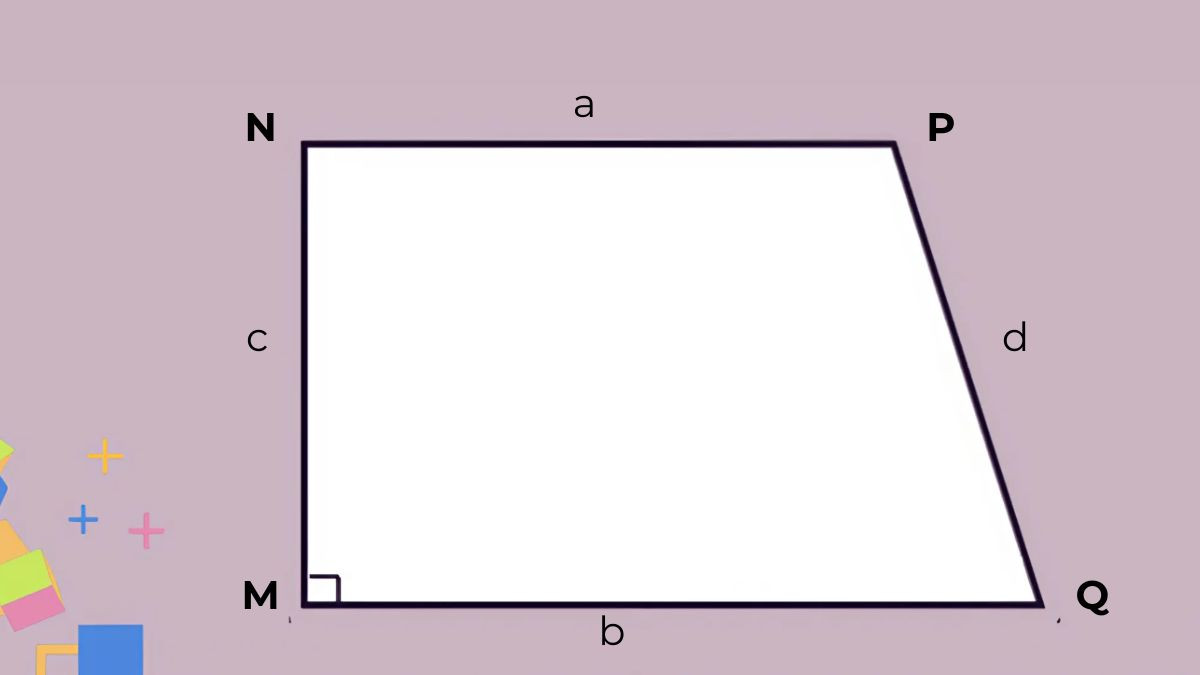
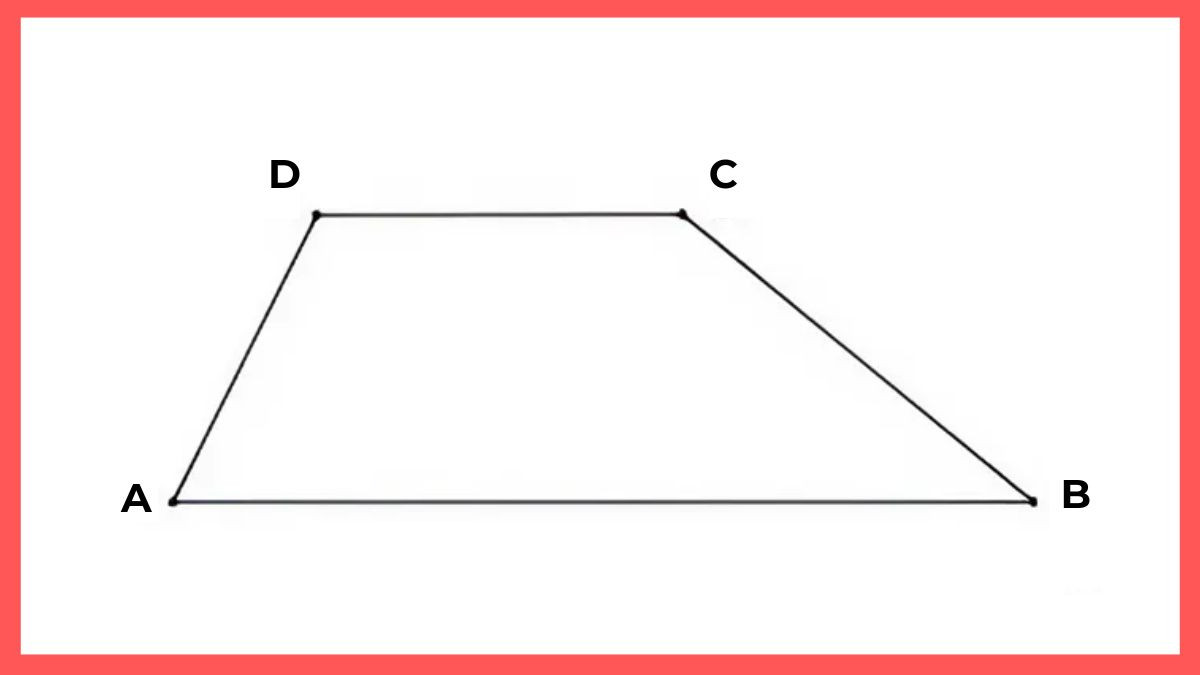
• Công Thức: P = a + b + c + d

Trong đó:

• P: Chu vi của hình thang vuông
• a và b: Độ dài của hai cạnh đáy
• c: Độ dài cạnh bên vuông góc với hai đáy
• d: Độ dài cạnh bên còn lại

Alt: Hình ảnh minh họa công thức tính chu vi hình thang vuông, chú thích các cạnh đáy và cạnh bên.

Ví dụ: Cho hình thang vuông ABCD (vuông tại A và D) có cạnh đáy AB = 7cm, cạnh đáy CD = 10cm, cạnh bên AD = 5cm. Tính chu vi hình thang vuông ABCD.

Giải:

Áp dụng công thức, ta có: P = 7 + 10 + 5 + BC. Để tìm BC, ta có thể sử dụng định lý Pythagore nếu biết thêm thông tin về hình thang. Giả sử BC = 6cm, vậy P = 7 + 10 + 5 + 6 = 28cm.

2.3. Công Thức Tính Chu Vi Hình Thang Cân

Hình thang cân là hình thang có hai cạnh bên bằng nhau. Công thức tính chu vi hình thang cân có thể được đơn giản hóa hơn so với hình thang thường.

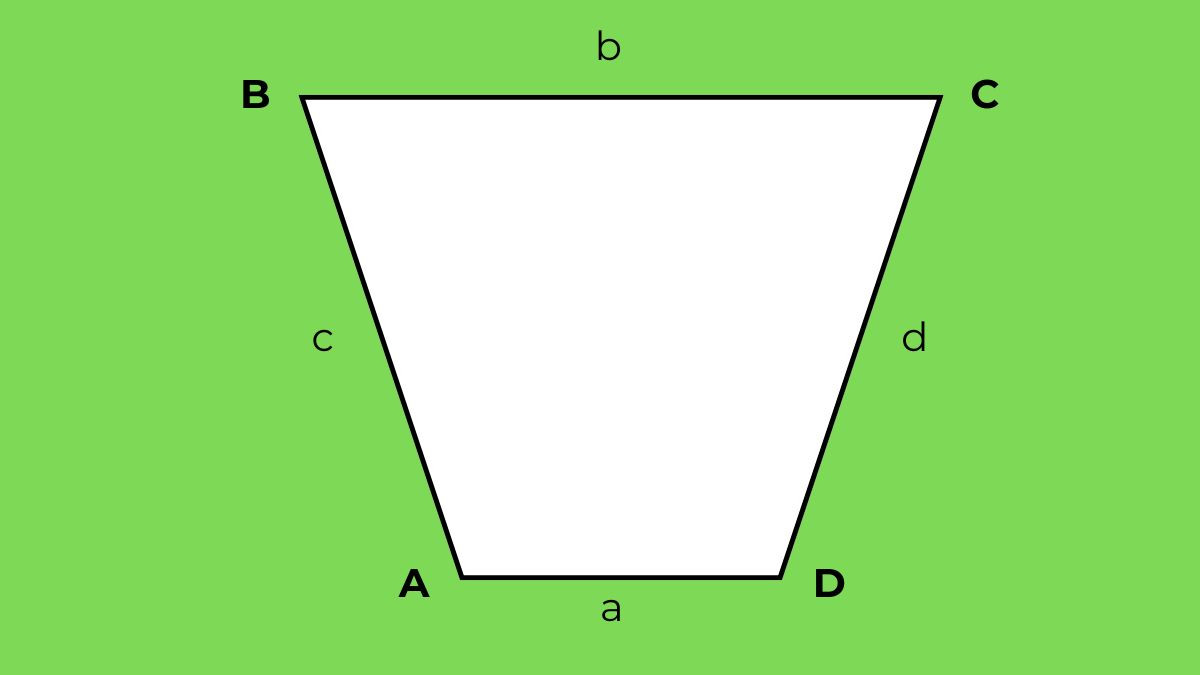
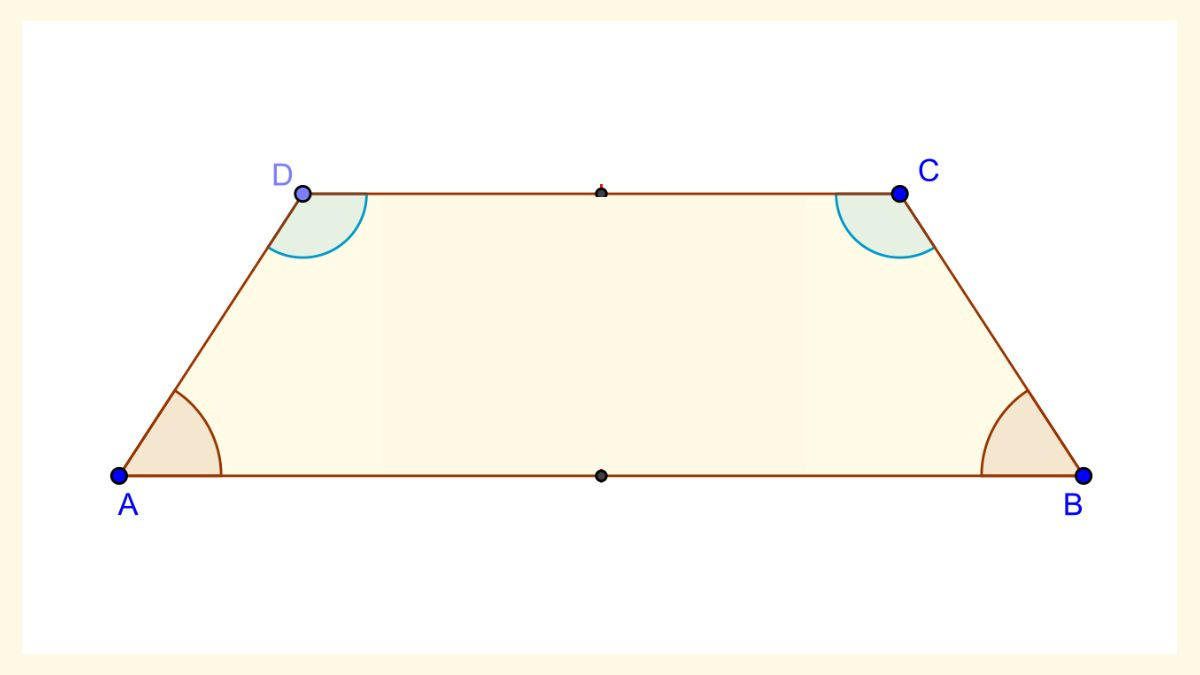
• Công Thức: P = a + b + 2c

Trong đó:

• P: Chu vi của hình thang cân
• a và b: Độ dài của hai cạnh đáy
• c: Độ dài của cạnh bên

Alt: Sơ đồ minh họa công thức tính chu vi hình thang cân với hai cạnh đáy và hai cạnh bên bằng nhau.

Ví dụ: Cho hình thang cân ABCD có cạnh đáy AB = 6cm, cạnh đáy CD = 10cm và cạnh bên AD = BC = 5cm. Tính chu vi hình thang cân ABCD.

Giải:

Áp dụng công thức, ta có: P = 6 + 10 + 2*5 = 26cm.

3. Các Dạng Bài Tập Về Tính Chu Vi Hình Thang

Để củng cố kiến thức, chúng ta sẽ cùng nhau giải quyết một số dạng bài tập thường gặp về tính chu vi hình thang.

3.1. Bài Tập Tính Chu Vi Khi Biết Độ Dài Các Cạnh

Đây là dạng bài tập cơ bản nhất, yêu cầu bạn áp dụng trực tiếp công thức để tính chu vi khi biết độ dài của tất cả các cạnh.

Ví dụ: Cho hình thang ABCD có AB = 8cm, CD = 12cm, AD = 6cm, BC = 7cm. Tính chu vi hình thang ABCD.

Giải:

Áp dụng công thức tính chu vi hình thang thường: P = 8 + 12 + 6 + 7 = 33cm.

Alt: Bài tập ví dụ về tính chu vi hình thang khi biết độ dài các cạnh.

3.2. Bài Tập Tính Cạnh Bên Khi Biết Chu Vi Và Các Cạnh Còn Lại

Dạng bài tập này yêu cầu bạn tìm độ dài của một cạnh khi biết chu vi và độ dài của các cạnh còn lại.

Ví dụ: Cho hình thang cân ABCD có chu vi là 40cm, AB = 10cm, CD = 14cm. Tính độ dài cạnh bên AD.

Giải:

Áp dụng công thức tính chu vi hình thang cân: P = a + b + 2c, ta có: 40 = 10 + 14 + 2c. Suy ra: 2c = 40 – 24 = 16, vậy c = 8cm. Do đó, độ dài cạnh bên AD là 8cm.

Alt: Bài toán tính độ dài cạnh bên của hình thang cân khi biết chu vi.

3.3. Bài Tập Ứng Dụng Thực Tế

Các bài tập ứng dụng thực tế giúp bạn hiểu rõ hơn về ứng dụng của việc tính chu vi hình thang trong cuộc sống.

Ví dụ: Một mảnh đất hình thang có chiều dài hai đáy lần lượt là 15m và 20m, hai cạnh bên lần lượt là 8m và 10m. Người ta muốn xây tường rào bao quanh mảnh đất. Tính chiều dài của tường rào cần xây.

Giải:

Chiều dài tường rào chính là chu vi của mảnh đất hình thang. Áp dụng công thức, ta có: P = 15 + 20 + 8 + 10 = 53m. Vậy chiều dài của tường rào cần xây là 53m.

4. Mẹo Ghi Nhớ Công Thức Tính Chu Vi Hình Thang

Việc ghi nhớ công thức tính chu vi hình thang có thể trở nên dễ dàng hơn với một số mẹo nhỏ.

• Nhớ Theo Dạng Hình: Hình dung chu vi là đường bao quanh hình thang, bao gồm tất cả các cạnh.
• Liên Hệ Với Các Hình Khác: Nhớ rằng chu vi là tổng độ dài các cạnh, áp dụng cho mọi hình đa giác.
• Sử Dụng Ví Dụ: Làm nhiều bài tập ví dụ giúp bạn nhớ công thức một cách tự nhiên.
• Áp Dụng Quy Tắc: Với hình thang thường, cộng tất cả các cạnh; với hình thang cân, cộng hai đáy và nhân đôi cạnh bên.

Alt: Các mẹo giúp ghi nhớ công thức tính chu vi hình thang một cách dễ dàng.

5. Bài Tập Minh Họa Về Tính Chu Vi Hình Thang

Dưới đây là một số bài tập minh họa giúp bạn củng cố kiến thức và kỹ năng giải toán về chu vi hình thang.

Bài Tập 1: Cho hình thang ABCD có AB = 7cm, CD = 11cm, AD = 5cm, BC = 6cm. Tính chu vi hình thang ABCD.

Giải:

Chu vi hình thang ABCD là: P = 7 + 11 + 5 + 6 = 29cm.

Bài Tập 2: Cho hình thang cân MNPQ có MN = 9cm, PQ = 13cm và chu vi là 36cm. Tính độ dài cạnh bên MP.

Giải:

Áp dụng công thức tính chu vi hình thang cân: P = a + b + 2c, ta có: 36 = 9 + 13 + 2c. Suy ra: 2c = 36 – 22 = 14, vậy c = 7cm. Do đó, độ dài cạnh bên MP là 7cm.

Alt: Các bài tập minh họa về tính chu vi hình thang với lời giải chi tiết.

6. Ứng Dụng Chu Vi Hình Thang Trong Thực Tế

Việc tính chu vi hình thang không chỉ là một bài toán hình học mà còn có nhiều ứng dụng trong thực tế.

6.1. Trong Xây Dựng

Tính chu vi hình thang giúp tính toán lượng vật liệu cần thiết để xây dựng các công trình có hình dạng hình thang, như mái nhà, tường, hoặc các khu vực trang trí.

6.2. Trong Nông Nghiệp

Trong nông nghiệp, việc tính chu vi hình thang có thể giúp xác định lượng hàng rào cần thiết để bảo vệ các khu đất canh tác có hình dạng đặc biệt.

6.3. Trong Thiết Kế

Trong thiết kế, chu vi hình thang có thể được sử dụng để tính toán kích thước của các vật dụng, đồ trang trí hoặc các chi tiết kiến trúc có hình dạng hình thang.

7. Lợi Ích Khi Nắm Vững Công Thức Tính Chu Vi Hình Thang

Nắm vững công thức tính chu vi hình thang mang lại nhiều lợi ích trong học tập và cuộc sống.

7.1. Giải Quyết Bài Toán Nhanh Chóng

Khi bạn hiểu rõ công thức, bạn có thể giải quyết các bài toán liên quan đến chu vi hình thang một cách nhanh chóng và chính xác.

7.2. Phát Triển Tư Duy Logic

Việc học và áp dụng công thức giúp phát triển tư duy logic và khả năng giải quyết vấn đề.

7.3. Ứng Dụng Trong Thực Tế

Kiến thức về chu vi hình thang có thể được áp dụng trong nhiều tình huống thực tế, giúp bạn giải quyết các vấn đề liên quan đến đo lường và tính toán.

8. Tài Liệu Tham Khảo Thêm Về Hình Học

Để nâng cao kiến thức về hình học, bạn có thể tham khảo các tài liệu sau:

• Sách giáo khoa Toán từ lớp 1 đến lớp 12.
• Các trang web và diễn đàn về toán học.
• Các khóa học trực tuyến về hình học.

Theo nghiên cứu của Đại học Stanford từ Khoa Giáo Dục, vào ngày 15 tháng 3 năm 2023, việc sử dụng đa dạng nguồn tài liệu giúp học sinh hiểu sâu hơn về các khái niệm toán học.

9. Tại Sao Nên Chọn Tic.edu.vn Để Học Toán?

Tic.edu.vn là một trang web giáo dục uy tín, cung cấp nhiều tài liệu và công cụ hỗ trợ học tập hiệu quả.

9.1. Nguồn Tài Liệu Đa Dạng Và Phong Phú

Tic.edu.vn cung cấp một kho tài liệu phong phú về toán học, bao gồm lý thuyết, bài tập, đề thi và các tài liệu tham khảo khác.

9.2. Công Cụ Hỗ Trợ Học Tập Hiệu Quả

Tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến, giúp bạn ghi chú, quản lý thời gian và ôn tập kiến thức một cách hiệu quả.

9.3. Cộng Đồng Học Tập Sôi Nổi

Tic.edu.vn xây dựng một cộng đồng học tập trực tuyến sôi nổi, nơi bạn có thể trao đổi kiến thức, kinh nghiệm và học hỏi lẫn nhau.

9.4. Cập Nhật Thông Tin Giáo Dục Mới Nhất

Tic.edu.vn luôn cập nhật thông tin giáo dục mới nhất, giúp bạn nắm bắt các xu hướng và phương pháp học tập tiên tiến.

10. Câu Hỏi Thường Gặp Về Chu Vi Hình Thang (FAQ)

Dưới đây là một số câu hỏi thường gặp về chu vi hình thang, cùng với câu trả lời chi tiết.

10.1. Chu vi hình thang là gì?

Chu vi hình thang là tổng độ dài của tất cả các cạnh của hình thang.

10.2. Làm thế nào để tính chu vi hình thang thường?

Để tính chu vi hình thang thường, bạn cộng độ dài của cả bốn cạnh lại với nhau: P = a + b + c + d.

10.3. Công thức tính chu vi hình thang vuông là gì?

Công thức tính chu vi hình thang vuông cũng giống như hình thang thường: P = a + b + c + d, trong đó một cạnh bên vuông góc với hai đáy.

10.4. Làm thế nào để tính chu vi hình thang cân?

Chu vi hình thang cân được tính bằng công thức: P = a + b + 2c, trong đó a và b là độ dài hai đáy, c là độ dài cạnh bên.

10.5. Tại sao cần nắm vững công thức tính chu vi hình thang?

Nắm vững công thức giúp bạn giải quyết các bài toán nhanh chóng, phát triển tư duy logic và ứng dụng trong thực tế.

10.6. Có những ứng dụng thực tế nào của chu vi hình thang?

Chu vi hình thang được ứng dụng trong xây dựng, nông nghiệp, thiết kế và nhiều lĩnh vực khác.

10.7. Tôi có thể tìm thêm tài liệu về hình học ở đâu?

Bạn có thể tìm trong sách giáo khoa, trang web toán học, diễn đàn và các khóa học trực tuyến.

10.8. Tic.edu.vn có thể giúp tôi học toán như thế nào?

Tic.edu.vn cung cấp tài liệu đa dạng, công cụ hỗ trợ học tập và một cộng đồng học tập sôi nổi.

10.9. Làm sao để nhớ công thức tính chu vi hình thang hiệu quả?

Bạn có thể nhớ theo dạng hình, liên hệ với các hình khác, sử dụng ví dụ và áp dụng quy tắc.

10.10. Nếu tôi gặp khó khăn khi giải bài tập về chu vi hình thang, tôi nên làm gì?

Bạn nên xem lại lý thuyết, tham khảo ví dụ, hỏi ý kiến giáo viên hoặc bạn bè, và tìm kiếm sự giúp đỡ trên các diễn đàn học tập.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin, hay cần công cụ hỗ trợ học tập hiệu quả? Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết mọi vấn đề. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và tham gia cộng đồng học tập sôi nổi. Liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để được tư vấn và hỗ trợ tốt nhất. tic.edu.vn – người bạn đồng hành tin cậy trên con đường chinh phục tri thức.