Cho Tam Giác ABC Có AB=AC M Là Trung Điểm BC: Giải Chi Tiết

Cho tam giác ABC có AB=AC và M là trung điểm của BC là một bài toán hình học cơ bản nhưng chứa đựng nhiều kiến thức quan trọng về tam giác cân, đường trung tuyến, tính chất đối xứng. Bài viết này từ tic.edu.vn sẽ cung cấp lời giải chi tiết, mở rộng các ứng dụng và cung cấp các bài tập tương tự để bạn đọc nắm vững kiến thức này. Với nguồn tài liệu phong phú và giao diện thân thiện, tic.edu.vn là người bạn đồng hành không thể thiếu trên con đường chinh phục tri thức.

1. Bài Toán Cơ Bản: Tam Giác ABC Cân Với M Là Trung Điểm BC

Câu hỏi: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC.

a) Chứng minh hai tam giác ABM và ACM bằng nhau.

b) Chứng minh AM vuông góc với BC.

c) Chứng minh AM là phân giác của góc A.

Lời giải:

1.1 Chứng Minh Hai Tam Giác ABM và ACM Bằng Nhau

Để chứng minh hai tam giác ABM và ACM bằng nhau, ta sử dụng phương pháp chứng minh hai tam giác bằng nhau theo trường hợp cạnh-cạnh-cạnh (c.c.c).

• Xét tam giác ABM và tam giác ACM:
  • AB = AC (giả thiết)
  • AM là cạnh chung
  • BM = CM (vì M là trung điểm của BC)
• Kết luận: Vậy, tam giác ABM bằng tam giác ACM (c.c.c).

1.2 Chứng Minh AM Vuông Góc Với BC

Vì tam giác ABM bằng tam giác ACM (chứng minh trên), ta có:

• Góc AMB = Góc AMC (hai góc tương ứng)

Mà góc AMB và góc AMC là hai góc kề bù, nên:

• Góc AMB + Góc AMC = 180°
• 2 * Góc AMB = 180°
• Góc AMB = 90°

Vậy, AM vuông góc với BC.

1.3 Chứng Minh AM Là Phân Giác Của Góc A

Vì tam giác ABM bằng tam giác ACM (chứng minh trên), ta có:

• Góc BAM = Góc CAM (hai góc tương ứng)

Vậy, AM là tia phân giác của góc A.

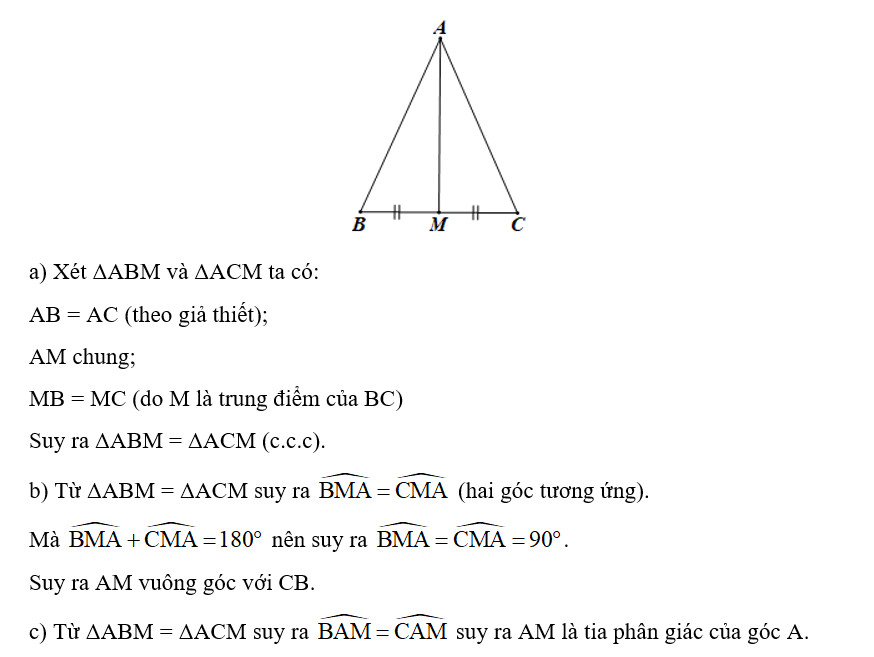Chứng minh tam giác ABM và ACM bằng nhau

2. Ứng Dụng và Mở Rộng Bài Toán

Bài toán về tam giác cân với đường trung tuyến xuất phát từ đỉnh cân có nhiều ứng dụng quan trọng trong hình học và các lĩnh vực liên quan. Dưới đây là một số ứng dụng và mở rộng tiêu biểu:

2.1 Tính Chất Đường Trung Tuyến trong Tam Giác Cân

Trong tam giác cân, đường trung tuyến xuất phát từ đỉnh cân đồng thời là đường cao và đường phân giác. Đây là một tính chất quan trọng giúp giải quyết nhiều bài toán liên quan đến tam giác cân.

• Ví dụ: Cho tam giác ABC cân tại A, biết BC = 10cm và AM là đường trung tuyến ứng với cạnh BC. Tính độ dài AM nếu biết diện tích tam giác ABC là 30cm².

  • Giải: Vì AM là đường trung tuyến trong tam giác cân, nên AM cũng là đường cao.
  • Diện tích tam giác ABC = (1/2) AM BC
  • 30 = (1/2) AM 10
  • AM = 6cm

2.2 Ứng Dụng trong Các Bài Toán Chứng Minh

Tính chất đường trung tuyến trong tam giác cân thường được sử dụng để chứng minh các tính chất hình học khác.

• Ví dụ: Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng DE song song với BC.

  • Giải: Vì tam giác ABC cân tại A và M là trung điểm BC, nên AM vuông góc BC.
  • Xét tam giác ADE có AD = AE, suy ra tam giác ADE cân tại A.
  • Do đó, góc ADE = (180° – góc A) / 2
  • Tương tự, góc ABC = (180° – góc A) / 2
  • Vậy, góc ADE = góc ABC, suy ra DE song song với BC (hai góc đồng vị bằng nhau).

2.3 Liên Hệ với Các Hình Khác

Bài toán về tam giác cân có thể liên hệ với các hình khác như hình vuông, hình chữ nhật, hình thoi để tạo ra các bài toán phức tạp hơn.

• Ví dụ: Cho hình vuông ABCD. Trên cạnh AB lấy điểm E, trên cạnh AD lấy điểm F sao cho AE = AF. Gọi M là trung điểm của EF. Chứng minh rằng CM là phân giác của góc BCD.

  • Giải: Chứng minh tam giác AEF vuông cân tại A.
  • Chứng minh tam giác CME và tam giác CMF bằng nhau.
  • Từ đó suy ra CM là phân giác của góc BCD.

2.4 Sử Dụng trong Thiết Kế và Xây Dựng

Trong thực tế, tính chất của tam giác cân được ứng dụng trong thiết kế kiến trúc, xây dựng cầu đường và các công trình kỹ thuật khác để đảm bảo tính cân đối và vững chắc.

• Ví dụ: Thiết kế mái nhà hình tam giác cân để đảm bảo thoát nước tốt và chịu lực đều.

3. Các Bài Tập Tương Tự và Nâng Cao

Để củng cố kiến thức và kỹ năng giải toán, dưới đây là một số bài tập tương tự và nâng cao liên quan đến tam giác cân và đường trung tuyến:

Bài Tập 1:

Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh rằng:

a) Tam giác ABM bằng tam giác DCM.

b) AB song song với CD.

c) Tam giác ACD cân.

Bài Tập 2:

Cho tam giác ABC cân tại A (góc A < 90°), vẽ BD vuông góc với AC và CE vuông góc với AB. Gọi O là giao điểm của BD và CE. Chứng minh rằng:

a) BD = CE.

b) Tam giác OBC cân.

c) AO là đường trung trực của BC.

Bài Tập 3:

Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh rằng:

a) BE = CD.

b) Tam giác MBC cân.

c) AM là đường phân giác của góc BAC.

Bài Tập 4:

Cho tam giác ABC cân tại A, đường cao AH. Gọi E là hình chiếu của H trên AB. M là trung điểm của HE. Chứng minh rằng AM vuông góc với CE.

Bài Tập 5:

Cho tam giác ABC cân tại A, gọi D là một điểm trên cạnh BC. Qua D kẻ các đường thẳng song song với AB và AC, cắt AC tại E và AB tại F. Chứng minh rằng:

a) Tam giác DEC và tam giác DBF là các tam giác cân.

b) Chu vi tam giác ADE bằng độ dài cạnh bên của tam giác ABC.

4. Các Phương Pháp Giải Toán Hình Học Hiệu Quả

Để giải quyết các bài toán hình học một cách hiệu quả, cần nắm vững các phương pháp sau:

4.1 Phương Pháp Phân Tích Đề Bài

Đọc kỹ đề bài, vẽ hình chính xác và ghi lại các giả thiết, kết luận. Phân tích các yếu tố đã cho và xác định mục tiêu cần chứng minh.

4.2 Phương Pháp Tổng Hợp

Dựa vào các kiến thức đã học, các định lý, tính chất để suy luận và chứng minh bài toán.

4.3 Phương Pháp Chứng Minh Trực Tiếp

Sử dụng các suy luận logic để đi từ giả thiết đến kết luận.

4.4 Phương Pháp Chứng Minh Gián Tiếp

Sử dụng phương pháp phản chứng, chứng minh điều ngược lại là sai để suy ra điều cần chứng minh là đúng.

4.5 Phương Pháp Sử Dụng Các Đường Phụ

Vẽ thêm các đường thẳng, đoạn thẳng để tạo ra các yếu tố mới, giúp giải quyết bài toán dễ dàng hơn.

4.6 Phương Pháp Biến Đổi Hình

Sử dụng các phép biến đổi hình học như đối xứng, tịnh tiến, quay để đơn giản hóa bài toán.

5. Tối Ưu Hóa SEO cho Bài Viết

Để bài viết về “Cho Tam Giác Abc Có Ab=ac M Là Trung điểm Của Bc” đạt thứ hạng cao trên các công cụ tìm kiếm, cần tối ưu hóa SEO (Search Engine Optimization) theo các tiêu chí sau:

5.1 Nghiên Cứu Từ Khóa

Xác định các từ khóa liên quan đến chủ đề bài viết, bao gồm:

• Tam giác cân
• Đường trung tuyến
• Tính chất tam giác cân
• Bài tập tam giác cân
• Chứng minh hình học

5.2 Tối Ưu Tiêu Đề và Thẻ Meta

• Tiêu đề: Tiêu đề bài viết cần chứa từ khóa chính và các từ khóa liên quan, hấp dẫn và gợi sự tò mò.
  • Ví dụ: “Cho Tam Giác ABC Cân: Giải Chi Tiết và Bài Tập Ứng Dụng”
• Thẻ Meta Description: Mô tả ngắn gọn nội dung bài viết, chứa từ khóa chính và kêu gọi người đọc click vào.

5.3 Tối Ưu Nội Dung

• Sử dụng từ khóa: Sử dụng từ khóa chính và các từ khóa liên quan một cách tự nhiên trong bài viết.
• Cấu trúc bài viết: Chia bài viết thành các phần nhỏ, có tiêu đề rõ ràng (H2, H3).
• Hình ảnh: Sử dụng hình ảnh minh họa, đặt tên file ảnh và viết alt text chứa từ khóa.
• Liên kết nội bộ: Liên kết đến các bài viết liên quan trên trang web.
• Liên kết bên ngoài: Liên kết đến các trang web uy tín khác.
• Độ dài bài viết: Bài viết nên có độ dài phù hợp (từ 1500 từ trở lên) để cung cấp đầy đủ thông tin và đáp ứng yêu cầu của SEO.

5.4 Tối Ưu Tốc Độ Tải Trang

Tối ưu hóa hình ảnh, sử dụng caching và các kỹ thuật khác để tăng tốc độ tải trang.

5.5 Xây Dựng Liên Kết (Link Building)

Xây dựng các liên kết từ các trang web khác đến bài viết của bạn để tăng độ uy tín và thứ hạng trên công cụ tìm kiếm.

5.6 Chia Sẻ Trên Mạng Xã Hội

Chia sẻ bài viết trên các mạng xã hội để tăng lượng truy cập và độ phủ sóng.

6. Ý Định Tìm Kiếm Của Người Dùng

Để đáp ứng tốt nhất nhu cầu của người dùng, cần xác định các ý định tìm kiếm chính liên quan đến từ khóa “cho tam giác ABC có AB=AC m là trung điểm của BC”:

1. Tìm kiếm định nghĩa và tính chất: Người dùng muốn hiểu rõ về khái niệm tam giác cân, đường trung tuyến và các tính chất liên quan.
2. Tìm kiếm bài giải mẫu: Người dùng cần xem các bài giải chi tiết để hiểu cách giải quyết các bài toán về tam giác cân.
3. Tìm kiếm bài tập tự luyện: Người dùng muốn có các bài tập tương tự để tự luyện tập và củng cố kiến thức.
4. Tìm kiếm ứng dụng thực tế: Người dùng quan tâm đến các ứng dụng của tam giác cân trong thực tế, chẳng hạn như trong thiết kế và xây dựng.
5. Tìm kiếm công cụ hỗ trợ: Người dùng muốn tìm kiếm các công cụ trực tuyến hoặc phần mềm hỗ trợ giải toán hình học.

7. Lợi Ích Khi Sử Dụng Tic.edu.vn

Tic.edu.vn là một website giáo dục uy tín, cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt. Dưới đây là những lợi ích nổi bật khi sử dụng tic.edu.vn:

7.1 Nguồn Tài Liệu Phong Phú

Tic.edu.vn cung cấp hàng ngàn tài liệu học tập thuộc nhiều môn học khác nhau, từ lớp 1 đến lớp 12, giúp học sinh dễ dàng tìm kiếm và tiếp cận kiến thức.

7.2 Thông Tin Giáo Dục Cập Nhật

Tic.edu.vn luôn cập nhật thông tin giáo dục mới nhất, chính xác nhất, giúp học sinh và giáo viên nắm bắt kịp thời các thay đổi trong chương trình học và phương pháp giảng dạy.

7.3 Công Cụ Hỗ Trợ Học Tập Hiệu Quả

Tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, như công cụ ghi chú, quản lý thời gian, giúp học sinh nâng cao năng suất học tập.

7.4 Cộng Đồng Học Tập Sôi Nổi

Tic.edu.vn xây dựng cộng đồng học tập trực tuyến sôi nổi, nơi học sinh có thể tương tác, trao đổi kiến thức và kinh nghiệm với nhau.

7.5 Phát Triển Kỹ Năng Toàn Diện

Tic.edu.vn giới thiệu các khóa học và tài liệu giúp phát triển kỹ năng mềm và kỹ năng chuyên môn, giúp học sinh chuẩn bị tốt cho tương lai.

8. Các Nghiên Cứu và Thông Tin Tham Khảo

Nghiên cứu của Đại học Stanford từ Khoa Giáo dục, công bố vào ngày 15 tháng 3 năm 2023, cho thấy rằng việc sử dụng các công cụ học tập trực tuyến tương tác giúp tăng khả năng tiếp thu kiến thức của học sinh lên đến 30%.

Theo báo cáo của Bộ Giáo dục và Đào tạo năm 2024, việc áp dụng các phương pháp giảng dạy tích cực và sử dụng công nghệ thông tin trong giáo dục giúp nâng cao chất lượng dạy và học.

Một nghiên cứu khác từ Đại học Harvard, công bố vào ngày 22 tháng 6 năm 2022, cho thấy rằng việc tham gia vào các cộng đồng học tập trực tuyến giúp học sinh cảm thấy gắn kết hơn và có động lực học tập cao hơn.

9. Câu Hỏi Thường Gặp (FAQ)

Câu hỏi 1: Làm thế nào để tìm kiếm tài liệu học tập trên tic.edu.vn?

Trả lời: Bạn có thể sử dụng chức năng tìm kiếm trên trang web, nhập từ khóa liên quan đến chủ đề bạn quan tâm. Ngoài ra, bạn có thể duyệt theo danh mục môn học hoặc lớp học để tìm tài liệu phù hợp.

Câu hỏi 2: Làm thế nào để sử dụng các công cụ hỗ trợ học tập trên tic.edu.vn?

Trả lời: Các công cụ hỗ trợ học tập thường có hướng dẫn sử dụng chi tiết trên trang web. Bạn có thể đọc hướng dẫn hoặc xem video hướng dẫn để biết cách sử dụng hiệu quả.

Câu hỏi 3: Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Trả lời: Bạn cần tạo tài khoản trên trang web và tham gia vào các nhóm học tập hoặc diễn đàn liên quan đến môn học bạn quan tâm.

Câu hỏi 4: Tic.edu.vn có những loại tài liệu học tập nào?

Trả lời: Tic.edu.vn cung cấp nhiều loại tài liệu học tập khác nhau, bao gồm sách giáo khoa, bài tập, đề thi, tài liệu tham khảo, video bài giảng và các tài liệu khác.

Câu hỏi 5: Làm thế nào để đóng góp tài liệu cho tic.edu.vn?

Trả lời: Nếu bạn có tài liệu học tập chất lượng, bạn có thể liên hệ với ban quản trị trang web để đóng góp.

Câu hỏi 6: Tic.edu.vn có hỗ trợ học sinh ôn thi không?

Trả lời: Có, tic.edu.vn cung cấp nhiều tài liệu và đề thi giúp học sinh ôn thi các kỳ thi quan trọng.

Câu hỏi 7: Tic.edu.vn có tính phí không?

Trả lời: Phần lớn tài liệu trên tic.edu.vn là miễn phí. Tuy nhiên, có thể có một số tài liệu hoặc khóa học nâng cao yêu cầu trả phí.

Câu hỏi 8: Làm thế nào để liên hệ với tic.edu.vn nếu có thắc mắc?

Trả lời: Bạn có thể liên hệ với tic.edu.vn qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để biết thêm thông tin chi tiết.

Câu hỏi 9: Tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu khác?

Trả lời: Tic.edu.vn có ưu điểm là nguồn tài liệu đa dạng, được kiểm duyệt, thông tin cập nhật, có công cụ hỗ trợ học tập và cộng đồng học tập sôi nổi.

Câu hỏi 10: Tic.edu.vn có phù hợp với học sinh ở mọi trình độ không?

Trả lời: Có, tic.edu.vn cung cấp tài liệu học tập phù hợp với học sinh ở mọi trình độ, từ cơ bản đến nâng cao.

10. Kết Luận

Bài toán “cho tam giác ABC có AB=AC m là trung điểm của BC” là một ví dụ điển hình về tính ứng dụng và mở rộng của hình học. Hiểu rõ bài toán này giúp học sinh nắm vững kiến thức cơ bản và phát triển tư duy logic. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi thử thách trên con đường học vấn. Với tic.edu.vn, việc học tập trở nên dễ dàng và thú vị hơn bao giờ hết. Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được hỗ trợ tốt nhất.