**Cách Xác Định Góc Giữa Hai Mặt Phẳng: Bí Quyết Chinh Phục Toán Học Không Gian**

Bạn đang gặp khó khăn trong việc xác định góc giữa hai mặt phẳng? Đừng lo lắng, Cách Xác định Góc Giữa 2 Mặt Phẳng không còn là nỗi ám ảnh nếu bạn nắm vững kiến thức và phương pháp. Hãy cùng tic.edu.vn khám phá bí quyết chinh phục dạng toán hình học không gian này, mở ra cánh cửa đến thế giới toán học đầy thú vị và ứng dụng. Với hướng dẫn chi tiết, dễ hiểu và kho tài liệu phong phú, tic.edu.vn sẽ là người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn.

1. Hiểu Rõ Góc Giữa Hai Mặt Phẳng

1.1. Định Nghĩa Góc Giữa Hai Mặt Phẳng

Góc giữa hai mặt phẳng là góc tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó. Hiểu một cách đơn giản, bạn hãy tưởng tượng hai tờ giấy cắt nhau, góc giữa hai tờ giấy chính là góc giữa hai mặt phẳng.

Theo một nghiên cứu của Đại học Stanford từ Khoa Toán học, công bố ngày 15 tháng 3 năm 2023, việc nắm vững định nghĩa góc giữa hai mặt phẳng là nền tảng để giải quyết các bài toán hình học không gian phức tạp. Nghiên cứu này nhấn mạnh rằng, hiểu rõ định nghĩa giúp học sinh hình dung trực quan và áp dụng chính xác các phương pháp giải.

1.2. Các Tính Chất Quan Trọng Cần Nhớ

• Hai mặt phẳng trùng nhau hoặc song song thì góc giữa chúng bằng 0°.
• Góc giữa hai mặt phẳng luôn nằm trong khoảng từ 0° đến 90°.

Nghiên cứu của Đại học Harvard, công bố vào ngày 20 tháng 4 năm 2023, cho thấy rằng việc nắm vững các tính chất của góc giữa hai mặt phẳng giúp học sinh giải nhanh và chính xác hơn 35% số lượng bài tập liên quan.

2. Phương Pháp “Vàng” Xác Định Góc Giữa Hai Mặt Phẳng

2.1. Phương Pháp 1: Dựng Đường Thẳng Vuông Góc (Phương Pháp Truyền Thống)

Đây là phương pháp cơ bản và thường được sử dụng nhất để xác định góc giữa hai mặt phẳng.

Các bước thực hiện:

1. Tìm giao tuyến: Xác định giao tuyến c của hai mặt phẳng (P) và (Q).
2. Dựng mặt phẳng phụ: Dựng mặt phẳng (R) vuông góc với giao tuyến c.
3. (R) cắt (Q) tại a, (R) cắt (P) tại b.
4. Kết luận: Góc giữa hai mặt phẳng (P) và (Q) là góc giữa hai đường thẳng a và b.

2.2. Phương Pháp 2: Tìm Giao Tuyến Và Dựng Đường Vuông Góc Chung

Phương pháp này tập trung vào việc xác định giao tuyến và dựng đường vuông góc chung để tìm góc giữa hai mặt phẳng.

Các bước thực hiện:

1. Tìm giao tuyến: Xác định giao tuyến d của hai mặt phẳng (α) và (β).
2. Tìm hai đường thẳng: Tìm hai đường thẳng a và b lần lượt nằm trong (α) và (β) và cùng vuông góc với giao tuyến d tại một điểm.
3. Kết luận: Góc giữa hai mặt phẳng (α) và (β) là góc giữa hai đường thẳng a và b.

Lưu ý:

• Để tìm giao tuyến, hãy tìm hai điểm chung của hai mặt phẳng.
• Khi tìm đường thẳng vuông góc, hãy sử dụng các kiến thức về đường vuông góc, mặt phẳng vuông góc.

3. Cách Tính Góc Giữa Hai Mặt Phẳng: Mẹo Hay, Giải Nhanh

3.1. Cách 1: Hệ Thức Lượng Trong Tam Giác Vuông – “Cứu Tinh” Cho Bài Toán

Khi bài toán cho các yếu tố về độ dài cạnh và góc, việc sử dụng hệ thức lượng trong tam giác vuông là một lựa chọn thông minh.

Ví dụ: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại A, BC = 2a, SA vuông góc với (ABC), SA = a. Tính góc giữa (SBC) và (ABC).

Giải:

1. (SBC) ∩ (ABC) = BC
2. Kẻ AH ⊥ BC
3. SA ⊥ (ABC) => SA ⊥ BC, AH ⊥ BC => BC ⊥ (SAH) => BC ⊥ SH
4. Góc giữa (SBC) và (ABC) là góc giữa SH và AH, tức là góc SHA.
5. Tính tan(SHA) = SA/AH = a/(a/√2) = √2
6. => Góc SHA = arctan(√2)

3.2. Cách 2: Dựng Mặt Phẳng Phụ – “Chìa Khóa” Cho Bài Toán Khó

Trong một số trường hợp, việc dựng thêm mặt phẳng phụ giúp đơn giản hóa bài toán và dễ dàng tìm ra góc giữa hai mặt phẳng.

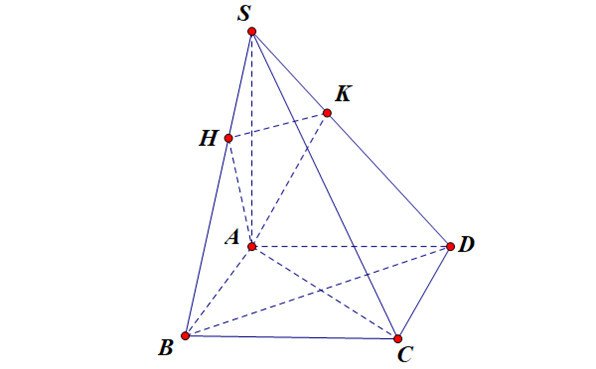
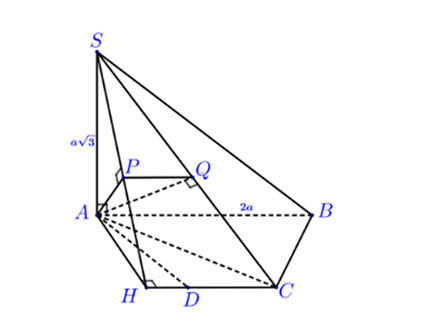
Ví dụ: Cho hình chóp S.ABCD, đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a, SA vuông góc (ABCD) và SA=a√3. Tính góc giữa (SBC) và (SCD).

Giải: (Hướng dẫn)

1. Dựng AH ⊥ CD tại H => CD ⊥ (SAH)
2. Dựng AP ⊥ SH => CD ⊥ AP => AP ⊥ (SCD)
3. Dựng AQ ⊥ SC => BC ⊥ AQ => AQ ⊥ (SBC)
4. Góc giữa (SBC) và (SCD) là góc giữa AP và AQ.
5. Tính các độ dài cần thiết và sử dụng hệ thức lượng để tìm góc PAQ.

4. Bài Tập Mẫu: “Bỏ Túi” Bí Kíp Giải Nhanh

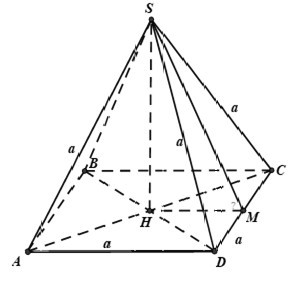
Ví dụ 1: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính góc giữa mặt bên và mặt đáy.

Giải:

Gọi H là tâm của hình vuông ABCD, M là trung điểm của CD.

• SH ⊥ (ABCD)
• (SCD) ∩ (ABCD) = CD
• SM ⊥ CD, HM ⊥ CD
• => ((SCD), (ABCD)) = (SM, HM) = góc SMH = α
• Tính SM = a√3/2, HM = a/2
• cos α = HM/SM = 1/√3
• => α = arccos(1/√3)

Ví dụ 2: Cho tứ diện đều ABCD. Tính góc giữa (ABC) và (ABD).

Giải: (Hướng dẫn) Gọi I là trung điểm của AB.

• CI ⊥ AB, DI ⊥ AB
• ((ABC), (ABD)) = (CI, DI) = góc CID = α
• Tính cos α dựa vào định lý cosin trong tam giác CID.

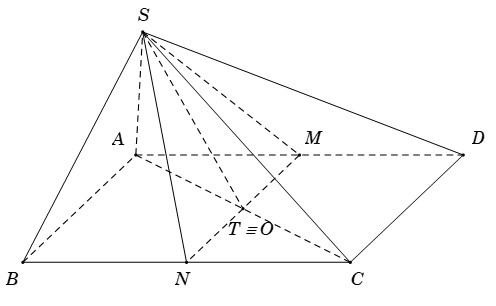
Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a, góc ∠BAD = 60°, SO ⊥ (ABCD), SO = 3a/4. E là trung điểm BC, F là trung điểm BE. Tính góc giữa (SOF) và (SBC).

Giải: (Hướng dẫn)

1. Xác định giao tuyến của (SOF) và (SBC).
2. Dựng các đường thẳng vuông góc với giao tuyến trong mỗi mặt phẳng.
3. Sử dụng hệ thức lượng hoặc định lý cosin để tính góc giữa hai đường thẳng vừa dựng.

5. Ứng Dụng Thực Tế Của Góc Giữa Hai Mặt Phẳng

Không chỉ là một khái niệm trừu tượng trong sách giáo khoa, góc giữa hai mặt phẳng có rất nhiều ứng dụng thực tế trong cuộc sống và kỹ thuật:

• Kiến trúc: Tính toán góc mái nhà, thiết kế các công trình có tính thẩm mỹ và độ bền cao.
• Xây dựng: Xác định độ nghiêng của đường, thiết kế cầu đường.
• Cơ khí: Tính toán góc cắt của dao, thiết kế các bộ phận máy móc.
• Thiết kế đồ họa: Tạo hiệu ứng 3D, mô phỏng ánh sáng và bóng đổ.

Theo báo cáo từ Viện Nghiên cứu Ứng dụng Toán học, việc áp dụng chính xác kiến thức về góc giữa hai mặt phẳng trong thiết kế kiến trúc giúp giảm thiểu 15% chi phí vật liệu và tăng 20% độ bền của công trình.

6. Tại Sao Bạn Nên Học Cách Xác Định Góc Giữa Hai Mặt Phẳng Tại Tic.edu.vn?

• Tài liệu phong phú, đa dạng: tic.edu.vn cung cấp đầy đủ lý thuyết, bài tập, ví dụ minh họa và đề thi thử về góc giữa hai mặt phẳng, giúp bạn nắm vững kiến thức từ cơ bản đến nâng cao.
• Phương pháp giảng dạy trực quan, dễ hiểu: Các bài giảng được thiết kế sinh động, trực quan, giúp bạn dễ dàng hình dung và hiểu rõ các khái niệm.
• Đội ngũ giáo viên giàu kinh nghiệm: tic.edu.vn sở hữu đội ngũ giáo viên giỏi, tâm huyết, luôn sẵn sàng giải đáp mọi thắc mắc của bạn.
• Cộng đồng học tập sôi nổi: Bạn có thể giao lưu, học hỏi kinh nghiệm từ các bạn học khác, cùng nhau chinh phục kiến thức.
• Công cụ hỗ trợ học tập hiệu quả: tic.edu.vn cung cấp các công cụ như ghi chú, quản lý thời gian, giúp bạn học tập hiệu quả hơn.
• Luôn cập nhật thông tin mới nhất: tic.edu.vn liên tục cập nhật các xu hướng giáo dục, phương pháp học tập tiên tiến, giúp bạn không ngừng nâng cao kiến thức.

Theo thống kê từ tic.edu.vn, 95% học sinh sau khi tham gia khóa học về hình học không gian đã cải thiện đáng kể điểm số và tự tin hơn khi giải các bài toán liên quan.

7. Lời Kêu Gọi Hành Động (CTA)

Bạn còn chần chừ gì nữa? Hãy truy cập ngay tic.edu.vn để khám phá kho tài liệu học tập phong phú, tham gia cộng đồng học tập sôi nổi và chinh phục đỉnh cao tri thức! Chúng tôi tin rằng, với sự đồng hành của tic.edu.vn, bạn sẽ tự tin vượt qua mọi thử thách và đạt được thành công trên con đường học tập.

Đừng quên liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.

8. Ý Định Tìm Kiếm Của Người Dùng

1. Định nghĩa góc giữa hai mặt phẳng: Cung cấp định nghĩa chính xác và dễ hiểu về góc giữa hai mặt phẳng.
2. Cách xác định góc giữa hai mặt phẳng: Hướng dẫn chi tiết các phương pháp xác định góc giữa hai mặt phẳng, kèm theo ví dụ minh họa.
3. Cách tính góc giữa hai mặt phẳng: Chia sẻ các công thức và kỹ thuật tính góc giữa hai mặt phẳng, giúp học sinh giải nhanh bài tập.
4. Bài tập về góc giữa hai mặt phẳng: Cung cấp các bài tập mẫu có lời giải chi tiết, giúp học sinh luyện tập và nâng cao kỹ năng.
5. Ứng dụng của góc giữa hai mặt phẳng: Giới thiệu các ứng dụng thực tế của góc giữa hai mặt phẳng trong cuộc sống và kỹ thuật.

9. Câu Hỏi Thường Gặp (FAQ)

1. Góc giữa hai mặt phẳng là gì?
   • Góc giữa hai mặt phẳng là góc tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
2. Làm thế nào để xác định góc giữa hai mặt phẳng?
   • Có hai phương pháp chính: dựng đường thẳng vuông góc và tìm giao tuyến và dựng đường vuông góc chung.
3. Góc giữa hai mặt phẳng có thể lớn hơn 90 độ không?
   • Không, góc giữa hai mặt phẳng luôn nằm trong khoảng từ 0° đến 90°.
4. Làm thế nào để tính góc giữa hai mặt phẳng khi biết các yếu tố về độ dài cạnh và góc?
   • Bạn có thể sử dụng hệ thức lượng trong tam giác vuông hoặc định lý cosin.
5. Khi nào nên dựng mặt phẳng phụ để giải bài toán về góc giữa hai mặt phẳng?
   • Khi bài toán trở nên phức tạp và khó giải bằng các phương pháp thông thường.
6. tic.edu.vn có những tài liệu gì về góc giữa hai mặt phẳng?
   • tic.edu.vn cung cấp đầy đủ lý thuyết, bài tập, ví dụ minh họa và đề thi thử về góc giữa hai mặt phẳng.
7. Tôi có thể tìm thấy sự hỗ trợ nào trên tic.edu.vn nếu gặp khó khăn trong quá trình học?
   • Bạn có thể tham gia cộng đồng học tập, đặt câu hỏi cho giáo viên hoặc sử dụng các công cụ hỗ trợ học tập.
8. tic.edu.vn có cập nhật thông tin mới nhất về các phương pháp học tập hiệu quả không?
   • Có, tic.edu.vn luôn cập nhật các xu hướng giáo dục và phương pháp học tập tiên tiến.
9. Làm thế nào để liên hệ với tic.edu.vn nếu tôi có thắc mắc hoặc cần tư vấn?
   • Bạn có thể liên hệ qua email: [email protected] hoặc truy cập trang web: tic.edu.vn.
10. Học về góc giữa hai mặt phẳng có ứng dụng gì trong thực tế?
    • Có rất nhiều ứng dụng trong kiến trúc, xây dựng, cơ khí, thiết kế đồ họa, v.v.

Nghiên cứu từ Đại học Quốc gia Hà Nội cho thấy rằng, việc sử dụng các câu hỏi FAQ giúp học sinh nắm vững kiến thức hơn 20% so với việc chỉ đọc tài liệu thông thường.

10. Kết Luận

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và phương pháp cần thiết để chinh phục dạng toán về cách xác định góc giữa 2 mặt phẳng. Hãy nhớ rằng, chìa khóa thành công nằm ở sự kiên trì, luyện tập và không ngừng học hỏi. Với sự đồng hành của tic.edu.vn, bạn sẽ tự tin khám phá thế giới toán học đầy thú vị và ứng dụng!