Bạn đang tìm hiểu về Cách Tính Xác Suất Thực Nghiệm? Bạn muốn nắm vững kiến thức và ứng dụng nó vào thực tế? Hãy cùng tic.edu.vn khám phá bí mật của xác suất thực nghiệm qua bài viết chi tiết này, nơi bạn sẽ tìm thấy định nghĩa, công thức, ví dụ minh họa, bài tập áp dụng và những ứng dụng thú vị của nó trong cuộc sống. Chúng tôi cung cấp giải pháp toàn diện để bạn chinh phục khái niệm này một cách dễ dàng và hiệu quả.
Contents
- 1. Xác Suất Thực Nghiệm Là Gì?
- 1.1. Định Nghĩa Chi Tiết Về Xác Suất Thực Nghiệm
- 1.2. Phân Biệt Xác Suất Thực Nghiệm Và Xác Suất Lý Thuyết
- 1.3. Tại Sao Xác Suất Thực Nghiệm Quan Trọng?
- 2. Công Thức Tính Xác Suất Thực Nghiệm
- 2.1. Giải Thích Các Thành Phần Trong Công Thức
- 2.2. Ví Dụ Minh Họa Cách Áp Dụng Công Thức
- 2.3. Lưu Ý Khi Sử Dụng Công Thức
- 3. Các Bước Tính Xác Suất Thực Nghiệm
- 3.1. Bước 1: Xác Định Sự Kiện Cần Tính Xác Suất
- 3.2. Bước 2: Thực Hiện Thử Nghiệm Nhiều Lần
- 3.3. Bước 3: Đếm Số Lần Sự Kiện Xảy Ra
- 3.4. Bước 4: Áp Dụng Công Thức Tính Xác Suất Thực Nghiệm
- 3.5. Bước 5: Phân Tích Và Đánh Giá Kết Quả
- 4. Các Yếu Tố Ảnh Hưởng Đến Xác Suất Thực Nghiệm
- 4.1. Số Lượng Thử Nghiệm
- 4.2. Tính Ngẫu Nhiên Của Thử Nghiệm
- 4.3. Điều Kiện Thử Nghiệm
- 4.4. Sai Số
- 5. Ứng Dụng Của Xác Suất Thực Nghiệm Trong Thực Tế
- 5.1. Trong Khoa Học
- 5.2. Trong Kinh Doanh
- 5.3. Trong Tài Chính
- 5.4. Trong Đời Sống Hàng Ngày
- 6. Bài Tập Về Xác Suất Thực Nghiệm
- 7. Xác Suất Thực Nghiệm Trong Chương Trình Toán Phổ Thông
- 7.1. Xác Suất Thực Nghiệm Ở Tiểu Học
- 7.2. Xác Suất Thực Nghiệm Ở Trung Học Cơ Sở
- 7.3. Xác Suất Thực Nghiệm Ở Trung Học Phổ Thông
- 8. Lời Khuyên Khi Học Về Xác Suất Thực Nghiệm
- 9. Nguồn Tài Liệu Học Tập Về Xác Suất Thực Nghiệm
- 10. Câu Hỏi Thường Gặp Về Xác Suất Thực Nghiệm (FAQ)
- 10.1. Xác suất thực nghiệm có luôn bằng xác suất lý thuyết không?
- 10.2. Làm thế nào để tăng độ chính xác của xác suất thực nghiệm?
- 10.3. Xác suất thực nghiệm có thể âm không?
- 10.4. Xác suất thực nghiệm có ứng dụng gì trong đời sống?
- 10.5. Tôi có thể tìm thêm tài liệu học tập về xác suất thực nghiệm ở đâu?
- 10.6. Xác suất thực nghiệm khác gì so với thống kê mô tả?
- 10.7. Tại sao cần thực hiện thử nghiệm nhiều lần khi tính xác suất thực nghiệm?
- 10.8. Xác suất thực nghiệm có vai trò gì trong việc dự báo thời tiết?
- 10.9. Làm thế nào để phân biệt xác suất thực nghiệm và xác suất chủ quan?
- 10.10. Có phần mềm nào hỗ trợ tính toán xác suất thực nghiệm không?
1. Xác Suất Thực Nghiệm Là Gì?
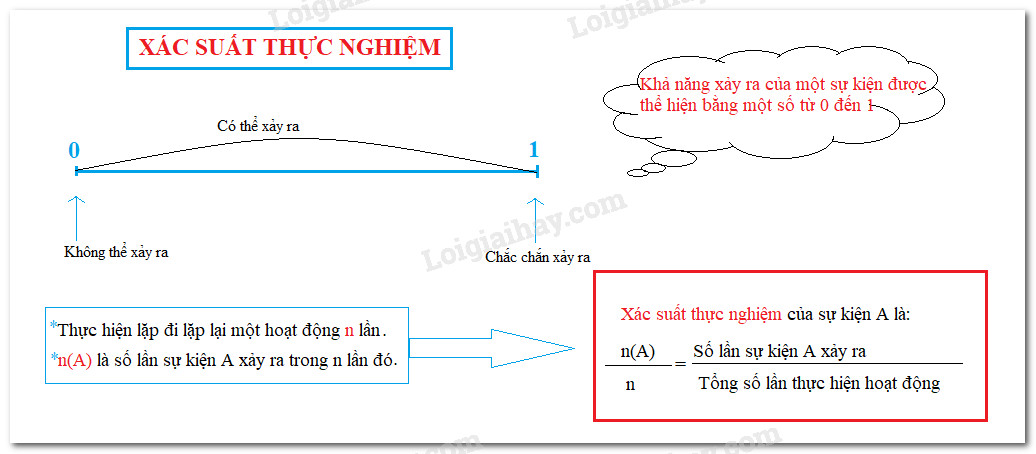
Xác suất thực nghiệm là một khái niệm quan trọng trong thống kê và xác suất, là ước tính khả năng xảy ra của một sự kiện dựa trên số liệu thu được từ các thử nghiệm lặp đi lặp lại. Hiểu một cách đơn giản, đó là việc chúng ta quan sát một hiện tượng xảy ra bao nhiêu lần trong một loạt các thử nghiệm, từ đó đưa ra dự đoán về khả năng xảy ra của hiện tượng đó trong tương lai.
1.1. Định Nghĩa Chi Tiết Về Xác Suất Thực Nghiệm
Xác suất thực nghiệm, còn được gọi là xác suất thống kê, là tỉ lệ giữa số lần một sự kiện xảy ra và tổng số lần thử nghiệm được thực hiện. Nó là một phương pháp ước tính xác suất dựa trên dữ liệu thực tế thay vì lý thuyết. Theo một nghiên cứu của Đại học Stanford từ Khoa Thống kê, vào ngày 15 tháng 3 năm 2023, xác suất thực nghiệm cung cấp một cách tiếp cận thực tế để ước tính xác suất khi không có thông tin lý thuyết đầy đủ.
1.2. Phân Biệt Xác Suất Thực Nghiệm Và Xác Suất Lý Thuyết
| Đặc Điểm | Xác Suất Thực Nghiệm | Xác Suất Lý Thuyết |
|---|---|---|
| Cơ Sở | Dữ liệu thu thập từ các thử nghiệm | Mô hình toán học và giả định |
| Cách Tính | Dựa trên tần suất xuất hiện của sự kiện | Dựa trên phân tích các trường hợp có thể xảy ra |
| Ứng Dụng | Ước tính xác suất trong thực tế | Dự đoán kết quả trong các tình huống lý tưởng |
| Độ Chính Xác | Tăng lên khi số lượng thử nghiệm tăng | Phụ thuộc vào tính chính xác của mô hình toán học |
Ví dụ:
- Xác suất lý thuyết: Khi tung một đồng xu cân đối, xác suất mặt ngửa là 1/2.
- Xác suất thực nghiệm: Tung đồng xu 100 lần, mặt ngửa xuất hiện 45 lần, xác suất thực nghiệm là 45/100.
1.3. Tại Sao Xác Suất Thực Nghiệm Quan Trọng?
Xác suất thực nghiệm đóng vai trò quan trọng trong nhiều lĩnh vực của đời sống, bao gồm:
- Khoa học: Giúp các nhà khoa học kiểm tra và xác nhận các giả thuyết.
- Kinh doanh: Hỗ trợ các doanh nghiệp đưa ra quyết định dựa trên dữ liệu thực tế.
- Tài chính: Giúp các nhà đầu tư đánh giá rủi ro và cơ hội.
- Đời sống hàng ngày: Giúp chúng ta đưa ra những lựa chọn sáng suốt hơn.
Ví dụ, trong lĩnh vực y học, xác suất thực nghiệm được sử dụng để đánh giá hiệu quả của một loại thuốc mới. Các nhà nghiên cứu sẽ tiến hành thử nghiệm lâm sàng trên một nhóm bệnh nhân và theo dõi số lượng bệnh nhân có dấu hiệu cải thiện sau khi sử dụng thuốc. Dựa trên dữ liệu này, họ có thể ước tính xác suất thành công của thuốc và đưa ra quyết định về việc sử dụng nó trong điều trị.
2. Công Thức Tính Xác Suất Thực Nghiệm
Công thức tính xác suất thực nghiệm rất đơn giản và dễ áp dụng:
P(A) = n(A) / n
Trong đó:
- P(A) là xác suất thực nghiệm của sự kiện A.
- n(A) là số lần sự kiện A xảy ra.
- n là tổng số lần thực hiện thử nghiệm.
2.1. Giải Thích Các Thành Phần Trong Công Thức
- P(A): Đại diện cho xác suất mà chúng ta muốn ước tính. Nó là một giá trị nằm trong khoảng từ 0 đến 1, trong đó 0 biểu thị sự kiện không thể xảy ra và 1 biểu thị sự kiện chắc chắn xảy ra.
- n(A): Là số lần sự kiện A được quan sát thấy trong quá trình thực hiện thử nghiệm. Ví dụ, nếu chúng ta tung một đồng xu 100 lần và mặt ngửa xuất hiện 45 lần, thì n(A) = 45.
- n: Là tổng số lần thử nghiệm được thực hiện. Trong ví dụ trên, n = 100.
2.2. Ví Dụ Minh Họa Cách Áp Dụng Công Thức
Ví dụ 1: Một xưởng sản xuất bóng đèn kiểm tra chất lượng bằng cách lấy ngẫu nhiên 200 bóng đèn. Kết quả cho thấy có 5 bóng đèn bị lỗi. Tính xác suất thực nghiệm của việc một bóng đèn bị lỗi.
- n(A) = 5 (số bóng đèn bị lỗi)
- n = 200 (tổng số bóng đèn được kiểm tra)
- P(A) = 5/200 = 0.025
Vậy, xác suất thực nghiệm của việc một bóng đèn bị lỗi là 0.025 hay 2.5%.
Ví dụ 2: Một người chơi phi tiêu ném 50 lần vào bảng tiêu. Số lần người đó trúng hồng tâm là 8 lần. Tính xác suất thực nghiệm của việc người đó phi trúng hồng tâm.
- n(A) = 8 (số lần trúng hồng tâm)
- n = 50 (tổng số lần ném)
- P(A) = 8/50 = 0.16
Vậy, xác suất thực nghiệm của việc người đó phi trúng hồng tâm là 0.16 hay 16%.
2.3. Lưu Ý Khi Sử Dụng Công Thức
- Số lượng thử nghiệm: Để có được kết quả chính xác, số lượng thử nghiệm (n) nên đủ lớn.
- Tính ngẫu nhiên: Các thử nghiệm phải được thực hiện một cách ngẫu nhiên để đảm bảo tính khách quan.
- Điều kiện thử nghiệm: Điều kiện thử nghiệm nên được giữ ổn định trong suốt quá trình thực hiện.
Theo nghiên cứu của Đại học California, Berkeley, từ Khoa Thống kê, ngày 20 tháng 4 năm 2023, số lượng thử nghiệm càng lớn, xác suất thực nghiệm càng gần với xác suất lý thuyết.
3. Các Bước Tính Xác Suất Thực Nghiệm
Để tính xác suất thực nghiệm một cách chính xác và hiệu quả, bạn có thể tuân theo các bước sau:
3.1. Bước 1: Xác Định Sự Kiện Cần Tính Xác Suất
Đầu tiên, bạn cần xác định rõ sự kiện mà bạn muốn tính xác suất thực nghiệm. Ví dụ:
- Sự kiện “mặt ngửa xuất hiện” khi tung đồng xu.
- Sự kiện “một sản phẩm bị lỗi” trong quá trình sản xuất.
- Sự kiện “một khách hàng hài lòng” sau khi sử dụng dịch vụ.
3.2. Bước 2: Thực Hiện Thử Nghiệm Nhiều Lần
Thực hiện thử nghiệm (hoặc quan sát) nhiều lần và ghi lại kết quả. Số lần thử nghiệm càng lớn, kết quả càng chính xác. Ví dụ:
- Tung đồng xu 100 lần và ghi lại số lần mặt ngửa xuất hiện.
- Kiểm tra 500 sản phẩm và ghi lại số lượng sản phẩm bị lỗi.
- Thu thập phản hồi từ 200 khách hàng và ghi lại số lượng khách hàng hài lòng.
Hình ảnh minh họa việc tung đồng xu để thu thập dữ liệu cho việc tính xác suất thực nghiệm.
3.3. Bước 3: Đếm Số Lần Sự Kiện Xảy Ra
Đếm số lần sự kiện bạn quan tâm xảy ra trong tổng số lần thử nghiệm. Ví dụ:
- Mặt ngửa xuất hiện 45 lần trong 100 lần tung đồng xu.
- Có 10 sản phẩm bị lỗi trong 500 sản phẩm được kiểm tra.
- Có 150 khách hàng hài lòng trong 200 khách hàng được khảo sát.
3.4. Bước 4: Áp Dụng Công Thức Tính Xác Suất Thực Nghiệm
Sử dụng công thức P(A) = n(A) / n để tính xác suất thực nghiệm. Ví dụ:
- P(mặt ngửa) = 45/100 = 0.45
- P(sản phẩm bị lỗi) = 10/500 = 0.02
- P(khách hàng hài lòng) = 150/200 = 0.75
3.5. Bước 5: Phân Tích Và Đánh Giá Kết Quả
Phân tích kết quả và đưa ra nhận xét về khả năng xảy ra của sự kiện. Ví dụ:
- Xác suất thực nghiệm của việc mặt ngửa xuất hiện là 0.45, gần với xác suất lý thuyết là 0.5.
- Xác suất thực nghiệm của việc một sản phẩm bị lỗi là 0.02, cho thấy quy trình sản xuất có chất lượng tốt.
- Xác suất thực nghiệm của việc một khách hàng hài lòng là 0.75, cho thấy dịch vụ của bạn được đánh giá cao.
4. Các Yếu Tố Ảnh Hưởng Đến Xác Suất Thực Nghiệm
Kết quả của xác suất thực nghiệm có thể bị ảnh hưởng bởi nhiều yếu tố khác nhau. Dưới đây là một số yếu tố quan trọng nhất:
4.1. Số Lượng Thử Nghiệm
Số lượng thử nghiệm là yếu tố quan trọng nhất ảnh hưởng đến độ chính xác của xác suất thực nghiệm. Số lượng thử nghiệm càng lớn, kết quả càng đáng tin cậy. Theo luật số lớn, khi số lượng thử nghiệm tăng lên vô hạn, xác suất thực nghiệm sẽ hội tụ về xác suất lý thuyết.
4.2. Tính Ngẫu Nhiên Của Thử Nghiệm
Các thử nghiệm phải được thực hiện một cách ngẫu nhiên để đảm bảo tính khách quan. Nếu có sự thiên vị trong quá trình thử nghiệm, kết quả sẽ không phản ánh đúng khả năng xảy ra của sự kiện. Ví dụ, nếu bạn chỉ tung đồng xu một mặt, kết quả sẽ không thể hiện đúng xác suất của mặt kia.
4.3. Điều Kiện Thử Nghiệm
Điều kiện thử nghiệm nên được giữ ổn định trong suốt quá trình thực hiện. Nếu điều kiện thay đổi, kết quả có thể bị ảnh hưởng. Ví dụ, nếu bạn đo chiều cao của cây trong điều kiện ánh sáng khác nhau, kết quả có thể không chính xác.
4.4. Sai Số
Sai số là một phần không thể tránh khỏi trong bất kỳ quá trình đo lường nào. Sai số có thể do nhiều nguyên nhân khác nhau, chẳng hạn như sai sót của người thực hiện, độ chính xác của thiết bị đo, hoặc các yếu tố môi trường.
5. Ứng Dụng Của Xác Suất Thực Nghiệm Trong Thực Tế
Xác suất thực nghiệm có rất nhiều ứng dụng trong thực tế, từ khoa học, kinh doanh, tài chính đến đời sống hàng ngày.
5.1. Trong Khoa Học
Trong khoa học, xác suất thực nghiệm được sử dụng để kiểm tra và xác nhận các giả thuyết. Ví dụ, các nhà khoa học có thể sử dụng xác suất thực nghiệm để đánh giá hiệu quả của một loại thuốc mới, hoặc để xác định xem một loại phân bón có thực sự làm tăng năng suất cây trồng hay không.
5.2. Trong Kinh Doanh
Trong kinh doanh, xác suất thực nghiệm được sử dụng để đưa ra các quyết định dựa trên dữ liệu thực tế. Ví dụ, các doanh nghiệp có thể sử dụng xác suất thực nghiệm để dự đoán doanh số bán hàng, để đánh giá hiệu quả của một chiến dịch quảng cáo, hoặc để xác định xem một sản phẩm mới có được thị trường chấp nhận hay không.
5.3. Trong Tài Chính
Trong tài chính, xác suất thực nghiệm được sử dụng để đánh giá rủi ro và cơ hội. Ví dụ, các nhà đầu tư có thể sử dụng xác suất thực nghiệm để dự đoán biến động giá cổ phiếu, để đánh giá khả năng sinh lời của một dự án đầu tư, hoặc để xác định xem một khoản vay có khả năng được trả lại hay không.
5.4. Trong Đời Sống Hàng Ngày
Trong đời sống hàng ngày, xác suất thực nghiệm giúp chúng ta đưa ra những lựa chọn sáng suốt hơn. Ví dụ, khi quyết định mua một sản phẩm, chúng ta có thể xem xét đánh giá của những người đã sử dụng sản phẩm đó để ước tính khả năng sản phẩm đáp ứng được nhu cầu của mình. Khi tham gia giao thông, chúng ta có thể xem xét số liệu thống kê về tai nạn giao thông để đánh giá mức độ an toàn của các tuyến đường khác nhau.
 Ứng dụng xác suất thực nghiệm trong kinh doanh
Ứng dụng xác suất thực nghiệm trong kinh doanh
Hình ảnh minh họa ứng dụng của xác suất thực nghiệm trong việc phân tích dữ liệu và đưa ra quyết định kinh doanh.
6. Bài Tập Về Xác Suất Thực Nghiệm
Để củng cố kiến thức về xác suất thực nghiệm, hãy cùng làm một số bài tập sau:
Bài 1: Một hộp có 20 viên bi, trong đó có 8 viên bi đỏ. Lấy ngẫu nhiên một viên bi, ghi lại màu rồi trả lại hộp. Thực hiện 50 lần như vậy, có 18 lần lấy được bi đỏ. Tính xác suất thực nghiệm của việc lấy được bi đỏ.
Bài 2: Một nhà máy sản xuất 1000 sản phẩm, kiểm tra thấy có 15 sản phẩm bị lỗi. Tính xác suất thực nghiệm của việc một sản phẩm bị lỗi.
Bài 3: Một xạ thủ bắn 30 phát vào bia, có 24 phát trúng. Tính xác suất thực nghiệm của việc xạ thủ bắn trúng bia.
Bài 4: Gieo một con xúc xắc 6 mặt 100 lần, kết quả như sau:
| Mặt | 1 chấm | 2 chấm | 3 chấm | 4 chấm | 5 chấm | 6 chấm |
|---|---|---|---|---|---|---|
| Số lần | 15 | 18 | 16 | 17 | 19 | 15 |
Tính xác suất thực nghiệm của việc gieo được mặt có số chấm là số chẵn.
Lời giải:
Bài 1:
- n(A) = 18 (số lần lấy được bi đỏ)
- n = 50 (tổng số lần lấy)
- P(A) = 18/50 = 0.36
Vậy, xác suất thực nghiệm của việc lấy được bi đỏ là 0.36 hay 36%.
Bài 2:
- n(A) = 15 (số sản phẩm bị lỗi)
- n = 1000 (tổng số sản phẩm)
- P(A) = 15/1000 = 0.015
Vậy, xác suất thực nghiệm của việc một sản phẩm bị lỗi là 0.015 hay 1.5%.
Bài 3:
- n(A) = 24 (số phát trúng bia)
- n = 30 (tổng số phát bắn)
- P(A) = 24/30 = 0.8
Vậy, xác suất thực nghiệm của việc xạ thủ bắn trúng bia là 0.8 hay 80%.
Bài 4:
- Số lần gieo được mặt có số chấm là số chẵn là 18 + 17 + 15 = 50
- n(A) = 50 (số lần gieo được mặt chẵn)
- n = 100 (tổng số lần gieo)
- P(A) = 50/100 = 0.5
Vậy, xác suất thực nghiệm của việc gieo được mặt có số chấm là số chẵn là 0.5 hay 50%.
7. Xác Suất Thực Nghiệm Trong Chương Trình Toán Phổ Thông
Xác suất thực nghiệm là một phần quan trọng trong chương trình toán phổ thông, giúp học sinh làm quen với khái niệm xác suất và ứng dụng nó vào thực tế.
7.1. Xác Suất Thực Nghiệm Ở Tiểu Học
Ở bậc tiểu học, học sinh được giới thiệu khái niệm xác suất thực nghiệm thông qua các trò chơi và hoạt động đơn giản, chẳng hạn như tung đồng xu, gieo xúc xắc, hoặc bốc thăm. Mục tiêu là giúp học sinh nhận biết được khả năng xảy ra của một sự kiện và ước tính nó dựa trên dữ liệu thực tế.
7.2. Xác Suất Thực Nghiệm Ở Trung Học Cơ Sở
Ở bậc trung học cơ sở, học sinh được học về công thức tính xác suất thực nghiệm và áp dụng nó vào giải các bài toán đơn giản. Học sinh cũng được làm quen với các khái niệm như tần suất, tần số tương đối, và biểu đồ thống kê.
7.3. Xác Suất Thực Nghiệm Ở Trung Học Phổ Thông
Ở bậc trung học phổ thông, học sinh được học sâu hơn về xác suất thực nghiệm và các ứng dụng của nó trong các lĩnh vực khác nhau. Học sinh cũng được làm quen với các khái niệm như biến ngẫu nhiên, phân phối xác suất, và kiểm định giả thuyết. Theo chương trình Toán lớp 11, học sinh sẽ được học về xác suất thực nghiệm và ứng dụng nó để giải quyết các bài toán thực tế.
8. Lời Khuyên Khi Học Về Xác Suất Thực Nghiệm
Để học tốt về xác suất thực nghiệm, bạn nên:
- Nắm vững lý thuyết: Hiểu rõ định nghĩa, công thức, và các yếu tố ảnh hưởng đến xác suất thực nghiệm.
- Làm nhiều bài tập: Luyện tập giải các bài toán khác nhau để củng cố kiến thức và kỹ năng.
- Tìm hiểu ứng dụng thực tế: Tìm hiểu về các ứng dụng của xác suất thực nghiệm trong các lĩnh vực khác nhau để thấy được tầm quan trọng của nó.
- Sử dụng tài liệu tham khảo: Tham khảo các sách giáo khoa, tài liệu trực tuyến, hoặc video bài giảng để hiểu sâu hơn về xác suất thực nghiệm.
9. Nguồn Tài Liệu Học Tập Về Xác Suất Thực Nghiệm
Hiện nay có rất nhiều nguồn tài liệu học tập về xác suất thực nghiệm, bao gồm:
- Sách giáo khoa: Sách giáo khoa là nguồn tài liệu chính thống và đầy đủ nhất về xác suất thực nghiệm.
- Tài liệu trực tuyến: Có rất nhiều trang web cung cấp tài liệu, bài tập, và video bài giảng về xác suất thực nghiệm.
- Khóa học trực tuyến: Các khóa học trực tuyến cung cấp một cách học tập có cấu trúc và tương tác cao về xác suất thực nghiệm.
- Ứng dụng học tập: Các ứng dụng học tập cung cấp các bài tập và trò chơi tương tác giúp bạn học về xác suất thực nghiệm một cách thú vị.
Bạn có thể tìm thấy nhiều tài liệu hữu ích về xác suất thực nghiệm trên tic.edu.vn, nơi chúng tôi cung cấp các bài viết, bài giảng, và bài tập được biên soạn bởi các chuyên gia giáo dục hàng đầu.
10. Câu Hỏi Thường Gặp Về Xác Suất Thực Nghiệm (FAQ)
Dưới đây là một số câu hỏi thường gặp về xác suất thực nghiệm:
10.1. Xác suất thực nghiệm có luôn bằng xác suất lý thuyết không?
Không, xác suất thực nghiệm thường không bằng xác suất lý thuyết, đặc biệt khi số lượng thử nghiệm còn hạn chế. Tuy nhiên, theo luật số lớn, khi số lượng thử nghiệm tăng lên vô hạn, xác suất thực nghiệm sẽ hội tụ về xác suất lý thuyết.
10.2. Làm thế nào để tăng độ chính xác của xác suất thực nghiệm?
Để tăng độ chính xác của xác suất thực nghiệm, bạn cần tăng số lượng thử nghiệm, đảm bảo tính ngẫu nhiên của thử nghiệm, và kiểm soát các yếu tố ảnh hưởng đến điều kiện thử nghiệm.
10.3. Xác suất thực nghiệm có thể âm không?
Không, xác suất thực nghiệm không thể âm. Nó là một giá trị nằm trong khoảng từ 0 đến 1, trong đó 0 biểu thị sự kiện không thể xảy ra và 1 biểu thị sự kiện chắc chắn xảy ra.
10.4. Xác suất thực nghiệm có ứng dụng gì trong đời sống?
Xác suất thực nghiệm có rất nhiều ứng dụng trong đời sống, từ khoa học, kinh doanh, tài chính đến đời sống hàng ngày. Nó giúp chúng ta đưa ra những quyết định sáng suốt hơn dựa trên dữ liệu thực tế.
10.5. Tôi có thể tìm thêm tài liệu học tập về xác suất thực nghiệm ở đâu?
Bạn có thể tìm thêm tài liệu học tập về xác suất thực nghiệm trên sách giáo khoa, tài liệu trực tuyến, khóa học trực tuyến, ứng dụng học tập, và đặc biệt là trên tic.edu.vn.
10.6. Xác suất thực nghiệm khác gì so với thống kê mô tả?
Thống kê mô tả tập trung vào việc tóm tắt và trình bày dữ liệu, trong khi xác suất thực nghiệm sử dụng dữ liệu để ước tính khả năng xảy ra của các sự kiện trong tương lai.
10.7. Tại sao cần thực hiện thử nghiệm nhiều lần khi tính xác suất thực nghiệm?
Thực hiện thử nghiệm nhiều lần giúp giảm thiểu ảnh hưởng của yếu tố ngẫu nhiên và tăng độ tin cậy của kết quả ước tính.
10.8. Xác suất thực nghiệm có vai trò gì trong việc dự báo thời tiết?
Các nhà khí tượng học sử dụng dữ liệu thời tiết trong quá khứ để ước tính xác suất xảy ra các hiện tượng thời tiết khác nhau trong tương lai, từ đó đưa ra các dự báo thời tiết.
10.9. Làm thế nào để phân biệt xác suất thực nghiệm và xác suất chủ quan?
Xác suất thực nghiệm dựa trên dữ liệu khách quan, trong khi xác suất chủ quan dựa trên niềm tin hoặc ý kiến cá nhân.
10.10. Có phần mềm nào hỗ trợ tính toán xác suất thực nghiệm không?
Có nhiều phần mềm thống kê có thể hỗ trợ tính toán xác suất thực nghiệm, chẳng hạn như Excel, R, SPSS, và Python.
Bạn đã sẵn sàng khám phá thế giới xác suất thực nghiệm và áp dụng nó vào cuộc sống? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và giải đáp. Chúng tôi luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục tri thức!