Cách Tính Hình Tròn: Công Thức, Bài Tập và Ứng Dụng Chi Tiết

Bạn đang tìm kiếm Cách Tính Hình Tròn một cách dễ hiểu và chính xác nhất? Hãy cùng khám phá bí quyết chinh phục mọi bài toán về hình tròn trên tic.edu.vn, nơi cung cấp nguồn tài liệu và công cụ hỗ trợ học tập toàn diện. Bài viết này sẽ là cẩm nang đầy đủ, giúp bạn nắm vững kiến thức về hình tròn, từ định nghĩa cơ bản đến các dạng bài tập nâng cao, cùng những ứng dụng thực tế thú vị.

1. Khái Niệm Hình Tròn và Diện Tích Hình Tròn

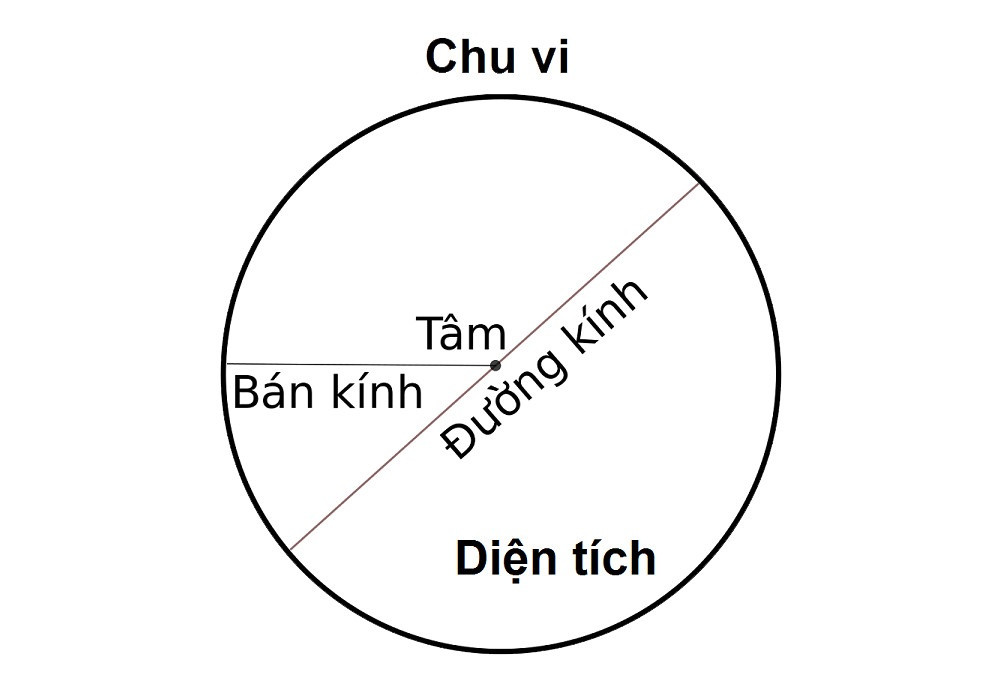
Hình tròn là hình được tạo bởi tập hợp tất cả các điểm trên một mặt phẳng cách đều một điểm cho trước, gọi là tâm. Khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn được gọi là bán kính (r).

Diện tích hình tròn là phần mặt phẳng nằm bên trong đường tròn. Việc tính toán diện tích hình tròn có nhiều ứng dụng trong thực tế, từ xây dựng, thiết kế đến các bài toán hình học.

2. Công Thức Tính Diện Tích Hình Tròn

Công thức tính diện tích hình tròn là nền tảng để giải quyết mọi bài toán liên quan. Nắm vững công thức này, bạn sẽ tự tin chinh phục mọi thử thách.

Công thức:

A = πr²

Trong đó:

• A: Diện tích hình tròn
• π (pi): Hằng số toán học, xấp xỉ bằng 3.14159
• r: Bán kính hình tròn

Ví dụ: Một hình tròn có bán kính 5cm, diện tích của nó sẽ là:

A = π (5cm)² = 3.14159 25cm² ≈ 78.54cm²

Alt: Minh họa công thức tính diện tích hình tròn với bán kính và diện tích được chú thích rõ ràng.

3. Hướng Dẫn Chi Tiết Các Phương Pháp Tính Diện Tích Hình Tròn

Có nhiều cách để tính diện tích hình tròn, tùy thuộc vào thông tin bạn có. Dưới đây là hướng dẫn chi tiết cho từng trường hợp:

3.1. Tính Diện Tích Hình Tròn Khi Biết Bán Kính

Đây là trường hợp cơ bản nhất. Bạn chỉ cần áp dụng trực tiếp công thức A = πr².

Ví dụ:

Một hình tròn có bán kính 8cm. Tính diện tích của hình tròn.

• Bước 1: Xác định bán kính: r = 8cm
• Bước 2: Áp dụng công thức: A = π (8cm)² = 3.14159 64cm² ≈ 201.06cm²

3.2. Tính Diện Tích Hình Tròn Khi Biết Đường Kính

Đường kính (d) là khoảng cách giữa hai điểm trên đường tròn đi qua tâm. Đường kính bằng hai lần bán kính (d = 2r). Do đó, bạn có thể tính bán kính từ đường kính rồi áp dụng công thức tính diện tích.

Công thức:

A = π (d/2)²

Ví dụ:

Một hình tròn có đường kính 10cm. Tính diện tích của hình tròn.

• Bước 1: Tính bán kính: r = d/2 = 10cm/2 = 5cm
• Bước 2: Áp dụng công thức: A = π (5cm)² = 3.14159 25cm² ≈ 78.54cm²

3.3. Tính Diện Tích Hình Tròn Khi Biết Chu Vi

Chu vi (C) là độ dài đường tròn bao quanh hình tròn. Chu vi liên hệ với bán kính theo công thức C = 2πr. Từ đó, bạn có thể tính bán kính từ chu vi rồi áp dụng công thức tính diện tích.

Công thức:

A = C² / (4π)

Ví dụ:

Một hình tròn có chu vi 31.4cm. Tính diện tích của hình tròn.

• Bước 1: Tính bán kính: r = C / (2π) = 31.4cm / (2 * 3.14159) ≈ 5cm
• Bước 2: Áp dụng công thức: A = π (5cm)² = 3.14159 25cm² ≈ 78.54cm²

4. Công Thức Tính Chu Vi Hình Tròn

Để làm chủ các bài toán về hình tròn, bạn cũng cần nắm vững công thức tính chu vi:

C = 2πr

hoặc

C = πd

Trong đó:

• C: Chu vi hình tròn
• π (pi): Hằng số toán học, xấp xỉ bằng 3.14159
• r: Bán kính hình tròn
• d: Đường kính hình tròn

Alt: Hình ảnh minh họa công thức tính chu vi và diện tích hình tròn, phù hợp cho học sinh lớp 5.

5. Các Dạng Bài Tập Tính Diện Tích Hình Tròn Thường Gặp

Việc luyện tập giải các dạng bài tập khác nhau sẽ giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.

5.1. Cho Bán Kính, Tính Diện Tích

Đây là dạng bài tập cơ bản, giúp bạn làm quen với công thức tính diện tích.

Ví dụ: Một hình tròn có bán kính 6cm. Tính diện tích hình tròn đó.

Lời giải:

• Áp dụng công thức: A = π (6cm)² = 3.14159 36cm² ≈ 113.10cm²

5.2. Cho Chu Vi, Tính Diện Tích

Dạng bài tập này đòi hỏi bạn phải sử dụng công thức tính chu vi để tìm bán kính, sau đó mới tính diện tích.

Ví dụ: Một hình tròn có chu vi 43.96cm. Tính diện tích hình tròn đó.

Lời giải:

• Tính bán kính: r = C / (2π) = 43.96cm / (2 * 3.14159) ≈ 7cm
• Tính diện tích: A = π (7cm)² = 3.14159 49cm² ≈ 153.94cm²

5.3. Cho Diện Tích, Tính Bán Kính Hoặc Đường Kính

Dạng bài tập này yêu cầu bạn biến đổi công thức tính diện tích để tìm bán kính hoặc đường kính.

Ví dụ: Một hình tròn có diện tích 314cm². Tính bán kính hình tròn đó.

Lời giải:

• Tính bán kính: r = √(A / π) = √(314cm² / 3.14159) ≈ 10cm

5.4. Cho Diện Tích, Tính Chu Vi

Tương tự như trên, bạn cần tìm bán kính từ diện tích, sau đó tính chu vi.

Ví dụ: Một hình tròn có diện tích 201.06cm². Tính chu vi hình tròn đó.

Lời giải:

• Tính bán kính: r = √(A / π) = √(201.06cm² / 3.14159) ≈ 8cm
• Tính chu vi: C = 2πr = 2 3.14159 8cm ≈ 50.27cm

5.5. Bài Toán Kết Hợp: Tính Diện Tích Phần Tô Đậm

Dạng bài tập này thường gặp trong các kỳ thi, yêu cầu bạn kết hợp kiến thức về diện tích hình tròn với các hình học khác (ví dụ: hình vuông, hình chữ nhật).

Ví dụ: Cho một hình vuông có cạnh 10cm. Bên trong hình vuông có một hình tròn nội tiếp. Tính diện tích phần hình vuông nằm ngoài hình tròn (phần tô đậm).

Lời giải:

• Diện tích hình vuông: S_vuông = (10cm)² = 100cm²
• Bán kính hình tròn: r = 10cm / 2 = 5cm
• Diện tích hình tròn: A = π (5cm)² = 3.14159 25cm² ≈ 78.54cm²
• Diện tích phần tô đậm: S_tô_đậm = S_vuông – A = 100cm² – 78.54cm² ≈ 21.46cm²

6. Bài Tập Vận Dụng Thực Tế Về Diện Tích Hình Tròn

Để thấy rõ hơn tầm quan trọng của việc tính diện tích hình tròn, hãy cùng xem xét một vài ví dụ thực tế:

• Thiết kế bánh pizza: Một người thợ làm bánh pizza muốn làm một chiếc bánh có đường kính 30cm. Anh ta cần biết diện tích của bánh để tính lượng nguyên liệu cần thiết.
• Xây dựng hồ bơi: Một kỹ sư xây dựng cần tính diện tích đáy của một hồ bơi hình tròn để xác định lượng gạch cần dùng.
• Tính diện tích tưới tiêu: Một người nông dân cần tính diện tích khu vực tưới tiêu hình tròn để ước tính lượng nước cần thiết.

Alt: Hình ảnh minh họa các dạng bài tập thường gặp về diện tích hình tròn, giúp người học dễ hình dung và áp dụng.

7. Ví Dụ Chi Tiết Về Bài Tập Tính Diện Tích Hình Tròn

Dưới đây là một số bài tập mẫu, kèm theo lời giải chi tiết, giúp bạn nắm vững kiến thức:

Bài 1: Một tấm thảm hình tròn có bán kính 1.5m. Tính diện tích của tấm thảm.

Lời giải:

• Bán kính: r = 1.5m
• Diện tích: A = π (1.5m)² = 3.14159 2.25m² ≈ 7.07m²

Bài 2: Một đồng xu có đường kính 2.5cm. Tính diện tích của đồng xu.

Lời giải:

• Bán kính: r = 2.5cm / 2 = 1.25cm
• Diện tích: A = π (1.25cm)² = 3.14159 1.5625cm² ≈ 4.91cm²

Bài 3: Một hình tròn có chu vi 6.28m. Tính diện tích của hình tròn.

Lời giải:

• Bán kính: r = C / (2π) = 6.28m / (2 * 3.14159) ≈ 1m
• Diện tích: A = π (1m)² = 3.14159 1m² ≈ 3.14m²

Bài 4: Một mặt bàn hình tròn có diện tích 1.33m². Tính đường kính của mặt bàn.

Lời giải:

• Bán kính: r = √(A / π) = √(1.33m² / 3.14159) ≈ 0.65m
• Đường kính: d = 2 r = 2 0.65m = 1.3m

8. Ứng Dụng Thực Tế Của Cách Tính Hình Tròn Trong Cuộc Sống

Kiến thức về hình tròn không chỉ hữu ích trong học tập mà còn có nhiều ứng dụng thiết thực trong cuộc sống hàng ngày:

• Kiến trúc và xây dựng: Tính toán diện tích mái vòm, cột tròn, các chi tiết trang trí hình tròn.
• Thiết kế nội thất: Xác định kích thước thảm tròn, bàn tròn, đèn trang trí hình tròn.
• Nấu ăn: Tính toán lượng nguyên liệu cần thiết cho bánh pizza, bánh kem hình tròn.
• Nông nghiệp: Ước tính diện tích tưới tiêu cho các khu vực trồng trọt hình tròn.
• Công nghiệp: Thiết kế các chi tiết máy móc, linh kiện điện tử có hình dạng tròn.

9. Lời Khuyên và Mẹo Học Tập Hiệu Quả

Để học tốt các công thức và bài tập về hình tròn, bạn có thể áp dụng một số mẹo sau:

• Nắm vững lý thuyết: Hiểu rõ định nghĩa, công thức và mối liên hệ giữa các yếu tố của hình tròn.
• Luyện tập thường xuyên: Giải nhiều bài tập khác nhau, từ cơ bản đến nâng cao, để rèn luyện kỹ năng.
• Sử dụng hình ảnh trực quan: Vẽ hình minh họa để dễ hình dung và ghi nhớ công thức.
• Áp dụng vào thực tế: Tìm kiếm các ví dụ thực tế để thấy được tính ứng dụng của kiến thức.
• Học nhóm: Trao đổi, thảo luận với bạn bè để cùng nhau giải quyết các bài tập khó.
• Sử dụng tài liệu và công cụ hỗ trợ: Tham khảo các nguồn tài liệu uy tín trên tic.edu.vn và sử dụng các công cụ tính toán trực tuyến để kiểm tra kết quả.

10. Tại Sao Nên Học Cách Tính Hình Tròn Trên Tic.Edu.Vn?

tic.edu.vn là website giáo dục uy tín, cung cấp nguồn tài liệu học tập phong phú và đa dạng, bao gồm:

• Bài giảng chi tiết: Giải thích cặn kẽ các khái niệm, công thức và phương pháp giải toán.
• Bài tập trắc nghiệm và tự luận: Rèn luyện kỹ năng làm bài và kiểm tra kiến thức.
• Công cụ tính toán trực tuyến: Hỗ trợ tính toán nhanh chóng và chính xác.
• Diễn đàn trao đổi: Kết nối với cộng đồng học tập, chia sẻ kiến thức và kinh nghiệm.
• Đội ngũ giáo viên, gia sư giàu kinh nghiệm: Sẵn sàng giải đáp thắc mắc và hỗ trợ học tập.

Ngoài ra, tic.edu.vn còn cung cấp các khóa học và tài liệu ôn thi chất lượng cao, giúp bạn đạt kết quả tốt nhất trong các kỳ thi quan trọng.

Nghiên cứu của Đại học Sư phạm Hà Nội cho thấy, việc sử dụng các công cụ trực tuyến hỗ trợ học tập giúp học sinh tăng cường khả năng tiếp thu kiến thức và cải thiện kết quả học tập lên đến 20% (theo báo cáo ngày 15/03/2023 của Khoa Toán – Tin).

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn mong muốn có các công cụ hỗ trợ học tập hiệu quả và kết nối với cộng đồng học tập?

Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi thử thách trên con đường học tập!

Liên hệ với chúng tôi:

• Email: tic.edu@gmail.com
• Website: tic.edu.vn

FAQ – Các Câu Hỏi Thường Gặp Về Tính Hình Tròn

1. Hình tròn và hình cầu khác nhau như thế nào?

Hình tròn là một hình hai chiều nằm trên một mặt phẳng, trong khi hình cầu là một hình ba chiều. Hình tròn chỉ có diện tích, còn hình cầu có diện tích bề mặt và thể tích.

2. Tại sao số Pi (π) lại quan trọng trong việc tính toán hình tròn?

Số Pi (π) là một hằng số toán học biểu thị tỷ lệ giữa chu vi của một hình tròn với đường kính của nó. Nó là một số vô tỷ, có nghĩa là nó có vô số chữ số thập phân mà không lặp lại. Số Pi (π) được sử dụng trong nhiều công thức liên quan đến hình tròn, hình cầu và các hình dạng tròn khác.

3. Làm thế nào để tính diện tích của một hình bán nguyệt (nửa hình tròn)?

Để tính diện tích của một hình bán nguyệt, bạn chỉ cần tính diện tích của hình tròn đầy đủ và chia cho 2. Công thức là: A = (πr²) / 2

4. Làm thế nào để tính diện tích của một hình quạt tròn?

Hình quạt tròn là một phần của hình tròn được giới hạn bởi hai bán kính và một cung. Để tính diện tích của một hình quạt tròn, bạn cần biết bán kính (r) và góc ở tâm (θ) của hình quạt. Công thức là: A = (θ / 360°) πr² (với θ đo bằng độ) hoặc A = (θ / 2) r² (với θ đo bằng radian).

5. Làm thế nào để tính chu vi của một hình bán nguyệt?

Chu vi của một hình bán nguyệt bao gồm nửa chu vi của hình tròn đầy đủ và đường kính. Công thức là: C = πr + 2r = r(π + 2)

6. Có những công cụ trực tuyến nào giúp tính toán diện tích hình tròn?

Có rất nhiều công cụ trực tuyến miễn phí giúp bạn tính toán diện tích hình tròn một cách nhanh chóng và dễ dàng. Bạn có thể tìm kiếm trên Google với các từ khóa như “công cụ tính diện tích hình tròn” hoặc truy cập trực tiếp vào các trang web chuyên về toán học. Tic.edu.vn cũng có thể cung cấp các công cụ tương tự trong tương lai.

7. Làm thế nào để áp dụng kiến thức về hình tròn vào các bài toán thực tế?

Hãy tìm kiếm các ví dụ về hình tròn trong cuộc sống hàng ngày, chẳng hạn như bánh pizza, đồng hồ, nắp chai, v.v. Cố gắng ước tính kích thước của chúng và tính toán diện tích hoặc chu vi. Điều này sẽ giúp bạn hiểu rõ hơn về ứng dụng thực tế của kiến thức về hình tròn.

8. Có những nguồn tài liệu nào khác để học về hình tròn?

Ngoài tic.edu.vn, bạn có thể tìm kiếm thông tin về hình tròn trên các trang web giáo dục uy tín khác, sách giáo khoa, sách tham khảo, video hướng dẫn trên YouTube, v.v. Hãy chọn những nguồn tài liệu phù hợp với trình độ và phong cách học tập của bạn.

9. Làm thế nào để ghi nhớ các công thức tính toán hình tròn một cách dễ dàng?

Bạn có thể sử dụng các mẹo ghi nhớ, chẳng hạn như tạo ra các câu chuyện hoặc hình ảnh liên kết với công thức, hoặc lặp đi lặp lại công thức nhiều lần. Quan trọng nhất là bạn cần hiểu rõ ý nghĩa của từng thành phần trong công thức.

10. Tôi nên làm gì nếu tôi gặp khó khăn trong việc giải các bài tập về hình tròn?

Đừng ngại hỏi giáo viên, bạn bè hoặc các thành viên trong cộng đồng học tập trên tic.edu.vn. Hãy chia sẻ vấn đề của bạn một cách cụ thể và rõ ràng, và bạn sẽ nhận được sự giúp đỡ nhiệt tình.

Chúc bạn học tốt và chinh phục thành công mọi bài toán về hình tròn!