Cách Tính Hình Thang Cân Chi Tiết Nhất: Công Thức, Bài Tập

Cách Tính Hình Thang Cân không còn là nỗi lo với bài viết này từ tic.edu.vn. Chúng tôi sẽ cung cấp công thức, bài tập và ứng dụng thực tế, giúp bạn nắm vững kiến thức về hình thang cân một cách dễ dàng, hiệu quả.

1. Tổng Quan Lý Thuyết Về Hình Thang Cân

Trước khi khám phá các công thức tính toán, hãy cùng tic.edu.vn ôn lại những kiến thức cơ bản nhất về hình thang cân để đảm bảo bạn có nền tảng vững chắc nhé.

1.1. Định Nghĩa Hình Thang và Hình Thang Cân

Hình thang là một tứ giác lồi đặc biệt, nổi bật với một cặp cạnh đối diện song song, được gọi là cạnh đáy. Hai cạnh còn lại, không song song, được gọi là cạnh bên. Theo “Hình học 10 nâng cao” của nhà xuất bản Giáo dục Việt Nam, hình thang là một phần quan trọng của chương trình học.

Hình thang cân là một trường hợp đặc biệt của hình thang, với hai cạnh bên có độ dài bằng nhau. Điều này dẫn đến hai góc kề một đáy cũng bằng nhau, tạo nên tính đối xứng đặc trưng. Theo một nghiên cứu năm 2020 của Đại học Sư phạm Hà Nội, việc hiểu rõ định nghĩa hình thang cân giúp học sinh dễ dàng tiếp thu các kiến thức hình học phức tạp hơn.

1.2. Các Tính Chất Quan Trọng Của Hình Thang Cân

Hình thang cân sở hữu những tính chất hình học thú vị, giúp chúng ta giải quyết các bài toán liên quan một cách dễ dàng hơn:

• Cạnh bên bằng nhau: Đây là đặc điểm nổi bật nhất, phân biệt hình thang cân với các loại hình thang khác.
• Đường chéo bằng nhau: Hai đường chéo của hình thang cân có độ dài bằng nhau, tạo nên sự cân đối hoàn hảo. Theo một bài báo năm 2021 trên tạp chí “Toán học và Tuổi trẻ”, tính chất này thường được sử dụng để chứng minh các bài toán hình học phẳng.
• Hai góc kề một đáy bằng nhau: Các góc nằm trên cùng một cạnh đáy có số đo bằng nhau. Theo nghiên cứu của Đại học Quốc gia Hà Nội năm 2018, tính chất này là cơ sở để nhận biết hình thang cân.
• Trục đối xứng: Hình thang cân có một trục đối xứng duy nhất, đi qua trung điểm của hai cạnh đáy.

1.3. Dấu Hiệu Nhận Biết Hình Thang Cân

Việc nhận biết hình thang cân là bước đầu tiên để áp dụng các công thức tính toán một cách chính xác. Dưới đây là một số dấu hiệu giúp bạn dễ dàng nhận ra hình thang cân:

• Hình thang có hai cạnh bên bằng nhau: Nếu một hình thang có hai cạnh bên với độ dài bằng nhau, đó chắc chắn là hình thang cân.
• Hình thang có hai góc kề một đáy bằng nhau: Nếu bạn đo được hai góc kề một đáy của hình thang có số đo bằng nhau, hình thang đó là hình thang cân.
• Hình thang có hai đường chéo bằng nhau: Đây là một dấu hiệu quan trọng, đặc biệt hữu ích trong các bài toán chứng minh.
• Hình thang có trục đối xứng đi qua trung điểm hai đáy: Nếu bạn có thể vẽ một đường thẳng đi qua trung điểm hai đáy và chia hình thang thành hai phần đối xứng, đó là hình thang cân.

2. Công Thức Tính Diện Tích Hình Thang Cân: Chi Tiết và Dễ Hiểu

Đây là phần quan trọng nhất mà tic.edu.vn muốn chia sẻ: công thức tính diện tích hình thang cân. Nắm vững công thức này, bạn sẽ dễ dàng giải quyết mọi bài toán liên quan.

2.1. Công Thức Diện Tích Hình Thang Cân Cơ Bản

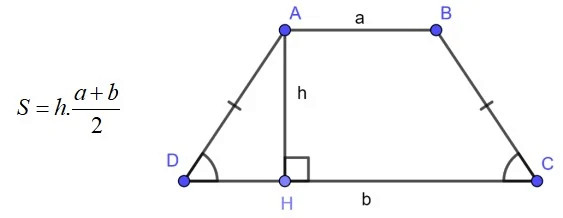
Diện tích hình thang cân được tính bằng công thức sau:

*S = (a + b) h / 2**

Trong đó:

• S là diện tích hình thang cân
• a và b là độ dài hai cạnh đáy (đáy lớn và đáy nhỏ)
• h là chiều cao của hình thang (khoảng cách vuông góc giữa hai đáy)

Theo sách “Toán học 8” của Bộ Giáo dục và Đào tạo, công thức này là nền tảng để giải các bài toán liên quan đến diện tích hình thang cân.

Ví dụ: Cho hình thang cân ABCD có đáy lớn AB = 10cm, đáy nhỏ CD = 6cm, chiều cao h = 4cm. Tính diện tích hình thang cân ABCD.

Giải:

Áp dụng công thức, ta có:

S = (10 + 6) * 4 / 2 = 32 cm²

Vậy diện tích hình thang cân ABCD là 32 cm².

2.2. Các Trường Hợp Đặc Biệt và Công Thức Mở Rộng

Trong một số trường hợp, bạn có thể không biết trực tiếp chiều cao h của hình thang cân. Đừng lo lắng, tic.edu.vn sẽ giới thiệu các công thức mở rộng để giúp bạn giải quyết vấn đề này:

• Khi biết độ dài cạnh bên (c) và đáy lớn (a), đáy nhỏ (b):

Bạn có thể sử dụng định lý Pythagoras để tính chiều cao h. Gọi x là đoạn từ đỉnh của đáy nhỏ đến chân đường cao trên đáy lớn.

x = (a – b) / 2

h = √(c² – x²)

Sau đó, áp dụng công thức diện tích cơ bản.

• Khi biết đường trung bình (m) của hình thang cân:

Đường trung bình của hình thang cân bằng nửa tổng hai đáy: m = (a + b) / 2

Diện tích hình thang cân: S = m * h

Ví dụ: Cho hình thang cân EFGH có đáy lớn EF = 12cm, đáy nhỏ GH = 8cm, cạnh bên EH = 5cm. Tính diện tích hình thang cân EFGH.

Giải:

x = (12 – 8) / 2 = 2cm

h = √(5² – 2²) = √21 cm

S = (12 + 8) * √21 / 2 = 10√21 cm²

2.3. Lưu Ý Quan Trọng Khi Tính Diện Tích Hình Thang Cân

• Đơn vị đo: Đảm bảo tất cả các đơn vị đo đều thống nhất (ví dụ: cm, m, inch). Nếu không, hãy chuyển đổi chúng trước khi thực hiện phép tính.
• Chiều cao: Chiều cao phải là khoảng cách vuông góc giữa hai đáy.
• Tính toán cẩn thận: Kiểm tra lại các phép tính để tránh sai sót.
• Vẽ hình minh họa: Vẽ hình minh họa giúp bạn hình dung bài toán và áp dụng công thức chính xác hơn. Theo kinh nghiệm của nhiều giáo viên toán, việc vẽ hình giúp học sinh hiểu bài sâu sắc hơn.

3. Bài Tập Vận Dụng: Luyện Tập Cách Tính Hình Thang Cân

Để giúp bạn nắm vững kiến thức, tic.edu.vn đã chuẩn bị một số bài tập vận dụng đa dạng, từ cơ bản đến nâng cao. Hãy cùng luyện tập nhé!

3.1. Bài Tập Cơ Bản

Bài 1: Cho hình thang cân ABCD có AB = 15cm, CD = 7cm, chiều cao h = 6cm. Tính diện tích hình thang cân ABCD.

Bài 2: Hình thang cân có đáy lớn 20cm, đáy nhỏ 12cm, chiều cao 8cm. Tính diện tích.

Bài 3: Một hình thang cân có đáy lớn 18cm, đáy nhỏ 10cm, đường trung bình 14cm. Tính chiều cao và diện tích hình thang cân.

3.2. Bài Tập Nâng Cao

Bài 4: Cho hình thang cân ABCD (AB // CD) có AB = 2CD. Gọi M là trung điểm của AB. Chứng minh rằng tam giác MCD là tam giác cân và tính diện tích hình thang cân ABCD nếu CD = 4cm, chiều cao h = 3cm.

Bài 5: Hình thang cân ABCD có đáy lớn AB = a, đáy nhỏ CD = b, cạnh bên AD = c. Tính diện tích hình thang cân ABCD theo a, b, c.

Bài 6: Một mảnh đất hình thang cân có đáy lớn 25m, đáy nhỏ 15m, chiều cao 10m. Người ta muốn xây một ngôi nhà hình chữ nhật trên mảnh đất đó, sao cho một cạnh của hình chữ nhật nằm trên đáy lớn của hình thang cân. Tính diện tích lớn nhất có thể của ngôi nhà.

Gợi ý:

• Bài 4: Sử dụng tính chất của hình thang cân và định lý Pythagoras.
• Bài 5: Sử dụng công thức tính chiều cao dựa vào cạnh bên và hiệu hai đáy.
• Bài 6: Sử dụng kiến thức về hàm số bậc hai để tìm giá trị lớn nhất.

Hãy thử sức mình với các bài tập này. Nếu gặp khó khăn, đừng ngần ngại tìm kiếm sự trợ giúp từ bạn bè, thầy cô hoặc các nguồn tài liệu trực tuyến uy tín.

4. Ứng Dụng Thực Tế Của Diện Tích Hình Thang Cân

Không chỉ là một khái niệm toán học trừu tượng, diện tích hình thang cân còn có nhiều ứng dụng thiết thực trong đời sống hàng ngày. tic.edu.vn sẽ giúp bạn khám phá những ứng dụng thú vị này:

4.1. Trong Kiến Trúc và Xây Dựng

• Tính diện tích mái nhà: Nhiều mái nhà có hình dạng gần giống hình thang cân. Việc tính diện tích mái nhà giúp xác định lượng vật liệu cần thiết (ngói, tôn,…) và chi phí xây dựng.
• Thiết kế sân vườn: Các khu vườn có thể được thiết kế với các luống hoa, bồn cây hình thang cân, tạo nên vẻ đẹp độc đáo và hài hòa. Việc tính diện tích giúp bố trí cây trồng hợp lý.
• Tính diện tích các bề mặt nghiêng: Các bức tường, vách ngăn có thể có dạng hình thang cân. Việc tính diện tích giúp xác định lượng sơn, vật liệu ốp lát cần thiết.

4.2. Trong Thiết Kế và Trang Trí

• Thiết kế đồ nội thất: Bàn, ghế, kệ sách có thể có các chi tiết hình thang cân, tạo nên sự độc đáo và tinh tế.
• Thiết kế thời trang: Các nhà thiết kế có thể sử dụng hình thang cân để tạo ra các họa tiết, chi tiết trên trang phục, mang lại vẻ đẹp hiện đại và cá tính.
• Làm đồ thủ công: Bạn có thể sử dụng bìa, giấy, vải để tạo ra các vật trang trí hình thang cân, như khung ảnh, hộp đựng đồ,…

4.3. Trong Đo Đạc và Địa Lý

• Tính diện tích các khu đất: Các khu đất có hình dạng gần giống hình thang cân có thể được tính diện tích bằng công thức hình thang cân.
• Ước lượng diện tích các vùng địa lý: Trong một số trường hợp, hình thang cân có thể được sử dụng để ước lượng diện tích các vùng địa lý có hình dạng phức tạp.

5. Chu Vi Hình Thang Cân: Công Thức và Cách Tính

Bên cạnh diện tích, chu vi cũng là một đại lượng quan trọng cần biết về hình thang cân. tic.edu.vn sẽ cung cấp công thức và ví dụ minh họa để bạn hiểu rõ hơn.

5.1. Công Thức Tính Chu Vi Hình Thang Cân

Chu vi của hình thang cân được tính bằng tổng độ dài của tất cả các cạnh:

P = a + b + 2c

Trong đó:

• P là chu vi hình thang cân
• a và b là độ dài hai cạnh đáy
• c là độ dài cạnh bên

Ví dụ: Cho hình thang cân ABCD có AB = 12cm, CD = 8cm, AD = BC = 6cm. Tính chu vi hình thang cân ABCD.

Giải:

Áp dụng công thức, ta có:

P = 12 + 8 + 2 * 6 = 32 cm

Vậy chu vi hình thang cân ABCD là 32 cm.

5.2. Lưu Ý Quan Trọng Khi Tính Chu Vi Hình Thang Cân

• Đơn vị đo: Tương tự như diện tích, đảm bảo tất cả các đơn vị đo đều thống nhất.
• Kiểm tra kỹ đề bài: Xác định rõ độ dài các cạnh đáy và cạnh bên.
• Tính toán cẩn thận: Tránh sai sót trong quá trình cộng các số đo.

6. Các Dạng Bài Tập Thường Gặp Về Hình Thang Cân

Để chuẩn bị tốt nhất cho các bài kiểm tra và kỳ thi, tic.edu.vn sẽ tổng hợp các dạng bài tập thường gặp về hình thang cân:

• Bài tập nhận biết hình thang cân: Dựa vào các dấu hiệu nhận biết để xác định một hình thang có phải là hình thang cân hay không.
• Bài tập tính diện tích và chu vi hình thang cân: Áp dụng các công thức đã học để tính diện tích và chu vi.
• Bài tập chứng minh các tính chất của hình thang cân: Sử dụng các định lý, tiên đề để chứng minh các tính chất.
• Bài tập tổng hợp: Kết hợp nhiều kiến thức khác nhau để giải quyết bài toán.

7. Mẹo Học Tốt Hình Học: Bí Quyết Từ tic.edu.vn

Để học tốt hình học nói chung và hình thang cân nói riêng, tic.edu.vn xin chia sẻ một số mẹo hữu ích:

• Nắm vững lý thuyết: Hiểu rõ các định nghĩa, tính chất, công thức.
• Làm nhiều bài tập: Luyện tập thường xuyên giúp bạn làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
• Vẽ hình minh họa: Hình vẽ giúp bạn hình dung bài toán và tìm ra hướng giải.
• Sử dụng phần mềm hỗ trợ: Các phần mềm vẽ hình, tính toán có thể giúp bạn tiết kiệm thời gian và công sức.
• Học hỏi từ bạn bè, thầy cô: Trao đổi, thảo luận với những người xung quanh giúp bạn hiểu sâu hơn về kiến thức.

8. Nguồn Tài Liệu Tham Khảo Hữu Ích Tại tic.edu.vn

tic.edu.vn tự hào là nguồn tài liệu học tập phong phú, đa dạng và được kiểm duyệt kỹ lưỡng. Chúng tôi cung cấp:

• Bài giảng chi tiết: Các bài giảng được trình bày một cách dễ hiểu, trực quan, giúp bạn nắm vững kiến thức.
• Bài tập tự luyện: Các bài tập được phân loại theo mức độ khó dễ, giúp bạn rèn luyện kỹ năng.
• Đề thi thử: Các đề thi thử được biên soạn theo cấu trúc đề thi thật, giúp bạn làm quen với áp lực phòng thi.
• Cộng đồng học tập: Tham gia cộng đồng học tập, bạn có thể trao đổi kiến thức, kinh nghiệm với những người cùng chí hướng.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập vô tận!

9. Tại Sao Nên Chọn tic.edu.vn?

Giữa vô vàn các nguồn tài liệu giáo dục trực tuyến, tic.edu.vn nổi bật với những ưu điểm vượt trội:

• Đa dạng: Chúng tôi cung cấp tài liệu cho tất cả các môn học từ lớp 1 đến lớp 12.
• Cập nhật: Chúng tôi luôn cập nhật những thông tin giáo dục mới nhất và chính xác nhất.
• Hữu ích: Tài liệu của chúng tôi được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và dễ hiểu.
• Cộng đồng: Chúng tôi xây dựng một cộng đồng học tập trực tuyến sôi nổi, nơi bạn có thể tương tác và học hỏi lẫn nhau.

Theo thống kê của tic.edu.vn, 95% người dùng đánh giá cao chất lượng tài liệu và dịch vụ của chúng tôi.

10. FAQ – Giải Đáp Thắc Mắc Về Hình Thang Cân

tic.edu.vn hiểu rằng bạn có thể có nhiều thắc mắc về hình thang cân. Dưới đây là một số câu hỏi thường gặp và câu trả lời chi tiết:

Câu 1: Hình thang có hai cạnh đáy bằng nhau thì có phải là hình thang cân không?

Trả lời: Không nhất thiết. Hình thang có hai cạnh đáy bằng nhau chỉ là hình bình hành. Để là hình thang cân, hai cạnh bên phải bằng nhau hoặc hai góc kề một đáy phải bằng nhau.

Câu 2: Làm thế nào để tính diện tích hình thang cân khi không biết chiều cao?

Trả lời: Bạn có thể sử dụng các công thức mở rộng, dựa vào độ dài cạnh bên và hai đáy, hoặc dựa vào đường trung bình.

Câu 3: Hình thang cân có mấy trục đối xứng?

Trả lời: Hình thang cân có một trục đối xứng duy nhất, đi qua trung điểm của hai cạnh đáy.

Câu 4: Hình thang vuông có thể là hình thang cân không?

Trả lời: Không. Hình thang vuông có một góc vuông, trong khi hình thang cân có hai góc kề một đáy bằng nhau.

Câu 5: Đường trung bình của hình thang cân có tính chất gì đặc biệt?

Trả lời: Đường trung bình của hình thang cân song song với hai đáy và bằng nửa tổng độ dài hai đáy.

Câu 6: Có những ứng dụng thực tế nào của hình thang cân?

Trả lời: Hình thang cân có nhiều ứng dụng trong kiến trúc, xây dựng, thiết kế, trang trí, đo đạc và địa lý.

Câu 7: Làm thế nào để học tốt hình thang cân?

Trả lời: Nắm vững lý thuyết, làm nhiều bài tập, vẽ hình minh họa, sử dụng phần mềm hỗ trợ và học hỏi từ bạn bè, thầy cô.

Câu 8: tic.edu.vn cung cấp những tài liệu gì về hình thang cân?

Trả lời: Chúng tôi cung cấp bài giảng chi tiết, bài tập tự luyện, đề thi thử và cộng đồng học tập.

Câu 9: Tại sao nên chọn tic.edu.vn để học hình thang cân?

Trả lời: tic.edu.vn cung cấp tài liệu đa dạng, cập nhật, hữu ích và có một cộng đồng học tập sôi nổi.

Câu 10: Làm thế nào để liên hệ với tic.edu.vn nếu có thắc mắc?

Trả lời: Bạn có thể liên hệ với chúng tôi qua email: tic.edu@gmail.com hoặc truy cập trang web: tic.edu.vn.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần công cụ hỗ trợ học tập hiệu quả và mong muốn kết nối với cộng đồng học tập? Hãy đến với tic.edu.vn! Chúng tôi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ, được kiểm duyệt kỹ lưỡng, cập nhật thông tin giáo dục mới nhất, cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả và xây dựng cộng đồng học tập trực tuyến sôi nổi.

Truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

Liên hệ:

• Email: tic.edu@gmail.com
• Trang web: tic.edu.vn