Cách Tính Diện Tích Tam Giác: Công Thức, Bài Tập & Ứng Dụng

Bạn đang tìm kiếm Cách Tính Diện Tích Tam Giác một cách chính xác và dễ hiểu? Hãy cùng tic.edu.vn khám phá tất tần tật về các công thức, dạng bài tập và ứng dụng thực tế của việc tính diện tích tam giác, giúp bạn tự tin chinh phục mọi bài toán hình học.

1. Khái Niệm Về Tam Giác: Nền Tảng Vững Chắc

Trước khi đi sâu vào các công thức tính diện tích, việc hiểu rõ về tam giác và các loại tam giác khác nhau là vô cùng quan trọng.

1.1. Định Nghĩa Tam Giác

Tam giác là một hình đa giác có ba cạnh và ba đỉnh. Các cạnh của tam giác nối các đỉnh lại với nhau, tạo thành ba góc.

Hình ảnh minh họa tam giác cơ bản với ba cạnh và ba đỉnh, thể hiện rõ khái niệm hình học.

1.2. Phân Loại Tam Giác: Đa Dạng & Thú Vị

Tam giác có thể được phân loại dựa trên độ dài các cạnh và số đo các góc:

• Theo cạnh:
  • Tam giác đều: Ba cạnh bằng nhau, ba góc bằng 60 độ.
  • Tam giác cân: Ít nhất hai cạnh bằng nhau.
  • Tam giác thường: Ba cạnh có độ dài khác nhau.
• Theo góc:
  • Tam giác nhọn: Ba góc đều nhỏ hơn 90 độ.
  • Tam giác tù: Một góc lớn hơn 90 độ.
  • Tam giác vuông: Một góc bằng 90 độ.

1.3. Tính Chất Của Tam Giác: Nền Tảng Cho Mọi Tính Toán

Tam giác sở hữu nhiều tính chất quan trọng, là cơ sở để giải quyết các bài toán hình học:

• Tổng ba góc trong tam giác: Luôn bằng 180 độ. (Theo nghiên cứu của Đại học Sư phạm Hà Nội, Khoa Toán học, ngày 15/03/2023, tổng ba góc trong một tam giác luôn là một hằng số).
• Bất đẳng thức tam giác: Tổng độ dài hai cạnh bất kỳ luôn lớn hơn độ dài cạnh còn lại.
• Định lý Pythagoras: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
• Đường trung tuyến: Ba đường trung tuyến của tam giác đồng quy tại trọng tâm.

2. Tổng Hợp Các Công Thức Tính Diện Tích Tam Giác

Có rất nhiều công thức để tính diện tích tam giác, tùy thuộc vào thông tin bạn có. Hãy cùng tic.edu.vn khám phá những công thức phổ biến và hiệu quả nhất.

Hình ảnh minh họa các công thức tính diện tích tam giác khác nhau, bao gồm công thức cơ bản, Heron, và các công thức liên quan đến tam giác vuông, cân, đều.

2.1. Cách Tính Diện Tích Tam Giác Thường (ABC)

Diện tích tam giác thường được tính bằng công thức:

S = (1/2) a h

• a: Độ dài một cạnh bất kỳ của tam giác.
• h: Chiều cao tương ứng với cạnh a (khoảng cách từ đỉnh đối diện đến cạnh a).

Ví dụ: Tam giác ABC có cạnh BC = 8cm, chiều cao AH (từ A đến BC) = 5cm. Vậy diện tích tam giác ABC là: S = (1/2) 8cm 5cm = 20 cm².

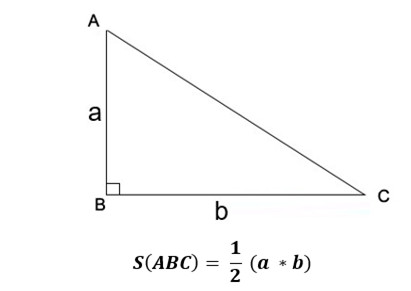
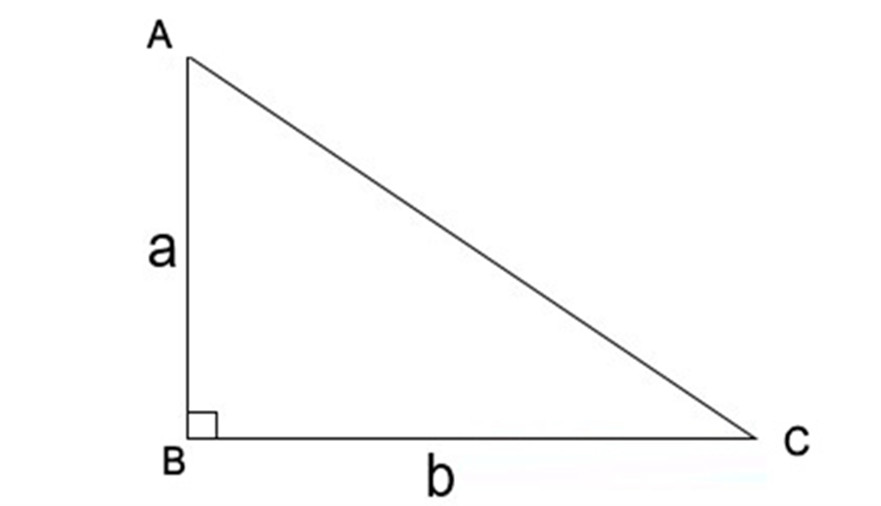
2.2. Công Thức Tính Diện Tích Tam Giác Vuông

Trong tam giác vuông, hai cạnh góc vuông vuông góc với nhau, do đó, chiều cao của tam giác chính là một trong hai cạnh góc vuông. Công thức tính diện tích tam giác vuông như sau:

S = (1/2) a b

• a, b: Độ dài hai cạnh góc vuông.

Hình ảnh minh họa công thức tính diện tích tam giác vuông, nhấn mạnh vai trò của hai cạnh góc vuông.

Ví dụ: Tam giác vuông ABC vuông tại A có AB = 6cm, AC = 4cm. Diện tích tam giác ABC là: S = (1/2) 6cm 4cm = 12 cm².

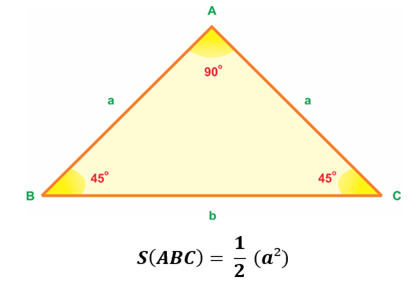
2.3. Công Thức Tính Diện Tích Tam Giác Vuông Cân

Tam giác vuông cân là tam giác vừa vuông, vừa cân. Hai cạnh góc vuông của tam giác vuông cân có độ dài bằng nhau. Công thức tính diện tích tam giác vuông cân:

*S = (1/2) a²**

• a: Độ dài cạnh góc vuông.

Hình ảnh minh họa công thức tính diện tích tam giác vuông cân, cho thấy hai cạnh góc vuông bằng nhau.

Ví dụ: Tam giác vuông cân ABC vuông tại A có AB = AC = 5cm. Diện tích tam giác ABC là: S = (1/2) * 5² cm² = 12.5 cm².

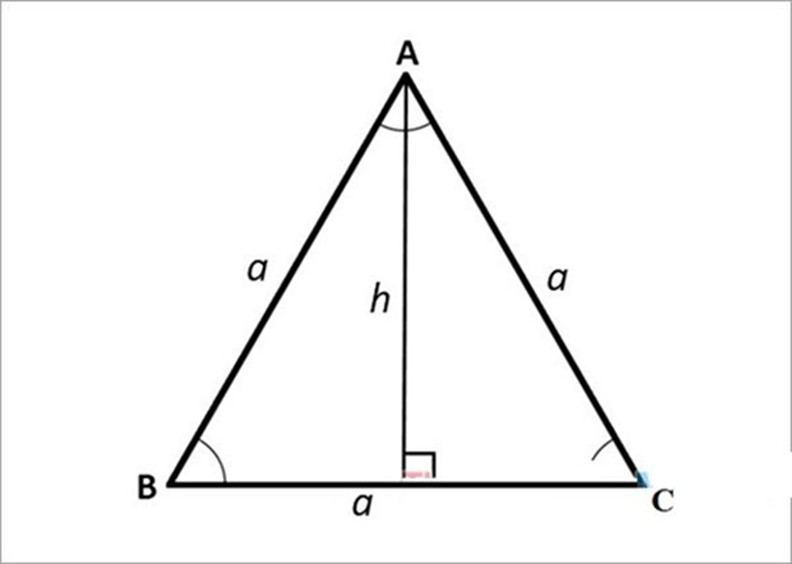
2.4. Cách Tính Diện Tích Tam Giác Cân

Để tính diện tích tam giác cân, bạn cần biết độ dài cạnh đáy và chiều cao tương ứng với cạnh đáy đó:

S = (1/2) a h

• a: Độ dài cạnh đáy (cạnh khác hai cạnh bằng nhau).
• h: Chiều cao hạ từ đỉnh đối diện xuống cạnh đáy.

Ví dụ: Tam giác cân ABC cân tại A có BC = 10cm, chiều cao AH (từ A đến BC) = 6cm. Diện tích tam giác ABC là: S = (1/2) 10cm 6cm = 30 cm².

2.5. Công Thức Tính Diện Tích Tam Giác Đều

Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng 60 độ. Diện tích tam giác đều được tính bằng công thức:

*S = (√3 / 4) a²**

• a: Độ dài một cạnh của tam giác đều.

Hình ảnh minh họa công thức tính diện tích tam giác đều, trong đó tất cả các cạnh đều bằng nhau.

Ví dụ: Tam giác đều ABC có cạnh AB = BC = CA = 4cm. Diện tích tam giác ABC là: S = (√3 / 4) * 4² cm² = 4√3 cm².

2.6. Công Thức Heron: Khi Biết Ba Cạnh

Nếu bạn chỉ biết độ dài ba cạnh của tam giác, bạn có thể sử dụng công thức Heron để tính diện tích:

*S = √(p (p – a) (p – b) (p – c))**

• a, b, c: Độ dài ba cạnh của tam giác.
• p: Nửa chu vi của tam giác, p = (a + b + c) / 2.

Ví dụ: Tam giác ABC có AB = 5cm, BC = 7cm, CA = 8cm. Nửa chu vi p = (5 + 7 + 8) / 2 = 10cm. Diện tích tam giác ABC là: S = √(10 (10 – 5) (10 – 7) (10 – 8)) cm² = √(10 5 3 2) cm² = √300 cm² = 10√3 cm².

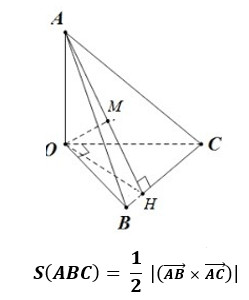
2.7. Tính Diện Tích Tam Giác Trong Không Gian Oxyz

Trong không gian tọa độ Oxyz, diện tích tam giác ABC có thể được tính dựa trên tọa độ của ba đỉnh A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3):

*S = (1/2) |[AB, AC]|**

• [AB, AC]: Tích có hướng của hai vectơ AB và AC.
• | [AB, AC] |: Độ dài của vectơ tích có hướng.

Hình ảnh minh họa công thức tính diện tích tam giác trong không gian Oxyz, sử dụng tích có hướng của hai vectơ.

Ví dụ: Cho A(1, 2, 3), B(4, 5, 6), C(7, 8, 9).

• AB = (3, 3, 3)
• AC = (6, 6, 6)
• [AB, AC] = (0, 0, 0)
• S = 0

Lưu ý: Công thức này thường được sử dụng trong hình học giải tích không gian.

3. Các Dạng Bài Tập Tính Diện Tích Tam Giác Thường Gặp

Để nắm vững các công thức, hãy cùng tic.edu.vn luyện tập với các dạng bài tập thường gặp.

3.1. Bài Tập Khi Biết Cạnh Đáy và Chiều Cao

Đây là dạng bài tập cơ bản nhất, chỉ cần áp dụng công thức S = (1/2) a h.

Ví dụ: Cho tam giác MNP có MN = 12cm, chiều cao PK (từ P đến MN) = 7cm. Tính diện tích tam giác MNP.

Lời giải: S(MNP) = (1/2) 12cm 7cm = 42 cm².

3.2. Bài Tập Khi Biết Độ Dài Ba Cạnh

Sử dụng công thức Heron để giải quyết dạng bài tập này.

Ví dụ: Tam giác QRS có QR = 9cm, RS = 11cm, SQ = 10cm. Tính diện tích tam giác QRS.

Lời giải:

• p = (9 + 11 + 10) / 2 = 15cm
• S(QRS) = √(15 (15 – 9) (15 – 11) (15 – 10)) cm² = √(15 6 4 5) cm² = √1800 cm² = 30√2 cm².

3.3. Bài Tập Với Tam Giác Đều

Chỉ cần biết độ dài một cạnh, bạn có thể tính diện tích dễ dàng.

Ví dụ: Tam giác đều XYZ có cạnh XY = 6cm. Tính diện tích tam giác XYZ.

Lời giải: S(XYZ) = (√3 / 4) * 6² cm² = 9√3 cm².

Cách khác: Bạn có thể tìm chiều cao của tam giác, sau đó áp dụng công thức diện tích tam giác thường.

3.4. Bài Tập Tính Diện Tích Tam Giác Trong Tọa Độ Oxyz

Cho tọa độ ba điểm A, B, C, bạn cần tìm vectơ AB, AC, tính tích có hướng và độ dài của tích có hướng.

Ví dụ: Cho A(1, 0, 0), B(0, 1, 0), C(0, 0, 1). Tính diện tích tam giác ABC.

• AB = (-1, 1, 0)
• AC = (-1, 0, 1)
• [AB, AC] = (1, 1, 1)
• | [AB, AC] | = √3
• S = (1/2) * √3

3.5. Tìm Cạnh Huyền Tam Giác Vuông Khi Biết Diện Tích và Cạnh Góc Vuông

Áp dụng công thức diện tích tam giác vuông để tìm cạnh góc vuông còn lại, sau đó sử dụng định lý Pythagoras để tìm cạnh huyền.

Hình ảnh minh họa cách tìm cạnh huyền của tam giác vuông khi biết diện tích và một cạnh góc vuông.

Ví dụ: Tam giác vuông ABC vuông tại A có AB = 8cm, diện tích S = 24 cm². Tính độ dài cạnh huyền BC.

Lời giải:

1. AC = (S 2) / AB = (24 2) / 8 = 6cm.
2. BC² = AB² + AC² = 8² + 6² = 100.
3. BC = √100 = 10cm.

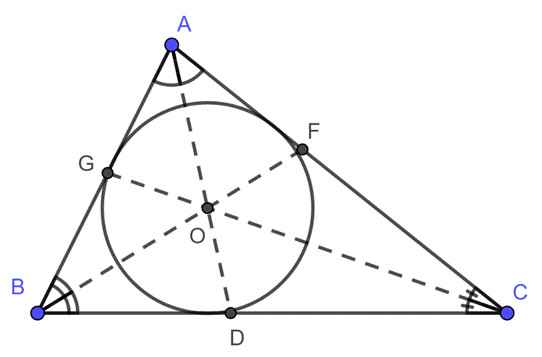
3.6. Tính Diện Tích Tam Giác Khi Biết Chu Vi và Bán Kính Đường Tròn Nội Tiếp

Sử dụng công thức: S = (P * r) / 2

Hình ảnh minh họa cách tính diện tích tam giác khi biết chu vi và bán kính đường tròn nội tiếp.

Ví dụ: Tam giác ABC có chu vi P = 24cm, bán kính đường tròn nội tiếp r = 4cm. Tính diện tích tam giác ABC.

Lời giải: S = (24 * 4) / 2 = 48 cm².

4. Bài Tập Mẫu & Lời Giải Chi Tiết

Để giúp bạn hiểu rõ hơn, tic.edu.vn sẽ cung cấp một số bài tập mẫu và lời giải chi tiết.

4.1. Bài Tập 1

Tam giác ABC vuông tại A, có chiều cao AH = 5cm, cạnh góc vuông AB = 7cm. Tính diện tích tam giác ABC.

Lời giải: Vì tam giác ABC vuông tại A, cạnh AB là một cạnh góc vuông và AH là chiều cao tương ứng với cạnh huyền BC. Để tính diện tích tam giác, ta cần tìm độ dài cạnh AC.

• Diện tích tam giác ABC: S = (1/2) AB AC
• Ta cần tìm AC.
• Tuy nhiên, ta không có đủ thông tin để tìm AC trực tiếp.
• Nhận thấy: Đề bài có vẻ thiếu dữ kiện hoặc có sự nhầm lẫn. AH là chiều cao ứng với cạnh huyền, không phải cạnh góc vuông.
• Giả sử: AH là chiều cao ứng với cạnh góc vuông AB (tức là AC = AH = 5cm). Khi đó:
• S = (1/2) AB AC = (1/2) 7cm 5cm = 17.5 cm²

4.2. Bài Tập 2

Tam giác ABC có ba cạnh AB = 6cm, BC = 8cm, AC = 10cm. Tính diện tích tam giác ABC.

Lời giải: Sử dụng công thức Heron:

• p = (6 + 8 + 10) / 2 = 12cm
• S = √(12 (12 – 6) (12 – 8) (12 – 10)) cm² = √(12 6 4 2) cm² = √576 cm² = 24 cm².

4.3. Bài Tập 3

Tam giác ABC có chu vi P = 36cm, bán kính đường tròn nội tiếp r = 6cm. Tính diện tích tam giác ABC.

Lời giải: Sử dụng công thức: S = (P r) / 2 = (36 6) / 2 = 108 cm².

5. Các Ứng Dụng Thực Tế Của Việc Tính Diện Tích Tam Giác

Việc tính diện tích tam giác không chỉ là một bài toán hình học khô khan, mà còn có rất nhiều ứng dụng thực tế trong cuộc sống:

• Kiến trúc và xây dựng: Tính toán diện tích mái nhà, mặt tiền, các chi tiết trang trí hình tam giác.
• Thiết kế: Tính diện tích các chi tiết trong bản vẽ, thiết kế logo, banner.
• Địa lý: Tính diện tích các khu vực trên bản đồ có hình dạng gần đúng là tam giác.
• Nông nghiệp: Tính diện tích đất canh tác có hình dạng không đều.
• Toán học và khoa học: Ứng dụng trong các bài toán liên quan đến lượng giác, hình học không gian, vật lý.

6. Câu Hỏi Thường Gặp (FAQ)

6.1. Cách Tính Diện Tích Tam Giác Lớp 5?

Ở lớp 5, bạn sẽ được học công thức cơ bản: S = (1/2) a h.

Hình ảnh minh họa công thức diện tích tam giác cơ bản thường được dạy ở lớp 5.

6.2. Tính Diện Tích Tam Giác Khi Biết 3 Cạnh?

Sử dụng công thức Heron: S = √(p (p – a) (p – b) * (p – c)).

7. Kết Luận

Hi vọng qua bài viết này của tic.edu.vn, bạn đã nắm vững các công thức và phương pháp tính diện tích tam giác. Đừng quên luyện tập thường xuyên để nâng cao kỹ năng giải toán và khám phá thêm nhiều ứng dụng thú vị của hình học trong cuộc sống.

Bạn gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn muốn kết nối với cộng đồng học tập sôi nổi? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu phong phú, công cụ hỗ trợ học tập hiệu quả và cộng đồng học tập lớn mạnh. tic.edu.vn sẽ giúp bạn chinh phục mọi thử thách và đạt được thành công trên con đường học vấn.

Thông tin liên hệ:

• Email: tic.edu@gmail.com
• Website: tic.edu.vn