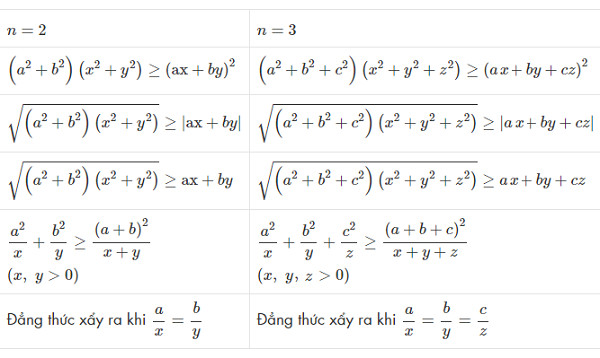
**Bất Đẳng Thức Bunhiacopxki: Định Nghĩa, Ứng Dụng và Bài Tập**

Bất đẳng Thức Bunhiacopxki, một công cụ mạnh mẽ trong toán học, giúp giải quyết các bài toán chứng minh bất đẳng thức và tìm cực trị một cách hiệu quả, đặc biệt là khi bạn tìm kiếm tài liệu chất lượng và đáng tin cậy tại tic.edu.vn. Chúng tôi cung cấp cho bạn một cái nhìn sâu sắc về bất đẳng thức Cauchy-Schwarz, công thức, cách chứng minh và các bài tập áp dụng, giúp bạn chinh phục những bài toán hóc búa nhất liên quan đến đánh giá biểu thức.

1. Bất Đẳng Thức Bunhiacopxki Là Gì?

Bất đẳng thức Bunhiacopxki, còn được biết đến với tên gọi bất đẳng thức Cauchy-Bunhiacopxki-Schwarz (sau này thường được rút gọn), là một công cụ toán học quan trọng. Vậy bất đẳng thức Bunhiacopxki phát biểu điều gì? Bất đẳng thức này được ứng dụng rộng rãi trong việc chứng minh các bất đẳng thức và tìm giá trị lớn nhất, nhỏ nhất (cực trị) của các biểu thức.

Bất đẳng thức Bunhiacopxki là một công cụ hữu ích trong toán học (Nguồn: Internet). Alt: Định nghĩa bất đẳng thức Bunhiacopxki và ứng dụng trong giải toán.

2. Công Thức Bất Đẳng Thức Bunhiacopxki

2.1. Dạng Cơ Bản

Công thức bất đẳng thức Bunhiacopxki dạng cơ bản nhất được biểu diễn như sau:

(a² + b²) (c² + d²) ≥ (ac + bd)²

Dấu “=” xảy ra khi và chỉ khi ad = bc hoặc a/c = b/d (với c, d khác 0).

2.2. Dạng Tổng Quát

Với hai bộ số thực (a₁, a₂,…, aₙ) và (b₁, b₂,…, bₙ), bất đẳng thức Bunhiacopxki có dạng tổng quát:

(a₁² + a₂² + … + aₙ²) (b₁² + b₂² + … + bₙ²) ≥ (a₁b₁ + a₂b₂ + … + aₙbₙ)²

Dấu “=” xảy ra khi và chỉ khi a₁/b₁ = a₂/b₂ = … = aₙ/bₙ (với bᵢ khác 0). Nếu tồn tại một số bᵢ = 0 thì số aᵢ tương ứng cũng phải bằng 0.

Bất đẳng thức Bunhiacopxki dạng tổng quát. Alt: Công thức tổng quát của bất đẳng thức Bunhiacopxki với n số và điều kiện dấu bằng xảy ra.

2.3. Mở Rộng Cho Tích Phân

Bất đẳng thức Bunhiacopxki còn có thể mở rộng cho tích phân:

[∫f(x)g(x)dx]² ≤ ∫f²(x)dx . ∫g²(x)dx

Trong đó, f(x) và g(x) là các hàm số khả tích trên một khoảng xác định.

3. Các Hệ Quả Quan Trọng Của Bất Đẳng Thức Bunhiacopxki

Bất đẳng thức Bunhiacopxki có nhiều hệ quả hữu ích, hỗ trợ giải quyết các bài toán liên quan đến tìm min, max:

3.1. Hệ Quả 1

Nếu a₁x₁ + a₂x₂ + … + aₙxₙ = C (C là hằng số) thì:

min(x₁² + x₂² + … + xₙ²) = C² / (a₁² + a₂² + … + aₙ²)

Đẳng thức xảy ra khi x₁/a₁ = x₂/a₂ = … = xₙ/aₙ

3.2. Hệ Quả 2

Nếu x₁² + x₂² + … + xₙ² = C² (C là hằng số) thì:

• Max(a₁x₁ + a₂x₂ + … + aₙxₙ) = C . √(a₁² + a₂² + … + aₙ²) , đạt được khi aᵢxᵢ ≥ 0 và a₁/x₁ = a₂/x₂ = … = aₙ/xₙ
• Min(a₁x₁ + a₂x₂ + … + aₙxₙ) = -C . √(a₁² + a₂² + … + aₙ²) , đạt được khi aᵢxᵢ ≤ 0 và a₁/x₁ = a₂/x₂ = … = aₙ/xₙ

4. Chứng Minh Bất Đẳng Thức Bunhiacopxki

Để chứng minh bất đẳng thức Bunhiacopxki dạng cơ bản, ta có thể thực hiện như sau:

(a² + b²) (c² + d²) ≥ (ac + bd)²

<=> (ac)² + (ad)² + (bc)² + (bd)² ≥ (ac)² + 2abcd + (bd)²

<=> (ad)² + (bc)² – 2abcd ≥ 0

<=> (ad – bc)² ≥ 0 (luôn đúng với mọi a, b, c, d thuộc R)

Vậy bất đẳng thức Bunhiacopxki được chứng minh. Dấu “=” xảy ra khi và chỉ khi ad = bc.

5. Ứng Dụng Bất Đẳng Thức Bunhiacopxki Trong Giải Toán

Bất đẳng thức Bunhiacopxki là một công cụ mạnh mẽ để giải quyết nhiều dạng bài toán khác nhau. Dưới đây là một số ứng dụng phổ biến:

5.1. Chứng Minh Bất Đẳng Thức

Bất đẳng thức Bunhiacopxki thường được sử dụng để chứng minh các bất đẳng thức phức tạp bằng cách biến đổi và áp dụng công thức một cách khéo léo.

5.2. Tìm Giá Trị Lớn Nhất (Max) và Giá Trị Nhỏ Nhất (Min)

Bất đẳng thức Bunhiacopxki giúp tìm cực trị của các biểu thức bằng cách đánh giá và chặn trên hoặc chặn dưới biểu thức đó.

5.3. Giải Các Bài Toán Liên Quan Đến Tích Vô Hướng

Trong hình học, bất đẳng thức Bunhiacopxki có thể được sử dụng để giải các bài toán liên quan đến tích vô hướng của hai vectơ.

5.4. Các Bài Toán Về Dãy Số và Hàm Số

Bất đẳng thức Bunhiacopxki có thể mở rộng và áp dụng trong các bài toán liên quan đến dãy số và hàm số để chứng minh tính chất hoặc tìm giới hạn.

6. Các Dạng Bài Tập Bất Đẳng Thức Bunhiacopxki Lớp 9 (Có Lời Giải Chi Tiết)

Để giúp các em học sinh lớp 9 làm quen và nắm vững cách áp dụng bất đẳng thức Bunhiacopxki, dưới đây là một số bài tập minh họa có lời giải chi tiết:

Bài tập 1: Cho a, b, c là các số thực dương. Chứng minh rằng:

√(a + b) / (a + b + c) + √(b + c) / (a + b + c) + √(c + a) / (a + b + c) ≤ √6

Hướng dẫn giải:

Áp dụng bất đẳng thức Bunhiacopxki cho bộ ba số (1, 1, 1) và (√(a + b) / (a + b + c), √(b + c) / (a + b + c), √(c + a) / (a + b + c)), ta có:

[1.√(a + b) / (a + b + c) + 1.√(b + c) / (a + b + c) + 1.√(c + a) / (a + b + c)]² ≤ (1² + 1² + 1²) . [(a + b) / (a + b + c) + (b + c) / (a + b + c) + (c + a) / (a + b + c)]

<=> [√(a + b) / (a + b + c) + √(b + c) / (a + b + c) + √(c + a) / (a + b + c)]² ≤ 3 . [2(a + b + c) / (a + b + c)] = 6

<=> √(a + b) / (a + b + c) + √(b + c) / (a + b + c) + √(c + a) / (a + b + c) ≤ √6 (điều phải chứng minh).

Dấu “=” xảy ra khi và chỉ khi a = b = c.

Bài tập 2: Tìm giá trị lớn nhất của biểu thức: P = √(x – 2) + √(4 – x)

Hướng dẫn giải:

Điều kiện: 2 ≤ x ≤ 4

Áp dụng bất đẳng thức Bunhiacopxki cho bộ hai số (1, 1) và (√(x – 2), √(4 – x)), ta có:

[1.√(x – 2) + 1.√(4 – x)]² ≤ (1² + 1²) . (x – 2 + 4 – x) = 2 . 2 = 4

=> P² ≤ 4

=> -2 ≤ P ≤ 2

Vậy Pmax = 2 khi và chỉ khi √(x – 2) = √(4 – x) <=> x – 2 = 4 – x <=> x = 3 (thỏa mãn điều kiện).

Bài tập 3: Cho a, b, c là các số thực dương tùy ý. Chứng minh rằng:

a²/ (b + c) + b²/ (c + a) + c²/ (a + b) ≥ (a + b + c) / 2

Hướng dẫn giải:

Áp dụng bất đẳng thức Bunhiacopxki cho hai bộ số (a, b, c) và (√(b + c), √(c + a), √(a + b)), ta có:

(a² / (b + c) + b² / (c + a) + c² / (a + b)) . [(b + c) + (c + a) + (a + b)] ≥ (a + b + c)²

=> (a² / (b + c) + b² / (c + a) + c² / (a + b)) . [2(a + b + c)] ≥ (a + b + c)²

=> a² / (b + c) + b² / (c + a) + c² / (a + b) ≥ (a + b + c) / 2 (điều phải chứng minh).

Đẳng thức xảy ra khi và chỉ khi a = b = c.

7. Lưu Ý Quan Trọng Khi Sử Dụng Bất Đẳng Thức Bunhiacopxki

• Điều Kiện Dấu Bằng: Luôn kiểm tra điều kiện để dấu bằng xảy ra, giúp xác định khi nào biểu thức đạt giá trị lớn nhất hoặc nhỏ nhất.
• Lựa Chọn Bộ Số Phù Hợp: Việc lựa chọn bộ số (a₁, a₂,…, aₙ) và (b₁, b₂,…, bₙ) phù hợp là yếu tố then chốt để áp dụng bất đẳng thức Bunhiacopxki hiệu quả.
• Biến Đổi Đại Số: Đôi khi, cần thực hiện các biến đổi đại số trước khi áp dụng bất đẳng thức Bunhiacopxki để đưa bài toán về dạng phù hợp.

8. Các Nguồn Tài Liệu Tham Khảo Bất Đẳng Thức Bunhiacopxki Uy Tín

Để tìm hiểu sâu hơn về bất đẳng thức Bunhiacopxki, bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa và sách tham khảo toán học: Các cuốn sách này cung cấp lý thuyết cơ bản và bài tập minh họa.
• Các diễn đàn và trang web toán học uy tín: Nơi bạn có thể trao đổi, học hỏi kinh nghiệm giải toán từ các thành viên khác.
• Các bài báo khoa học và tạp chí toán học: Cung cấp các kết quả nghiên cứu mới nhất về bất đẳng thức Bunhiacopxki và ứng dụng của nó.

9. Lời Khuyên Học Tập Và Luyện Tập Bất Đẳng Thức Bunhiacopxki

• Nắm Vững Lý Thuyết: Hiểu rõ định nghĩa, công thức và các hệ quả của bất đẳng thức Bunhiacopxki.
• Làm Nhiều Bài Tập: Luyện tập giải nhiều dạng bài tập khác nhau để rèn luyện kỹ năng áp dụng.
• Tham Gia Thảo Luận: Trao đổi, thảo luận với bạn bè và thầy cô để học hỏi kinh nghiệm và giải đáp thắc mắc.
• Tìm Tòi Các Ứng Dụng: Khám phá các ứng dụng của bất đẳng thức Bunhiacopxki trong các lĩnh vực khác nhau của toán học và khoa học.

10. FAQ – Các Câu Hỏi Thường Gặp Về Bất Đẳng Thức Bunhiacopxki

10.1. Bất đẳng thức Bunhiacopxki có những tên gọi nào khác?

Bất đẳng thức Bunhiacopxki còn được gọi là bất đẳng thức Cauchy-Schwarz hoặc bất đẳng thức Bunhiacopxki-Schwarz.

10.2. Điều kiện để áp dụng bất đẳng thức Bunhiacopxki là gì?

Bất đẳng thức Bunhiacopxki áp dụng cho các số thực hoặc số phức. Trong dạng tổng quát, nó áp dụng cho hai bộ số có cùng số lượng phần tử.

10.3. Làm thế nào để xác định khi nào nên sử dụng bất đẳng thức Bunhiacopxki?

Bạn nên sử dụng bất đẳng thức Bunhiacopxki khi gặp các bài toán chứng minh bất đẳng thức, tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức, đặc biệt khi biểu thức có dạng tổng của các bình phương hoặc tích.

10.4. Dấu bằng trong bất đẳng thức Bunhiacopxki xảy ra khi nào?

Trong dạng cơ bản, dấu bằng xảy ra khi ad = bc. Trong dạng tổng quát, dấu bằng xảy ra khi a₁/b₁ = a₂/b₂ = … = aₙ/bₙ (với bᵢ khác 0).

10.5. Có những lỗi sai nào thường gặp khi áp dụng bất đẳng thức Bunhiacopxki?

Một lỗi sai thường gặp là không kiểm tra điều kiện dấu bằng xảy ra, dẫn đến kết luận sai về giá trị lớn nhất hoặc nhỏ nhất.

10.6. Bất đẳng thức Bunhiacopxki có ứng dụng gì trong hình học?

Trong hình học, bất đẳng thức Bunhiacopxki có thể được sử dụng để chứng minh các bất đẳng thức về độ dài đoạn thẳng, diện tích, thể tích và giải các bài toán liên quan đến tích vô hướng của hai vectơ.

10.7. Bất đẳng thức Bunhiacopxki có thể mở rộng cho tích phân không?

Có, bất đẳng thức Bunhiacopxki có thể mở rộng cho tích phân, cho phép đánh giá các tích phân dựa trên tích phân của bình phương các hàm số.

10.8. Làm thế nào để luyện tập bất đẳng thức Bunhiacopxki hiệu quả?

Để luyện tập hiệu quả, bạn nên bắt đầu với các bài tập cơ bản, sau đó chuyển sang các bài tập phức tạp hơn. Tham gia các diễn đàn toán học và trao đổi với bạn bè cũng là một cách tốt để nâng cao kỹ năng.

10.9. Bất đẳng thức Bunhiacopxki có liên hệ gì với các bất đẳng thức khác?

Bất đẳng thức Bunhiacopxki là một trường hợp đặc biệt của bất đẳng thức Holder và có liên hệ mật thiết với bất đẳng thức Cauchy.

10.10. Tôi có thể tìm thêm tài liệu về bất đẳng thức Bunhiacopxki ở đâu?

Bạn có thể tìm thêm tài liệu trên tic.edu.vn, sách giáo khoa, sách tham khảo toán học, các diễn đàn toán học uy tín và các bài báo khoa học.

Bất đẳng thức Bunhiacopxki là một công cụ mạnh mẽ và hữu ích trong toán học, giúp giải quyết nhiều bài toán khác nhau. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và sâu sắc về bất đẳng thức Bunhiacopxki. Chúc các bạn học tốt và thành công!

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kỹ năng giải toán và chinh phục các bài toán hóc búa? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả. Chúng tôi cung cấp các tài liệu được kiểm duyệt kỹ càng, thông tin giáo dục mới nhất và chính xác, cùng một cộng đồng học tập sôi nổi để bạn có thể trao đổi kiến thức và kinh nghiệm. Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.