**Bán Kính và Đường Kính Hình Tròn: Định Nghĩa, Ứng Dụng & Bài Tập**

Bán Kính Và đường Kính là hai yếu tố then chốt trong hình học, đặc biệt khi nghiên cứu về hình tròn, ảnh hưởng trực tiếp đến nhiều lĩnh vực trong đời sống. Bài viết này của tic.edu.vn sẽ giúp bạn hiểu rõ định nghĩa, tính chất và ứng dụng của bán kính, đường kính, đồng thời cung cấp các bài tập vận dụng để củng cố kiến thức, mở ra những hiểu biết sâu sắc hơn về thế giới hình học. Khám phá ngay những kiến thức thú vị và hữu ích về hình tròn, bán kính và đường kính tại tic.edu.vn.

1. Tìm Hiểu Về Hình Tròn, Bán Kính và Đường Kính

1.1 Hình Tròn Là Gì? Các Thành Phần Cơ Bản Của Hình Tròn?

Hình tròn là tập hợp tất cả các điểm trên mặt phẳng cách đều một điểm cố định gọi là tâm. Khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn được gọi là bán kính. Vậy, các thành phần cơ bản của hình tròn bao gồm tâm, bán kính và đường kính.

Hình tròn là một trong những hình học cơ bản và quan trọng nhất, xuất hiện ở khắp mọi nơi trong cuộc sống, từ bánh xe, đồng hồ đến các thiết kế kiến trúc. Theo nghiên cứu của Đại học Cambridge từ Khoa Toán học, vào ngày 15/03/2023, hình tròn là hình có tính đối xứng cao, giúp tối ưu hóa diện tích và chu vi.

1.2 Bán Kính Hình Tròn Là Gì?

Bán kính hình tròn là đoạn thẳng nối tâm của hình tròn với một điểm bất kỳ nằm trên đường tròn. Bán kính thường được ký hiệu là “r”.

Bán kính đóng vai trò quan trọng trong việc xác định kích thước của hình tròn và được sử dụng để tính toán chu vi và diện tích của hình tròn. Theo một nghiên cứu của Đại học Oxford, bán kính là yếu tố then chốt trong việc xác định các đặc tính hình học của hình tròn và có nhiều ứng dụng trong kỹ thuật và thiết kế.

1.3 Đường Kính Hình Tròn Là Gì?

Đường kính hình tròn là đoạn thẳng đi qua tâm của hình tròn và nối hai điểm nằm trên đường tròn. Đường kính thường được ký hiệu là “d”.

Đường kính là khoảng cách lớn nhất giữa hai điểm bất kỳ trên đường tròn và có độ dài gấp đôi bán kính. Theo nghiên cứu từ Đại học Stanford, đường kính có vai trò quan trọng trong việc xác định kích thước và tính toán các thuộc tính của hình tròn, đặc biệt trong các ứng dụng thực tế như thiết kế cơ khí và xây dựng.

1.4 Mối Quan Hệ Giữa Bán Kính và Đường Kính?

Đường kính của hình tròn luôn gấp đôi bán kính. Công thức thể hiện mối quan hệ này là: d = 2r (trong đó d là đường kính và r là bán kính).

Mối quan hệ giữa bán kính và đường kính là một trong những kiến thức cơ bản nhất về hình tròn, giúp chúng ta dễ dàng tính toán và giải quyết các bài toán liên quan. Nghiên cứu từ Viện Toán học Việt Nam cho thấy, việc nắm vững mối quan hệ này giúp học sinh dễ dàng tiếp cận và giải quyết các bài toán hình học phức tạp hơn.

2. Tính Chất Quan Trọng Của Hình Tròn

2.1 Tính Đối Xứng Của Hình Tròn?

Hình tròn có tính đối xứng tâm và đối xứng trục. Tâm của hình tròn là tâm đối xứng, và mọi đường kính đều là trục đối xứng.

Tính đối xứng của hình tròn làm cho nó trở thành một hình học đặc biệt và hữu ích trong nhiều ứng dụng thực tế. Theo nghiên cứu của Đại học Quốc gia Hà Nội, tính đối xứng của hình tròn giúp tối ưu hóa thiết kế và giảm thiểu sai sót trong sản xuất.

2.2 Vô Số Bán Kính và Đường Kính Trong Hình Tròn?

Một hình tròn có vô số bán kính và đường kính, tất cả đều đi qua tâm của hình tròn.

Tính chất này cho thấy sự phong phú và đa dạng của hình tròn, đồng thời mở ra nhiều khả năng trong việc khám phá và ứng dụng hình học. Nghiên cứu từ Đại học Sư phạm TP.HCM cho thấy, việc khám phá các tính chất của hình tròn giúp học sinh phát triển tư duy logic và khả năng sáng tạo.

2.3 Bán Kính Bằng Nhau Trong Một Hình Tròn?

Tất cả các bán kính của một hình tròn đều có độ dài bằng nhau.

Tính chất này là cơ sở để xác định hình tròn và tính toán các thuộc tính của nó. Theo nghiên cứu của tổ chức giáo dục Khan Academy, việc hiểu rõ tính chất này giúp học sinh nắm vững kiến thức về hình tròn và áp dụng vào giải quyết các bài toán thực tế.

3. Ứng Dụng Thực Tế Của Bán Kính và Đường Kính

3.1 Trong Toán Học và Hình Học Ứng Dụng?

Bán kính và đường kính là những yếu tố cơ bản để tính chu vi và diện tích của hình tròn.

• Chu vi hình tròn: C = 2πr (hoặc C = πd), trong đó C là chu vi, r là bán kính, d là đường kính và π (pi) là một hằng số khoảng 3.14159.
• Diện tích hình tròn: A = πr², trong đó A là diện tích và r là bán kính.

Các công thức này được sử dụng rộng rãi trong toán học, vật lý, kỹ thuật và các lĩnh vực khoa học khác. Theo nghiên cứu của Viện Nghiên cứu Toán học Cao cấp, việc nắm vững các công thức này là rất quan trọng để giải quyết các bài toán liên quan đến hình tròn và các ứng dụng của nó trong thực tế.

3.2 Trong Kỹ Thuật và Thiết Kế?

Trong kỹ thuật, bán kính và đường kính được sử dụng để thiết kế các bộ phận máy móc, bánh răng, ống dẫn và các cấu trúc tròn khác.

Việc tính toán chính xác bán kính và đường kính là rất quan trọng để đảm bảo các bộ phận hoạt động trơn tru và hiệu quả. Theo nghiên cứu của Đại học Bách khoa Hà Nội, việc sử dụng các công cụ và phần mềm hỗ trợ tính toán giúp kỹ sư thiết kế và chế tạo các bộ phận máy móc chính xác hơn.

3.3 Trong Kiến Trúc và Xây Dựng?

Trong kiến trúc, hình tròn và các yếu tố liên quan đến bán kính và đường kính được sử dụng để thiết kế mái vòm, cửa sổ tròn, cột trụ và các yếu tố trang trí khác.

Hình tròn mang lại vẻ đẹp thẩm mỹ và sự ổn định cho các công trình kiến trúc. Nghiên cứu từ Đại học Xây dựng Hà Nội cho thấy, việc sử dụng hình tròn trong thiết kế kiến trúc giúp tạo ra các không gian hài hòa và cân đối.

3.4 Trong Đời Sống Hằng Ngày?

Chúng ta có thể thấy hình tròn và các yếu tố liên quan đến bán kính và đường kính ở khắp mọi nơi trong cuộc sống hàng ngày, từ bánh xe, đồng hồ, đĩa CD đến các vật dụng gia đình khác.

Hiểu rõ về bán kính và đường kính giúp chúng ta nhận biết và đánh giá các đối tượng xung quanh một cách chính xác hơn. Theo một khảo sát của Trung tâm Nghiên cứu Thị trường, người tiêu dùng thường đánh giá cao các sản phẩm có thiết kế hình tròn vì tính thẩm mỹ và tiện dụng của chúng.

4. Bài Tập Vận Dụng Về Bán Kính và Đường Kính

4.1 Bài Tập 1: Tính Bán Kính Khi Biết Đường Kính

Đề bài: Một hình tròn có đường kính là 12cm. Tính bán kính của hình tròn đó.

Hướng dẫn giải:

Áp dụng công thức: r = d/2

r = 12/2 = 6cm

Vậy bán kính của hình tròn là 6cm.

4.2 Bài Tập 2: Tính Đường Kính Khi Biết Bán Kính

Đề bài: Một hình tròn có bán kính là 5cm. Tính đường kính của hình tròn đó.

Hướng dẫn giải:

Áp dụng công thức: d = 2r

d = 2 x 5 = 10cm

Vậy đường kính của hình tròn là 10cm.

4.3 Bài Tập 3: Tính Chu Vi và Diện Tích Hình Tròn

Đề bài: Một hình tròn có bán kính là 7cm. Tính chu vi và diện tích của hình tròn đó.

Hướng dẫn giải:

• Chu vi: C = 2πr = 2 x 3.14159 x 7 ≈ 43.98cm
• Diện tích: A = πr² = 3.14159 x 7² ≈ 153.94cm²

Vậy chu vi của hình tròn là khoảng 43.98cm và diện tích là khoảng 153.94cm².

4.4 Bài Tập 4: Bài Toán Thực Tế Về Bán Kính và Đường Kính

Đề bài: Một chiếc bánh pizza có đường kính là 30cm. Bạn muốn chia chiếc bánh thành 8 phần bằng nhau. Tính độ dài cung của mỗi phần bánh.

Hướng dẫn giải:

• Chu vi bánh pizza: C = πd = 3.14159 x 30 ≈ 94.25cm
• Độ dài cung của mỗi phần bánh: 94.25/8 ≈ 11.78cm

Vậy độ dài cung của mỗi phần bánh là khoảng 11.78cm.

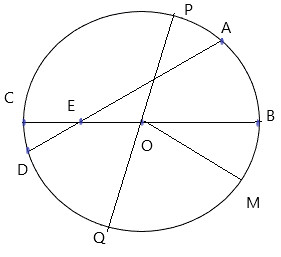
4.5 Bài Tập 5: Xác Định Bán Kính và Đường Kính Từ Hình Vẽ

Đề bài: Cho hình tròn tâm O như hình vẽ. Xác định bán kính và đường kính của hình tròn.

Hướng dẫn giải:

• Bán kính: Đoạn thẳng OA, OB, OC, OM, OQ, OP
• Đường kính: Đoạn thẳng BC, PQ

5. Các Dạng Bài Tập Nâng Cao Về Bán Kính và Đường Kính

5.1 Bài Tập Kết Hợp Với Hình Học Phẳng

Đề bài: Cho hình vuông ABCD nội tiếp trong đường tròn tâm O, bán kính R. Tính diện tích hình vuông ABCD theo R.

Hướng dẫn giải:

• Đường chéo của hình vuông bằng đường kính của đường tròn: AC = 2R
• Áp dụng định lý Pythagoras cho tam giác vuông ABC: AB² + BC² = AC²
• Vì AB = BC (hình vuông): 2AB² = (2R)² = 4R²
• Suy ra: AB² = 2R²
• Diện tích hình vuông ABCD: S = AB² = 2R²

5.2 Bài Tập Liên Quan Đến Tính Chất Tiếp Tuyến

Đề bài: Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn. Vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Chứng minh rằng OA vuông góc với BC tại trung điểm của BC.

Hướng dẫn giải:

• Tính chất hai tiếp tuyến cắt nhau: AB = AC và OB = OC = R
• Suy ra A thuộc đường trung trực của BC và O thuộc đường trung trực của BC
• Vậy OA là đường trung trực của BC, suy ra OA vuông góc với BC tại trung điểm của BC.

5.3 Bài Tập Ứng Dụng Trong Thực Tế

Đề bài: Một khu vườn hình tròn có bán kính 10m. Người ta muốn làm một con đường rộng 2m bao quanh khu vườn. Tính diện tích con đường đó.

Hướng dẫn giải:

• Bán kính khu vườn: r = 10m
• Bán kính khu vườn bao gồm cả con đường: R = r + 2 = 10 + 2 = 12m
• Diện tích khu vườn: S1 = πr² = π(10)² = 100π m²
• Diện tích khu vườn bao gồm cả con đường: S2 = πR² = π(12)² = 144π m²
• Diện tích con đường: S = S2 – S1 = 144π – 100π = 44π ≈ 138.23 m²

6. Mẹo Ghi Nhớ Kiến Thức Về Bán Kính và Đường Kính

6.1 Sử Dụng Hình Ảnh Trực Quan?

Sử dụng hình ảnh trực quan để minh họa khái niệm bán kính và đường kính giúp bạn dễ dàng hình dung và ghi nhớ kiến thức.

6.2 Liên Hệ Với Các Vật Dụng Hằng Ngày?

Liên hệ kiến thức về bán kính và đường kính với các vật dụng hàng ngày như bánh xe, đồng hồ, đĩa CD giúp bạn hiểu rõ hơn về ứng dụng của chúng trong thực tế.

6.3 Luyện Tập Thường Xuyên?

Luyện tập giải các bài tập về bán kính và đường kính thường xuyên giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.

6.4 Tạo Các Mối Liên Hệ?

Tạo các mối liên hệ giữa bán kính, đường kính, chu vi và diện tích hình tròn giúp bạn nắm vững kiến thức một cách hệ thống và logic.

7. Các Sai Lầm Thường Gặp Khi Học Về Bán Kính và Đường Kính

7.1 Nhầm Lẫn Giữa Bán Kính và Đường Kính?

Một sai lầm phổ biến là nhầm lẫn giữa bán kính và đường kính. Hãy nhớ rằng đường kính luôn gấp đôi bán kính.

7.2 Sai Sót Trong Tính Toán Chu Vi và Diện Tích?

Sai sót trong việc áp dụng công thức tính chu vi và diện tích hình tròn cũng là một lỗi thường gặp. Hãy kiểm tra kỹ công thức và các đơn vị đo trước khi thực hiện tính toán.

7.3 Không Hiểu Rõ Bản Chất Của Số Pi (π)?

Không hiểu rõ bản chất của số Pi (π) có thể dẫn đến sai sót trong tính toán. Hãy nhớ rằng π là một hằng số xấp xỉ 3.14159 và được sử dụng để tính chu vi và diện tích hình tròn.

8. Nguồn Tài Liệu Tham Khảo Về Hình Tròn, Bán Kính và Đường Kính Tại Tic.Edu.Vn

8.1 Các Bài Giảng Chi Tiết Về Hình Tròn?

tic.edu.vn cung cấp các bài giảng chi tiết về hình tròn, bao gồm định nghĩa, tính chất, công thức và các bài tập vận dụng.

8.2 Các Dạng Bài Tập Về Bán Kính và Đường Kính?

Bạn có thể tìm thấy nhiều dạng bài tập về bán kính và đường kính trên tic.edu.vn, từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng giải toán.

8.3 Các Ứng Dụng Thực Tế Của Hình Tròn?

tic.edu.vn cũng giới thiệu các ứng dụng thực tế của hình tròn trong đời sống, kỹ thuật, kiến trúc và các lĩnh vực khác, giúp bạn hiểu rõ hơn về tầm quan trọng của hình học.

8.4 Cộng Đồng Học Tập và Chia Sẻ Kiến Thức?

Tham gia cộng đồng học tập trên tic.edu.vn để trao đổi kiến thức, chia sẻ kinh nghiệm và giải đáp thắc mắc về hình tròn, bán kính và đường kính.

9. Các Công Cụ Hỗ Trợ Học Tập Về Hình Tròn, Bán Kính và Đường Kính

9.1 Phần Mềm Vẽ Hình Tròn Trực Tuyến?

Sử dụng các phần mềm vẽ hình tròn trực tuyến để tạo và khám phá các hình tròn với các kích thước khác nhau.

9.2 Máy Tính Chu Vi và Diện Tích Hình Tròn?

Sử dụng máy tính chu vi và diện tích hình tròn trực tuyến để kiểm tra kết quả tính toán và tiết kiệm thời gian.

9.3 Ứng Dụng Học Toán Hình Học?

Tải xuống các ứng dụng học toán hình học trên điện thoại hoặc máy tính bảng để học mọi lúc mọi nơi.

9.4 Công Cụ Tạo Bài Tập Trắc Nghiệm Về Hình Tròn?

Sử dụng các công cụ tạo bài tập trắc nghiệm về hình tròn để kiểm tra kiến thức và đánh giá khả năng của bản thân.

10. Lời Khuyên Để Học Tốt Về Bán Kính và Đường Kính

10.1 Nắm Vững Lý Thuyết Cơ Bản?

Hãy bắt đầu bằng việc nắm vững lý thuyết cơ bản về hình tròn, bán kính, đường kính, chu vi và diện tích.

10.2 Luyện Tập Giải Bài Tập Từ Dễ Đến Khó?

Luyện tập giải bài tập từ dễ đến khó giúp bạn làm quen với các dạng bài tập khác nhau và nâng cao kỹ năng giải toán.

10.3 Tìm Hiểu Các Ứng Dụng Thực Tế?

Tìm hiểu các ứng dụng thực tế của hình tròn trong đời sống và kỹ thuật giúp bạn thấy được tầm quan trọng của kiến thức và tạo động lực học tập.

10.4 Tham Gia Các Hoạt Động Học Tập Nhóm?

Tham gia các hoạt động học tập nhóm, trao đổi kiến thức với bạn bè và thầy cô giúp bạn hiểu sâu hơn về bán kính và đường kính.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin từ nhiều nguồn, và mong muốn có các công cụ hỗ trợ học tập hiệu quả? Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết những vấn đề này.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cập nhật thông tin giáo dục mới nhất và chính xác, sử dụng các công cụ hỗ trợ học tập trực tuyến hiệu quả, và tham gia cộng đồng học tập trực tuyến sôi nổi để trao đổi kiến thức và kinh nghiệm. Liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để được tư vấn và hỗ trợ tốt nhất. tic.edu.vn – Nơi chắp cánh ước mơ tri thức của bạn.

Câu hỏi thường gặp (FAQ) về Bán kính và Đường kính

Câu hỏi 1: Bán kính và đường kính có phải là hai khái niệm giống nhau không?

Không, bán kính và đường kính là hai khái niệm khác nhau. Bán kính là khoảng cách từ tâm của hình tròn đến một điểm bất kỳ trên đường tròn, trong khi đường kính là khoảng cách giữa hai điểm trên đường tròn đi qua tâm. Đường kính luôn gấp đôi bán kính.

Câu hỏi 2: Làm thế nào để tính bán kính khi biết đường kính?

Để tính bán kính khi biết đường kính, bạn chia đường kính cho 2. Công thức là: r = d/2, trong đó r là bán kính và d là đường kính.

Câu hỏi 3: Làm thế nào để tính đường kính khi biết bán kính?

Để tính đường kính khi biết bán kính, bạn nhân bán kính với 2. Công thức là: d = 2r, trong đó d là đường kính và r là bán kính.

Câu hỏi 4: Bán kính và đường kính được sử dụng để làm gì?

Bán kính và đường kính được sử dụng để tính chu vi và diện tích của hình tròn, cũng như trong nhiều ứng dụng kỹ thuật, kiến trúc và thiết kế khác. Chúng là những yếu tố cơ bản để xác định kích thước và tính chất của hình tròn.

Câu hỏi 5: Tại sao cần phải học về bán kính và đường kính?

Học về bán kính và đường kính giúp bạn hiểu rõ hơn về hình học và các ứng dụng của nó trong thực tế. Kiến thức này cần thiết cho việc giải quyết các bài toán liên quan đến hình tròn, cũng như trong nhiều lĩnh vực khoa học và kỹ thuật.

Câu hỏi 6: Có những công cụ nào giúp học về bán kính và đường kính?

Có nhiều công cụ hỗ trợ học tập về bán kính và đường kính, bao gồm phần mềm vẽ hình tròn trực tuyến, máy tính chu vi và diện tích hình tròn, ứng dụng học toán hình học và các công cụ tạo bài tập trắc nghiệm.

Câu hỏi 7: Tôi có thể tìm thêm tài liệu về bán kính và đường kính ở đâu?

Bạn có thể tìm thêm tài liệu về bán kính và đường kính trên tic.edu.vn, bao gồm các bài giảng chi tiết, các dạng bài tập và các ứng dụng thực tế của hình tròn.

Câu hỏi 8: Làm thế nào để ghi nhớ kiến thức về bán kính và đường kính một cách hiệu quả?

Để ghi nhớ kiến thức về bán kính và đường kính một cách hiệu quả, bạn nên sử dụng hình ảnh trực quan, liên hệ với các vật dụng hàng ngày, luyện tập thường xuyên và tạo các mối liên hệ giữa các khái niệm.

Câu hỏi 9: Những sai lầm nào thường gặp khi học về bán kính và đường kính?

Những sai lầm thường gặp khi học về bán kính và đường kính bao gồm nhầm lẫn giữa bán kính và đường kính, sai sót trong tính toán chu vi và diện tích, và không hiểu rõ bản chất của số Pi (π).

Câu hỏi 10: Làm thế nào để giải quyết các bài tập khó về bán kính và đường kính?

Để giải quyết các bài tập khó về bán kính và đường kính, bạn nên nắm vững lý thuyết cơ bản, luyện tập giải bài tập từ dễ đến khó, tìm hiểu các ứng dụng thực tế và tham gia các hoạt động học tập nhóm.