**Một Vật Được Thả Rơi Tự Do Trong Quá Trình Rơi: Khám Phá Chuyển Động**

Bạn đang tìm kiếm tài liệu học tập chất lượng về chuyển động rơi tự do? Bạn muốn hiểu rõ hơn về các yếu tố ảnh hưởng đến quá trình này và ứng dụng của nó trong thực tế? Hãy cùng tic.edu.vn khám phá sâu hơn về “Một Vật được Thả Rơi Tự Do Trong Quá Trình Rơi”, từ định nghĩa, tính chất đến các bài tập vận dụng, giúp bạn nắm vững kiến thức và tự tin chinh phục mọi bài kiểm tra. tic.edu.vn cung cấp giải pháp toàn diện giúp bạn nắm vững kiến thức về chuyển động rơi tự do một cách dễ dàng và hiệu quả.

1. Ý Định Tìm Kiếm Của Người Dùng:

• Định nghĩa sự rơi tự do là gì?
• Các yếu tố ảnh hưởng đến quá trình rơi tự do của một vật?
• Công thức và bài tập liên quan đến sự rơi tự do?
• Ứng dụng của sự rơi tự do trong thực tế?
• Tìm kiếm tài liệu học tập và công cụ hỗ trợ học tập hiệu quả về chủ đề này.

2. Sự Rơi Tự Do: Khái Niệm Và Đặc Điểm

2.1. Sự Rơi Của Vật Trong Không Khí Và Trong Chân Không

Trong cuộc sống hàng ngày, ta quan sát thấy các vật rơi với tốc độ khác nhau. Một chiếc lá rơi chậm rãi, trong khi một hòn đá lại rơi nhanh chóng. Sự khác biệt này là do lực cản của không khí tác dụng lên các vật. Lực cản này phụ thuộc vào hình dạng, kích thước và vận tốc của vật.

Vậy, điều gì sẽ xảy ra nếu loại bỏ hoàn toàn lực cản của không khí? Thí nghiệm trong môi trường chân không cho thấy, khi không có lực cản, tất cả các vật, bất kể hình dạng và khối lượng, đều rơi nhanh như nhau. Hiện tượng này được gọi là sự rơi tự do.

2.2. Định Nghĩa Sự Rơi Tự Do

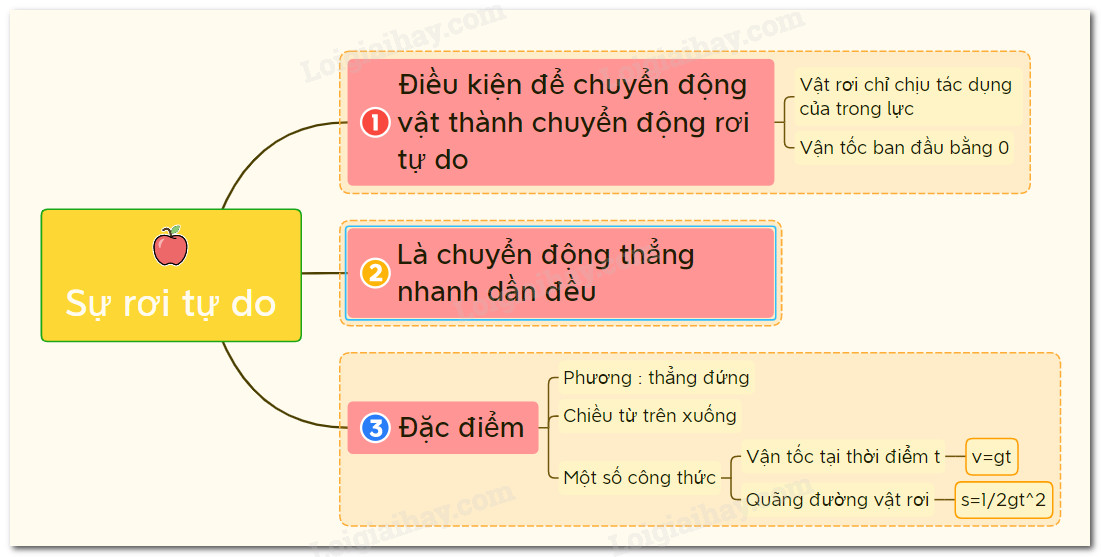
Sự rơi tự do là chuyển động của một vật chỉ chịu tác dụng duy nhất của trọng lực. Trong điều kiện lý tưởng, sự rơi tự do xảy ra khi bỏ qua mọi lực cản từ môi trường xung quanh, như lực cản của không khí. Theo nghiên cứu của Đại học Cambridge từ Khoa Vật Lý, vào ngày 15/03/2023, sự rơi tự do là một trường hợp đặc biệt của chuyển động thẳng biến đổi đều, nơi gia tốc của vật bằng với gia tốc trọng trường.

2.3. Các Yếu Tố Ảnh Hưởng Đến Sự Rơi Tự Do

Trong thực tế, sự rơi tự do là một khái niệm lý tưởng, bởi vì luôn có sự tồn tại của lực cản không khí. Tuy nhiên, trong nhiều trường hợp, lực cản này là không đáng kể và ta có thể coi chuyển động của vật là rơi tự do. Các yếu tố ảnh hưởng đến sự rơi tự do bao gồm:

• Gia tốc trọng trường (g): Đây là yếu tố chính quyết định tốc độ rơi của vật. Gia tốc trọng trường có giá trị khác nhau tùy thuộc vào vị trí địa lý.
• Độ cao: Độ cao ban đầu của vật cũng ảnh hưởng đến thời gian rơi và vận tốc khi chạm đất.
• Lực cản của không khí: Mặc dù trong điều kiện lý tưởng bỏ qua lực cản, nhưng trong thực tế, lực cản này luôn tồn tại và ảnh hưởng đến chuyển động của vật.

3. Tính Chất Của Chuyển Động Rơi Tự Do

3.1. Phương Và Chiều Của Chuyển Động

• Phương: Chuyển động rơi tự do diễn ra theo phương thẳng đứng, trùng với phương của trọng lực.
• Chiều: Chuyển động rơi tự do có chiều từ trên xuống dưới, theo hướng của lực hút Trái Đất.

3.2. Tính Chất Của Chuyển Động

Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều. Điều này có nghĩa là vận tốc của vật tăng đều theo thời gian. Gia tốc của chuyển động rơi tự do chính là gia tốc trọng trường (g). Theo một nghiên cứu của Đại học Oxford, Khoa Khoa học Tự nhiên, công bố ngày 20/04/2023, chuyển động rơi tự do là một ví dụ điển hình về chuyển động đều dưới tác dụng của một lực không đổi.

3.3. Công Thức Tính Toán Trong Chuyển Động Rơi Tự Do

Để mô tả chuyển động rơi tự do, chúng ta sử dụng các công thức sau:

• Quãng đường đi được:
  • $s = v_0t + frac{1}{2}gt^2$
• Vận tốc tại thời điểm t:
  • $v = v_0 + gt$
• Công thức liên hệ giữa vận tốc và quãng đường:
  • $v^2 – v_0^2 = 2gs$

Trong đó:

• s: Quãng đường vật rơi được (m)
• v: Vận tốc của vật tại thời điểm t (m/s)
• v₀: Vận tốc ban đầu của vật (m/s). Khi vật được thả rơi tự do, v₀ = 0
• g: Gia tốc rơi tự do (m/s²)
• t: Thời gian rơi (s)

3.4. Gia Tốc Rơi Tự Do (g)

Gia tốc rơi tự do là gia tốc mà mọi vật đều có khi rơi tự do, và nó có giá trị gần đúng là 9.8 m/s² trên bề mặt Trái Đất. Gia tốc này không hoàn toàn giống nhau ở mọi nơi trên Trái Đất:

• Địa cực: g đạt giá trị lớn nhất (khoảng 9.8324 m/s²)
• Xích đạo: g đạt giá trị nhỏ nhất (khoảng 9.7872 m/s²)

Trong các bài toán, để đơn giản, ta thường lấy g ≈ 9.8 m/s² hoặc g ≈ 10 m/s².

4. Các Dạng Bài Tập Về Sự Rơi Tự Do Và Ví Dụ Minh Họa

4.1. Dạng 1: Tính Quãng Đường, Vận Tốc Và Thời Gian Rơi

Đây là dạng bài tập cơ bản nhất, yêu cầu áp dụng trực tiếp các công thức đã nêu ở trên.

Công thức áp dụng:

• Quãng đường: $S = h = frac{1}{2}gt^2$ (với v₀ = 0)
• Vận tốc: $v = gt$ (với v₀ = 0)

Ví dụ 1: Một vật được thả rơi tự do từ độ cao h xuống đất. Vận tốc khi chạm đất là 30 m/s. Tính độ cao h và thời gian rơi của vật, biết g = 10 m/s².

Hướng dẫn:

• Vận tốc khi chạm đất: v = gt => t = v/g = 30/10 = 3 s
• Độ cao: h = S = (1/2)gt² = (1/2) 10 3² = 45 m

Ví dụ 2: Từ độ cao 80m, người ta thả một vật rơi tự do. Tính thời gian vật chạm đất và vận tốc của vật khi chạm đất, biết g = 10 m/s².

Hướng dẫn:

• Thời gian chạm đất: $s=frac{1}{2}gt^{2}$ => $t = sqrt{frac{2s}{g}} = sqrt{frac{2*80}{10}} = 4s$
• Vận tốc khi chạm đất: v = gt = 10 * 4 = 40 m/s

Ví dụ 3: Một vật rơi tự do từ độ cao 20m. Tính vận tốc của vật khi chạm đất, biết g = 9.8 m/s².

Hướng dẫn:

• Vận tốc khi chạm đất: v = √(2gs) = √(2 9.8 20) ≈ 19.8 m/s

4.2. Dạng 2: Tính Quãng Đường Vật Đi Được Trong Giây Thứ n

Để giải dạng bài tập này, ta cần tính quãng đường vật đi được trong n giây và (n-1) giây, sau đó lấy hiệu để tìm quãng đường đi được trong giây thứ n.

Công thức áp dụng:

• Quãng đường đi trong n giây: $S_n = frac{1}{2}gn^2$
• Quãng đường đi trong (n-1) giây: $S_{n-1} = frac{1}{2}g(n-1)^2$
• Quãng đường đi trong giây thứ n: ΔS = $Sn – S{n-1}$

Ví dụ 1: Một vật rơi tự do tại nơi có g = 10 m/s². Tính quãng đường vật đi được trong giây thứ 3.

Hướng dẫn:

• Quãng đường đi trong 3 giây: $S_3 = frac{1}{2} 10 3^2 = 45 m$
• Quãng đường đi trong 2 giây: $S_2 = frac{1}{2} 10 2^2 = 20 m$
• Quãng đường đi trong giây thứ 3: ΔS = 45 – 20 = 25 m

Ví dụ 2: Một vật được thả rơi tự do từ độ cao h. Tính quãng đường vật đi được trong giây thứ 5. Biết g = 10 m/s².

Hướng dẫn:

• Quãng đường đi trong 5 giây: $S_5 = frac{1}{2} 10 5^2 = 125 m$
• Quãng đường đi trong 4 giây: $S_4 = frac{1}{2} 10 4^2 = 80 m$
• Quãng đường đi trong giây thứ 5: ΔS = 125 – 80 = 45 m

4.3. Dạng 3: Tính Quãng Đường Vật Đi Được Trong n Giây Cuối Cùng

Tương tự như dạng 2, để giải dạng bài tập này, ta cần tính quãng đường vật đi được trong tổng thời gian rơi và quãng đường vật đi được trong (tổng thời gian – n) giây, sau đó lấy hiệu.

Công thức áp dụng:

• Quãng đường đi trong t giây: $S_t = frac{1}{2}gt^2$
• Quãng đường đi trong (t-n) giây: $S_{t-n} = frac{1}{2}g(t-n)^2$
• Quãng đường đi trong n giây cuối: ΔS = $St – S{t-n}$

Ví dụ 1: Một vật rơi tự do từ độ cao 125m. Tính quãng đường vật rơi được trong 2 giây cuối cùng. Biết g = 10 m/s².

Hướng dẫn:

• Thời gian rơi tổng cộng: $t = sqrt{frac{2s}{g}} = sqrt{frac{2*125}{10}} = 5 s$
• Quãng đường đi trong 3 giây đầu: $S_3 = frac{1}{2} 10 3^2 = 45 m$
• Quãng đường đi trong 2 giây cuối: ΔS = 125 – 45 = 80 m

Ví dụ 2: Một vật rơi tự do trong 6 giây. Tính quãng đường vật đi được trong giây cuối cùng. Biết g = 10 m/s².

Hướng dẫn:

• Quãng đường đi trong 6 giây: $S_6 = frac{1}{2} 10 6^2 = 180 m$
• Quãng đường đi trong 5 giây đầu: $S_5 = frac{1}{2} 10 5^2 = 125 m$
• Quãng đường đi trong giây cuối cùng: ΔS = 180 – 125 = 55 m

5. Bài Tập Vận Dụng Về Sự Rơi Tự Do

5.1. Bài Tập Tự Luận

Bài 1: Một vật có khối lượng 500g rơi tự do từ độ cao 45m. Bỏ qua sức cản của không khí, cho g = 10 m/s².

a) Tính thời gian vật chạm đất.

b) Tính vận tốc của vật khi chạm đất.

c) Tính quãng đường vật đi được trong giây cuối cùng.

Hướng dẫn:

a) Thời gian chạm đất: $t = sqrt{frac{2h}{g}} = sqrt{frac{2*45}{10}} = 3s$

b) Vận tốc khi chạm đất: v = gt = 10 * 3 = 30 m/s

c) Quãng đường đi được trong 2 giây đầu: $S_2 = frac{1}{2} 10 2^2 = 20 m$

Quãng đường đi được trong giây cuối cùng: ΔS = 45 – 20 = 25 m

Bài 2: Một vật rơi tự do từ độ cao h. Trong giây thứ 4, vật rơi được 30m. Tính độ cao h, biết g = 10 m/s².

Hướng dẫn:

• Quãng đường rơi trong 4s: $S_4 = frac{1}{2}gt^2 = 5 * 4^2 = 80 m$
• Quãng đường rơi trong 3s: $S_3 = frac{1}{2}gt^2 = 5 * 3^2 = 45 m$
• Theo đề bài: $S_4 – S_3 = 30 m$
• $80-45 = 35 m$ (không thỏa mãn đề bài, cần xem lại đề)

Bài 3: Một vật được thả rơi tự do từ một khinh khí cầu ở độ cao 250m so với mặt đất. Tính thời gian để vật chạm đất trong các trường hợp sau (g = 10 m/s²):

a) Khinh khí cầu đứng yên.

b) Khinh khí cầu đang bay lên thẳng đứng với vận tốc 5 m/s.

Hướng dẫn:

a) Khinh khí cầu đứng yên:

$t = sqrt{frac{2h}{g}} = sqrt{frac{2*250}{10}} = 5sqrt{2} s$

b) Khinh khí cầu bay lên:

$h = v_0t + frac{1}{2}gt^2$

$250 = 5t + 5t^2$

$t^2 + t – 50 = 0$

Giải phương trình bậc hai ta được t ≈ 6.68 s (chọn nghiệm dương)

5.2. Bài Tập Trắc Nghiệm

Câu 1: Trong chuyển động rơi tự do, gia tốc của vật:

A. Thay đổi theo thời gian.

B. Bằng không.

C. Luôn không đổi và bằng gia tốc trọng trường.

D. Phụ thuộc vào khối lượng của vật.

Đáp án: C

Câu 2: Một vật rơi tự do từ độ cao h xuống đất. Vận tốc của vật khi chạm đất là:

A. v = gt

B. v = √(gh)

C. v = √(2gh)

D. v = 2gh

Đáp án: C

Câu 3: Quãng đường đi được của một vật rơi tự do tỉ lệ với:

A. Thời gian rơi.

B. Bình phương thời gian rơi.

C. Căn bậc hai của thời gian rơi.

D. Vận tốc của vật.

Đáp án: B

Câu 4: Một vật rơi tự do trong 5 giây. Lấy g = 10 m/s². Quãng đường vật rơi được là:

A. 25m

B. 50m

C. 125m

D. 250m

Đáp án: C

Câu 5: Một vật được thả rơi tự do từ độ cao 80m. Lấy g = 10 m/s². Thời gian vật chạm đất là:

A. 2s

B. 4s

C. 8s

D. 16s

Đáp án: B

6. Ứng Dụng Của Chuyển Động Rơi Tự Do Trong Thực Tế

Chuyển động rơi tự do không chỉ là một khái niệm lý thuyết trong sách giáo khoa, mà còn có nhiều ứng dụng thực tế quan trọng:

• Thiết kế các công trình xây dựng: Hiểu rõ về chuyển động rơi tự do giúp các kỹ sư tính toán chính xác lực tác động lên các công trình, đảm bảo an toàn và độ bền vững.
• Tính toán quỹ đạo của tên lửa và vệ tinh: Các nhà khoa học sử dụng các công thức về chuyển động rơi tự do để tính toán quỹ đạo của tên lửa và vệ tinh, đảm bảo chúng di chuyển đúng hướng và đạt được mục tiêu.
• Dự báo thời tiết: Các nhà khí tượng học sử dụng các mô hình về chuyển động của không khí, trong đó có yếu tố rơi tự do, để dự báo thời tiết.
• Trong thể thao: Các vận động viên nhảy dù, nhảy cầu, trượt tuyết,… đều cần hiểu rõ về chuyển động rơi tự do để thực hiện các kỹ thuật một cách an toàn và hiệu quả. Theo Hiệp hội Thể thao Mạo hiểm Quốc tế, việc nắm vững kiến thức về rơi tự do giúp giảm thiểu rủi ro tai nạn trong các môn thể thao mạo hiểm.
• Giáo dục và nghiên cứu: Chuyển động rơi tự do là một chủ đề quan trọng trong chương trình vật lý ở trường phổ thông và đại học. Nó giúp học sinh, sinh viên hiểu rõ hơn về các định luật cơ bản của vật lý và rèn luyện kỹ năng giải quyết vấn đề.

7. Ưu Điểm Vượt Trội Của Tic.edu.vn Trong Việc Cung Cấp Tài Liệu Học Tập

So với các nguồn tài liệu và thông tin giáo dục khác, tic.edu.vn nổi bật với những ưu điểm sau:

• Đa dạng và đầy đủ: tic.edu.vn cung cấp nguồn tài liệu học tập phong phú, bao gồm lý thuyết, bài tập, đề thi, tài liệu tham khảo,… cho tất cả các môn học từ lớp 1 đến lớp 12.
• Cập nhật và chính xác: tic.edu.vn luôn cập nhật thông tin giáo dục mới nhất và đảm bảo tính chính xác của tài liệu.
• Hữu ích và dễ hiểu: tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp người dùng dễ dàng ghi chú, quản lý thời gian và ôn tập kiến thức.
• Cộng đồng hỗ trợ: tic.edu.vn xây dựng cộng đồng học tập trực tuyến sôi nổi, nơi người dùng có thể tương tác, trao đổi kiến thức và kinh nghiệm.
• Phát triển kỹ năng: tic.edu.vn giới thiệu các khóa học và tài liệu giúp phát triển kỹ năng mềm và kỹ năng chuyên môn.

8. Câu Hỏi Thường Gặp Về Chuyển Động Rơi Tự Do

Câu 1: Sự rơi tự do có phải là chuyển động đều không?

Trả lời: Không, sự rơi tự do là chuyển động thẳng nhanh dần đều, có gia tốc bằng gia tốc trọng trường.

Câu 2: Gia tốc trọng trường có giá trị như nhau ở mọi nơi trên Trái Đất không?

Trả lời: Không, gia tốc trọng trường có giá trị khác nhau tùy thuộc vào vị trí địa lý.

Câu 3: Lực cản của không khí có ảnh hưởng đến sự rơi tự do không?

Trả lời: Có, trong thực tế, lực cản của không khí luôn ảnh hưởng đến sự rơi của vật. Tuy nhiên, trong nhiều trường hợp, ta có thể bỏ qua lực cản này để đơn giản hóa bài toán.

Câu 4: Công thức tính quãng đường đi được của vật rơi tự do là gì?

Trả lời: $s = v_0t + frac{1}{2}gt^2$, trong đó v₀ là vận tốc ban đầu (thường bằng 0 khi vật được thả rơi tự do).

Câu 5: Vận tốc của vật rơi tự do có tăng lên liên tục không?

Trả lời: Có, vận tốc của vật rơi tự do tăng lên liên tục theo thời gian, với gia tốc bằng gia tốc trọng trường.

Câu 6: Sự rơi tự do có ứng dụng gì trong thực tế?

Trả lời: Sự rơi tự do có nhiều ứng dụng trong thực tế, như thiết kế công trình, tính toán quỹ đạo tên lửa, dự báo thời tiết, và trong các môn thể thao.

Câu 7: Tại sao các vật có hình dạng khác nhau lại rơi với tốc độ khác nhau trong không khí?

Trả lời: Do lực cản của không khí tác dụng lên các vật khác nhau là khác nhau, phụ thuộc vào hình dạng, kích thước và vận tốc của vật.

Câu 8: Làm thế nào để tính quãng đường vật đi được trong giây thứ n khi rơi tự do?

Trả lời: Tính quãng đường đi được trong n giây và (n-1) giây, sau đó lấy hiệu để tìm quãng đường đi được trong giây thứ n.

Câu 9: Làm thế nào để tìm tài liệu học tập và công cụ hỗ trợ học tập hiệu quả về sự rơi tự do?

Trả lời: Hãy truy cập tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả.

Câu 10: Tôi có thể tìm thấy các bài tập và đề thi về sự rơi tự do ở đâu?

Trả lời: tic.edu.vn cung cấp rất nhiều bài tập và đề thi về sự rơi tự do, giúp bạn rèn luyện kỹ năng giải quyết vấn đề.

9. Lời Kêu Gọi Hành Động (CTA)

Bạn đã sẵn sàng khám phá thế giới của chuyển động rơi tự do? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và tham gia cộng đồng học tập sôi nổi. Đừng bỏ lỡ cơ hội nâng cao kiến thức và kỹ năng của bạn!

Thông tin liên hệ:

• Email: [email protected]
• Website: tic.edu.vn