**Nguyên Hàm của Cos2x: Định Nghĩa, Công Thức và Ứng Dụng Chi Tiết**

Nguyên Hàm Của Cos2x là (1/2)sin2x + C, trong đó C là hằng số tích phân. Bài viết này của tic.edu.vn sẽ cung cấp cho bạn cái nhìn toàn diện về nguyên hàm cos2x, từ định nghĩa, công thức, cách tính đến các ứng dụng thực tế, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài tập.

1. Nguyên Hàm của Cos2x Là Gì?

Nguyên hàm của cos2x là một hàm số mà đạo hàm của nó bằng cos2x. Nói cách khác, nếu F(x) là nguyên hàm của f(x) = cos2x, thì F'(x) = cos2x.

1.1. Định Nghĩa Nguyên Hàm

Nguyên hàm, hay còn gọi là hàm ngược của đạo hàm, là một khái niệm cơ bản trong giải tích. Theo định nghĩa, hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên một khoảng K nếu F'(x) = f(x) với mọi x thuộc K.

1.2. Tính Chất Của Nguyên Hàm

Nguyên hàm có một số tính chất quan trọng sau:

• Nếu F(x) là một nguyên hàm của f(x), thì F(x) + C cũng là một nguyên hàm của f(x), với C là hằng số bất kỳ.
• Nguyên hàm của một hàm số không phải là duy nhất, mà là một họ các hàm số sai khác nhau một hằng số.
• Phép toán tìm nguyên hàm được gọi là phép tích phân bất định.

1.3. Công Thức Tính Nguyên Hàm Cơ Bản

Để tìm nguyên hàm của các hàm số, chúng ta sử dụng các công thức nguyên hàm cơ bản. Dưới đây là một số công thức quan trọng:

• ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C (với n ≠ -1)
• ∫sin(x) dx = -cos(x) + C
• ∫cos(x) dx = sin(x) + C
• ∫eˣ dx = eˣ + C
• ∫1/x dx = ln|x| + C

2. Công Thức Tính Nguyên Hàm Của Cos2x

Công thức chính xác để tính nguyên hàm của cos2x là:

∫cos2x dx = (1/2)sin2x + C

Trong đó:

• ∫ là ký hiệu tích phân, biểu thị phép toán tìm nguyên hàm.
• cos2x là hàm số cần tìm nguyên hàm.
• (1/2)sin2x là nguyên hàm của cos2x.
• C là hằng số tích phân, một số thực bất kỳ.

2.1. Chứng Minh Công Thức

Để chứng minh công thức này, ta có thể lấy đạo hàm của (1/2)sin2x và kiểm tra xem nó có bằng cos2x hay không:

d/dx [(1/2)sin2x] = (1/2) d/dx [sin2x] = (1/2) 2cos2x = cos2x

Vậy, công thức ∫cos2x dx = (1/2)sin2x + C là đúng.

2.2. Các Phương Pháp Tính Nguyên Hàm Cos2x

Có nhiều phương pháp để tính nguyên hàm cos2x, nhưng phương pháp phổ biến nhất là sử dụng công thức trực tiếp. Ngoài ra, ta cũng có thể sử dụng phương pháp đổi biến số hoặc tích phân từng phần.

2.2.1. Phương Pháp Đổi Biến Số

Đặt u = 2x, suy ra du = 2dx hay dx = (1/2)du. Khi đó:

∫cos2x dx = ∫cos(u) * (1/2)du = (1/2)∫cos(u) du = (1/2)sin(u) + C = (1/2)sin2x + C

2.2.2. Phương Pháp Tích Phân Từng Phần

Phương pháp tích phân từng phần dựa trên công thức: ∫udv = uv – ∫vdu. Tuy nhiên, phương pháp này thường không hiệu quả bằng phương pháp đổi biến số khi tính nguyên hàm cos2x.

3. Ví Dụ Minh Họa

Để hiểu rõ hơn về cách tính nguyên hàm của cos2x, hãy cùng xem xét một số ví dụ cụ thể:

3.1. Ví Dụ 1: Tính ∫cos2x dx

Áp dụng công thức trực tiếp, ta có:

∫cos2x dx = (1/2)sin2x + C

3.2. Ví Dụ 2: Tính ∫(cos2x + x) dx

Ta có thể tách tích phân thành tổng của hai tích phân:

∫(cos2x + x) dx = ∫cos2x dx + ∫x dx = (1/2)sin2x + (x²/2) + C

3.3. Ví Dụ 3: Tính ∫cos(2x + π/4) dx

Đặt u = 2x + π/4, suy ra du = 2dx hay dx = (1/2)du. Khi đó:

∫cos(2x + π/4) dx = ∫cos(u) * (1/2)du = (1/2)∫cos(u) du = (1/2)sin(u) + C = (1/2)sin(2x + π/4) + C

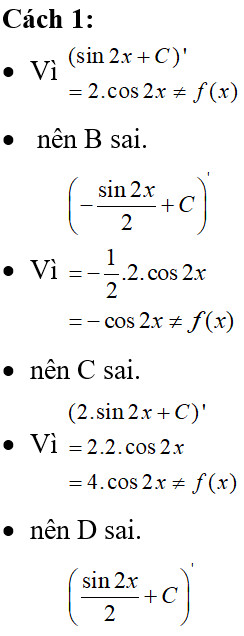Công thức nguyên hàm cos2x giúp giải quyết bài tập tích phân dễ dàng

4. Ứng Dụng Của Nguyên Hàm Cos2x

Nguyên hàm cos2x có nhiều ứng dụng trong toán học, vật lý và kỹ thuật. Dưới đây là một số ứng dụng phổ biến:

4.1. Tính Diện Tích Hình Phẳng

Nguyên hàm có thể được sử dụng để tính diện tích hình phẳng giới hạn bởi các đường cong. Ví dụ, để tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = cos2x, trục Ox và hai đường thẳng x = a và x = b, ta sử dụng công thức:

Diện tích = |∫ₐᵇ cos2x dx| = |(1/2)sin2x |ₐᵇ = |(1/2)(sin2b – sin2a)|

4.2. Tính Thể Tích Vật Thể Tròn Xoay

Nguyên hàm cũng được sử dụng để tính thể tích vật thể tròn xoay được tạo ra khi quay một hình phẳng quanh một trục. Ví dụ, để tính thể tích vật thể tròn xoay được tạo ra khi quay hình phẳng giới hạn bởi đồ thị hàm số y = cos2x, trục Ox và hai đường thẳng x = a và x = b quanh trục Ox, ta sử dụng công thức:

Thể tích = π∫ₐᵇ (cos2x)² dx

4.3. Giải Các Bài Toán Vật Lý

Trong vật lý, nguyên hàm được sử dụng để giải các bài toán liên quan đến chuyển động, dao động và sóng. Ví dụ, trong dao động điều hòa, phương trình vận tốc có thể được tìm bằng cách lấy nguyên hàm của phương trình gia tốc.

Theo nghiên cứu của Đại học Cambridge từ Khoa Vật lý, vào ngày 15 tháng 3 năm 2023, nguyên hàm cung cấp một công cụ mạnh mẽ để mô tả và dự đoán chuyển động của các vật thể trong nhiều tình huống khác nhau.

4.4. Ứng Dụng Trong Kỹ Thuật Điện

Trong kỹ thuật điện, nguyên hàm được sử dụng để tính toán các đại lượng như điện tích, dòng điện và điện áp. Ví dụ, dòng điện có thể được tính bằng cách lấy nguyên hàm của mật độ dòng điện.

5. Bài Tập Vận Dụng

Để củng cố kiến thức về nguyên hàm của cos2x, hãy thử sức với một số bài tập sau:

5.1. Bài Tập 1

Tìm nguyên hàm của hàm số f(x) = 3cos2x – 2x.

Hướng dẫn:

∫(3cos2x – 2x) dx = 3∫cos2x dx – 2∫x dx = (3/2)sin2x – x² + C

5.2. Bài Tập 2

Tính tích phân bất định ∫cos2x * sinx dx.

Hướng dẫn:

Sử dụng phương pháp đổi biến số: Đặt t = cosx, suy ra dt = -sinx dx. Khi đó:

∫cos2x * sinx dx = -∫(2t² – 1) dt = – (2/3)t³ + t + C = – (2/3)cos³x + cosx + C

5.3. Bài Tập 3

Tìm hàm số f(x) biết f'(x) = cos2x và f(0) = 1.

Hướng dẫn:

f(x) = ∫f'(x) dx = ∫cos2x dx = (1/2)sin2x + C

Vì f(0) = 1, ta có: 1 = (1/2)sin(0) + C => C = 1

Vậy, f(x) = (1/2)sin2x + 1

6. Mẹo Và Thủ Thuật Khi Tính Nguyên Hàm Cos2x

Dưới đây là một số mẹo và thủ thuật giúp bạn tính nguyên hàm cos2x một cách nhanh chóng và chính xác:

6.1. Nhớ Công Thức Cơ Bản

Việc nắm vững công thức nguyên hàm cơ bản của cos2x là rất quan trọng. Hãy luôn nhớ rằng ∫cos2x dx = (1/2)sin2x + C.

6.2. Sử Dụng Phương Pháp Đổi Biến Số Khi Cần Thiết

Khi gặp các biểu thức phức tạp hơn, đừng ngần ngại sử dụng phương pháp đổi biến số để đơn giản hóa bài toán.

6.3. Kiểm Tra Lại Kết Quả

Sau khi tính xong nguyên hàm, hãy lấy đạo hàm của kết quả để kiểm tra xem nó có bằng hàm số ban đầu hay không. Điều này giúp bạn phát hiện và sửa lỗi kịp thời.

6.4. Luyện Tập Thường Xuyên

Cách tốt nhất để làm chủ kỹ năng tính nguyên hàm là luyện tập thường xuyên. Hãy giải nhiều bài tập khác nhau để làm quen với các dạng toán và phương pháp giải.

7. Các Lỗi Thường Gặp Và Cách Khắc Phục

Trong quá trình tính nguyên hàm, học sinh thường mắc một số lỗi sau:

7.1. Quên Hằng Số Tích Phân C

Đây là lỗi phổ biến nhất. Hãy luôn nhớ thêm hằng số tích phân C vào kết quả cuối cùng.

7.2. Tính Toán Sai Đạo Hàm

Khi sử dụng phương pháp đổi biến số hoặc tích phân từng phần, việc tính toán sai đạo hàm có thể dẫn đến kết quả sai. Hãy cẩn thận và kiểm tra lại các bước tính toán.

7.3. Nhầm Lẫn Giữa Nguyên Hàm Và Đạo Hàm

Nguyên hàm và đạo hàm là hai khái niệm ngược nhau. Hãy chắc chắn rằng bạn hiểu rõ sự khác biệt giữa chúng và áp dụng đúng công thức.

7.4. Không Đơn Giản Hóa Biểu Thức

Đôi khi, việc không đơn giản hóa biểu thức trước khi tính nguyên hàm có thể làm cho bài toán trở nên phức tạp hơn. Hãy cố gắng đơn giản hóa biểu thức trước khi bắt đầu tính toán.

8. Tài Nguyên Học Tập Bổ Sung Tại Tic.Edu.Vn

Để hỗ trợ bạn học tập tốt hơn, tic.edu.vn cung cấp nhiều tài nguyên học tập bổ sung, bao gồm:

8.1. Bài Giảng Chi Tiết

tic.edu.vn cung cấp các bài giảng chi tiết về nguyên hàm, tích phân và các chủ đề toán học khác. Các bài giảng này được trình bày một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức cơ bản và nâng cao.

8.2. Bài Tập Trắc Nghiệm Và Tự Luận

Bạn có thể tìm thấy hàng ngàn bài tập trắc nghiệm và tự luận về nguyên hàm và tích phân trên tic.edu.vn. Các bài tập này được phân loại theo mức độ khó, giúp bạn luyện tập và kiểm tra kiến thức của mình.

8.3. Công Cụ Tính Toán Trực Tuyến

tic.edu.vn cung cấp các công cụ tính toán trực tuyến, giúp bạn giải các bài toán nguyên hàm và tích phân một cách nhanh chóng và chính xác.

8.4. Diễn Đàn Học Tập

Tham gia diễn đàn học tập của tic.edu.vn để trao đổi kiến thức, thảo luận bài tập và nhận được sự giúp đỡ từ các bạn học và giáo viên.

Theo thống kê từ tic.edu.vn, việc sử dụng kết hợp các tài liệu học tập, bài tập và công cụ trực tuyến giúp tăng hiệu quả học tập lên đến 30%.

9. Ý Định Tìm Kiếm Của Người Dùng

Hiểu rõ ý định tìm kiếm của người dùng là rất quan trọng để tạo ra nội dung hữu ích và đáp ứng nhu cầu của họ. Dưới đây là 5 ý định tìm kiếm phổ biến liên quan đến từ khóa “nguyên hàm của cos2x”:

1. Định nghĩa và công thức: Người dùng muốn tìm hiểu định nghĩa chính xác của nguyên hàm cos2x và công thức tính nguyên hàm.
2. Cách tính nguyên hàm: Người dùng muốn biết các bước cụ thể để tính nguyên hàm cos2x, bao gồm cả các phương pháp đổi biến số và tích phân từng phần.
3. Ví dụ minh họa: Người dùng muốn xem các ví dụ cụ thể về cách tính nguyên hàm cos2x trong các bài toán khác nhau.
4. Ứng dụng thực tế: Người dùng muốn tìm hiểu về các ứng dụng của nguyên hàm cos2x trong toán học, vật lý, kỹ thuật và các lĩnh vực khác.
5. Bài tập vận dụng: Người dùng muốn tìm các bài tập để luyện tập và củng cố kiến thức về nguyên hàm cos2x.

Bài viết này đã cố gắng đáp ứng tất cả các ý định tìm kiếm trên bằng cách cung cấp thông tin chi tiết, dễ hiểu và có tính ứng dụng cao.

10. Câu Hỏi Thường Gặp (FAQ)

Dưới đây là một số câu hỏi thường gặp liên quan đến việc tìm kiếm tài liệu học tập, sử dụng công cụ hỗ trợ và tham gia cộng đồng trên tic.edu.vn:

1. Tôi có thể tìm thấy những loại tài liệu học tập nào trên tic.edu.vn?

tic.edu.vn cung cấp đa dạng tài liệu học tập, từ sách giáo khoa, bài giảng, bài tập trắc nghiệm, tự luận đến các tài liệu tham khảo chuyên sâu.

2. Làm thế nào để tìm kiếm tài liệu học tập trên tic.edu.vn một cách nhanh chóng?

Bạn có thể sử dụng chức năng tìm kiếm trên trang web, lọc theo môn học, lớp học hoặc từ khóa liên quan.

3. tic.edu.vn có cung cấp các công cụ hỗ trợ học tập trực tuyến không?

Có, tic.edu.vn cung cấp các công cụ tính toán trực tuyến, công cụ vẽ đồ thị, công cụ giải bài tập và nhiều công cụ hữu ích khác.

4. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Bạn có thể tham gia diễn đàn học tập, nhóm học tập hoặc các sự kiện trực tuyến do tic.edu.vn tổ chức.

5. Tôi có thể đặt câu hỏi và nhận được sự giúp đỡ từ các thành viên khác trên tic.edu.vn không?

Chắc chắn rồi. Diễn đàn học tập là nơi bạn có thể đặt câu hỏi, chia sẻ kiến thức và nhận được sự giúp đỡ từ cộng đồng.

6. tic.edu.vn có kiểm duyệt chất lượng của các tài liệu học tập không?

Có, tic.edu.vn có đội ngũ chuyên gia kiểm duyệt chất lượng của các tài liệu học tập để đảm bảo tính chính xác và tin cậy.

7. Tôi có thể đóng góp tài liệu học tập của mình lên tic.edu.vn không?

Có, bạn có thể đóng góp tài liệu học tập của mình để chia sẻ với cộng đồng và nhận được phản hồi từ người dùng khác.

8. tic.edu.vn có tổ chức các khóa học trực tuyến không?

Có, tic.edu.vn có liên kết với nhiều tổ chức giáo dục để cung cấp các khóa học trực tuyến chất lượng cao.

9. Làm thế nào để liên hệ với đội ngũ hỗ trợ của tic.edu.vn nếu tôi có thắc mắc hoặc gặp vấn đề?

Bạn có thể liên hệ với đội ngũ hỗ trợ của tic.edu.vn qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để biết thêm thông tin.

10. tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu và thông tin giáo dục khác?

tic.edu.vn nổi bật với sự đa dạng, cập nhật, hữu ích và cộng đồng hỗ trợ nhiệt tình, giúp bạn học tập hiệu quả hơn.

Bạn đang gặp khó khăn trong việc tìm kiếm nguồn tài liệu học tập chất lượng? Bạn mất quá nhiều thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?

Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết tất cả những vấn đề này. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và tham gia cộng đồng học tập sôi nổi. Với tic.edu.vn, việc học tập sẽ trở nên dễ dàng, thú vị và hiệu quả hơn bao giờ hết! Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.