







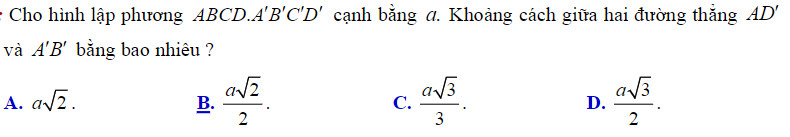





Khoảng Cách Giữa 2 đường Thẳng là một khái niệm quan trọng trong hình học không gian, đặc biệt trong chương trình toán học phổ thông. Bài viết này của tic.edu.vn sẽ cung cấp cho bạn cái nhìn toàn diện về khoảng cách giữa hai đường thẳng, từ định nghĩa, các phương pháp tính toán đến bài tập vận dụng, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán liên quan.
Contents
1. Hiểu Rõ Về Khoảng Cách Giữa Hai Đường Thẳng
Khoảng cách giữa hai đường thẳng là gì và nó quan trọng như thế nào trong hình học không gian?
1.1. Định Nghĩa Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau
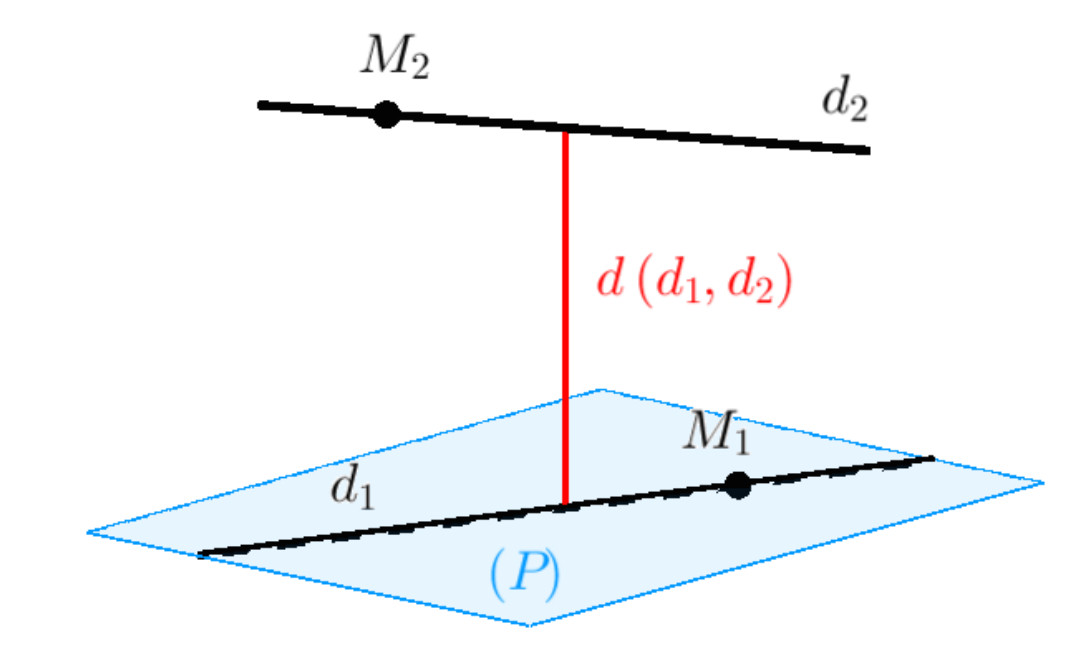
Trong không gian Oxyz, hai đường thẳng có thể có bốn vị trí tương đối: trùng nhau, cắt nhau, song song và chéo nhau. Khi hai đường thẳng ở vị trí chéo nhau, khoảng cách giữa chúng được định nghĩa là độ dài của đoạn vuông góc chung. Đoạn vuông góc chung này là đoạn thẳng nối hai điểm trên hai đường thẳng chéo nhau, đồng thời vuông góc với cả hai đường thẳng đó.
Đoạn vuông góc chung giữa hai đường thẳng chéo nhau là duy nhất.
1.2. Ý Nghĩa Của Việc Tính Khoảng Cách Giữa Hai Đường Thẳng
Việc tính khoảng cách giữa hai đường thẳng không chỉ là một bài toán hình học đơn thuần, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực như:
- Kiến trúc và xây dựng: Xác định khoảng cách an toàn giữa các cấu trúc, đảm bảo tính ổn định và an toàn của công trình.
- Thiết kế máy móc: Tính toán khoảng cách giữa các bộ phận chuyển động để tránh va chạm và đảm bảo hiệu suất hoạt động.
- Đồ họa máy tính và trò chơi điện tử: Mô phỏng chính xác khoảng cách giữa các đối tượng trong không gian ba chiều, tạo ra trải nghiệm chân thực cho người dùng.
- Robot học: Lập trình cho robot di chuyển và tương tác với môi trường xung quanh một cách chính xác và an toàn.
2. Các Phương Pháp Tính Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau
Để tính khoảng cách giữa hai đường thẳng chéo nhau, bạn cần nắm vững các phương pháp cơ bản như tính khoảng cách từ một điểm đến một mặt phẳng, cách dựng hình chiếu vuông góc trên mặt phẳng… Dưới đây là ba phương pháp thường được sử dụng để giải quyết các bài toán liên quan.
2.1. Phương Pháp 1: Dựng Đoạn Vuông Góc Chung Và Tính Độ Dài
Đây là phương pháp trực quan và thường được sử dụng nhất khi giải các bài tập về khoảng cách giữa hai đường thẳng chéo nhau. Công thức tổng quát được biểu diễn như sau:
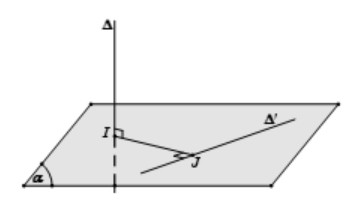
Khi hai đường thẳng a và b vừa chéo nhau, vừa vuông góc với nhau, thường tồn tại một mặt phẳng () chứa đường thẳng a và vuông góc với đường thẳng b. Để dựng đoạn vuông góc chung, ta thực hiện hai bước sau:
- Tìm giao điểm H: Xác định điểm H thuộc đường thẳng b và nằm trong mặt phẳng ().
- Dựng HK vuông góc với a: Trong mặt phẳng (), dựng đoạn HK vuông góc với đường thẳng a tại K. Khi đó, HK chính là đoạn vuông góc chung của đường thẳng a và đường thẳng b. Sau đó, áp dụng các công thức tính khoảng cách để tính toán.
Lưu ý: Phương pháp này đặc biệt hiệu quả khi hai đường thẳng a và b vuông góc với nhau. Trong trường hợp đó, việc tìm và dựng đường vuông góc chung trở nên đơn giản hơn nhiều. Tuy nhiên, nếu hai đường thẳng không vuông góc, việc dựng đường vuông góc chung có thể trở nên phức tạp.
Ví dụ minh họa:
2.2. Phương Pháp 2: Tính Khoảng Cách Từ Đường Thẳng Đến Mặt Phẳng Song Song
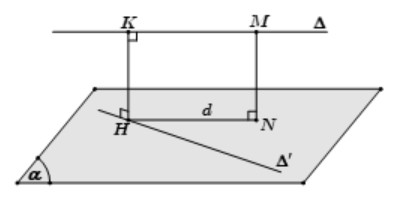
Khi hai đường thẳng a và b chéo nhau nhưng không vuông góc, ta có thể áp dụng phương pháp tính khoảng cách từ một đường thẳng đến một mặt phẳng song song với nó và chứa đường thẳng còn lại. Các bước thực hiện như sau:
- Chọn mặt phẳng (α): Chọn mặt phẳng (α) chứa đường thẳng b và song song với đường thẳng a.
- Dựng hình chiếu vuông góc d: Dựng đường thẳng d là hình chiếu vuông góc của đường thẳng a xuống mặt phẳng (α). Để làm điều này, lấy một điểm M bất kỳ trên đường thẳng a, dựng đoạn MN vuông góc với mặt phẳng (α). Khi đó, đường thẳng d sẽ đi qua N và song song với a.
- Xác định đoạn vuông góc chung HK: Gọi H là giao điểm của d và b, từ đó dựng HK song song với MN.
Như vậy, HK chính là đoạn vuông góc chung của hai đường thẳng a và b. Độ dài đoạn vuông góc chung này bằng độ dài đoạn MN.
Ví dụ minh họa:
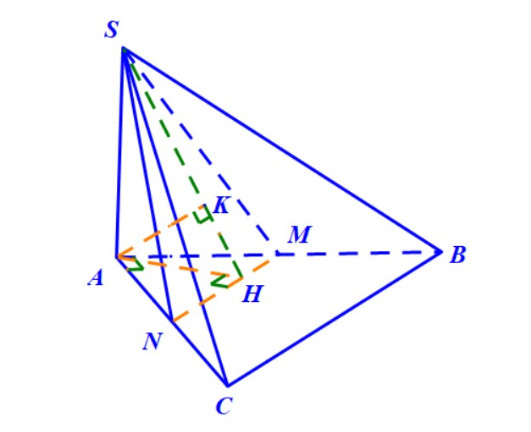
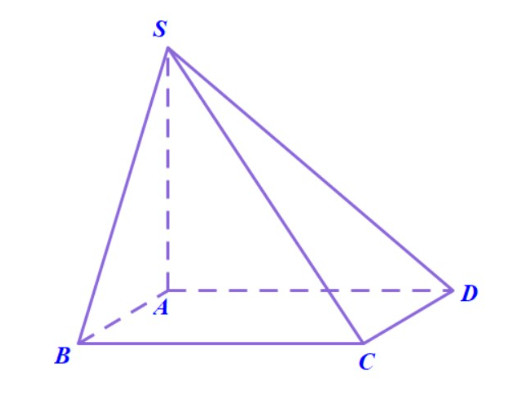
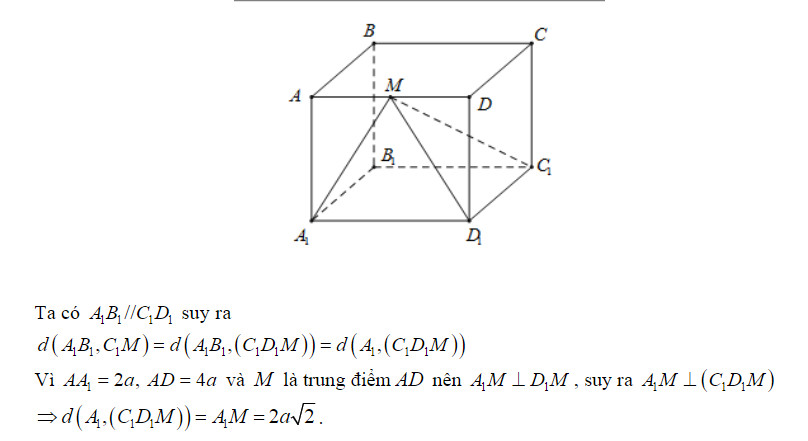
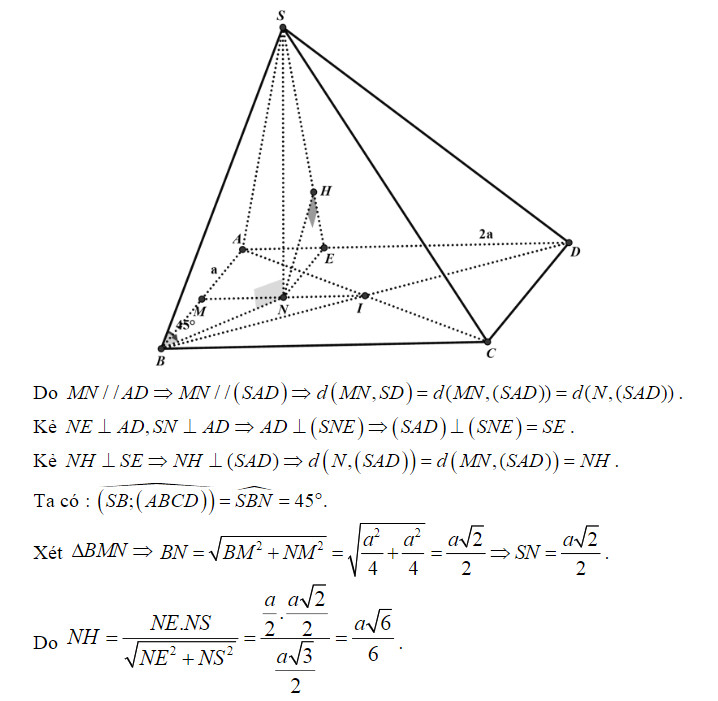
Ví dụ 1: (Trích câu 40 đề minh họa THPT Quốc gia 2020) Cho hình chóp S.ABCD có SA vuông góc với đáy (ABC), SA = a, tam giác ABC vuông tại A, AC = 4a, AB = 2a. Gọi M là trung điểm của AB. Tính khoảng cách giữa hai đường thẳng SM và BC.
Giải:
Gọi N là trung điểm của AC, ta có:
Suy ra:
Vì AB cắt mặt phẳng (SMN) tại trung điểm M, nên:
Lần lượt kẻ AH ⊥ MN và AK ⊥ SH, áp dụng kết quả hình chóp có 3 tia đồng quy và đôi một vuông góc với nhau, ta có:
Thay số vào ta được .
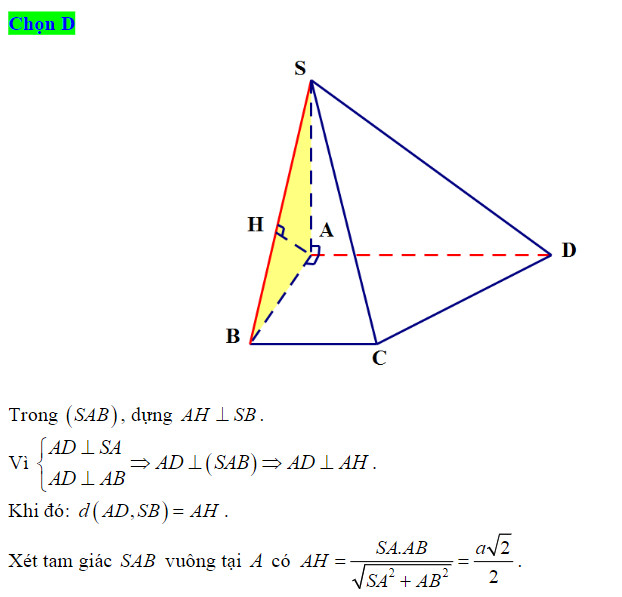
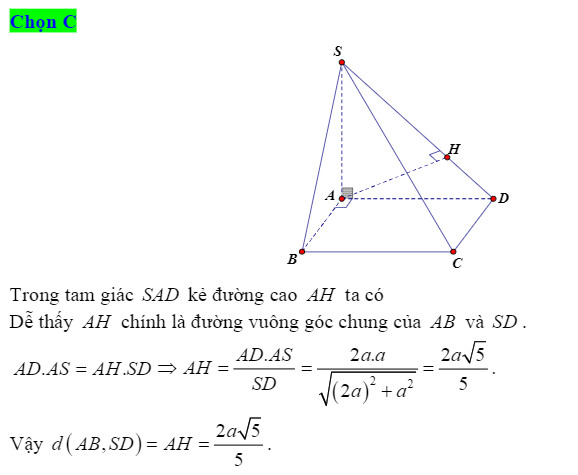
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = a và SA vuông góc với đáy. Tính khoảng cách giữa hai đoạn AB và SC.
Giải:
Ta có AB // CD ⇒ AB // (SCD). Do đó:
Kẻ đường cao AK thuộc tam giác SAD, ta có khoảng cách cần tìm là:
2.3. Phương Pháp 3: Tính Khoảng Cách Giữa Hai Mặt Phẳng Song Song
Phương pháp này chuyển việc tính khoảng cách giữa hai đường thẳng chéo nhau thành việc tính khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó. Công thức tổng quát như sau:
Lưu ý: Phương pháp này thường được sử dụng khi việc kẻ đường thẳng song song với một trong hai đường thẳng ban đầu gặp khó khăn.
Ví dụ minh họa:
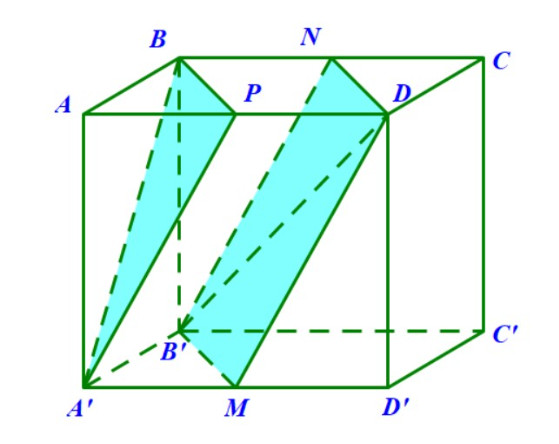
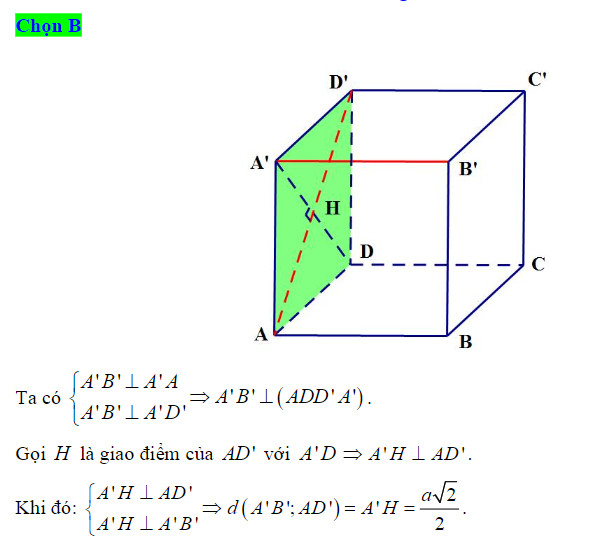
Ví dụ 1: (Đề Đại học khối B năm 2002) Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính khoảng cách giữa hai đường thẳng B’D và A’B theo a.
Giải:
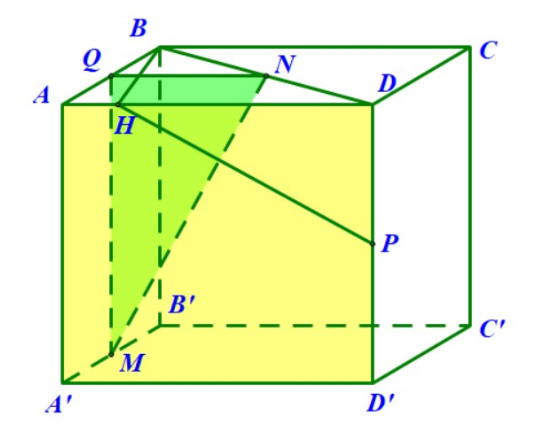
Ví dụ 2: Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình bình hành với AD = 2a, AB = a, góc BAD bằng 60 độ và . Gọi M, N, P lần lượt là trung điểm của A’B’, BD và DD’. Hình chiếu vuông góc của B lên AD là H. Tính khoảng cách giữa hai đường thẳng chéo nhau MN và HP.
Giải:
3. Bài Tập Vận Dụng Về Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau Oxyz
Để thành thạo việc tính khoảng cách giữa hai đường thẳng chéo nhau, hãy cùng tic.edu.vn giải các bài tập sau đây.
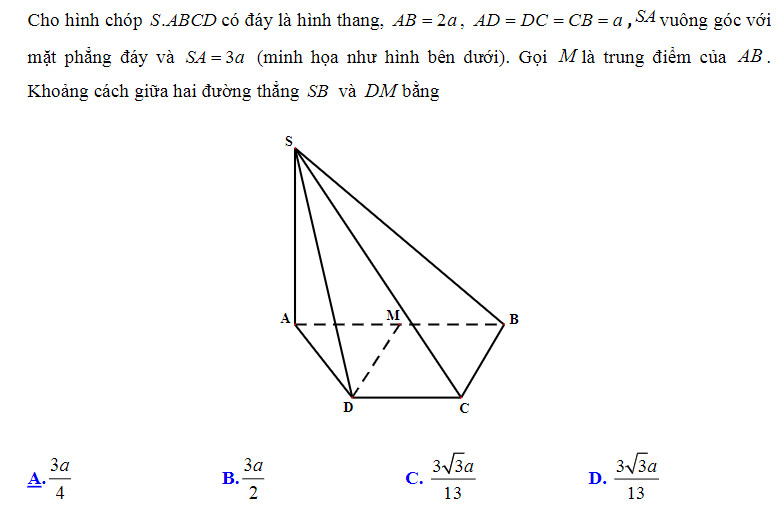
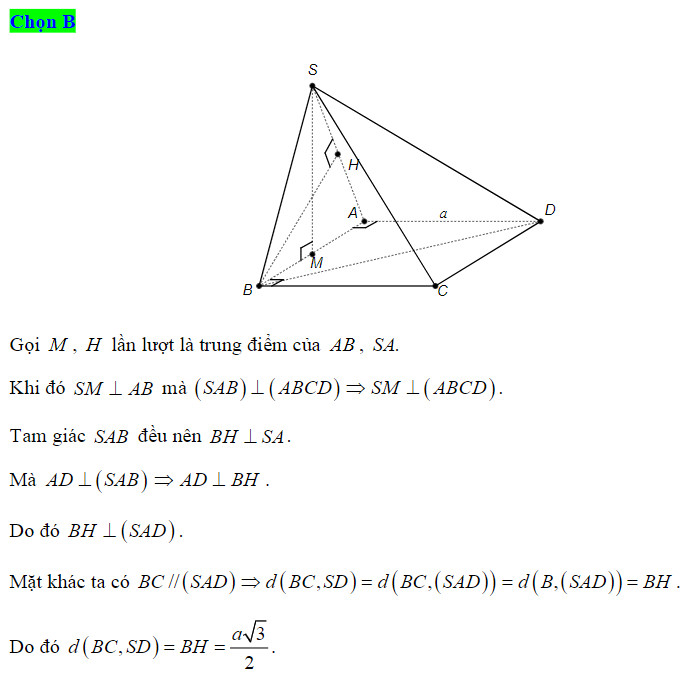
Bài 1:
Giải:
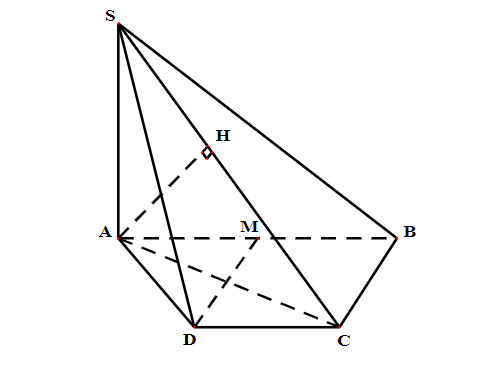
Vì M là trung điểm của AB ⇒ AM = BM = (1/2)AB = a = AD = BC = CD.
Nên tứ giác ADCM và BCDM là hình thoi.
Do
(1)
Xét tam giác ABC có đường trung tuyến vuông tại đỉnh
Trong tam giác vuông SAC, ta dựng AH ⊥ SC.
Xét
Xét thấy tam giác ABC vuông tại C,
Vì tam giác SAC vuông tại A, ta có:
Từ (1) suy ra:
Kết luận:
Bài 2:
Giải:
Bài 3:
Giải:
Bài 4:
Giải:
Bài 5:
Giải:
Bài 6:
Giải:
Bài 7:
Giải:
Bài 8:
Giải:
Bài 9:
Giải:
Bài 10:
Giải:
Bài 11:
Giải:
4. Các Câu Hỏi Thường Gặp (FAQ)
4.1. Làm thế nào để xác định hai đường thẳng có chéo nhau hay không?
Để xác định hai đường thẳng có chéo nhau không, bạn cần kiểm tra xem chúng có đồng phẳng hay không. Nếu chúng không cùng nằm trong một mặt phẳng, chúng chéo nhau.
4.2. Khi nào nên sử dụng phương pháp dựng đoạn vuông góc chung?
Phương pháp này hiệu quả khi hai đường thẳng vuông góc với nhau, giúp việc tìm và dựng đường vuông góc chung trở nên đơn giản.
4.3. Phương pháp tính khoảng cách từ đường thẳng đến mặt phẳng song song áp dụng khi nào?
Phương pháp này phù hợp khi hai đường thẳng chéo nhau nhưng không vuông góc, giúp chuyển bài toán về việc tìm khoảng cách từ một điểm đến một mặt phẳng.
4.4. Tại sao cần chuyển về tính khoảng cách giữa hai mặt phẳng song song?
Việc này giúp đơn giản hóa bài toán khi việc kẻ đường thẳng song song với một trong hai đường thẳng ban đầu gặp khó khăn.
4.5. Có những lưu ý gì khi giải bài tập về khoảng cách giữa hai đường thẳng?
Cần xác định đúng vị trí tương đối của hai đường thẳng, lựa chọn phương pháp phù hợp và thực hiện các phép tính cẩn thận.
4.6. Làm sao để rèn luyện kỹ năng giải bài tập hình học không gian hiệu quả?
Thực hành thường xuyên, làm nhiều dạng bài tập khác nhau và tham khảo các nguồn tài liệu uy tín như tic.edu.vn.
4.7. Kiến thức về khoảng cách giữa hai đường thẳng có ứng dụng gì trong thực tế?
Ứng dụng trong kiến trúc, xây dựng, thiết kế máy móc, đồ họa máy tính, robot học và nhiều lĩnh vực khác.
4.8. Học sinh, sinh viên có thể tìm thêm tài liệu và bài tập ở đâu?
tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, giúp bạn nâng cao kiến thức và kỹ năng.
4.9. Làm thế nào để kết nối với cộng đồng học tập trực tuyến?
Tham gia cộng đồng học tập trực tuyến của tic.edu.vn để trao đổi kiến thức, kinh nghiệm và học hỏi lẫn nhau.
4.10. tic.edu.vn có những công cụ hỗ trợ học tập nào?
tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả như công cụ ghi chú, quản lý thời gian và nhiều tài liệu tham khảo hữu ích.
5. Khám Phá Thế Giới Toán Học Cùng Tic.edu.vn
Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy? Bạn mất nhiều thời gian để tổng hợp thông tin giáo dục từ nhiều nguồn khác nhau? Bạn mong muốn có các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Hãy đến với tic.edu.vn, nơi bạn sẽ tìm thấy:
- Nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt: Từ sách giáo khoa, bài tập, đề thi đến các tài liệu tham khảo chuyên sâu, tic.edu.vn cung cấp cho bạn một kho tàng kiến thức phong phú, đáp ứng mọi nhu cầu học tập.
- Thông tin giáo dục mới nhất và chính xác: tic.edu.vn luôn cập nhật những thông tin mới nhất về các kỳ thi, chương trình học, phương pháp giáo dục và các xu hướng phát triển trong lĩnh vực giáo dục.
- Công cụ hỗ trợ học tập trực tuyến hiệu quả: tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến như công cụ ghi chú, quản lý thời gian, giúp bạn học tập hiệu quả hơn.
- Cộng đồng học tập trực tuyến sôi nổi: Tham gia cộng đồng học tập của tic.edu.vn, bạn sẽ có cơ hội giao lưu, học hỏi và chia sẻ kiến thức với những người cùng chí hướng.
- Cơ hội phát triển kỹ năng mềm và kỹ năng chuyên môn: tic.edu.vn cung cấp các khóa học và tài liệu giúp bạn phát triển kỹ năng mềm như kỹ năng giao tiếp, làm việc nhóm, tư duy sáng tạo và các kỹ năng chuyên môn cần thiết cho sự nghiệp.
Đừng chần chừ nữa, hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!
Thông tin liên hệ:
- Email: [email protected]
- Trang web: tic.edu.vn