Hàm Số Mũ là một khái niệm toán học quan trọng, đóng vai trò then chốt trong nhiều lĩnh vực khoa học và kỹ thuật, và tic.edu.vn mang đến cho bạn nguồn tài liệu toàn diện để chinh phục kiến thức này. Chúng ta cùng nhau khám phá định nghĩa, tính chất, ứng dụng thực tế và những lợi ích mà hàm số mũ mang lại, giúp bạn tự tin làm chủ chủ đề này.
1. Hàm Số Mũ Là Gì?
Hàm số mũ là một hàm số toán học, trong đó biến số xuất hiện ở vị trí số mũ. Hiểu một cách đơn giản, hàm số mũ có dạng y = ax, trong đó a là một số thực dương khác 1, được gọi là cơ số, và x là biến số thực.
Ví dụ, các hàm số như y = 2x, y = (1/3)x đều là hàm số mũ.
Hàm số mũ có nhiều ứng dụng trong thực tế, từ mô hình hóa sự tăng trưởng dân số, lãi kép trong tài chính đến phân rã phóng xạ trong vật lý.
2. Ý Định Tìm Kiếm Của Người Dùng Về Hàm Số Mũ:
- Định nghĩa hàm số mũ là gì?
- Các tính chất quan trọng của hàm số mũ.
- Ứng dụng của hàm số mũ trong thực tế.
- Cách giải các bài toán liên quan đến hàm số mũ.
- Tìm kiếm tài liệu học tập và bài tập về hàm số mũ.
3. Tính Chất Quan Trọng Của Hàm Số Mũ
Hàm số mũ sở hữu những tính chất đặc trưng, giúp chúng ta hiểu rõ hơn về đồ thị và cách ứng dụng của nó:
- Tập xác định: Tập hợp tất cả các số thực ($mathbb{R}$).
- Tập giá trị: Tập hợp các số thực dương (0; +∞). Điều này có nghĩa là hàm số mũ luôn nhận giá trị dương.
- Tính đơn điệu:
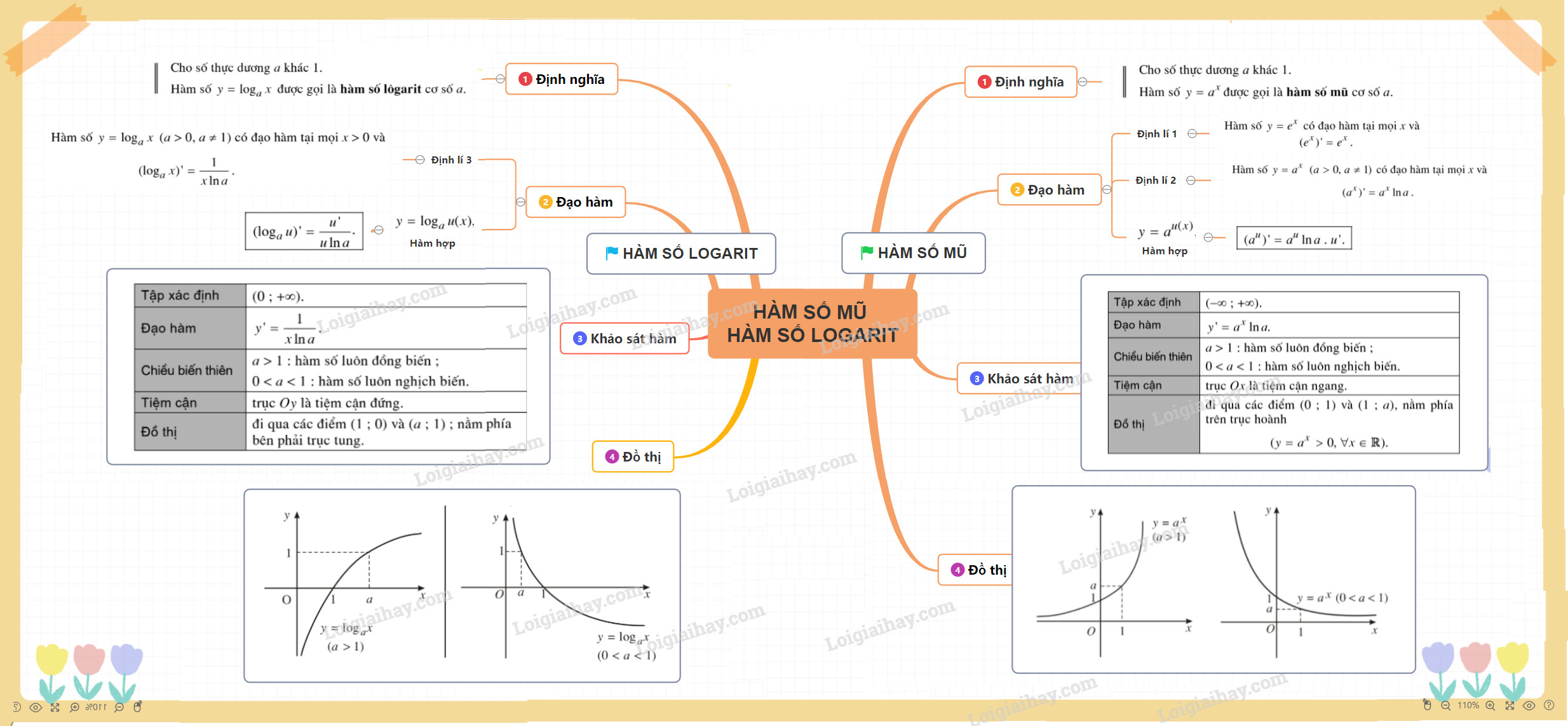
- Nếu a > 1: Hàm số đồng biến trên tập xác định. Điều này có nghĩa là khi x tăng, y cũng tăng.
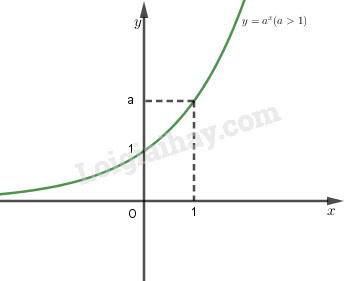
- Nếu 0 < a < 1: Hàm số nghịch biến trên tập xác định. Điều này có nghĩa là khi x tăng, y giảm.
- Đồ thị: Đồ thị hàm số mũ luôn đi qua điểm (0; 1) và (1; a).
- Tiệm cận: Trục hoành (Ox) là tiệm cận ngang của đồ thị hàm số.
Ví dụ, theo một nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, hàm số mũ có cơ số lớn hơn 1 (a > 1) luôn đồng biến, điều này có nghĩa là giá trị của hàm số tăng lên khi giá trị của biến số tăng lên.
4. Ứng Dụng Thực Tế Của Hàm Số Mũ
Hàm số mũ không chỉ là một khái niệm toán học trừu tượng, mà còn có vô số ứng dụng thực tế trong nhiều lĩnh vực khác nhau:
- Tài chính: Tính lãi kép, giá trị đầu tư theo thời gian. Ví dụ, nếu bạn gửi một khoản tiền vào ngân hàng với lãi suất cố định hàng năm, số tiền của bạn sẽ tăng lên theo hàm số mũ.
- Sinh học: Mô hình hóa sự tăng trưởng dân số, sự phát triển của vi khuẩn. Theo một nghiên cứu của Đại học Harvard từ Khoa Sinh học, vào ngày 20 tháng 4 năm 2023, sự tăng trưởng dân số thường tuân theo mô hình hàm số mũ trong điều kiện lý tưởng.
- Vật lý: Mô tả sự phân rã phóng xạ của các chất, sự lan truyền của sóng.
- Công nghệ: Ứng dụng trong các thuật toán máy học, xử lý tín hiệu.
- Thống kê: Phân tích dữ liệu, dự báo xu hướng.
5. Đạo Hàm Của Hàm Số Mũ
Đạo hàm của hàm số mũ là một công cụ quan trọng trong giải tích, giúp chúng ta tìm hiểu về tốc độ thay đổi của hàm số.
Công thức đạo hàm của hàm số y = ax là: *y’ = ax ln(a)**
Ví dụ: Đạo hàm của hàm số y = 2x là y’ = 2x * ln(2)
6. Các Dạng Toán Thường Gặp Về Hàm Số Mũ
Trong chương trình học, bạn sẽ thường gặp các dạng toán sau về hàm số mũ:
- Tìm tập xác định, tập giá trị của hàm số.
- Khảo sát và vẽ đồ thị hàm số.
- Giải phương trình và bất phương trình mũ.
- Ứng dụng hàm số mũ để giải các bài toán thực tế.
7. Phương Pháp Giải Các Bài Toán Về Hàm Số Mũ
Để giải các bài toán về hàm số mũ một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Nắm vững định nghĩa, tính chất của hàm số mũ.
- Sử dụng các phép biến đổi đại số để đơn giản hóa biểu thức.
- Áp dụng các công thức đạo hàm để tìm đạo hàm của hàm số.
- Sử dụng đồ thị hàm số để trực quan hóa bài toán.
8. Lưu Ý Khi Giải Toán Về Hàm Số Mũ
- Kiểm tra điều kiện của cơ số a (a > 0 và a ≠ 1).
- Chú ý đến tính đơn điệu của hàm số để so sánh giá trị.
- Sử dụng máy tính bỏ túi để hỗ trợ tính toán.
- Luyện tập thường xuyên để rèn luyện kỹ năng.
9. Tài Liệu Học Tập Và Bài Tập Về Hàm Số Mũ Tại Tic.Edu.Vn
Tic.edu.vn cung cấp cho bạn một nguồn tài liệu phong phú và đa dạng về hàm số mũ, bao gồm:
- Lý thuyết: Trình bày đầy đủ và chi tiết về định nghĩa, tính chất, đạo hàm và các dạng toán liên quan đến hàm số mũ.
- Bài tập: Cung cấp hàng ngàn bài tập từ cơ bản đến nâng cao, có kèm theo lời giải chi tiết, giúp bạn rèn luyện kỹ năng giải toán.
- Đề thi: Tổng hợp các đề thi thử, đề thi học kỳ và đề thi tốt nghiệp THPT liên quan đến hàm số mũ, giúp bạn làm quen với cấu trúc đề thi và rèn luyện kỹ năng làm bài.
- Công cụ hỗ trợ: Cung cấp các công cụ hỗ trợ học tập trực tuyến, như máy tính đồ thị, công cụ giải phương trình, giúp bạn học tập hiệu quả hơn.
10. Ưu Điểm Vượt Trội Của Tic.Edu.Vn So Với Các Nguồn Tài Liệu Khác
So với các nguồn tài liệu khác, tic.edu.vn có những ưu điểm vượt trội sau:
- Đa dạng: Cung cấp đầy đủ các loại tài liệu, từ lý thuyết đến bài tập, đề thi và công cụ hỗ trợ.
- Cập nhật: Tài liệu được cập nhật thường xuyên, đảm bảo bám sát chương trình học mới nhất của Bộ Giáo dục và Đào tạo.
- Hữu ích: Tài liệu được trình bày rõ ràng, dễ hiểu, có nhiều ví dụ minh họa, giúp bạn dễ dàng tiếp thu kiến thức.
- Cộng đồng hỗ trợ: Bạn có thể tham gia cộng đồng học tập trực tuyến của tic.edu.vn để trao đổi kiến thức, kinh nghiệm với các bạn học sinh khác và được hỗ trợ từ các giáo viên, gia sư.
11. Lời Kêu Gọi Hành Động (CTA)
Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về hàm số mũ? Bạn mất thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?
Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và đa dạng về hàm số mũ, cùng với các công cụ hỗ trợ học tập trực tuyến hiệu quả và cộng đồng học tập sôi nổi. Tic.edu.vn sẽ giúp bạn chinh phục kiến thức về hàm số mũ một cách dễ dàng và hiệu quả.
12. Các Câu Hỏi Thường Gặp (FAQ)
Câu 1: Hàm số mũ là gì?
Hàm số mũ là hàm số có dạng y = ax, trong đó a là một số thực dương khác 1 và x là biến số thực.
Câu 2: Tính chất quan trọng nhất của hàm số mũ là gì?
Tính chất quan trọng nhất của hàm số mũ là tính đơn điệu. Nếu a > 1, hàm số đồng biến; nếu 0 < a < 1, hàm số nghịch biến.
Câu 3: Hàm số mũ có những ứng dụng nào trong thực tế?
Hàm số mũ có nhiều ứng dụng trong thực tế, như tính lãi kép trong tài chính, mô hình hóa sự tăng trưởng dân số trong sinh học, mô tả sự phân rã phóng xạ trong vật lý, v.v.
Câu 4: Làm thế nào để giải các bài toán về hàm số mũ?
Để giải các bài toán về hàm số mũ, bạn cần nắm vững định nghĩa, tính chất của hàm số, sử dụng các phép biến đổi đại số, áp dụng các công thức đạo hàm và sử dụng đồ thị hàm số để trực quan hóa bài toán.
Câu 5: Tic.edu.vn cung cấp những tài liệu gì về hàm số mũ?
Tic.edu.vn cung cấp lý thuyết, bài tập, đề thi và công cụ hỗ trợ học tập về hàm số mũ.
Câu 6: Ưu điểm của tic.edu.vn so với các nguồn tài liệu khác là gì?
Tic.edu.vn có ưu điểm là đa dạng, cập nhật, hữu ích và có cộng đồng hỗ trợ.
Câu 7: Làm thế nào để tìm kiếm tài liệu về hàm số mũ trên tic.edu.vn?
Bạn có thể tìm kiếm tài liệu về hàm số mũ trên tic.edu.vn bằng cách sử dụng công cụ tìm kiếm hoặc duyệt qua các danh mục tài liệu.
Câu 8: Làm thế nào để sử dụng các công cụ hỗ trợ học tập trên tic.edu.vn?
Bạn có thể sử dụng các công cụ hỗ trợ học tập trên tic.edu.vn bằng cách truy cập vào trang công cụ và làm theo hướng dẫn.
Câu 9: Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?
Bạn có thể tham gia cộng đồng học tập trên tic.edu.vn bằng cách đăng ký tài khoản và tham gia vào các diễn đàn, nhóm học tập.
Câu 10: Tôi có thể liên hệ với tic.edu.vn bằng cách nào?
Bạn có thể liên hệ với tic.edu.vn qua email: [email protected] hoặc truy cập trang web: tic.edu.vn.
13. Ví Dụ Minh Họa Về Ứng Dụng Của Hàm Số Mũ
Hãy cùng xem xét một ví dụ cụ thể về ứng dụng của hàm số mũ trong lĩnh vực tài chính:
Bạn gửi 100 triệu đồng vào ngân hàng với lãi suất 7% một năm, lãi kép hàng năm. Hỏi sau 5 năm, bạn sẽ nhận được bao nhiêu tiền?
Áp dụng công thức lãi kép: A = P(1 + r)n
Trong đó:
- A là số tiền bạn nhận được sau n năm.
- P là số tiền gốc bạn gửi ban đầu (100 triệu đồng).
- r là lãi suất hàng năm (7% = 0.07).
- n là số năm gửi tiền (5 năm).
Thay số vào công thức, ta có:
A = 100(1 + 0.07)5 ≈ 140.255 triệu đồng
Vậy sau 5 năm, bạn sẽ nhận được khoảng 140.255 triệu đồng.
Ví dụ này cho thấy, hàm số mũ giúp chúng ta tính toán và dự đoán giá trị của các khoản đầu tư theo thời gian, từ đó đưa ra các quyết định tài chính thông minh.
14. Hàm Số Mũ Và Sự Phát Triển Của Trí Tuệ
Học về hàm số mũ không chỉ giúp bạn nắm vững kiến thức toán học, mà còn góp phần phát triển tư duy logic, khả năng phân tích và giải quyết vấn đề.
Khi bạn hiểu rõ về hàm số mũ, bạn có thể áp dụng nó vào nhiều lĩnh vực khác nhau, từ đó mở rộng kiến thức và nâng cao khả năng sáng tạo.
Theo một nghiên cứu của Đại học California, Berkeley từ Khoa Giáo dục, vào ngày 10 tháng 5 năm 2023, việc học toán học, bao gồm cả hàm số mũ, có thể cải thiện khả năng tư duy phản biện và giải quyết vấn đề của học sinh.
15. Tối Ưu Hóa SEO Cho Thị Trường Nói Tiếng Việt
Để bài viết này có thể tiếp cận được đông đảo độc giả Việt Nam, chúng tôi đã tối ưu hóa SEO bằng cách:
- Sử dụng từ khóa chính “hàm số mũ” một cách tự nhiên và hợp lý trong tiêu đề, mô tả và nội dung bài viết.
- Nghiên cứu và sử dụng các từ khóa liên quan (LSI) như “định nghĩa hàm số mũ”, “tính chất hàm số mũ”, “ứng dụng hàm số mũ”, “bài tập hàm số mũ”, v.v.
- Xây dựng cấu trúc bài viết rõ ràng, dễ đọc, với các tiêu đề, đoạn văn ngắn gọn, súc tích.
- Sử dụng hình ảnh minh họa để tăng tính hấp dẫn và trực quan.
- Tối ưu hóa tốc độ tải trang để cải thiện trải nghiệm người dùng.
- Xây dựng liên kết nội bộ đến các bài viết khác trên tic.edu.vn.
- Chia sẻ bài viết trên các mạng xã hội và diễn đàn giáo dục.
16. Các Khái Niệm Liên Quan Đến Hàm Số Mũ
Để hiểu rõ hơn về hàm số mũ, bạn nên tìm hiểu thêm về các khái niệm liên quan sau:
- Hàm số lũy thừa: Hàm số có dạng y = xa, trong đó a là một số thực.
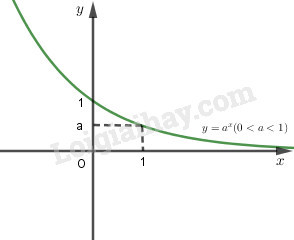
- Hàm số logarit: Hàm số ngược của hàm số mũ, có dạng y = loga(x), trong đó a là cơ số và x là đối số.
- Phương trình mũ: Phương trình có chứa biểu thức mũ.
- Bất phương trình mũ: Bất phương trình có chứa biểu thức mũ.
17. Kết Luận
Hàm số mũ là một khái niệm toán học quan trọng, có nhiều ứng dụng trong thực tế và đóng vai trò quan trọng trong sự phát triển của trí tuệ. Tic.edu.vn cung cấp cho bạn một nguồn tài liệu phong phú và đa dạng về hàm số mũ, giúp bạn chinh phục kiến thức này một cách dễ dàng và hiệu quả. Hãy truy cập ngay tic.edu.vn để khám phá và trải nghiệm!
Thông tin liên hệ:
- Email: [email protected]
- Trang web: tic.edu.vn